A Historical Perspectives of Soliton in Science and Technology

Abstract

A soliton is a localised wave packet that is highly stable, nonlinear, self-reinforcing, and propagates freely at a constant speed. It keeps its shape even after colliding with other similar localised wave packets. The medium\'s exceptional stability can be attributed to its balanced elimination of dispersive and nonlinear effects. Many systems exhibit dispersive effects, in which the wave frequency controls the wave\'s speed of propagation. It was later demonstrated that soliton solutions provide stable solutions for a wide variety of dispersive partial differential equations that are weakly nonlinear and describe physical systems. Solitons are preferred for high-speed, long-distance transmissions because of their self-restoring characteristic.Transmission speeds over longer distances are currently approaching 40 Gbit/sec, meaning that the strain on networks is rapidly approaching a critical threshold.

Introduction

I. INTRODUCTION

A generally agreed definition of soliton is difficult to come up with. Drazin & Johnson provide solitons three features (1989, p. 15) [1]. They possess three qualities: they can interact with other solitons, they are confined within a region, and they have a permanent form. They also survive collisions intact, with the exception of a phase shift.Although there are more formal formulations available, they require a great deal of mathematics. Moreover, a few of scientists label occurrences that don't meet these three requirements as soliton phenomena (for example, even though "light bullets" lose energy during interaction, they are occasionally referred to as solitons in nonlinear optics).[2]Dispersion and nonlinearity can interact to produce both permanent and localised wave patterns. Imagine a pulse of light travelling through glass. We could suppose that this pulse is composed of multiple light frequencies. The dispersion of glass causes these distinct frequencies to travel through it at different speeds, which causes the pulse's shape to change over time. However, there is also the nonlinear Kerr effect, where a material's refractive index at a given frequency is determined by the amplitude or brightness of the light. A properly formed pulse has a stable shape throughout time because the Kerr effect precisely cancels out the dispersion effect. As such, the pulse is a soliton [3]. Numerous models that are completely solvable are solved by solitons, including the coupled nonlinear Schrödinger equation, the Korteweg–de Vries equation, the sine-Gordon equation, and the nonlinear Schrödinger equation. The integrability of the field equations—which is typically accomplished via the inverse scattering transform—is responsible for the stability of the soliton solutions. The mathematical theory of these equations is a broad and active field of mathematical study [3].

A train of solitons follows a wavefront in some "undular" tidal bore occurrences that are found in a few rivers, including the River Severn. More solitons are produced as underwater internal waves driven by the topography of the seafloor spread out along the oceanic pycnocline. There are further atmospheric solitons. As an illustration, consider the morning glory cloud in the Gulf of Carpentaria, which is produced by enormous linear roll clouds that are brought about by pressure solitons passing over a layer of temperature inversion. In the recently constructed, but not widely accepted, soliton model of neuroscience, pressure solitons are used to explain the signal conduction within neurons [3]. A topological soliton, often called a topological defect, is any solution of a system of partial differential equations that is persistent against decay to the "trivial solution". Topological restrictions, not the integrability of the field equations, are the source of soliton stability. Constraints are almost always present because the differential equations must adhere to a set of boundary conditions and maintain the nontrivial homotopy group of the boundary. As a result, homotopy classes can be used to group differential equation solutions [3].

Specifically, soliton transmission in optical fibres counteracts two primary types of pulse degradation in order to improve the quality of data transmission. One type of degradation is the dispersion that happens when pulses travel over long fibre stretches. The other is the nonlinear effects that arise from signals interacting in a power-dependent way with the fibre and with each other.

Generally, the combined effect of the two effects makes the situation worse; but, for certain optical pulse forms and powers, the effects can cancel each other out, at least to a first-order approximation. Soliton is the term used to describe these types of pulses.The inherent durability of solitons for long-distance high-speed gearboxes is one of their main advantages. Over long fibre lengths, soliton can be made intrinsically stable despite soliton attenuation. This offers a way to stop dispersion and nonlinear effects from deteriorating signal quality, which is a major problem at 10 Gbit/s and gets worse at higher transmission speeds. Due to these features, scientists are developing soliton systems for long-haul 10-Gbit/s and upcoming 40-Gbit/s systems [4].

II. LITERATURE REVIEW

John Scott Russell (1808–1882) initially reported the soliton phenomenon in 1834 when he saw a lone wave in Scotland's Union Canal. He called it the "Wave of Translation" after he successfully replicated the phenomenon in a wave tank. The Korteweg–de Vries equation, which represents waves similar to those seen by Russell, has localised, strongly stable propagating solutions. Zabusky and Kruskal first used the name soliton to describe these solutions. With the "on" suffix, which was originally used to refer to particles like hadrons, baryons, and electrons and reflected their observed particle-like activity, the word was intended to describe the solitary nature of the waves.[3]. The soliton phenomena was first documented in 1834 by John Scott Russell (1808–1882), who observed a single wave in Scotland's Union Canal. After he successfully duplicated the event in a wave tank, he dubbed it the "Wave of Translation". There are locally confined, strongly stable propagating solutions to the Korteweg–de Vries equation, which describes waves that resemble those observed by Russell. It was Zabusky and Kruskal who originally dubbed these solutions soliton. The word was meant to describe the solitary nature of the waves, with the suffix "on" reflecting its original usage to denote to particles such as hadrons, baryons, and electrons and reflecting their observed particle-like activity.[3].

The earliest known observation of a lone wave was made by a young engineer named John Scott Russell, who was hired for a summer project in 1834 to investigate methods to improve the designs for barges designed to traverse canals, notably the Union Canal in Edinburgh, Scotland. One day in August, the tow rope that was securing the mules to the barge broke, causing it to stop suddenly. Nevertheless, the water mass ahead of the barge's blunt prow rolled forward quickly, taking the shape of a sizable isolated elevation—a rounded, smooth, and well-defined mound of water—and continued down the canal without changing shape or pace. Russell (1844). After conducting further research into this coincidental finding, Russell rode up to the Wave of Translation and overtook it as it continued to roll at a speed of around eight or nine miles per hour, maintaining its original dimensions of about thirty feet by one foot to one and a half. He then used a wave tank in carefully controlled laboratory experiments, and in 1844 he reported the results (Russell, 1844). He provided four examples: He observed hyperbolic secant structure in single waves.If the starting water mass is sufficiently enormous, it can produce two or more waves that break apart gradually and become nearly solitary.Waves can flow past one another "without change of any kind" when they are isolated. n a shallow water channel of height h , a solitary wave of amplitude A travels at a speed of [g(A+h)]1/2 , where g is the gravitational acceleration. It is a nonlinear phenomena where waves with greater amplitudes travel quicker than those with smaller amplitudes.

Diederick Korteweg, a Dutch physicist, and his student Gustav de Vries (KdV) (de Vries, 1895) (Scott, 2005) devised a nonlinear partial differential equation (PDE) that is currently named after them in 1895. Korteweg and de Vries suggest that the KdV equation (1) could account for Russell's experiments. Equation (1) shows that the dispersive term, which allows waves of different wavelengths to travel at different velocities, the amplitude effect, and a nonlinear component add together to determine the rate of change of the wave's height over time. Korteweg and de Vries found a periodic solution in addition to a solitary-wave solution that matched the wave that Russell had pursued. These solutions resulted from a trade-off between dispersion and nonlinearity. Up until 1965, when Norman Zabusky and Martin Kruskal published their numerical solutions to the KdV equation (and invented the phrase "soliton"), mathematicians, physicists, and engineers studying water waves ignored their work and Russell's discoveries (Zabusky, 1965). From (1), Kruskal developed a continuous description of the oscillations of unidirectional waves propagating on the cubic, Fermi–Pasta–Ulam (FPU) nonlinear lattice (Fermi, 1955; Porter, 2009b; Weissert, 1997). In parallel, Morikazu Toda created history when he became the first person to detect a soliton in what is now known as the Toda lattice, a discrete, integrable system (Toda, 1967).[5]

Gary Deem, Zabusky, and Kruskal (1965) made films showing interacting solitary waves in an FPU lattice, the KdV equation, and a modified KdV equation; see the discussion in the review paper (Zabusky, 1984). Using the KdV equation, we demonstrate the dynamics of solitons in Figure 1's space-time diagram. When Robert Miura realised the significance of this discovery, he found a precise transition between this modified KdV equation and equation (1) (Miura, 1976). When Clifford Gardner, John Greene, Martin Kruskal, and Robert Miura employed the inverse scattering approach to resolve the initial-value problem of the KdV equation in 1967 (Miura, 1968; Gardner, 1967; Gardner, 1974), this generated interest in the mathematical study of solitons. This led to the development of an appropriate notion of integrability for continuum frameworks. In 1972, Alexei Borisovich Shabat and Vladimir Zakharov extended the inverse scattering method by proving the existence of soliton solutions and the integrability of the nonlinear Schrödinger (NLS) problem. The sine-Gordon equation was one of several nonlinear PDEs that Mark Ablowitz, David Kaup, Alan Newell, and Harvey Segur proved to have soliton solutions for in 1973. This equation was already known to be integrable due to Albert Backlünd's 19th century investigations of surfaces with constant negative Gaussian curvature. Other researchers have since developed related soliton solutions and derived different integrable PDEs (in one and multiple spatial dimensions). A more complex definition of a "soliton" in several spatial dimensions is required, as the Kadomtsev–Petviashvili (KP) equation illustrates. Asymptotic analysis, variational approximations, and/or perturbative techniques are typically used in analytical approaches for investigating solitary waves in nonintegrable equations (Kivshar, 1989). (Scott, 2005) In optics, the coupled mode equations of the fibre Bragg grating are a prominent example of a nonintegrable system with precise solutions for isolated solitary waves. The study of solitons and solitary waves is currently one of the most active areas in mathematics and physics (Scott, 2005). It has impacted many fields, including pure mathematics and experimental science. This has led to important discoveries in nonlinear dynamics, biology, optics, supersymmetry, and integrable systems, among other domains. Later in this piece, we shall discuss some of the varieties and applications of solitary waves. [5]

III. MATHEMATICAL EQUATIONS OF  SOLITON

A non-linear evolution equation that is solved at each instant and localised in a bounded domain of space, with the domain's size being bounded in time and its centre of motion being understood as the motion of a particle. The Korteweg–de Vries equation's soliton solution [6].

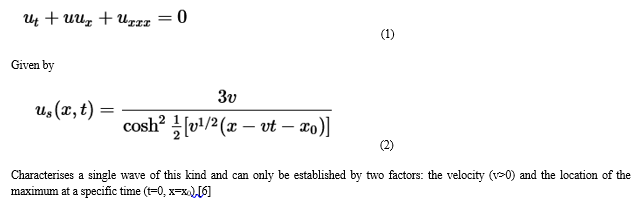
Conclusion

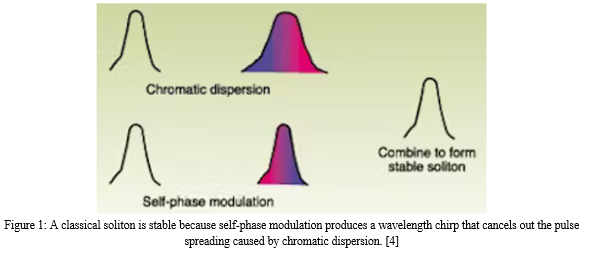
In a non-linear dispersive medium, solitons light pulses can propagate over very long distances without broadening. As a result, they have drawn a lot of interest from the communications sector. Two effects that can balance each other out under the appropriate conditions are the reason solitons work in optical fibres. Chromatic dispersion is one of them; it happens when pulses with different wavelengths spread out as they move through an optical fibre. The alternative is referred to as self-phase modulation, or SPM, and it operates across a larger range of pulse spectrum wavelengths. Once the pulse finds equilibrium in the fibre, dispersion and SPM can counterbalance each other, allowing the pulse to keep its shape or dispersion. The pulse may potentially more severely expand or compress as a result of SPM. Conversely, attenuation reduces the pulse\'s strength and makes it more difficult for it to maintain its shape over the fibre span. Optical amplifiers have been constructed to balance attenuation and preserve pulse shapes. [9, 10].

References

[1] Drazin, P. G.; Johnson, R. S. (1989). Solitons: an introduction (2nd ed.). Cambridge University Press. ISBN 978-0-521-33655-0. [2] https://www.sfu.ca/~renns/lbullets.html#bullets [3] https://en.wikipedia.org/wiki/Soliton#cite_note-2 [4] https://www.laserfocusworld.com/fiber-optics/article/16556409/solitons-balance-signals-for-transmission [5] http://www.scholarpedia.org/article/Soliton [6] https://encyclopediaofmath.o rg/wiki/Soliton [7] G. P. Agrawal, Nonlinear Fiber Optics, (Academic Press, 2007) [8] https://wp.optics.arizona.edu/kkieu/wp-content/uploads/sites/29/2019/04/Solitons-in-optical-fibers-04-05-19.pdf [9] https://www.lightwaveonline.com/optical-tech/transport/article/16647155/future-of-solitons [10] Lightwave, \"Handling Special Effects: Nonlinearity, Chromatic Dispersion, and Soliton Waves,\" July 2000, page 84.)

Copyright

Copyright © 2024 Muhammad Arif Bin Jalil. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.