A Review of Various Optimization Strategies for Handling Optimal PMU Placement Problems

Abstract

The Phasor Measurement Unit (PMU) is the most fundamental power system technology that is utilized to protect, monitor, and control power networks. It not only allows real-time, synchronized voltage measurements on the buses but also the current phasor of lines connected to the buses where these PMUs are placed. The positioning of PMUs at each bus node is unnecessary and is restricted by the installation\'s high cost and complexity. As a result, the fundamental goal of Optimal PMU placement (OPP) is reducing the total no. of PMUs along with maximum observability, while simultaneously considering measurement redundancy. There are several methods for fixing this problem, and they fall into two categories: Metaheuristic methods and mathematical approaches. This study examines a variety of optimization strategies for handling OPP problems.

Introduction

I. INTRODUCTION

Due to technological breakthroughs and rising living standards worldwide, there has been an increase in the need for power in recent years. In such a situation, a system that not only monitors but also precisely measures instruments is required for proper and steady power system function. This duty was priorly accomplished by SCADA, which relies on unsynchronized measurements to estimate system states [1]. The voltage magnitudes of buses, as well as their real and reactive powers, are provided by SCADA, although measurements based on SCADA are delayed due to their slow duty cycle. Furthermore, traditional measurement instruments do not offer bus voltage angles. The WAMPAC technology is utilized to solve these restrictions in the SCADA and to measure the angles of the bus [2] [3]. “A. G. Phadke et al. (2005) the main components of this system are Phasor Measurement Units (PMUs), which offer real-time and synchronized voltage as well as current phasor measurement. Synchronized data is collected when voltage and current signals get sampled along with the timing signals from the GPS (Global Positioning System) satellite at the same time [4] [5]”. PMUs directly calculate the voltage phasor data of all the buses on which they are located, even the current phasor data of the lines that intersect that bus. Unfortunately, the cost of PMUs and their communication services are uneconomical, so it’s impractical to put these units on all of the buses.

“Cherukuri Murthy et al. (2016) PMU accumulates the analog waveform as input data i.e. current and voltage signals from the current transformer (CT) and potential transformer (PT) respectively and then passes to the anti-aliasing filter which is used to avoid an aliasing error. Afterward, these signals are forwarded to the A/D converter which samples the analog voltage and current signals using a sampling clock that is in phase synchronization with the GPS receiver. The central processing unit (CPU) receives the transformed digital signals, processes them as per the algorithm, and outputs the magnitude and phase values of the primary input signal [6]”. Figure 1.1 depicts the acknowledged process quite clearly.

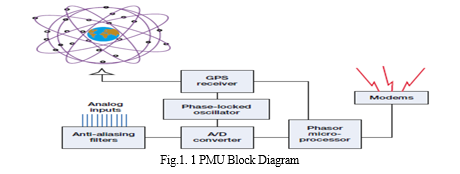
II. OPTIMAL PMU PLACEMENT PROBLEM(OPP)

To place no. of PMUs optimally for observing the whole power network thoroughly, an ideal methodology is necessary. Several approaches are developed for solving the Optimal PMUs Placement (OPP) problem. These techniques are usually classified into 2 classes: conventional and metaheuristic. To tackle OPP, traditional techniques such as Linear Programming are offered. “Heuristic and Metaheuristic optimization methodologies such as Simulated Annealing, Spanning Tree, Particle swarm optimization, Cat Swarm Optimization, Ant Colony Optimization, and many more algorithms are mentioned [7] that overcome issues such as difficulties to obtain local minima and handle constraints in conventional techniques”. This study presents a review of research and studies on traditional and advanced heuristic and metaheuristic optimization strategies for solving the OPP problem i.e., placing PMUs optimally in a power system.

III. MATHEMATICAL PROGRAMMING METHODS

Integer Programming (IP), often known as mathematical programming, is one of the most widely used approaches for numerical programming [7]. This approach has been used to resolve issues involving integer design components. Based on the variety of objective functions and constraints, which may be linear or quadratic, integer programming is divided into integer linear programming (ILP) and integer quadratic programming (IQP).

A. Integer Linear Programming (ILP)

Reference [8] presents a technique for reducing the no. of PMUs strategically placed, resulting in the elimination of criticality in power network measurement. Traditional measurements are included in the approach during PMU placement. Furthermore, when a specific level of redundancy is required, the method is proven to have the same formulation. Then, by extending the placement problem, typical conventional measurement was integrated. If a preferred amount of general redundancy is taken into account, the same algorithm can be used to locate the optimum positions. The identification of bad data improves as the redundancy level rises.

“In reference [9] C.Rakpenthai (2007) introduced a modern algorithm for placing the no. of PMUs optimally observe the entire system in case of any contingency. The proposed algorithm works in 4 stages, with the first stage determining the essential measurement for an entirely known state. It then selects duplicate measurement sets in case of any contingencies in the next stage. To select the Suitable measurement location, both stages use the least condition no. in the normalized measurement matrix. Furthermore, using the binary integer programming technique, the least redundant measurement set is selected out of all accumulated measurements.” Finally, these measurements, both important and minimally redundant, are organized for optimal PMU placement. The heuristic method is utilized for this.

“Bei Gou proposed a universal formulation in ref. [10], for optimally placing PMU, which is required for entire system observability considering and not considering zero injection buses. In [11], he introduced the PMU placement model of ILP”.

ILP is suggested to do the multistage placement of PMUs in Ref. [12]. Constraints on ZIBs are expressed as linear constraints. “The OPP problems have various results, two best ones which are been proposed:  The number of times a bus is seen by a set of PMUs is known as the bus observability index (BOI), whereas the system observability redundancy index (SORI) is calculated as the total of all the BOIs at each bus location [12]. The best set for PMU placement is the one with the highest SORI. The outcomes of the proposed technique are shown in Tables 3.1.1 and 3.1.2.

Table 3.1.1- Minimum no. of PMUs while excluding and including ZIBs

Table 3.1.2- Comparing SORI while excluding and including ZIBs (Initial SORI - Final SORI)

“N.H. Abbasy (2009) [13] proposes a unified technique for concluding the OPP problem as well as making the entire system completely observable. Under standard measurements with either single or several PMU losses contingency, the suggested method considers a choice strategy for the best PMU allocation. Placement problem as BILP (Binary Integer Linear Programming) is formulated by the branch–bus model of this system.”

To estimate the optimum number of PMUs, reference [14] offered ILP with a rapid and new practical model. Line outages and measurement losses are examples of power system contingency conditions. Because various situations can be handled independently or all at once in the power system, the suggested model is more flexible than the existing model. In addition, the model includes measurement concerns, such as power network communication constraints. This strategy has a key benefit, in that it provides a local optimum solution for large-scale power systems in a short amount of time. The outcomes of the technique are shown in Tables 3.1.3 and 3.1.4.

Table 3.1.3- Characteristics of IEEE standard test systems

Table 3.1.4- Minimum no. of PMUs for the IEEE test systems in a different state

“In ref. [15], a Binary Integer Linear Programming (BILP) approach for the entire observability of a power system along with the no. of PMUs placed optimally is shown, as well as a strategy to maximize redundancy not only under normal conditions but also in the fault conditions like PMU failure or line outage”. OPP issue is expressed as a binary integer problem with linear variables constraints. In the power system, the suggested method included the zero-injection bus effect. This method was put to the test on both IEEE standards and wide-scale systems, results are mentioned in Table 3.1.5.

Table 3.1.5- No. of PMUs for observability & SORI

B. Integer Quadratic Programming (IQP)

The connectivity matrix represents network topology and is used to describe the OPP problem. The optimization of the quadratic objective function can be done by including both linear constraints as well as the variable integer value [7]. This procedure going to help in optimizing the number of PMUs by providing complete observability both in normal conditions as well as during an outage situation.

The system is topologically observable using the optimum PMU placing strategy discussed in [16]. IQP technique minimizes the no. of PMUs along with keeping the power system completely observable under the normal condition as shown in Table 3.2.1 and the time required by the CPU to find the optimal PMU locations for various bus systems is mentioned in Table 3.2.2. This strategy also maximizes the system's measurement redundancy.

Table 3.2.1- Minimum no. of PMUs for observability of the entire system under normal conditions

Table 3.2.2- Computational time needed to find the optimal PMU sites

IV. HEURISTIC AND META-HEURISTIC METHODS

A. Simulated Annealing (SA)

Simulated Annealing (SA) is a metaheuristic inherited probabilistic technique. Its major goal is to obtain a roughly reasonable solution independent of the optimal solution for a certain period. This method is generally utilized for discrete search areas. The goal is to discover a fine enough solution other than the most feasible answer in a certain period.

Based on the incomplete observability of the system, the SA approach proposed in [4] suggests a strategy or optimum placement of PMU. First, it makes the system observable and determines the no. of PMUs required by considering the spanning trees of the system graph. This effect of an innovative concept called "depth of unobservability" on the no. of PMUs placed is then presented. This approach also produces appropriate solutions for the PMU placement issue with a communication restriction.

SA was used in [17] to maximize the measurement's redundancy. Moreover, the impact of zero injection bus on system visibility is considered to lessen the no. of installed PMUs without having a significant effect on complete observability. To verify the consistency, efficiency, and effectiveness of the technique, several IEEE standard-bus systems have been examined. Another study [18] uses a multistage SA technique to determine the ideal location for combining PMUs and conventional measurement units. This approach can discover the optimum locations more quickly than other algorithms based on uphill motions across multiple phases, which enables it to arrive at the best solution. It is quicker than other standard SA methods.

B. Genetic Algorithm(GA)

One of the most popular heuristic algorithms is the genetic algorithm (GA), an adaptive search method that can replicate the process of natural evolution to discover the solution [7].

In ref [19] a non-dominated sorting evolutionary algorithm is mentioned that addresses the issue of placing the PMUs optimally along with other objectives, namely reducing the no. of PMUs while optimizing measurement redundancy. The Pareto optimum solutions are obtained using this optimization method. To achieve an individual solution, the proposed technique first employs graph theory and then employs a basic GA procedure. As a result, the Non-dominant Sorting Genetic Algorithm is used to determine the most desirable solution, from which the decision-maker can be chosen (NSGA). The primary aspect of NSGA is providing the best Pareto-optimal solution instead of just a particular solution for multi-objective optimization problems and having a vast search space. Phasor Measurement Units are optimally installed using the Genetic Algorithm in ref. [20] so that the location of the fault in the associated network can be detected. This is categorized into two: the first involves obtaining a small no. of PMUs and placing them in the network, and the second involves detecting the location of the defect using the values collected by the placed PMUs. The method is not only just cost-effective but can also be used on any network that is connected. In ref. [21] genetic algorithm is considering complete power system observability as a mono objective while optimally placing the PMUs. OPP is accomplished in both normal and contingency situations utilizing a genetic algorithm with measurement redundancy and observability evaluation [22].

C. Spanning tree search

In Ref.[23], the spanning tree method and the tree search algorithm were used to improve the OPP problem's solution by taking into account the least channel and multichannel PMUs for optimal observability, also known as spanning tree search. The goal of this study is to investigate how observability depth affects the total number of installed PMUs in the smart grid. The spanning tree method was used to create electricity grid graphs, and the best location for PMUs was found using the tree search method. The same method was also enhanced to identify PMU channels with the least number. This method was evaluated on IEEE standard bus systems in a MATLAB environment to accomplish the objective of the problem.

D. Pollination algorithm

For solving the OPP issue, Ref. [24] offers a unique method termed the flower pollination algorithm (FPA). The pollination process of flowering plants inspired the FPA. With encouraging findings, FPA is now upgraded for various other optimizations. To provide full observability with maximum measurement redundancy at system buses, this problem tries to limit the number of PMUs used. The standard IEEE bus test systems have all been utilized to validate this method. The suggested method's results are compared to those achieved by various conventional optimization methods in Table 4.4.1.

Table 4.4.1- Comparing optimal PMUs placement results of different algorithms

E. Tabu Search (TS)

“This algorithm [25] is a local search metaheuristic technique. By tracing and guiding the search, this approach is utilized to solve problems involving combination optimization.”

The OPP problem is formulated with great accuracy and minimal processing cost using the proposed algorithm. Using a quick observability analysis method, the network's full observability is ensured. As a result, as compared to conventional observability analysis, this method provides faster and more accurate results. TS consist of an augments incidence matrix that manipulates an integer number of state estimate models to fast and easily obtain network observability [25].

F. Best-first search algorithm

The best-first search (BFS) algorithm is utilized in Ref. [26] to attain the OPP with complete observability. A pruning strategy was used to cut down on the overall number of measurement devices already determined by BFS as well as the measurement redundancy of systems created by BFS.

In an IEEE test system, such as the IEEE 14, 30, and 246-bus systems, the aforementioned tactic is shown in operation. After excluding all the radial buses from every PMU placing site it is well known that the amount of PMUs needed for complete observability of the entire system is now reduced. In Table 4.6.1 comparison of the results demonstrates that this technique is significantly more precise than other techniques, such as ILP.

Table 4.6.1- Comparing results of the proposed method with the ILP method

G. Teaching–learning-based optimization technique

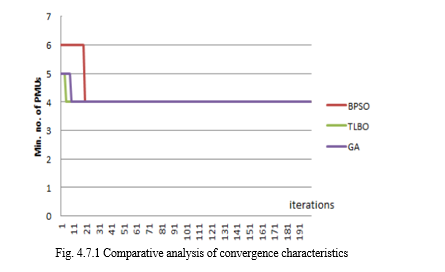
 In Ref. [27] this method is utilized for OPP problems with and without involving ZIBs. This algorithm produces results that are distinct from those of other optimization approaches like GA and BPSO, and it is more effective overall. Moreover, the need for several constraint settings in GA and BPSO reduces the procedure's effectiveness. The teaching-learning-based optimization (TLBO) method, on the other hand, doesn't require a lot of adjustments to its settings and variables. The optimal number of PMUs without ZIB resulting from this method is compared to already existing techniques in the following Table 4.7.1. As can be seen in Figure 4.7.1, the suggested TLBO strategy is therefore easier to implement and converges more quickly than existing approaches.

Table 4.7.1: -Optimal number of PMUs without ZIB

H. Exhaustive Search (ES)

ES is an analytical approach & algorithmic pattern that considers all possible solution candidates and determines whether or not every candidate satisfies the problem statement. The approach is referred to as exhaustive since it guarantees to deliver all accessible states before terminating with a unit failure.

To achieve OPP in Ref. [28], ES is carried out utilizing the ILP. The suggested method included the ZIB. While observing the entire network, the single-line contingencies are even considered. Since the method requires less computing, therefore global optima can be obtained over a very short duration.

For approximate optimal PMU placement, a sophisticated technique known as LEA (Limited Exhaustive Approach) is utilized, which is declared from a complete examination of the power network system. LEA maintains the advantages of ES, which is extremely reliable, preventing it to stuck at local optima. It even reduces the search space, making it a lot quicker than ES [29]. The ES technique is used to perform OPP, with ZIB taken into account [30]. For the OPP problem, [31] proposes an upgraded optimized form of ES called reduced ES. In comparison to ES, it minimizes the search space and the no. of computations required while considering the presence of PMU outage and ZIB. The suggested algorithm out performs ILP and ES in terms of results i.e. mentioned in Tables 4.8.1 & 4.8.2.

Table 4.8.1-OPP minimum PMU count

Table 4.8.2-Runtime

I. Particle Swarm Optimization (PSO)

PSO is a population-based probabilistic optimization technique that was established according to the social activities of flocking (behavior shown by a group of birds flying). 

“In Ref. [32] an updated discrete binary PSO (BPSO) is being used for placing PMUs optimally to solve OPP issue and even for acquiring maximum measurement redundancy at every bus in the power network system. “On a variety of standard IEEE bus systems, this technique has been successfully utilized. This method has been applied in a substantial portion of the Brazilian power system to further test its viability.

The method offers the advantages of simplicity, quickly optimizing adjustment, vast network scalability, and multiple solutions possibilities. Local optima are generated by the algorithm, and by improving the optimization dimensions such as the no. of particles, the algorithm runs and iterations their quality can be upgraded.

OPP is carried out in [33] utilizing an updated PSO technique to estimate the state of the power network system. The full observability of the network provided by the proposed technique is also checked using numerical analysis. The suggested method's results are compared to those achieved by existing optimization methods in Table 4.9.1.

Table 4.9.1- Comparing no. of PMUs stated by the proposed method and existing methods

A hybrid algorithm can offer a better solution since several methods can boost the OPP problem's feasibility in a practical situation. To solve the optimization issue and achieve maximum observability in a power system, the exponential binary PSO (EBPSO) technique has been proposed in Ref. [34].The proposed algorithm's solution potential is improved by using a non-linear inertia-weight coefficient. Two mathematical formulae are utilized to enhance the particle's position to include prior positions. For rapid and reliable convergence, two-stage filtering is used, and a single mutation operation is used conditionally to avoid stagnation. Together with the typical operational scenario, zero injection buses, single-PMU outages, and various practical scenarios are taken into account. A sigmoid function is used in the suggested method to dynamically upgrade the location of each element in the binary procedure.

J. Ant colony optimization (ACO)

ACO is a stochastic optimization technique that uses graphs to find the finest places for the installment of PMUs. It functions similarly to an ant in an ant colony.

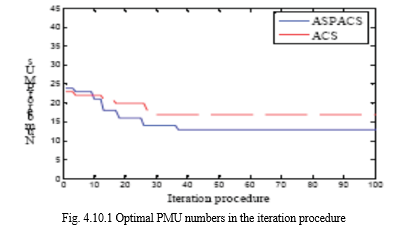
The ACO method is composed to answer the OPP issue of making the total power network observable [35]. As it is not necessary to calculate the transition probability every time while selecting the target site, the ACS increases calculation efficiency. It got the potential to exhibit stagnation behavior and gets trapped in local minima. To enhance the ACS in two ways, an Adaptive Stochastic Perturbing ant Colony System (ASPACS) is proposed in this [35]. To improve the algorithm's ability to avoid stagnation behavior and speed up convergence, this method adds a mechanism for adaptively modifying the pheromone trail persistence coefficient as well as stochastic perturbing. The ASPACS is better than the ACS in terms of convergence speed and optimizing the required no. of PMUs for full observability of the system, results of a 46-bus system PMU placement problem are shown in figure 4.10.1.

K. Cat Swarm Optimization Algorithm (CSO)

CSO is a transmutative strategy that is motivated by the cat’s actions and even be applied to find solutions to various optimization issues. This technique has motivated many researchers in a short period and since then began to be used in a variety of areas. The cat swarm optimization (CSO) technique is also used to solve various power system challenges, one of which is determining the optimal location for distributed generators [36].

The BPSO has resulted in the proposal of a novel technique BCSO, which is an upgraded version of the above-mentioned CSO. The position vector is one of the primary differences that distinguish BCSO from CSO. The various combinations of zeros and ones in BCSO define the position vector. There are 2 stages in BCSO: Seeking and Tracing Mode. BCSO is presented in ref.[37] for the placement of PMUs optimally and for making the system fully observable. This research also compares the minimal no. of PMUs needed for making IEEE standard bus systems observable using various existing optimization strategies.

L. Binary Grey Wolf Optimization (BGWO)

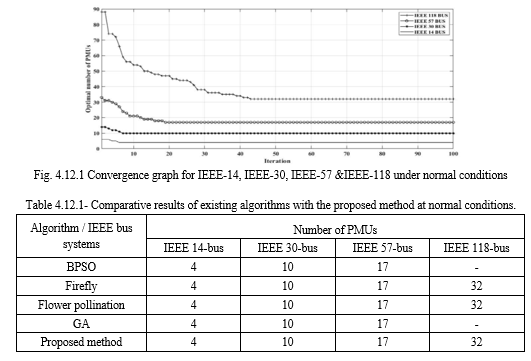
GWO is a recently developed meta-heuristic algorithm based on grey wolf hunting behavior. A novel binary variant of the Grey Wolf Optimization technique (BGWO) is mentioned in this study [38] to handle the problem regarding optimal PMU placement as the results are limited to binary values (0,1). This novel method is not only feasible to implement but also tends to be the finest optimal solution. The BGWO technique is presented to reduce PMU numbers while increasing measurement redundancy (MR), considering the effect of ZIBs, single PMU failure, and channel restrictions. Four IEEE standard systems are used to validate this approach as demonstrated in figure 4.12.1. To demonstrate the superiority and efficacy of the suggested technique, it is compared to other heuristic methods as shown in Table 4.12.1.

Conclusion

Several techniques have been executed to investigate and obtain the preferred solution for the optimal positions for the placement of PMUs. To discover the optimal placement of PMUs (OPP) in power system networks various works have been performed over the years. This paper reviewed the existing solutions for optimally placing PMUs which are categorized into two major categories: conventional mathematical methods and a heuristic algorithm. A review of various optimization approaches presented in this work to alleviate the Optimal PMU Placement problem (OPP) will serve as a guide and aid in the discovery of future optimization criterion trends.

References

[1] M. A. Rahman, A. H. M. Jakaria, and E. Al-Shaer, “Formal Analysis for Dependable Supervisory Control and Data Acquisition in Smart Grids,” in 2016 46th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), IEEE, Jun. 2016, pp. 263–274. doi: 10.1109/DSN.2016.32. [2] Jiaping Liao and Cheng He, “Wide-area monitoring protection and control of future power system networks,” in 2014 IEEE Workshop on Advanced Research and Technology in Industry Applications (WARTIA), IEEE, Sep. 2014, pp. 903–905. doi: 10.1109/WARTIA.2014.6976419. [3] N. R. Chaudhuri, “Wide-Area Monitoring and Control of Smart Energy Cyber-Physical Systems (CPS),” in Smart Cities, Hoboken, NJ, USA: John Wiley & Sons, Inc., 2017, pp. 155–180. doi: 10.1002/9781119226444.ch6. [4] R. F. Nuqui and A. G. Phadke, “Phasor Measurement Unit Placement Techniques for Complete and Incomplete Observability,” IEEE Transactions on Power Delivery, vol. 20, no. 4, pp. 2381–2388, Oct. 2005, doi: 10.1109/TPWRD.2005.855457. [5] A. G. Phadke, J. S. Thorp, and K. J. Karimi, “State Estimlatjon with Phasor Measurements,” IEEE Transactions on Power Systems, vol. 1, no. 1, pp. 233–238, 1986, doi: 10.1109/TPWRS.1986.4334878. [6] D. K. Mohanta, C. Murthy, and D. Sinha Roy, “A Brief Review of Phasor Measurement Units as Sensors for Smart Grid,” Electric Power Components and Systems, vol. 44, no. 4, pp. 411–425, Feb. 2016, doi: 10.1080/15325008.2015.1117538. [7] N. M. Manousakis, G. N. Korres, and P. S. Georgilakis, “Optimal placement of phasor measurement units: A literature review,” in 2011 16th International Conference on Intelligent System Applications to Power Systems, IEEE, Sep. 2011, pp. 1–6. doi: 10.1109/ISAP.2011.6082183. [8] J. Chen and A. Abur, “Placement of PMUs to Enable Bad Data Detection in State Estimation,” IEEE Transactions on Power Systems, vol. 21, no. 4, pp. 1608–1615, Nov. 2006, doi: 10.1109/TPWRS.2006.881149. [9] C. Rakpenthai, S. Premrudeepreechacharn, S. Uatrongjit, and N. R. Watson, “An Optimal PMU Placement Method Against Measurement Loss and Branch Outage,” IEEE Transactions on Power Delivery, vol. 22, no. 1, pp. 101–107, Jan. 2007, doi: 10.1109/TPWRD.2006.881425. [10] B. Gou, “Generalized Integer Linear Programming Formulation for Optimal PMU Placement,” IEEE Transactions on Power Systems, vol. 23, no. 3, pp. 1099–1104, Aug. 2008, doi: 10.1109/TPWRS.2008.926475. [11] B. Gou, “Optimal Placement of PMUs by Integer Linear Programming,” IEEE Transactions on Power Systems, vol. 23, no. 3, pp. 1525–1526, Aug. 2008, doi: 10.1109/TPWRS.2008.926723. [12] D. Dua, S. Dambhare, R. K. Gajbhiye, and S. A. Soman, “Optimal Multistage Scheduling of PMU Placement: An ILP Approach,” IEEE Transactions on Power Delivery, vol. 23, no. 4, pp. 1812–1820, Oct. 2008, doi: 10.1109/TPWRD.2008.919046. [13] N. H. Abbasy and H. M. Ismail, “A Unified Approach for the Optimal PMU Location for Power System State Estimation,” IEEE Transactions on Power Systems, vol. 24, no. 2, pp. 806–813, May 2009, doi: 10.1109/TPWRS.2009.2016596. [14] F. Aminifar, A. Khodaei, M. Fotuhi-Firuzabad, and M. Shahidehpour, “Contingency-Constrained PMU Placement in Power Networks,” IEEE Transactions on Power Systems, vol. 25, no. 1, pp. 516–523, Feb. 2010, doi: 10.1109/TPWRS.2009.2036470. [15] A. Enshaee, R. A. Hooshmand, and F. H. Fesharaki, “A new method for optimal placement of phasor measurement units to maintain full network observability under various contingencies,” Electric Power Systems Research, vol. 89, pp. 1–10, Aug. 2012, doi: 10.1016/j.epsr.2012.01.020. [16] S. Chakrabarti, E. Kyriakides, and D. G. Eliades, “Placement of Synchronized Measurements for Power System Observability,” IEEE Transactions on Power Delivery, vol. 24, no. 1, pp. 12–19, Jan. 2009, doi: 10.1109/TPWRD.2008.2008430. [17] E. K. Burke and G. Kendall, Eds., Search Methodologies. Boston, MA: Springer US, 2014. doi: 10.1007/978-1-4614-6940-7. [18] P. Gopakumar, M. J. B. Reddy, and D. K. Mohanta, “Novel multi-stage simulated annealing for optimal placement of PMUs in conjunction with conventional measurements,” in 2013 12th International Conference on Environment and Electrical Engineering, IEEE, May 2013, pp. 248–252. doi: 10.1109/EEEIC.2013.6549625. [19] B. Milosevic and M. Begovic, “Nondominated sorting genetic algorithm for optimal phasor measurement placement,” IEEE Transactions on Power Systems, vol. 18, no. 1, pp. 69–75, Feb. 2003, doi: 10.1109/TPWRS.2002.807064. [20] S. S. Geramian, H. A. Abyane, and K. Mazlumi, “Determination of optimal PMU placement for fault location using genetic algorithm,” in 2008 13th International Conference on Harmonics and Quality of Power, IEEE, Sep. 2008, pp. 1–5. doi: 10.1109/ICHQP.2008.4668810. [21] B. Allagui, H. Ben Aribia, and H. Hadj Abdallah, “Optimal placement of Phasor Measurement Units by genetic algorithm,” in 2012 First International Conference on Renewable Energies and Vehicular Technology, IEEE, Mar. 2012, pp. 434–439. doi: 10.1109/REVET.2012.6195309. [22] H. H. Müller and C. A. Castro, “Genetic algorithm?based phasor measurement unit placement method considering observability and security criteria,” IET Generation, Transmission & Distribution, vol. 10, no. 1, pp. 270–280, Jan. 2016, doi: 10.1049/iet-gtd.2015.1005. [23] S. Mandava, V. J, and R. V, “A Spanning Tree Approach in Placing Multi-channel and Minimum Channel PMU’s for Power System Observability,” International Journal of Electrical and Computer Engineering (IJECE), vol. 5, no. 3, p. 518, Jun. 2015, doi: 10.11591/ijece.v5i3.pp518-524. [24] K. M. Hassanin, A. A. Abdelsalam, and A. Y. Abdelaziz, “Optimal PMUs placement for full observability of electrical power systems using flower pollination algorithm,” in 2017 IEEE International Conference on Smart Energy Grid Engineering (SEGE), IEEE, Aug. 2017, pp. 20–25. doi: 10.1109/SEGE.2017.8052770. [25] J. Peng, Y. Sun, and H. F. Wang, “Optimal PMU placement for full network observability using Tabu search algorithm,” International Journal of Electrical Power & Energy Systems, vol. 28, no. 4, pp. 223–231, May 2006, doi: 10.1016/j.ijepes.2005.05.005. [26] T. Venkatesh and T. Jain, “Optimal PMU placement using best first search algorithm with pruning,” in 2014 Eighteenth National Power Systems Conference (NPSC), IEEE, Dec. 2014, pp. 1–5. doi: 10.1109/NPSC.2014.7103799. [27] A. Raj and C. Venkaiah, “Optimal PMU placement by teaching-learning based optimization algorithm,” in 2015 39th National Systems Conference (NSC), IEEE, Dec. 2015, pp. 1–6. doi: 10.1109/NATSYS.2015.7489080. [28] S. Azizi, A. S. Dobakhshari, S. A. Nezam Sarmadi, and A. M. Ranjbar, “Optimal PMU Placement by an Equivalent Linear Formulation for Exhaustive Search,” IEEE Trans Smart Grid, vol. 3, no. 1, pp. 174–182, Mar. 2012, doi: 10.1109/TSG.2011.2167163. [29] Fei Zeng, Hao Xu, Daonong Zhang, Xiaoyi Zhang, and Yubo Yuan, “A new strategy for optimal PMU placement based on limited exhaustive approach,” in 2014 International Conference on Power System Technology, IEEE, Oct. 2014, pp. 67–74. doi: 10.1109/POWERCON.2014.6993520. [30] K. Kaushal, P. Syal, and S. K. Sinha, “A Brief Study on Optimal Placement of Phasor Measurement Unit,” in 2018 3rd International Innovative Applications of Computational Intelligence on Power, Energy and Controls with their Impact on Humanity (CIPECH), IEEE, Nov. 2018, pp. 215–220. doi: 10.1109/CIPECH.2018.8724316. [31] A. Aziz G. Mabaning and J. Rel C. Orillaza, “Complete solution of optimal PMU placement using reduced exhaustive search,” in 2016 IEEE Region 10 Conference (TENCON), IEEE, Nov. 2016, pp. 823–826. doi: 10.1109/TENCON.2016.7848119. [32] J. Peppanen, T. Alquthami, D. Molina, and R. Harley, “Optimal PMU placement with binary PSO,” in 2012 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Sep. 2012, pp. 1475–1482. doi: 10.1109/ECCE.2012.6342640. [33] A. A. Saleh, A. S. Adail, and A. A. Wadoud, “Optimal phasor measurement units placement for full observability of power system using improved particle swarm optimisation,” IET Generation, Transmission & Distribution, vol. 11, no. 7, pp. 1794–1800, May 2017, doi: 10.1049/iet-gtd.2016.1636. [34] T. K. Maji and P. Acharjee, “Multiple solutions of optimal PMU placement using exponential binary PSO algorithm,” in 2015 Annual IEEE India Conference (INDICON), IEEE, Dec. 2015, pp. 1–6. doi: 10.1109/INDICON.2015.7443403. [35] Bo Wang, Dichen Liu, and Li Xiong, “Advance ACO system in optimizing power system PMU placement problem,” in 2009 IEEE 6th International Power Electronics and Motion Control Conference, IEEE, May 2009, pp. 2451–2453. doi: 10.1109/IPEMC.2009.5157814. [36] P.-W. Tsai and V. Istanda, “Review on cat swarm optimization algorithms,” in 2013 3rd International Conference on Consumer Electronics, Communications and Networks, IEEE, Nov. 2013, pp. 564–567. doi: 10.1109/CECNet.2013.6703394. [37] A. Srivastava and S. Maheswarapu, “Optimal PMU placement for complete power system observability using Binary Cat Swarm Optimization,” in 2015 International Conference on Energy Economics and Environment (ICEEE), IEEE, Mar. 2015, pp. 1–6. doi: 10.1109/EnergyEconomics.2015.7235114. [38] Subhashree Priyadarshini and Chinmoy K. Panigrahi, “Binary Grey Wolf Technique for optimal placement of Phasor Measurement Unit with full network observability,” Journal of Engineering Science and Technology, vol. 15, no. 5, pp. 2924–2938, 2020.

Copyright

Copyright © 2023 Wilis Negi, Ritula Thakur. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.