Applications of Fourier series and Fourier Transform in Electrical and Electronics Devices

Abstract

Fourier series are of great importance in both theoretical and ap­ plied mathematics. For orthonormal families of complex­valued functions Fourier Series are sums of the ?n that can approximate periodic, complex­valued functions with arbitrary precision. This paper will focus on the Fourier Series of the complex exponentials. Of the many possi­ ble methods of estimating complex­valued functions, Fourier series are especially attractive because uniform convergence of the Fourier series (as more terms are added) is guaranteed for continuous, bounded functions. Furthermore, the Fourier coe?cients are designed to minimize the square of the error from the actual function. Finally, complex exponentials are relatively simple to deal with and ubiquitous in physical phenomena. This paper ?rst de?nes generalized Fourier series, with an emphasis on the se­ ries with complex exponentials. Then, important properties of Fourier series are described and proved, and their relevance is explained. A com­ plete example is then given, and the paper concludes by brie?y mentioning some of the applications of Fourier series and the generalization of Fourier series, Fourier transforms. In the mid­eighteenth century, physical problems such as the conduction pat­ terns of heat and the study of vibrations and oscillations led to the study of Fourier series. Of central interest was the problem of how arbitrary real­valued functions could be represented by sums of simpler functions. As we shall see later, a Fourier series is an in?nite sum of trigonometric functions that can be used to model real­valued, periodic functions. We shall begin by giving a brief description of the trigonometric polynomials, and especially of their relation to the complex exponentials. The Fourier series, the founding principle behind the field of Fourier analysis, is an infinite expansion of function in terms sine’s and cosines. Fourier transform provides a continuous complex frequency of a function. It is useful in the study of frequency response of a filter, solution PDE, Discrete Fourier transform and FFT in the signals analysis. The advent of Fourier transformation method has greatly extended our ability to implement Fourier methods on digital multimedia visualization system. It covers the mathematical foundations of Digital signal processing (DSP), classical sound, synthesis algorithms and multi-time frequency domain analysis associated musical sound. In this paper, we are analysis of square wave in terms of Fourier component, may occur in electric circuits designed to handle sharply rising pulses and how to convert analog to digital system by using Fourier transform and its applications in electronics and digital multimedia visualization signal process of communication system.

Introduction

I. INTRODUCTION

The Fourier transformation is standard system analysis tool for viewing the spectral content of signal or sequence. The Fourier transform of sequence, commonly referred to as the discrete time Fourier transform or DTFT is not suitable for real-time implementation. The DTFT takes a sequence as input, but produces a continuous function of frequency as output. A close relative to the DTFT is discrete Fourier transform or DFT [1]. The DFT takes a finite length sequence as input and produces a finite length sequence as output.

When the DFT is implemented as an efficient algorithm it is called the Fast Fourier transformation (FFT). J. W. Cooley and J. W. Tukey are given credit for bringing the FFT to the world in their paper “An algorithm for the machine calculation of complex Fourier Series”, Mathematics Computation, Vol. 19, 1965, pp. 297-301. In retrospect, others had discovered the technique many years before. For instance, the great German mathematician Karl Friedrich Gauss (1777-1855) had used the method more than a century earlier. This early work was largely forgotten because it lacked tool to make it practical: the digital computer [2-10]. Cooley and Tukey are honoured because they discovered the FFT at the right time. Mathematics is everywhere in every phenomena, technology, observation, experiment etc.

All we need to do is to understand the logic hidden behind. In this i????????e????????????????????e in(−∞, ∞), then the F.T of ?(????) is denoted by £(?) and is define by  article we are focusing on application of Fourier series in electric circuit and communication system [11-13]. FT is name in the ?o????o???????? of Joseph Fourier (1749-1829), one of the greatest name in the history of mathematics and physics.

Mathematically speaking, the Fourier transform is a linear operator that maps a functional space to another function space and decomposes a function into another function of its frequency components. In particular, the fields of electronics, quantum mechanics, and electrodynamics all mark heavy use to Fourier series. Additionally, other methods based on the Fourier series, such that as the FFT (Fast Fourier Transform ???? ƒ????o???? Discrete Fourier Transform [DFT]), are particularly useful for the fields of Digital signal Processing (DSP) and Multi-channel sound analysis [14-22]. In this Study, we sketch the entire figure by using ?????????????e????????????i???????? 9.0.

There are many different FFT algorithms; the one presented here is simply the most common time by 20 or 30 present (so-called base-4FFTs or base-8 FFTs). Most importantly, both classes of FFT algorithm are fast enough to embed into modern digital osciioscopes, multimedia visualization, and electronics equipment. Thus, FFTs have many modern applications, such as Spectrum analyzers, digital signal processors (DSPs), multimedia visualization, digital to analog signal process, and telecommunications systems.

IV. THE SPECTRUM ANALYZER

In modern technology, an important instrument to any experimentalist is the spectrum Analyzer. This instrument reads a digital signal (usually a voltage) and provides the operator with the Fourier coefficients which correspond to each of the sine and cosine terms of the Fourier series expansion of digital signal. Suppose an instrument takes a time-domain signal, such as the amplitude of output voltage of an instrument. Let us call this digital signal (????). Then the DFT of (????) is

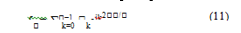
We see that this equation is of the same form of equation (7), which means that the previously described methods of the FFT apply to the function. Thus, any digital oscilloscope that is sufficiently fast and equipped with a FFT algorithm is capable of providing the user with the frequency components of the source signal. Oscilloscopes which are equipped with the ability to FFT their inputs are termed “Digital Spectral Analyzers”. Although they were once a separate piece of equipment for experimentalists, improvements in digital electronics has made it practical to merge the role of oscilloscopes. Spectrum Analyzer have many uses in the laboratory, but one of the most common uses in for signals gives the amplitudes of the various oscillatory components of the input. After normalization, this allows for the experimentalists to determine what frequencies dominate their signals. For example, if we have a DC signals, we would be expect the FFT to show only very low frequency oscillations (i.e., the largest amplitudes should correspond to ≈ 0 ). However, if we see a sharp peak of amplitudes around 60 HZ, we would know that something is feeding noise into our signal with a frequency of 60 HZ (for example, an AC leakage from our power source)

In other words, it can calculate the IFFT directly from the FFT; we are simply flipping the real and imaginary parts of the coefficients calculated by the original FFT. Thus, the IFFT algorithms are essentially the same as the FFT algorithm; all one must do is flip the numbers around at the beginning of the calculation. Since the IFFT inherits all of the speed benefits of the FFT, it is quite practical to use it in real time in the laboratory.

One of the most common applications of the IFFT in laboratory is to provide Digital signal processing (DSP). In general, the idea of DSP is to use configurable digital electronics to clean up, transform, or amplify a signal by FFT’ing the signal, removing, shifting or Damping the unwanted frequency components, and then transforming the signal back using the IFFT on the filtered signals.

There are many advantages to doing DSP as opposed to doing analog signal processing. To begin with, practically speaking, we can have a much more complicated filtering function (the function that transforms the coefficients of the DFT) with DSP than analog signal processing.

While it is fairly easy to make a single band pass, low pass, or high pass filter with capacitors, resistors, and inductors, it is relatively difficult and time consuming to implement anything more complicated than these three simple filters. Furthermore, even if a more complicated filter was implemented with analog electronics, it is difficult to make even small modification to the filter (there are exceptions to this, such as FPGA’s, but those are also more difficult to implement than sample software solution). DSP is not limited by either of those effects since the processing is (usually) done in software, which can be programmed to do whatever the user desires.

Probably the most important advantage that DSP has over analog signal processing is the fact that the processing may be done after the signal has been taken.

In modern-day experiments, raw data is often recorded during the experiment and corrected for noise in software during the analysis step.

If one filters the signal beforehand (with analog signal processing), it is possible that the later in the experiment, the experimenter could find that they filtered out good signals. The only option in this case is for experiment to be return. On the other hand, if the signal processing was done digitally, all that the experimenter has to do is edit their analysis code and rerun the analysis; this could save both time and money.

VI. PRELIMINARY

1. Communication: Fourier transform is essential to understand how to signals behaves when it passes through filter, amplifiers and communication multi-channel.
2. Data Analysis: Fourier transform can be used as high-pass, low-pass, and band- pass filters and it can also be applied to signals and noise estimation by encoding the time series.
3. Cell Phone: Every mobile device net-book, notebook, tablet and phone have been built in high speed cellular data connection, just like Fourier transform because sound may be represented by a complex combination of their waves. Human very easily perform Fourier transform mechanically every day. For example when we are in room with great deal of noise and you selectively hear our name above a noise, we have just performed Fourier series.
4. Input Transducer: The device that converts a physical signal from source to an electrical, mechanical, electronic signal more suitable for communicating.
5. Transmitter: The device that sends the transducer signal
6. Transmission Channel: The physical medium on which the signals is carried.
7. Receiver: The device that recover the transmitted signal from the channel.
8. Output Transducer: The device that converts the received signal back into useful quantity.

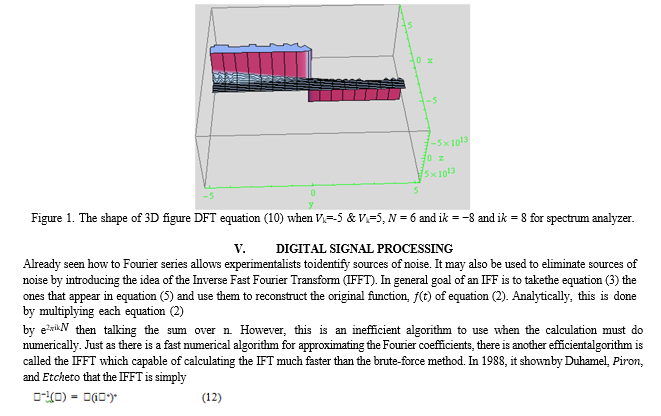
VII. PAIRS OF FREQUENCY USED IN DUAL-TONE MULTI-FREQUENCY DIGITAL SIGNAL

In above discussion, consider a list of set 12 channel frequency data is,

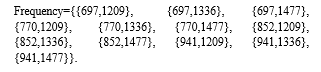
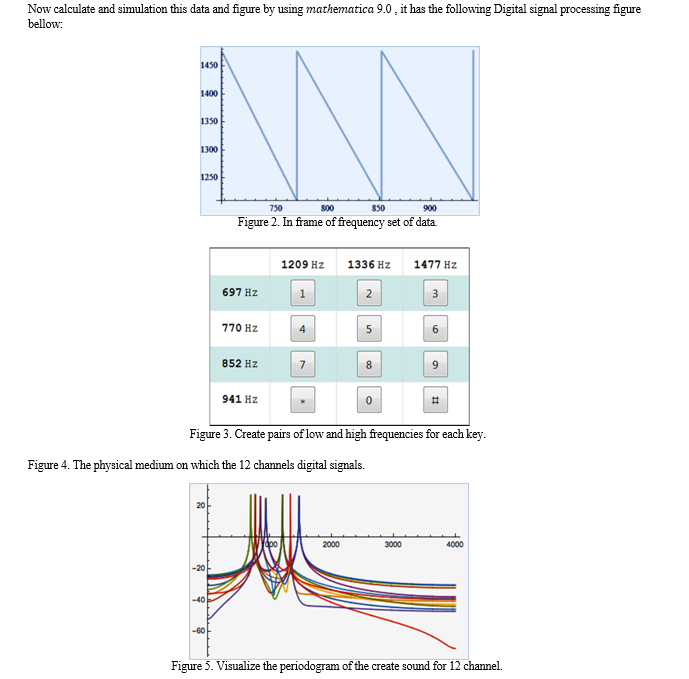
Now a days, in modern technology multimedia knowledge based over the internet in a user transparent way. The distributed knowledge based can be used to archive reasonable libraries of the multimedia objects. These multimedia objects can be retrieved in real time over the internet in user transparent manner, and applied for many task. The task could be display of animated cartoon, movies, simulation and visualization of complex objects transmission of complex VLSI design layouts, detail geographical maps.

Multimedia objects and their motion are displayed at client end a sequence of multimedia frames integrating synchronized digitalize video and sound at fast enough rate. Huge amount of data needs to be transmitted to display consecutive frames at such a rate, the size of the window, frame rate, the quality of the picture, the transmission bandwidth. Mathematical graph can be used the component level schematics of complex objects such as combustion device. The graph provided the ability to logically group the object and display the complex multiple digital visualization signals of 12-channel.

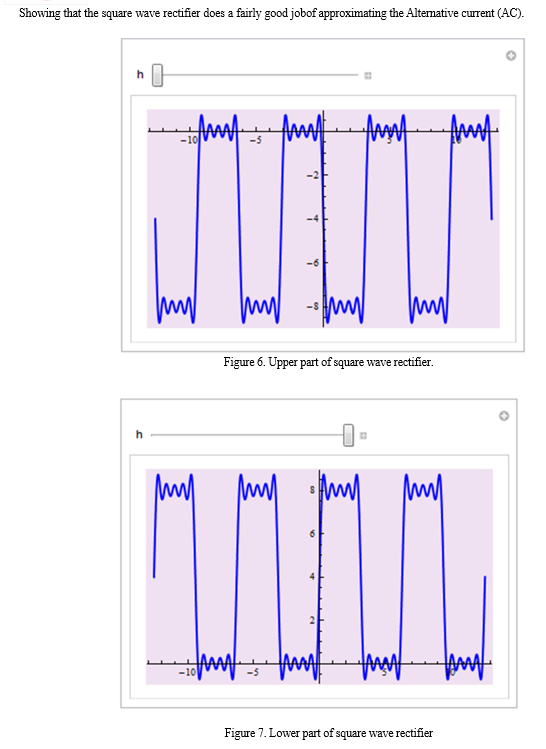
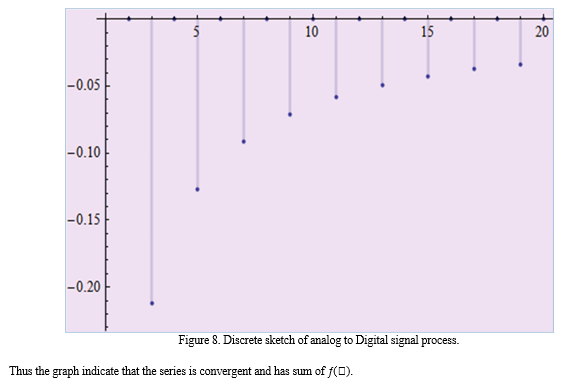
Conclusion

Fourier series is useful in many applications ranging from experimental instruments to rigorous mathematical analysis techniques. Thanks to modern developments in digital electronics and telecommunication. In this paper a brief overview Applications of Fourier transform. The primary use of Fourier transform of converting a time domain function into its frequency domain with digital communication signals. And we have seen Fourier converts signals from analog to digital signal, and how to square wave rectifier use in electricity. Fourier methods are commonly used for signal analysis and system design in modern electronics, The Spectrum Analyzer, information and communication technology. Like as cell phone, radio, television and vibration analysis. The Figure 1 represents the shape of 3D figure DFT equation (10) when ????k = ?5 & ????k = 5 & ???? = 6 and i???? = ?8 & i???? = 8 for spectrum analyzer it use in many laboratories. The Figure 2, Figure 3, Figure 4 represent pair wise frequency used in dual-tone multidimensional digital signal. The Figure 5 indicates the visualization periodogram creating the channel 12 frequency. The Figure 6, Figure 7 and Figure 9 and Figure 10 are square wave rectifier upper and lower part, the square wave rectifier does a fairly good job of approximating the Alternative current (AC). And Figure 8 discrete Fourier component analog to digital signal process. With these new techniques, Fourier series and Transforms have become an integral part of the toolboxes of mathematicians and scientists. Today, it is used for applications as diverse as ?le compression (such as the JPEG image format), signal processing in communications and astronomy, acoustics, optics, and cryptography.

References

Research in Science, Engineering and Technology, Vol. 6, Issue. 6, June 2017. [2] Hande, K. and FarhaVanu, “Application of Fourier series in communication system”, International Journal of Scientific and Engineering Research, Vol. 6, Issue 12, Dec- 2015, pp 24- 25. [3] Kaur, B., Sonia Sharma and Prince Verma, “Methodology of Multimedia and Visualization”, International Journal of Computer Application, Vol. 74, No. 16, July 2013, pp. 0975- 8887. [4] G. Jacobsen, Noise in digital optical transmission system, The Aetech House Library, London, 1994. [5] Y. F Wang application of diffusion processes in Robotics, optical communications and polymer science, Ph.D. Dissertation, Johns Hopkins University, 2001.G. W Mackey, Induced representation of groups and quantum mechanics, Benjamin, New York and Amsterdam, 1968. [6] G. J. Foschini, G. Vannucci and L. J Greenstein, “Envelope statistics for filtered optical signals corrupted by phase noise”, IEEE Trans. On communication 37: 12 (Dec 1989), 1293- 1302. [7] Duhamel, p., piron, B., Etcheto, J. M.,” On computing the inverse DFT,” Acoustics, Speech and Signal processing, Vol. 36, no. 2, pp. 285-286, Feb-1988. [8] Weisstein, Eric W. “Generalize Fourier series” From Math World-A wolfram Web Resource. http://mathworld.wolfram web Resource. [9] Numerical Methods in C: The art of scientific computing 2nd edition. W. H. Press, S. A. Teukolsky, W T. Vetterling, B. P. Flannery. Ch. 12. [10] Subrahmonia J, Nathan KS, Perrone MP, writer dependent recognition of on-line unconstrained handwriting. International conference on Acoustics, Speech and Signal Processing (ICASSP) Atlanta, 7-10 May, 1996. [11] Krishna S, Nathan KSM, Beigi J, Subrahamonia GJ, Clary H, Maruyama H. Real-time on-line unconstrained handwriting recognition using statistical method, International conference on Acoustics, Speech and Signal Processing (ICASSP 1995). [12] JW. Cooley and J. W. Tukey. An algorithm for the machine calculation of complex Fourier Series Mathematics of computation, 19: 297-301, 1965. [13] I. J Good. The interaction algorithm and practical Fourier analysis, Journal Roy. Stat. Soc, 20: 361-372, 1958. [14] IEEE. Special issue on fast Fourier transforms. IEEE trans. On Audio and electro acoustics, AU-17: 65-186, 1969. [15] Morgenstern. Note on Lower bound of the linear complexity of the fast Fourier transform. JACM: Journal of the ACM, 20, 1969. [16] C. E. Shanon. Communication in presence of noise, proceeding of the IRE, 37: 10-20, January 1949. [17] Review of Fourier series and its Application in Mechanical Engineering analysis by Tai-Ran Hsu. [18] Modern Digital and Analog communication system by B. P Lathi and Zhi Ding. [19] Communication System (analog to Digital) by Sanjay Sharma. [20] M. J. Roberts, Fundamentals of Signals and Systems (McGraw Hill, 2006) 2nded. [21] M. N. S Charles K. Alexander, Fundamentals of Electric Circuits (McGraw Hill, 2006) 2nded.

Copyright

Copyright © 2023 Prof. Jayprakash Matlam, Prof. Suniilkumar Shende, Dr. Dipak G. Lanjewar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.