An Approach to Colliding Plane Waves in General Relativity

Abstract

For many years after Einstein proposed his general theory of relativity, only a few exact solutions were known. Today the situation is completely different, and we now have a vast number of such solutions. However, very few are well understood in the sense that they can be clearly interpreted as the fields of real physical sources. The obvious exceptions are the Schwarzschild and Kerr solutions. These have been very thoroughly analysed, and clearly describe the gravitational fields surrounding static and rotating black holes respectively. In practice, one of the great difficulties of relating the particular features of general relativity to real physical problems, arises from the high degree of non-linearity of the field equations. Although the linearized theory has been used in some applications, its use is severely limited. Many of the most interesting properties of space-time, such as the occurrence of singularities, are consequences of the non-linearity of the equations.

Introduction

I. INTRODUCTION

The subject to be discussed in this paper is the collision and interaction of gravitational and electromagnetic waves. This is a particularly important topic in general relativity since the theory predicts that there will be a non-linear interaction between such waves. The effect of the non-linearity, however, is unclear. It is appropriate therefore to look in some detail at the simplest possible situation in which the effect of the non-linearity will be manifest: namely the interaction between colliding plane waves.  

 A. Why Consider Wave Interactions?

In classical theory, Maxwell’s equations are linear. An immediate consequence of this is that solutions can be simply superposed. This leads to the prediction that electromagnetic waves pass through each other without any interaction. This prediction is very thoroughly confirmed by observations. Radio waves are transmitted at many different frequencies, yet it is possible for a receiver to select any one particular station and to receive that signal almost exactly as it was transmitted. The only interference that is detected arises from other transmitters using the same frequency, and from the difficulty of isolating just one frequency within the receiver. After many years’ experience, no interaction has ever been detected between propagating electromagnetic waves. This applies not just to radio waves, but to all types of electromagnetic radiation, including light. That we can see clearly through a vacuum, even though light is also passing through it in other directions undetected, is one of the best established of scientific observations. More remarkably, this applies not just to local phenomena, but to the vast regions of space. The light that reaches us from distant galaxies arrives without any apparent interaction with the light that must have crossed its path during the millions of years that it takes to reach us. The apparent linearity of the field equations for electromagnetic waves is thus one of the best established scientific facts. However, this is not the entire story. Einstein’s equations which describe gravitational fields are highly non-linear. It follows that gravitational waves, if they exist, cannot pass through each other without a significant interaction. In this book we will be using the standard general theory of relativity.

In this theory gravitational waves are predicted, though their magnitudes are so small that the possibility of detecting them is only just coming within the scope of the most sophisticated modern apparatus. The purpose of this book is to contribute to an understanding of the character of the interaction that is theoretically predicted between gravitational waves. In Einstein’s theory, gravitational waves are considered as perturbations of space-time curvature that propagate with the speed of light. As these waves pass through each other, theoretically there will be a nonlinear interaction through the gravitational field equations. It will be necessary to consider the general character of these interactions, and how the propagating waves are modified by them  Consider again electromagnetic waves. According to Einstein’s theory, all forms of energy have an associated gravitational field. Electromagnetic waves must therefore be coupled to an associated perturbation in the space-time curvature. In the full Einstein–Maxwell theory, Maxwell’s equations describing the electromagnetic field remain linear, indicating that there is no direct electromagnetic interaction between waves.

However, Einstein’s equations, which apply to the gravitational field, are highly non-linear. Thus, as two electromagnetic waves pass through each other, there will be a non-linear interaction between them due to their associated gravitational fields. This non-linear interaction between electromagnetic waves that is predicted by Einstein’s theory must necessarily be very small in order to be consistent with the fact that such interactions have not yet been detected. An interaction, however, is predicted, though its magnitude is likely to be similar to that between gravitational waves. Since the interactions we will be considering are so weak, it may be considered appropriate initially to use approximation techniques. A number of authors have considered this approach. The modern techniques of numerical relativity have also produced some interesting results. However, these approaches will not be used in this book. The method adopted here will be to concentrate on exact solutions of the Einstein–Maxwell field equations. This has the advantage of being able to clarify something of the global structure of wave interactions. This turns out to be one of their most remarkable features. It leaves us, however, with the problem of finding exact solutions, and these are only possible in a very limited number of situations.

B. Simplifying Assumptions

The problem that is to be considered in this book is the interaction between two waves. A simple case in which the waves propagate in the same direction has been analysed by Bonnor (1969) and Aichelburg (1971). They have found that, for the class of vacuum pp-waves that will be defined in Section 4.1, the waves can be simply superposed without interaction because of the linearity of the field equations when written in a certain privileged class of coordinate system. It is therefore appropriate to concentrate on the general case in which the waves propagate in arbitrary different directions. In this case it is always possible to make a Lorentz transformation to a frame of reference in which the waves approach each other from exactly opposite spatial directions. It is therefore only necessary to consider the ‘head on’ collision between the two waves. However, even this situation is too difficult to analyse without some further simplifying assumptions. In order to obtain exact solutions, it is appropriate initially to make the additional assumption that the approaching waves have plane symmetry. This is a very severe restriction indeed, even though we intuitively think of plane fronted waves as approximations to spherical waves at large distances from their sources. However, the two cases must be distinguished as their global features are totally different. The waves we will be considering not only have a plane wave front, but also have infinite extent in all directions in the plane. In contrast, waves generated by finite sources must have curved wave fronts, but it is very difficult to set up boundary conditions and field equations for the interactions between such waves. The reason for concentrating on plane waves is that in this case it is possible to formulate the problem explicitly and to find exact solutions. In addition to the assumption that the wave front is plane, the imposition of plane symmetry also requires that the magnitude of the wave is constant over the entire plane. Further, it is appropriate to concentrate on ‘head on’ collisions and thus to impose the condition of global plane symmetry. It is always possible to make a Lorentz transformation to include oblique collisions but the physical interpretation of the solutions is now severely restricted by the above assumptions. The situation being considered in this book is thus the very restrictive one in which two waves, each with plane symmetry, approach each other from exactly opposite directions. A topic of further research will be to consider how to apply the qualitative results obtained here to more realistic situations, involving waves originating in physical sources. In the absence of more realistic exact solutions, however, the solutions described here form an important first step in an understanding of the non-linear interaction that occurs between waves in Einstein’s theory.

II. ELEMENTS OF GENERAL RELATIVITY

It is not the purpose of this chapter to introduce or explain Einstein’s general theory of relativity, since the reader who is not already familiar with it is unlikely to gain much from this book. The main purpose here is simply to clarify the notation that will be used. It is also appropriate in this chapter to briefly introduce the Newman–Penrose formalism which facilitates the geometrical analysis of the colliding plane wave problem and which will be used in Chapter 6 to derive the field equations.

A. Basic Notation

Basically, we will be following a very traditional approach, and the notation adopted will be that of the well known paper of Newman and Penrose (1962). Accordingly, a space-time will be represented by a connected C∞ Hausdorff manifold M together with a locally Lorentz metric gµν with signature (+, −, −, −) and a symmetric linear connection Γλ µν. Greek indices are used to indicate the values 0,1,2,3, and the covariant derivative of a vector is given by

These components can be considered to define the amount of curvature that is directly generated by the matter fields that are present at any location. For a vacuum field they will be zero, but they will be non-zero when electromagnetic waves or other fields are present. The components of the Weyl tensor, on the other hand, define the ‘free gravitational field’. They may be considered as describing the components of curvature that are not generated locally. In this sense they describe the pure gravitational field components. They may be interpreted as the components of gravitational waves, or of gravitational fields generated by non-local sources.

where R = Rαα is the curvature scalar. These two groups of components have different physical interpretations. The components of the Ricci tensor are related to the energymomentum tensor Tµν of the matter field present, through Einstein’s equation.

These components can be considered to define the amount of curvature that is directly generated by the matter fields that are present at any location. For a vacuum field they will be zero, but they will be non-zero when electromagnetic waves or other fields are present. The components of the Weyl tensor, on the other hand, define the ‘free gravitational field’. They may be considered as describing the components of curvature that are not generated locally. In this sense they describe the pure gravitational field components. They may be interpreted as the components of gravitational waves, or of gravitational fields generated by non-local sources.

B. Components of the Curvature Tensor

It is convenient to represent the curvature tensor in terms of distinct sets of components. Not only may it be divided into the Weyl and Ricci tensors, but each of these tensors may be described in terms of distinct components. The appropriate notation here is that of Newman and Penrose (1962). It is found to be convenient to introduce a tetrad system of null vectors. These include two real null vectors lµ and nµ, a complex null vector mµ, and its conjugate. They are defined such that their only nonzero inner products are

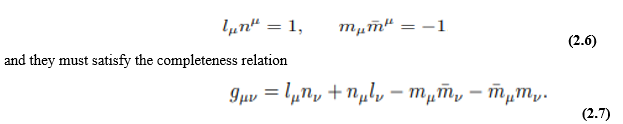
Having defined a tetrad basis, the Ricci and Weyl tensors may now be expressed in terms of their tetrad components. The ten independent components of the Ricci tensor can conveniently be divided into a component Λ representing the curvature scalar and the nine independent components of a Hermitian 3 × 3 matrix ΦAB which represents the trace free part of the Ricci tensor and satisfies

The ten independent components of the Weyl tensor, representing the free gravitational field, can more conveniently be expressed as the five complex scalars

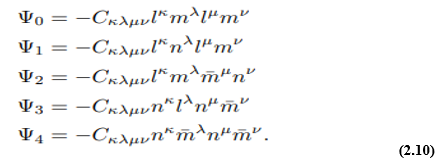
These components have distinct physical interpretations that will be mentioned below. They also have particular convenience when considering the algebraic classification of the space-time. Gravitational fields are usually classified according to the Petrov– Penrose classification of the Weyl tensor. This is based on the number of its distinct principal null directions and the number of times these are repeated. This classification is most conveniently described using a spinor approach. However, there is no need to introduce spinors here, as tetrads are sufficient. According to the tetrad approach, a null vector kµ is said to describe a principal null direction of the gravitational field with multiplicity 1, 2, 3 or4if it satisfies respectively

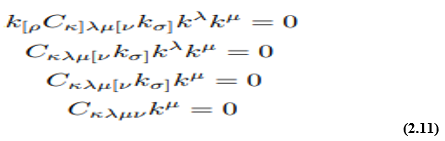
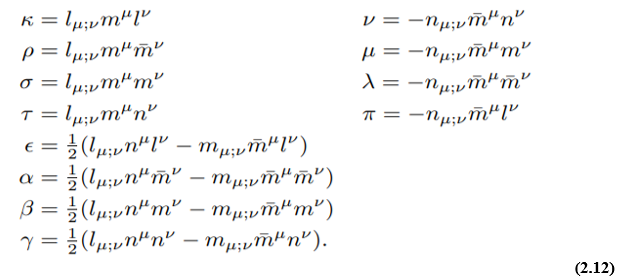
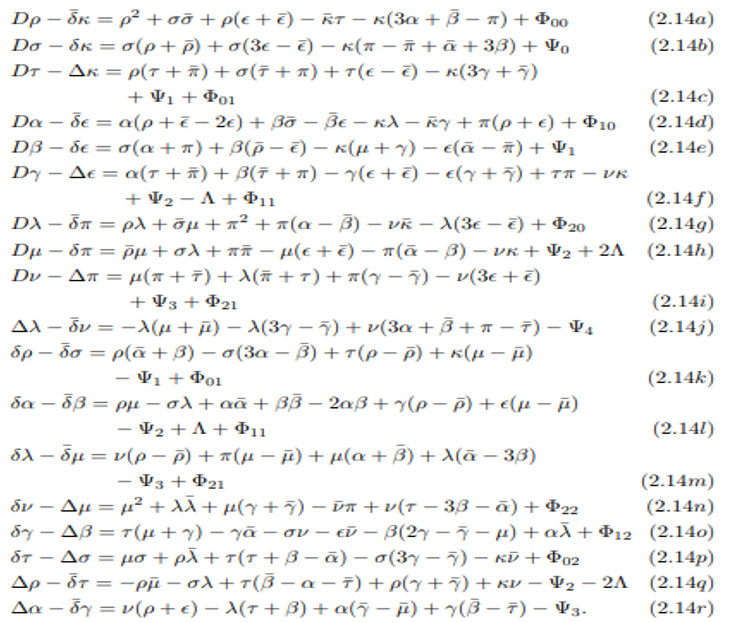
We will also require the commutation relations between the intrinsic derivatives. When applied to scalar functions, these are given by

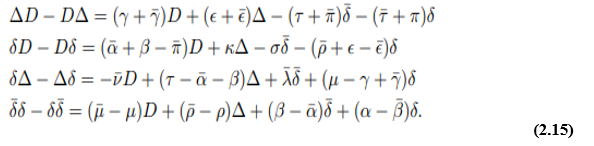
These can be applied to the coordinates to give the so-called metric equations, and also to the spin coefficients and the curvature tensor components.

An essential part of the general Newman–Penrose formalism is the set of Bianchi identies. These, however, will not be used explicitly in this text and therefore do not need to be repeated here.

Conclusion

Any interpretation of the above results concerning the collision of plane waves must bear in mind the fact that the situation is highly idealized. Nevertheless, some general features concerning the interaction of waves in general relativity may be indicated. A similar situation is well known in cosmology. Here the general expansion and, particularly, the initial singularity of the Friedmann universes turn out to be general features of relativistic cosmologies, rather than particular consequences of the high degree of symmetry that is assumed. In the case of colliding plane waves, the basic feature that has been substantially demonstrated above is the focusing effect of gravitational waves, and the slightly different focusing effects of waves of other types of matter. When two waves pass through each other, they will inevitably tend to focus each other. In the exact solutions that have been presented, the approaching waves are non-expanding. Thus, after the collision, the two waves will increasingly contract towards a focus. A wave crossing a gravitational wave will be focused astigmatically. Had the approaching waves been initially expanding, then it is reasonable to assume that, after the collision, their expansion would be slightly reduced.

References

[1] Adams, P. J., Hellings, R. W., Zimmerman, R. L., Farhoosh, H., Levine, D. I. and Zeldich, S. (1982). Inhomogeneous cosmology: gravitational radiation in Bianchi backgrounds. Astrophys. J., 253, 1–18. [2] Aichelburg, P. C. (1971). Remark on the superposition principle for gravitational waves. Acta Phys. Austriaca, 34, 279–84. [3] Aichelburg, P. C. and Sexl, R. U. (1971). On the gravitational field of a massless particle. Gen. Rel. Grav., 2,303–12. [4] Alekseev, G. A. and Khlebnikov, V. I. (1978). Newman-Penrose formalism and its applications in general relativity. Sov. J. Part. and Nucl., 9, 421–51. [5] Babala, D. (1987). Collision of a gravitational impulsive wave with a shell of null dust. Class. Quantum Grav., 4, L89–93. [6] Bade, W. L. and Jehle, H. (1953). An introduction to spinors. Rev. Mod. Phys., 25, 714–28. [7] Baldwin, O. R. and Jeffery, G. B. (1926). The relativity theory of plane waves. Proc. Roy. Soc. A, 111, 95. [8] Belinskii, V. A. and Zakharov, V. E. (1978). Integration of the Einstein equations by the inverse scattering method and calculation of exact soliton solutions. (Zh. Eksp. Teor. Fiz., 75, 1955–71) [9] Sov. Phys. JETP, 48, 985–94. Belinskii, V. A. and Zakharov, V. E. (1979). Stationary gravitational solutions with axial symmetry. (Zh. Eksp. Teor. Fiz., 77, 3-19) [10] Sov. Phys. JETP, 50, 1–9. Bell, P. and Szekeres, P. (1974). Interacting electromagnetic shock waves in general relativity. Gen. Rel. Grav., 5, 275–86. [11] Bertotti, B. (1959). Uniform electromagnetic field in general relativity. Phys. Rev., 116, 1331–3. [12] Blazhenova-Mikulich, L. Ju. and Sibgatullin, N. R. (1982). The automodel collision of plane neutrino waves in general relativity. Vestnik Moskovskii Universitet Seriia 1, 1982, 6, 83–90. [13] Bondi, H. and Pirani, F. A. E. (1989). Gravitational waves in general relativity. XIII. Caustic property of plane waves. Proc. Roy. Soc. A, 421, 395–410. [14] Bondi, H., Pirani, F. A. E. and Robinson, I. (1959). Gravitational waves in general relativity. III. Exact plane waves. Proc. Roy. Soc. A, 251, 519–33. [15] Bonnor, W. B. (1961). Exact solutions of the Einstein–Maxwell equations. Z. Phys., 161, 439–44. [16] Bonnor, W. B. (1969). The gravitational field of light. Comm. Math. Phys., 13, 163–74. [17] Bonnor, W. B. and Vickers, P. A. (1981). Junction conditions in general relativity. Gen. Rel. Grav., 13, 29–36. [18] Brinkmann, M. W. (1923). On Riemann spaces conformal to Euclidean space. Proc. Natl. Acad. Sci. U.S.A., 9, 1–3

Copyright

Copyright © 2022 Dr. Shailendra Kumar Srivastava. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.