Are Quantum Computers Threat to Privacy?

Abstract

Quantum computers work in a fundamentally different way from classical computers. Each qubit is in a superposition of 0 and 1 and can be used to store information. Quantum computers have the potential to revolutionize many industries. They can solve exponentially more difficult problems than conventional computers in seconds. Encryption is the process of turning plain text into ciphertext using a key. By measuring the quantum register we can find the marked number. Grover\'s algorithm can be used to solve a variety of problems related to finding an item in an unsorted database, such as cryptography, optimization, or machine learning. The main limitation of Grover\'s algorithm is that it is probabilistic. This means that there is a chance that the algorithm will not find the highlighted item after a certain number of iterations. However, the probability that the algorithm does not find the highlighted element decreases exponentially with the number of iterations. The Grover algorithm is a powerful quantum algorithm with many potential applications. However, it is still only a theoretical algorithm and has not been implemented on actual quantum computers. .. Many challenges must be overcome before the Grover algorithm can be used to solve real-world problems.

Introduction

I. INTRODUCTION

Quantum computers work in a fundamentally different way than classical computers. Classical computers use bits to store information, and each bit can only be in one of two states: 0 or 1. Quantum computers use qubits to store information, and each qubit can be in a superposition of both 0 and 1 at the same time. This is what gives quantum computers their incredible potential for speed and power.

Here is a simplified explanation of how a quantum computer works:

1. A quantum computer is initialized with a set of qubits, each of which is in a superposition of 0 and 1.
2. A quantum algorithm is applied to the qubits, which causes them to interact with each other in a way that depends on the problem that the computer is trying to solve.
3. The qubits are then measured, which collapses their superposition and produces a result.

The power of quantum computers comes from the fact that they can solve problems that are exponentially more difficult for classical computers. For example, a quantum computer could factor a 100-digit number in a matter of seconds, while a classical computer would take billions of years.

Quantum computers are still in their early stages of development, but they have the potential to revolutionize many industries, including cryptography, drug discovery, and artificial intelligence.

II. HOW ENCRYPTION WORKS [1]

Encryption is a way of scrambling data so that only authorized parties can understand the information. In technical terms, it is the process of converting human-readable plaintext to incomprehensible text, also known as ciphertext. In simpler terms, encryption takes readable data and alters it so that it appears random. Encryption requires the use of a cryptographic key: a set of mathematical values that both the sender and the recipient of an encrypted message agree on.

Encryption is the process of transforming information in such a way that it becomes unreadable to anyone who does not have the key to unlock it. This technique is used to keep sensitive information, such as personal data, financial information, and government secrets, secure.[1]

The encryption process begins with a message in its original form, called plaintext. The plaintext is then transformed using an algorithm, which is a set of rules for the encryption process. The output of this transformation is known as ciphertext, which cannot be understood by anyone without the decryption key. The key is typically a unique code or password that only the intended recipient has access to.

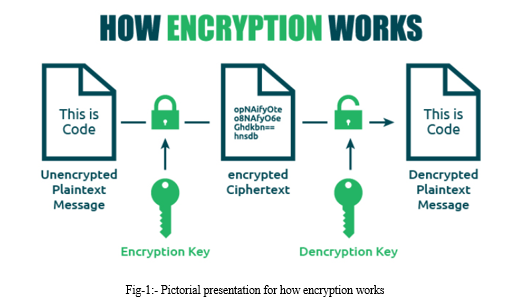
There are two main types of encryption: symmetric encryption and asymmetric encryption. Symmetric encryption involves using a single key for both encryption and decryption, while asymmetric encryption, also known as public-key encryption, uses two different keys - a public key for encryption and a private key for decryption.

In symmetric encryption, the plaintext is transformed into ciphertext using the same key that is used to decrypt the ciphertext back into plaintext. This key is shared between the sender and recipient of the message. Examples of commonly used symmetric encryption algorithms are Advanced Encryption Standard (AES), Triple DES, and Blowfish.

Asymmetric encryption, on the other hand, uses two different keys - a public key and a private key. The public key is used to encrypt the message, while the private key is used to decrypt it. The recipient of the message has a private key that allows them to decode the ciphertext. Examples of commonly used asymmetric encryption algorithms are RSA and Elliptic Curve Cryptography.

Encryption is applied to various types of data, including emails, files, and network connections. It is also used in many different areas beyond cybersecurity such as in banking, healthcare, communications, and online shopping. The encryption algorithm used will vary depending on the application and level of security required.

In conclusion, encryption works by transforming plaintext into an unreadable ciphertext. The encryption key is responsible for unlocking the encrypted message so that it can be read by the intended recipient. Encryption plays a crucial role in maintaining the confidentiality of sensitive information in today's digitally interconnected world.

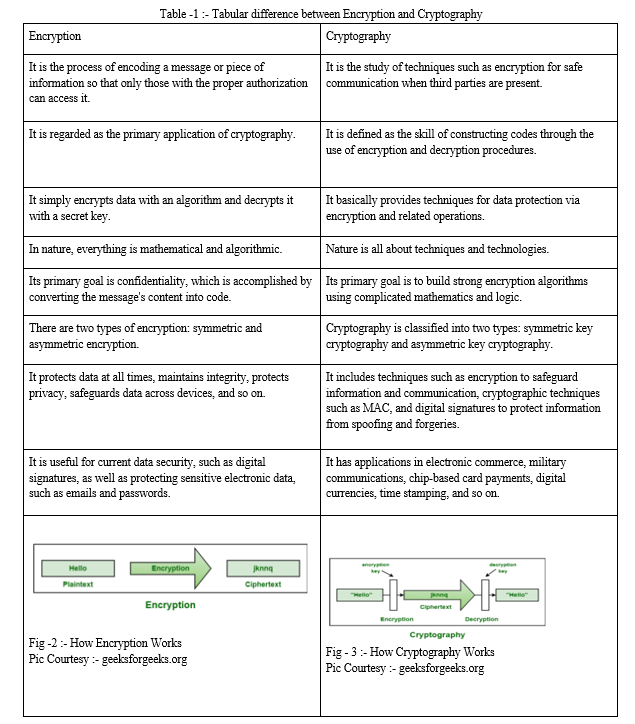
III. WHAT IS CRYPTOGRAPHY?

The practise of using codes to secure data and communications so that only the intended audience can read and process it is known as cryptography.

Symmetric key encryption and asymmetric key encryption are the two major types of encryption used in cryptography.

Data is encrypted and decrypted using the same key in symmetric key encryption. This kind of encryption is frequently employed for speed-sensitive applications like file encryption and secure communication.

Two keys are used in asymmetric key encryption: a public key and a private key. Data is encrypted using the public key, and decrypted using the private key. Applications like digital signatures, where security is crucial, frequently utilise this kind of encryption

IV. HOW CRYPTOGRAPHY WORKS?

A plaintext, often referred to as a cleartext, is transformed by cryptography into something that can only be understood by the intended recipients. This information shouldn't be accessible to anyone else, thus they shouldn't be able to comprehend it.

Encryption practises involve the conversion of plaintext into ciphertext. Decryption procedures are used to convert ciphertext into plaintext.

V. CAN ENCRYPTION BE BROKEN?

A. Brute Force Attacks

In a brute force attack, an attacker systematically tests every possible key until the correct one is discovered. This method can be highly effective against weak or short keys but becomes exponentially less feasible as the key length increases.

For instance, a key with a length of 128 bits has 2^128 possible combinations, making a brute force attack computationally infeasible even for the most powerful supercomputers.

Brute force attacks can be mitigated by using longer keys and strong encryption algorithms. Modern encryption standards like AES (Advanced Encryption Standard) employ keys that are sufficiently long to resist brute force attacks, given the current state of computational technology.

B. Cryptanalysis

Cryptanalysis is the art and science of deciphering encrypted messages and breaking cryptographic systems, often with the goal of uncovering the underlying plaintext or the secret encryption key. It involves a careful analysis of the encryption algorithms' vulnerabilities, weaknesses, and patterns. Cryptanalysts employ a variety of sophisticated techniques to exploit flaws in cryptographic systems and recover sensitive information. These techniques range from mathematical analyses that exploit structural weaknesses in algorithms to statistical methods that exploit patterns in ciphertext and plaintext relationships. Cryptanalysis can be broadly categorized into two main types: brute force attacks, which involve trying all possible keys, and more advanced methods that take advantage of the algorithms' intrinsic properties. The field of cryptanalysis has a rich history, with classic examples including the breaking of the Enigma machine during World War II and the more recent discovery of vulnerabilities in widely used encryption protocols. Cryptanalysts play a critical role in assessing the security of encryption systems and driving the development of stronger cryptographic techniques. In the digital age, where secure communication and data protection are paramount, cryptanalysis remains an indispensable component of the larger field of cryptography. [2]

C. Side-Channel Attacks

Side-channel attacks are a class of cryptographic attacks that exploit information leaked during the execution of an encryption algorithm, rather than attempting to directly break the algorithm's mathematical properties. These attacks target unintended information channels, such as power consumption, timing, electromagnetic radiation, or even sound, which can reveal information about the internal operations of a cryptographic device. By analyzing these side-channel signals, attackers can deduce sensitive information such as encryption keys. Side-channel attacks are particularly concerning because they often bypass the mathematical strength of the encryption algorithm itself and exploit the physical implementation or environment in which the algorithm runs. Examples of side-channel attacks include Differential Power Analysis (DPA), Timing Attacks, and Electromagnetic Analysis (EMA). [3]

VI. IS IT DIFFICULT TO BREAK ENCRYPTION WITHOUT QUANTUM COMPUTING?

Yes, it is very difficult to break encryption without quantum computing. The current encryption methods used to protect data are based on mathematical problems that are very difficult to solve for classical computers. For example, the RSA encryption algorithm uses the difficulty of factoring large numbers to protect data. A classical computer would take billions of years to factor a large number, such as the 2048-bit RSA key used to protect most online banking transactions.

However, quantum computers could potentially break these encryption methods much faster. Quantum computers use a different computing architecture that can solve certain types of problems, such as factoring large numbers, much faster than classical computers. For example, Shor's algorithm is a quantum algorithm that can factor large numbers in polynomial time, which is much faster than the exponential time required by classical computers.

The development of quantum computers is still in its early stages, but it is likely that they will eventually be able to break current encryption methods. This is why it is important to start developing quantum-resistant encryption methods now.

There are a number of post-quantum encryption schemes being developed that are designed to be secure against quantum computers. These schemes use different mathematical problems that are more difficult for quantum computers to solve. However, it is important to note that no post-quantum encryption scheme is completely secure. It is possible that new quantum algorithms will be developed that can break these schemes.

The best way to protect data against quantum computers is to use a combination of encryption methods. This could include using a current encryption method for short-term protection and a post-quantum encryption method for long-term protection. It is also important to keep your software up to date, as new security updates may be released that protect against quantum attacks.

VII. QUANTUM FOURIER TRANSFORM

The Quantum Fourier Transform (QFT) is a fundamental quantum algorithmic technique that plays a pivotal role in many quantum algorithms, including Shor's algorithm for factoring large numbers and quantum phase estimation. It is the quantum analog of the classical Discrete Fourier Transform (DFT), but it harnesses the power of quantum superposition and entanglement to perform certain computations exponentially faster than their classical counterparts.

Quantum Fourier Transform:

The Quantum Fourier Transform transforms a quantum state representing amplitudes of different states into a state that encodes the frequency components of those amplitudes. In other words, it takes a quantum superposition of states and "reads" the underlying frequencies of that superposition.

For simplicity we are not diving into mathematics of QFT*

VIII. SHOR’S ALGORITHM

A. Bell’s Theorem [4]

“There is no physical theory for local hidden variables which can reproduce the quantum mechanics predictions.”

Explanation:-

A local hidden variable theory (LHV) is a theory that assumes that all physical processes are local, meaning that information and correlations cannot be propagated faster than the speed of light. It also assumes that there are hidden variables that determine the outcome of all measurements, even if we cannot directly observe them.

Bell's theorem states that no LHV theory can reproduce the predictions of quantum mechanics for certain experiments involving entangled particles. Entanglement is a phenomenon in which the quantum states of two or more particles are linked together, even when they are separated by a large distance.

The most famous example of an experiment that violates Bell's inequality is the Einstein-Podolsky-Rosen (EPR) experiment. In this experiment, two entangled photons are emitted from a source. The photons are then sent in opposite directions to two detectors. The detectors can be set to measure either the polarization of the photons (whether they are polarized vertically or horizontally) or the momentum of the photons (whether they have momentum in the leftward or rightward direction).

According to quantum mechanics, the polarization and momentum of the photons are entangled. This means that if we measure the polarization of one photon, we will instantly know the polarization of the other photon, no matter how far apart they are.

However, if there were LHVs, then the polarization of each photon would be determined by its hidden variables, and these hidden variables would not be affected by the measurement of the other photon. This means that the polarization of the two photons would not be entangled, and we would not be able to instantly know the polarization of one photon by measuring the other photon.

Bell's theorem shows that this is not possible. It proves that if LHVs exist, then the predictions of quantum mechanics for the EPR experiment would be different from what we actually observe. [5] [6]

The EPR experiment has been performed many times, and the results have always been consistent with the predictions of quantum mechanics. This means that either LHVs do not exist, or that quantum mechanics is incomplete and does not tell the whole story about reality.

The implications of Bell's theorem are still being debated by physicists. Some believe that it proves that quantum mechanics is fundamentally non-local, meaning that information can be propagated faster than the speed of light. Others believe that it is possible to reconcile quantum mechanics with local hidden variables, but that this would require a radical revision of our understanding of physics. The debate over Bell's theorem is likely to continue for many years to come. It is one of the most important and challenging problems in physics today.

B. Why Shor’s algorithm?

Shor's algorithm is used to decode encryption because it can factor large numbers exponentially faster than any known classical algorithm. This means that it could be used to break many of the most popular encryption schemes, such as RSA and Diffie-Hellman, which are based on the difficulty of factoring large numbers.

The security of these encryption schemes relies on the fact that it is computationally infeasible to factor large numbers. However, Shor's algorithm can factor numbers in polynomial time, which means that it could break these encryption schemes in a reasonable amount of time, given a sufficiently large quantum computer.

Shor's algorithm is more beneficial than other algorithms for decoding encryption because it is much faster. For example, a classical computer would need to try all possible combinations of factors to factor a large number, which could take billions of years. However, Shor's algorithm can factor a number in a matter of seconds or minutes.

The feasibility of Shor's algorithm depends on the development of practical quantum computers. Current quantum computers are still in their early stages of development, but they are getting more powerful every year. It is estimated that a quantum computer capable of breaking RSA encryption could be built within the next 10 to 20 years.

The development of Shor's algorithm has led to a lot of research into post-quantum cryptography, which is a field of cryptography that is designed to be secure against quantum computers. Post-quantum cryptography is still in its early stages of development, but it is a promising area of research that could help to protect our data from future quantum attacks.

Here are some of the benefits of Shor's algorithm over other algorithms for decoding encryption:

It is much faster.

It is more scalable.

It is more secure.

Shor's algorithm is a powerful tool that could have a major impact on the security of our data. However, it is important to note that Shor's algorithm is not a silver bullet. There are still other ways to protect our data from quantum attacks, such as post-quantum cryptography.

IX. HOW SHOR’S ALGORITHM WORKS

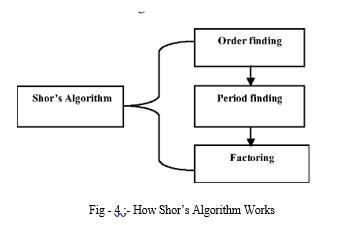
Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor. It is one of the few known quantum algorithms with compelling potential applications and strong evidence of superpolynomial speedup compared to best known classical (that is, non-quantum) algorithms.

The basic idea of Shor's algorithm is to convert the factoring problem into the problem of finding the period of a function. This can be done using a classical computer. The quantum part of the algorithm comes in when finding the period using the quantum Fourier transform.

Here is an example of how Shor's algorithm works. Let's say we want to factor the number 15. We first convert this into the problem of finding the period of the function f(x) = x^2 mod 15. This function takes an integer as input and returns the remainder when that integer is squared and divided by 15.

We can find the period of f(x) using the quantum Fourier transform. This is a quantum algorithm that can efficiently compute the Fourier transform of a function. The Fourier transform of a function is a way of representing the function as a sum of sine and cosine waves.

The quantum Fourier transform of f(x) will have a peak at the period of the function. So, by measuring the quantum Fourier transform of f(x), we can find the period of the function.

Once we know the period of f(x), we can factor 15 by finding the two numbers that divide 15 and have a product of the period. In this case, the period of f(x) is 4, so the two numbers that divide 15 and have a product of 4 are 3 and 5.

Shor's algorithm can be used to factor any integer that is the product of two primes. The time complexity of Shor's algorithm is exponential in the number of bits of the integer to be factored. This means that Shor's algorithm can factor much larger integers than any classical algorithm.

The development of Shor's algorithm has led to concerns about the security of certain cryptographic systems. For example, the RSA cryptosystem is based on the difficulty of factoring large numbers. If Shor's algorithm can be implemented on a practical quantum computer, then it could be used to break RSA and other cryptographic systems.

However, it is important to note that Shor's algorithm is still a theoretical algorithm. It has not yet been implemented on a practical quantum computer. There are many challenges that need to be overcome before Shor's algorithm can be used to factor large numbers in a practical way.

In Shor’s Algorithm, the Input is Non-prime number N and the Output is Non-trivial factor of N:-

NPUT (N) —> SHOR’S ALGORITHM —> OUTPUT (Non-trivial factor of N)

X. GROVER’S ALGORITHM

Grover's algorithm is a quantum algorithm that can find a marked item in an unsorted database with high probability, using only O(√N) queries, where N is the size of the database. This is much faster than the O(N) queries required by a classical algorithm, which gives Grover's algorithm a quadratic speedup.

The basic idea of Grover's algorithm is to use quantum superposition to create a state where all the items in the database are equally likely to be the marked item. The algorithm then applies a quantum operation called the Grover diffusion operator, which amplifies the probability of the marked item being in the superposition. This process is repeated until the probability of the marked item being in the superposition is high enough to be measured with high confidence.

Here is an example of how Grover's algorithm works. Let's say we have a database of 16 numbers, and one of the numbers is marked. We want to find the marked number using Grover's algorithm.

The first step is to initialize the quantum register to a uniform superposition over all the numbers in the database. This means that each number in the database has an equal probability of being the marked number.

The next step is to apply the Grover diffusion operator repeatedly. The Grover diffusion operator takes a quantum state and amplifies the probability of the marked item being in the state.

The number of times the Grover diffusion operator is applied depends on the size of the database. For a database of 16 numbers, the Grover diffusion operator must be applied 4 times.

After the Grover diffusion operator has been applied 4 times, the probability of the marked item being in the superposition is high enough to be measured with high confidence. By measuring the quantum register, we can find the marked number.

Grover's algorithm can be used to solve a variety of problems that involve searching for an item in an unsorted database, such as cryptography, optimization, or machine learning.

The main limitation of Grover's algorithm is that it is probabilistic. This means that there is a chance that the algorithm will not find the marked item after a certain number of iterations. However, the probability of the algorithm not finding the marked item decreases exponentially with the number of iterations.

Grover's algorithm is a powerful quantum algorithm with a wide range of potential applications. However, it is still a theoretical algorithm and has not yet been implemented on a practical quantum computer. There are many challenges that need to be overcome before Grover's algorithm can be used to solve real-world problems.

Conclusion

Quantum computers are a potential threat to privacy because they could be used to break current encryption methods. This could allow attackers to access sensitive data, such as financial information, medical records, and government secrets. However, it is important to note that quantum computers are still in their early stages of development. It is not clear when they will be powerful enough to break current encryption methods. In the meantime, there are a number of things that can be done to protect data privacy, such as using post-quantum cryptography and implementing strong security practices. Here are some of the ways quantum computers could impact data privacy: 1) They could be used to break current encryption methods, making it possible for attackers to access sensitive data. 2) They could be used to create new types of cyberattacks, such as those that target quantum-enabled devices. 3) They could be used to develop new ways to track and monitor people, such as by collecting and analyzing their personal data. The potential impact of quantum computers on data privacy is a serious concern. However, there are a number of things that can be done to mitigate this risk, such as developing new encryption methods and security practices that are resistant to quantum attacks. Here are some of the things that are being done to address the quantum computing threat to privacy: a) Researchers are developing new encryption methods that are resistant to quantum attacks. b) Governments are investing in research and development of quantum computing technologies. c) Companies are starting to adopt post-quantum cryptography. Security professionals are developing new security practices that are resistant to quantum attacks. The quantum computing threat to privacy is a complex issue. There is no easy solution, but by taking steps to mitigate the risk, we can help to protect our data and privacy in the future.

References

[1] https://www.cloudflare.com/learning/ssl/what-is-encryption/ [2] https://cloud.google.com/learn/what-is-encryption#:~:text=on%20every%20day.,How%20encryption%20works,also%20created =%20 by%20an%20algorithm. [3] https://www.comparitech.com/blog/information-security/cryptanalysis/ [4] https://eprint.iacr.org/2005/388.pdf [5] https://byjus.com/physics/bells-theorem/ [6] Stanford Encyclopedia of Philosophy article on \"Bell\'s theorem

Copyright

Copyright © 2023 Ishan Rahul Surdi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.