Background Noise Suppression in Audio File using LSTM Network

Abstract

In the realm of speech enhancement, noise suppression is a crucial problem. It is especially important in work-from-home situations where noise reduction may improve communication quality and reduce the cognitive effort of video conferencing. As a result of the advent of deep neural networks, several novel ways for audio processing methods based on deep models have been presented. The goal of the project is to use a stacked Dual signal Transformation LSTM Network (DTLN) to combine both analysis and synthesis into one model. The proposed model consists of two separation cores, the first of which employs an Short Term Fourier Transformation (STFT) signal transformation and the second of which employs a learnt signal representation, This arrangement was designed to enable the second core to further improve the signal with phase information while the first core creates a strong magnitude estimation. Due to the complementarity of traditional and learnt features modifications, this combination might give good impacts while preserving a minimal computing footprint, in terms of computational complexity, the stacked network is far less than most previously suggested LSTM networks and assures real-time capabilities.

Introduction

I. INTRODUCTION

Noise Suppression is the task of removing interferences from a degraded speech signal and thereby improving the perceived quality and intelligibility of the signal. The research interest in Noise suppression has been consistently high, due to challenges arising with applications such as mobile speech communication systems, hearing aids, and robust speech recognition. Single-channel speech enhancement in highly non-stationary noise conditions is a very challenging task, especially when interfering speech is included in the noise. Deep learning-based approaches have notably improved the performance of speech enhancement algorithms under such conditions the problem is solved using a two-stage approach. Long Short-Term Memory (LSTM), a special kind of Recurrent Neural Network (RNN), is capable of learning long-term dependencies. A mask-based long short-term memory (LSTM) network is employed for noise suppression. It is also able to increase intelligibility in low-SNR conditions and consistently outperforms all reference methods.

II. LITERATURE SURVEY

Davit Baghdasaryan [1] The majority of noise-reduction algorithms are subtractive, which means they look for frequencies with more background noise and subtract those bands from the original signal. Static filters, such as lowpass [2], highpass, and bandpass filters, are used in many of these systems. The sort of noise that is filtered and isolated is also clear. On the edge device – phones, laptops, conferencing systems, and so on — traditional noise reduction has shown to be successful. Since it's the edge device that collects the user's voice in the first place, this seems like a natural method. The gadget then filters out the noise and delivers the result to the opposite end of the line. Ten years ago, cell phone calling was a bad experience. Some mobile phones still have this feature; however, most recent phones include several microphones (mic) that help to reduce background noise when talking. Existing noise reduction technologies aren't perfect, but they do enhance the user experience. When employing separate microphones, the form factor comes into play. A minimum distance between the first and second microphones is required. It works great when the user places the phone on their ear and lips to speak. By analysing audio frame by frame, classic Digital Signal Processing (DSP) algorithms attempt to continually discover and adapt to the noise pattern. In some situations, these algorithms are effective. They do not, however, scale to the diversity and complexity of sounds encountered in our daily lives.

Fingscheidt T, et. al [3] Regression based on Neural Networks has led to considerable advances in speech enhancement under non-stationary noise conditions. Nonetheless, speech distortions can be introduced when employing Neural Networks trained to provide strong noise suppression. It addresses this problem by first suppressing noise and subsequently restoring speech with specifically chosen Neural Network topologies for each of these distinct tasks.

Maximilian Strake et. al [4] Classical speech enhancement algorithms typically operate in the short-time Fourier transform (STFT) domain and use a frequency bin-wise gain function, also called weighting rule, which is derived using an optimality criterion under specific model assumptions for the distributions of speech and/or noise. Commonly, estimates of the prior signal-to-noise ratio (SNR) and in turn the noise power are needed for the weighting rule computation. Numerous algorithms exist for the estimation of a priori SNR  and noise power.

Speech enhancement framework, classical and deep learning-based approaches

For the task of estimating the clean speech signal s(n) from a noisy microphone signal y(n), we employ a signal model of the form

y(n)=s(n)+d(n).............(1)

where the noise signal d(n) with the discrete-time sample index n is assumed to additively mix with s(n). The corresponding STFT domain representation, computed by applying a frame-wise window function with a frame length of L and a frame shift of R, followed by a K-point discrete Fourier transform (DFT), is given by

Y?(k)=S?(k)+D?(k) ..................(2)

with frame index ? and frequency bin index k∈K={0,1,…,K−1}k∈K={0,1,…,K−1}. Most of the classical speech enhancement approaches and also many deep learning-based approaches rely on estimating a frame- and frequency bin-wise gain function G?(k) to subsequently compute the estimated clean speech following

S^?(k)=G?(k)⋅Y?(k).........(3)

III. PROPOSED SYSTEM

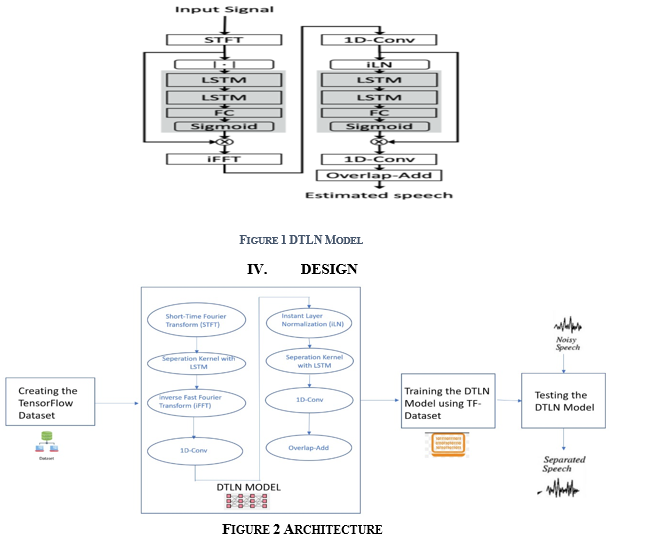
As a result, researchers created RNN variations that use gates to tackle this problem. Gates are operations that can learn how to add or delete information from a concealed state. Long Short-Term Memory is the neural network that employs these gates (LSTM). Two separation cores with two LSTM layers are followed by a fully-connected (FC) layer and sigmoid activation to provide a mask output in the stacked dual-signal transformation LSTM network design. The mask predicted by the FC layer and the sigmoid activation is multiplied by the magnitude of the mixture and translated back to the time domain using the phase of the input mixture without recreating the waveform in the first separation core. To produce the feature representation, a 1D-Conv layer processes the frames from the first network. The feature representation is processed by a normalization layer before it is fed to the second separation core. The unnormalized version of the feature representation is multiplied by the expected mask of the second core. The result is sent into a 1D-Conv layer, which converts the estimated representation back to the time domain. Finally, the signal is rebuilt using an overlap and addition process.

A. Create a Tensorflow Dataset

Class to create a Tensorflow dataset based on an iterator from a large scale audio dataset. This audio generator only supports single channel audio files.

i. It lists the data of the dataset and count the number of samples.

ii. Process the audio files

iii. create the dataset

B. DTLN Model

To create a mask output in the LSTM stacked double signal transform network architecture, two isolation cores with two LSTM layers are followed by a fully connected layer (FC) and sigmoid activation. The mix size is multiplied by the mask predicted by the FC layer and sigmoid activation, and the phase of the input mix is used to translate back to the time domain without recreating the waveform in the first separation kernel. A 1D-Conv layer processes frames from the first network to construct the feature representation. Before going to the second separation core, the feature representation is treated by a normalisation layer.The predicted mask of the second kernel is multiplied by the unnormalized version of the feature representation. The estimated representation is then transmitted to a 1DConv layer, which transforms it back to the time domain. Finally, superimposition and addition are used to recreate the signal.

Helper layers are defined

1. STFT Layer: STFT (Short-time Fast Fourier Transform) is a method for determining the sinusoidal frequency and phase content of tiny sections of a signal as they change over time. STFTs are calculated by splitting a larger temporal signal into equal-length segments and executing the Fourier transform on each segment separately. The layer calculates the STFT in the last dimension and returns its magnitude and phase.

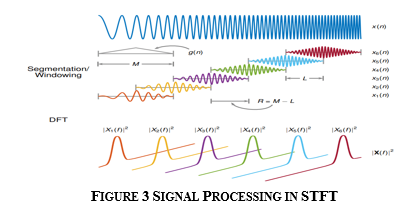
Discrete-time The data to be changed is transformed using STFT, which can be divided up into chunks or frames (which usually overlap each other, to reduce artefacts at the boundary). Each chunk is Fourier converted, and the resulting complex result is added to a matrix that stores magnitude and phase for each time and frequency point. This may be written as follows:

likewise, with signal x[n] and window w[n]. In this case, m is discrete and ω is continuous, but in most typical applications the STFT is performed on a computer using the fast Fourier transform, so both variables are discrete and quantized.

2. FFT Layer: The FFT (fast Fourier transform) decomposes a signal into its spectral components and so provides frequency information.

In the FFT formula, the DFT (discrete Fourier transform) equation, is decomposed into a number of short transforms and then recombined. 

On the last dimension, the layer executes a rFFT and returns the magnitude and phase of the STFT.

3. Seperation Kernel:

a. LSTM (Long Short-Term Memory) Layer: Long-term relationships between time steps in time series and sequence data are learned using an LSTM layer. The hidden state (also known as the output state) and the cell state are the two states of the layer. The output of the LSTM layer for time step t is stored in the hidden state at time step.

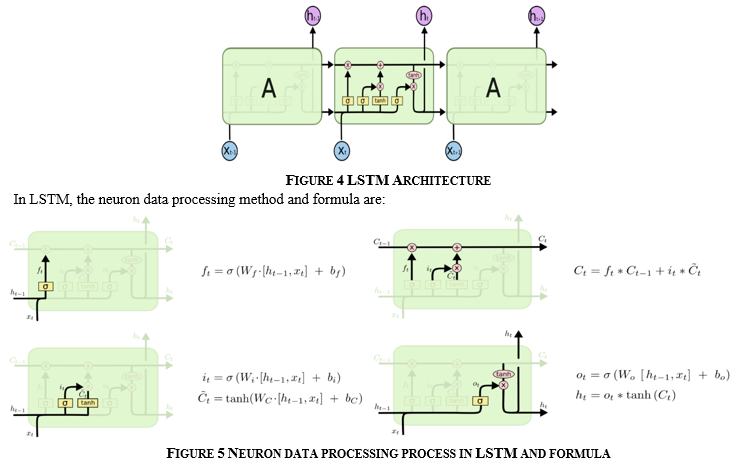
b. Fully Connected: The most general-purpose deep learning layer is the fully connected layer, also known as a dense or feed-forward layer. This layer has the least structure of all the ones we've created. It's utilised to change the size and shape of the output layer in almost all neural networks.

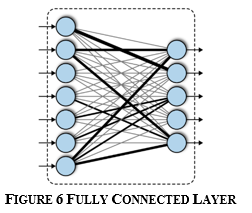
Mathematical form of a fully connected network is:

 Let x ∈ ? m represent the input to a fully connected layer. Let y i ∈ ? be the i -th output from the fully connected layer. Then y i ∈ ? is computed as follows:

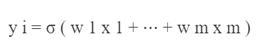
Here, σ is a nonlinear function (for now, think of σ as the sigmoid function introduced in the previous chapter), and the w i are learnable parameters in the network. The full output y is then:

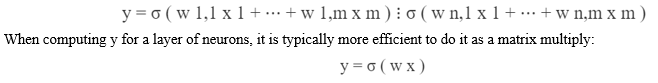
where sigma is a matrix in ? n×m and the nonlinearity σ is applied component wise.

c. Sigmoid: The sigmoid function is a type of logistic function that is commonly denoted as  σ(x) or sig(x).

σ(x) is given by:                 σ(x) = 1/(1+exp(-x))

The mixture's magnitude is multiplied by the mask predicted by the FC layer and sigmoid activation.

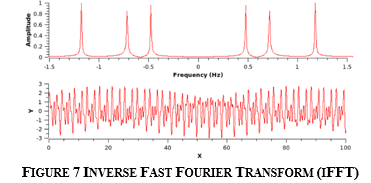
d. iFFT layer : IFFT is a DFT undoing algorithm. Backward Fourier Transform is another name for it. It transforms a frequency-domain signal from a space-domain signal. The distribution of value sequences to various frequency components produces the DFT signal. Using the Fourier transform to translate directly is computationally inefficient. As a result, the Fast Fourier transform is employed since it quickly computes the DFT matrix by factoring it as the product of sparse factors. This transformation is a translation from configuration space to frequency space, and it's critical for investigating both problem transformations for more efficient computing and signal power spectrum exploration. This is a translation from Xn to Xk. It involves the transformation of geographical or temporal data into frequency domain data.

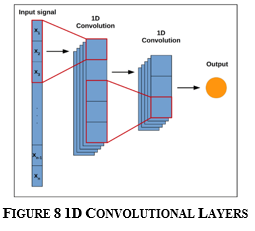
e. 1D- Conv: The 1D block consists of a configurable number of filters, each with a defined size; the vector and the filter are convolutioned, yielding a new vector with the same number of channels as the number of filters.

f. Instant Layer Normalization: Normalizing the distributions of intermediate layers is part of the layer normalisation process. Gradients that are smoother, training that is faster, and generalisation that is more accurate are all benefits.

A mini-batch of many instances with the same amount of characteristics is used to accomplish Instant Layer Normalization. Mini-batches are matrices (or tensors) in which one axis represents the batch and the other(or axes) represents the feature dimensions.

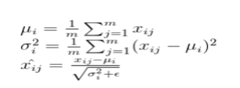
i represents batch and j represents features. x?,? is the i,j-th element of the input data.

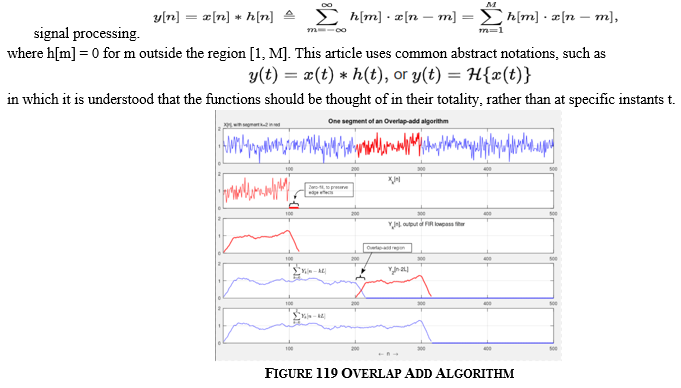
g. Overlap and Add Layer: From a framed signal, this layer reconstructs the waveform. The overlap–add technique is an effective way to assess the discrete convolution of a very lengthy signal x[n] with a finite impulse response (FIR)filter in

4. Build and Compile the DTLN Model: The model takes size (batchsize, len in samples) time domain batches and produces improved clips in the same dimensions. The Adam optimizer with a gradient norm clipping of 3 is utilised as the Training process optimizer. Two separation cores are included in the model. The first uses an STFT signal transformation, whereas the second uses a 1D-Conv layer to learn a transformation.

5.  Adam Optimizer: The optimizer rearranges assembler-language instructions, making it hard to link individual instructions to a line of source code. Adaptive Moment Estimation is a technique for optimising gradient descent algorithms. Adam combines the best characteristics of the AdaGrad and RMSProp techniques to provide a strategy for optimising noisy problems with sparse gradients. When working with huge problems with a lot of data or parameters, the approach is quite efficient. It is efficient and takes minimal memory. It's essentially a hybrid of the 'gradient descent with momentum' and the 'RMSP' algorithms.

6. Adam optimizer involves a combination of two gradient descent methodologies: 

a. Momentum:  By taking into account the 'exponentially weighted average' of the gradients, this approach is utilised to speed up the gradient descent algorithm. Using averages accelerates the algorithm's convergence to the minima.. 

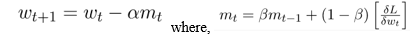
b. Root Mean Square Propagation (RMSP):  RMSprop, or root mean square prop, is an adaptive learning approach for improving AdaGrad. It uses the 'exponential moving average' instead of the cumulative sum of squared gradients, like AdaGrad does.

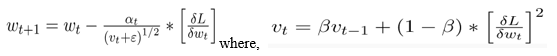
The strengths or good features of the aforementioned two approaches are inherited by Adam Optimizer, which builds on them to provide a better efficient gradient descent.

Adam Optimizer's Mathematical Aspects:

Using the formulae from the previous two ways,

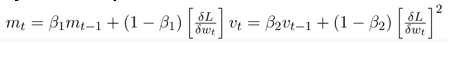
C. Training the DTLN model using tf dataset

D. Test the Model

1) Read an audio file, network-process it, and save the upgraded audio as a.wav file.

2) Find.wav files in the "folder name" folder and subfolders, apply an algorithm to each.wav file, and save it to disc in the "new folder name" folder. The original directory's structure has been maintained. The files that have been processed will be stored under the same name as the original file.

Conclusion

This paper described a noise suppression method based on a stacked dual signal transformation LSTM network for real-time speech enhancement that had been trained on a large data set. In a stacked network approach, we were able to demonstrate the benefit of using two types of analysis and synthesis bases.

References

[1] Davit Baghdasaryan, Real-Time Noise Suppression Using Deep Learning, Towards Data Science, Dec. 2018. [2] Salih, A. (2017) Audio Noise Reduction Using Low Pass Filters. Open Access Library Journal, 4, 1-7. doi: 10.4236/oalib.1103709. [3] Strake, M., Defraene, B., Fluyt, K., Tirry, W., & Fingscheidt, T. (2019). Separated Noise Suppression and Speech Restoration: Lstm-Based Speech Enhancement in Two Stages. 2019 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA). doi:10.1109/waspaa.2019.8937222 [4] Maximilian Strake, Bruno Defraene, Kristoff Fluyt, Wouter Tirry & Tim Fingscheidt, Speech enhancement by LSTM-based noise suppression followed by CNN-based speech restoration, EURASIP Journal on Advances in Signal Processing volume 2020 [5] Nils L. Westhausen, Bernd T. Meyer, “Dual-Signal Transformation LSTM Network for Real-Time Noise Suppression”, Oct 2020. arXiv:2005.07551 [6] Liu, M., Wang, Y., Wang, J., Wang, J., & Xie, X. (2018). Speech Enhancement Method Based On LSTM Neural Network for Speech Recognition. 2018 14th IEEE International Conference on Signal Processing (ICSP). doi:10.1109/icsp.2018.8652331 [7] Y. Xu, J. Du, L.-R. Dai, and C.-H. Lee, “An experimental study on speech enhancement based on deep neural networks,” IEEE Signal processing letters, vol. 21, no. 1, pp. 65–68, 2013. [8] S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural computation, vol. 9, no. 8, pp. 1735–1780, 1997. [9] S. R. Park and J. Lee, “A fully convolutional neural network for speech enhancement,” arXiv preprint arXiv:1609.07132, 2016. [10] J. L. Ba, J. R. Kiros, and G. E. Hinton, “Layer normalization,” arXiv preprint arXiv:1607.06450, 2016.

Copyright

Copyright © 2022 W. Shivani Patnaik, Telukuntla Sharath Kumar , Singam Chandana Reddy , P. Sreedhar, Dr. K. Kranthi Kumar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.