Comparison between Multi Epipolar Geometry & Affine 2d Transformation-Based Filters for Optical Robot Navigation

Abstract

In previous research papers, Multi Epipolar Geometry-based Filter (M-EGF) has proven its high capability to overcome Single Epipolar Geometry-based Filter (S-EGF) as well as with conformal 2D Transformation-based Filter (C-2DF) in terms of providing precise, trusted, outlier-free, and real time Automatic Image Matching (AIM) results for Optical Robot Navigation (ORN) applications. This paper comes in a series of comparing M-EGF with the most common filters extensively used in ORN. Affine 2D Transformation-based Filter (A-2DF) is another familiar filter used for detecting outliers in AIM results and regards as the advanced version of C-2DF, where it can deal with any changing or distortion in image scales in X and Y directions. In this paper, M-EGF has been compared with A-2DF using the same system, tests, tracks and images and the same evaluation techniques used for comparing M-EGF to S-EGF and C-2DF in the related research papers. Tests show that A-2DF is similar to C-2DF in terms of its disability to filter AIM results in areas with open, narrow, and confused Depth Of Field (DOF). A-2DF is also limited in terms of finding out the 6 correct parameters for its mathematical model when AIM results includes a significant number of mismatching points. Difficult view angles has also a noted effect on the performance of A-2DF, but less than that of C-2DF due to its ability to work with different scales. In tests including limited DOF and low level of outliers, A-2DF has shown comparatively adequate outcomes, that is suitable for non-sensitive applications, in which the error does not entail any serious consequences. A-2DF is independent of the errors in Exterior Orientation Parameters (EOP) and Interior Orientation Elements (IOE) of cameras, where it is image points dependent estimation filter. Tests show that M-EGF is time- effective, efficient with any AIM findings, regardless DOF, capturing angle, outliers rate in observations, type of features and tracks. Unlike, A-2DF, tests show that the performance of M-EGF can affect by the quality of IOEs and EOPs, as a number of correctly matched points might be rejected, and this limitation is not related to the filter mathematical design but the professionalism of cameras calibration and EOP determination. in terms of processing time, A-2DF is considerably slow comparing with M-EGF due to its iterative and repeatability design, which makes it, unlike M-EGF, unsuitable for real-time precise ORN applications.

Introduction

I. INTRODUCTION

These days, ORN method is used in many applications, including security, medical and engineering subjects for measuring the relative displacement in positioning and changes in orientation [1]. ORN uses the surrounding features for localization and, when the robot moves, ORN uses these navigation data for mapping the new surroundings, which will be used for the new localization and so on [2]. In ORN method, navigation is based on extracting reliable physical targets from captured images using analytical photogrammetry [3], and this art is a part of information technology discipline known as geomatics engineering [4]. Co-linearity and co-planarity equations are the main mathematical relationships used for linking the main parameters used in ORN, including camera IOPs,  and EOPs, coordinates image points, Ground Control Points (GCP), and Object Space Coordinate (OSC) [1, 2]. Different photogrammetric solutions can be obtained by these two types of equations in both relative and kinematic cases, including Space Resection (SR), Space Intersection (SI), Bundle Block Adjustment (BBA), and Self-Calibration Bundle Block Adjustment (SCBBA) [2], [3]. There are two main parts in ORN, namely the mathematical calculations that are based on clear functions and relationships, and intelligent part, which is based on vision applications [1], [4]. Using visual devices, ORN is known as vision or image-based navigation, and using laser scanning devices, it is known as laser-based navigation. The other term that is used for ORN is Simultaneous Localization And Mapping (SLAM), which is commonly used in computer sciences and artificial intelligence [4]-[6].

A number of research papers address different techniques for ORN, which different according to the involved mission, application type, neighboring atmosphere, and results quality [1], [4]. Examples of the other navigation techniques are low-cost GPS receivers [7], integration of low-cost GPS/INS [8], integration of GPS/delta positioning [9] and GPS delta positioning/MEMS-based INS integration [10], [11]. This interest and focus on the techniques of ORN is a clear reflection of the intense competition from companies and the growing demand in the labor market for such applications, which are now used in all fields.

Finding the identical points in the overlapping area between the two images used by robots is the key point behind successful ORN. Several methods are currently used by artificial intelligence for AIM, which are in general based on matching areas, features or relation using cross and Least Squares Method (LSM) correlation techniques. The most frequently used techniques used in AIM applications are Scale Invariant Feature Transform (SIFT) [12], Speeded Up Robust Features (SURF) [13], Principal Component Analysis (PCA)–SIFT, which have been studied, adjusted and compared to each other extensively and used for various applications [14]-[17].

As the successful AIM is the key behind the ideal ORN, detecting wrongly matched image points is the main step for precise and consistent outputs, and the more outliers in the results, the more degraded and distorted navigation, and at a specific point, the navigation solution may not be possible. in ORN, observations are single quantity, thus it is not possible to use the theory of errors for detecting gross errors during a LSM [1]. Several methods are used for dealing with outliers in AIM, which generally can be grouped to image points-independent/dependent models. In outliers detection methods that are based on points-independent models, the mathematical model with its all parameters are identified with flexibility ranges, and the results AIM techniques are checked directly in the model without any estimation steps. Examples of the mathematical models used in such techniques are the co-linearity and co-planarity conditions. S-EGF and M-EGF, introduced, investigated, and studied by the author in [1], [2], [4], [5] are examples on filters based on image points-independent models. 2D conformal and affine transformation methods and examples of image points-dependent models, where the mathematical models are known, whereas all parameters are unknown and should be estimated firstly based on the observations that are required to be filtered. The two types of filters are used in ORN each one has its advantages and limitations, and suitable for specific applications and uses [1], [4]. Random Sample Consensus (RANSAC) is one of the main techniques that can be with used with the second type of filtration techniques that based on image point dependent models. RUNSAC can be used for estimating the parameters of 2D affine and conformal transformation from a set of matched image points even though  including outliers. The first step in RANSAC is to use the lowest essential number of random image points, wanted for defining the required parameters. No statistical information can be obtained in this step as no redundancies are available in the achieved solution. Then the obtained mathematical model is used for checking the rest of image points and classified the observations into fitted and outliers. The model returns back to the outliers group and uses another minimum number of points to get another set of parameters, which are used after that for classifying the rest of data as in the previous stages. This procedure is continued until the rest of remaining data are less than the minimum requirements for determining another mathematical model. The model that includes the biggest number of fitted points is regarded as the fit solution and all the data not fitted to this model are considered as outliers. RANSAC tends to be effective with data including a sensible number of gross errors in the observations, and with increasing the rate of outliers, the opportunity of determining the accurate model decreases. Increasing the number of iterations can help to detect the best fit solution, but on the other hand, increasing the processing time and making the technique as time consuming. Conversely, decreasing the number of iterations can affect the quality of the obtained solution, and with significant number of outliers and low number of iterations, the right model possibly will not be reached. The need of threshold values is regarded as another disadvantage of RANSAC, where they are required to be correctly judged. These values play a significant role in helping the model to be flexible enough to not reject data when it should be accepted and vice versa. Giving more flexibility for the model than that required can help to include all the right matching points with a small number of gross errors, which can be filtered after that using simple outliers detection techniques, such as Data Spoofing Method, based on LSM statistical testing indications [1], [2],[ 4]. This paper is part of a series of studies including the comparison of M-EGF with different types of AIM filters. In this paper, M-EGF and A-2DF are compared to each other, evaluated and tested. The two filters are fall under different design ideas, where M-EGF is an image points-independent model that is based on photogrammetric co-planarity conditions, whereas A-2DF is an image points-dependent model that is based on 2D affine transformation equations. The same ORN system with the same tests, images, trajectories, and evaluation techniques used in [1], [4], has also been for assessing and examining the two filters in various AIM atmospheres, including several levels of DOF, different capturing and vision angles, type matching features, and level of outliers in image points. The EOPs and IOEs of the three cameras used in the system are the same of that used in [1], [4], which have been determined strictly using Australis Software with automatic coded targets. The performance of M-EGF and A-2DF is assessed according to the number of wrongly rejected and accepted points.

II. THE MATHEMATICAL DESCRIPTION

A. 2D Affine Transformation-Based Filter (A-2DF)

2D affine transformation is the advanced version of 2D conformal transformation, where it can deal with 2 different scales, and compensate for non-perpendicularity of the axis system. 2D affine transformation includes two additional parameters to the four parameters used in conformal transformation, namely: 2 scales in X & Y directions, correction for non-perpendicularity, rotation angle, and 2D displacements. As a minimum, 3 points must be known in both arbitrary and final coordinate systems to apply 2D affine transformation model and determining the required 6 unknowns. 2D Affine transformation is expected to work well with AIM, where scales of figures in images tend to be affected with view angles as well as DOF. For robust geometry and reliable results, as much points as possible should be processed using LSM to determine the 6 required parameters, which can help to provide valuable statistical testing indications for identifying and eliminating gross errors in observations. Moreover, the well distribution of the points across the images helps to provide robust geometry and decreased the number of rejected points. In ORN, A-2DF is applied using RUNSAC and followed by LSM, the mathematical model of A-2DF for any number of points (n) are illustrated below:

1. RUNSAC: Choosing 3 arbitrary points in image (1) and there matching points in image (2) as the lowest number of observations used for getting the 6 parameters of A-2DF. Equations (1.1 to 1.12) show the mathematical model of 2D conformal transformation:

E(A) = a0 + a1 * X(A) + a2 * Y(A)                                              (1.1)

N(A) = b0 + b1 * Y(A) + b2 * Y(A)                                              (1.2)

E(B) = a0 + a1 * X(B) + a2 * Y(B)                                              (1.3)

N(B) = b0 + b1 * Y(B) + b2 * Y(B)                                              (1.4)

E(C) = a0 + a1 * X(C) + a2 * Y(C)                                              (1.5)

N(C) = b0 + b1 * Y(C) + b2 * Y(C)                                              (1.6)

Where,                                                      

α = tan-1 (-a2 / b2)                                                                   (1.7)

ε  = tan-1 (-b1 / a1) + α                                                            (1.8)

SX = a1 * (cos (ε) / cos (ε – α))                                               (1.9)

SY = b2 * (cos (ε) / cos (α))                                                    (1.10)

T(E) = a0                                                                                   (1.11)

T(N) = b0                                                                                   (1.12)

And,

T(E), T(N)                                       Displacement parameters of 2D affine transformation

SX, SY                                           Scale changing in X & Y directions

α                                                  Rotation angle

ε                                                   Nonorthogonality correction

X(A),Y(A) ,..., …., X(C), Y(C)            The coordinates of points (A), (B) & (C) in X-Y coordinate system

E(A),N(A) ,..., ...., E(C), N(C)           The coordinates of points (A), (B) & (C) in E-N coordinate system

2. RUNSAC: Applying A-2DF with the determined parameters on all matched points, finding out the observations that applicable and non-applicable to the model taking into account the allowable boundaries.

3. RUNSAC: Another 3 points are selected subjectively from the non-applicable points gotten in step (2) and used again to determine new 6 parameters of the same model, and applied again for the rest of points, and so on. These steps continue until the remaining number of non-applicable points become less than 3 points. The 6 parameters that fitted the highest number points is used as the correct model and the rest as outliers.

4. LSM: As RUNSAC results obtained from the previous steps are expected to contain outliers due to the threshold values used for providing the model with reasonable flexibility to not reject the correctly matched points; thus, LSM is applied for the RUNSAC results to determine the model parameters and computing the residuals and the standard deviation of each observation from the covariance matrix of residuals. Equations (2.1 to 2.8) show example of A-2DF equations with redundancy and residuals are included to make them consistent:

E(A) + VE(A)  = a0 + a1 * X(A) + a2 * Y(A)                                 (2.1)

N(A) + VN(A) = b0 + b1 * X(A) + b2 * Y(A)                                 (2.2)

E(B) + VE(B)  = a0 + a1 * X(B) + a2 * Y(B)                                 (2.3)

N(B) + VN(B) = b0 + b1 * X(B) + b2 * Y(B)                                 (2.4)

E(C) + VE(C)  = a0 + a1 * X(C) + a2 * Y(C)                                (2.5)

N(C) + VN(C) = b0 + b1 * X(C) + b2 * Y(C)                                 (2.6)

E(n) + VE(n)  =  a0 + a1 * X(n) + a2 * Y(n)                                  (2.7)

N(n) + VN(n) =  b0 + b1 * X(n) + b2 * Y(n)                                 (2.8)

Where,

a0, b0                                                          As in Equations. (1.11 to 1.12)       

X(A) , Y(A) , ……X(n) , Y(n)                             The most probable computed values (error-free values)

E(A) , N(A) , ……E(n) , N(n)                            Observed values including errors

VE(A), VN(A) ,……. VE(n), VN(n)                       Residuals in observations

As the errors are not limited for one image and free in the other image, and also, as it is not possible to use observation equations  with more than one observation in each equation, additional equations including the rest of observations with their observed value and the most probable values have been used and shown below:

XO(A) + V(Xo(A)) = X(A)                                                      (2.9)

YO(A) + V(Yo(A)) =   Y(A)                                                      (2.10)

XO(B) + V(Xo(B)) = X(B)                                                      (2.11)

YO(B) + V(Yo(B)) =   Y(B)                                                      (2.12)

XO(C) + V(Xo(C))  = X(C)                                                      (2.13)

YO(C) + V(Yo(C))  = Y(C)                                                      (2.14)

XO(n) + V(Xo(n))  = X(n)                                                      (2.15)

YO(n) + V(Yo(n))  = Y(n)                                                      (2.16)

Where,

XO(A) , YO(A) , ……, XO(n) , YO(n)                          Observed values including errors

X (A) , Y (A) , ……, X (n) , Y (n)                               Error-free values

V(Xo(A)) , V(Yo(A)) , ……,. V(Xo(n)) , V(Yo(n))             Residuals

These equations can be solved using LSM, providing useful statistical testing information. All Equations shown above can be arranged in LSM matrixes of as follows, and solved as shown:

A(n * m) * X(m *1) = L(n *1) + V(n *1)                                                                                                                (3)

X(m *1) = (AT(m * n) * W(n * n) * A(n * m))-1 * (AT(m * n) * W(n * n) * L(n *1))                                                         (4)

Where,

n                                           The number of all observations

m                                          The number of unknowns

A                                           Matrix of coefficients

AT                                         Matrix transpose

W                                          Matrix of observations weights

X                                           Matrix of unknowns

L                                           Matrix of constant terms

V                                           Matrix of residuals

A =      1X(A)Y(A)000000000….000001X(A)Y(A)000000….001X(B)Y(B)000000000….000001X(B)Y(B)000000….001X(C)Y(C)000000000….000001X(C)Y(C)000000….00….….….….….….….….….….….….….001X(n)Y(n)000000000….000001X(n)Y(n)000000….00000000100000….00000000010000….00000000001000….00000000000100….00000000000010….00000000000001….00….….….….….….….….….….….….….00000000000000010000000000000001                (5)

W =  unite matrix with diagonal of weight value of each observation:

[wX(A) ; wY(A) ; wX(B) ;  wY(B) ;  wX(C) ; wY(C) ; ……. ..….; wX(n) ; wY(n) ; wXO(A) ; wYO(A) ; wXO(B) ; wYO(B) ; wXO(C) ; wYO(C) ;  ..…...…..; wXO(n) ; wYO(n)]                                                                                                                                          (6)             

X = Vector matrix with one column of unknowns, including the 6 transformation parameters and the "true" values of X-Y system observations:

[a0 ; a1 ; a2 ; b0 ; b1 ; b2 ; T(N); T(E) ; X(A) ; Y(A) ; X(B) ; Y(B) ; X(C) ; Y(C) ; ……..…..; X(n) ; Y(n)]                              (7)

L = Vector matrix with one column of:

[E(A) ; N(A) ; E(B) ; N(B) ; E(C) ; N(C) ; …….…..; E(n) ; N(n) ; XO(A) ; YO(A) ; XO(B) ; YO(B) ; XO(C) ; YO(C)  …….…..; XO(n) ; YO(n)]        (8)

 V = Vector matrix with one column of observations:

[VE(A) ; VN(A) ; VE(B) ; VN(B) ; VE(C) ; VN(C) ;…….…..; VE(n) ; VN(n) ; V(Xo(A)) ; V(Yo(A)) ; V(Xo(B)) ; V(Yo(B)) ; V(Xo(C)) ; V(Yo(C))  …….….; V(Xo(n)) ; V(Yo(n))]                                                                                                                                                                            (9)

5. LSM: As the majority of outliers in observations have been eliminated using RUNSAC, the remain outliers can be detected using DSM or any comparable outliers, that are appropriate just for data including low rate of outliers. Firstly, LSM is used for determining the covariance matrix of observations, which is used from determining the standard deviation of the residual of each observation. The percentage between the residual and the value of standard deviation for each observation should < 3, providing confidence level of 99% confidence level with just 1% probability of rejection the couple of correctly matched points. After removing the detected outliers, all inlier observations are bundled again to calculate the final 6 unknowns, and the final fitted points are used directly in analytical photogrammetric solutions for ORN. Equations (11, 12, 13) show DSM equations used in to detect outliers form LSM results.

CQV(n * n) = W-1(n * n) - A(n * m) *  (AT (m* n) * W (n * n)  * A (n * m)) * AT (m * n)                                                                 (10)

The slandered deviation (StV (1: n)) of observation residuals from (1 to n) is the root square of the diagonal of matrix CQV(n * n):

StV. (1:n) = [StV. E(A) ;  StV. N(A) ;  StV. E(B) ;  StV. N(B) ; StV. E(C) ;  StV. N(C) ;…….…..;  StV. E(n) ;  StV. N(n) ;  StV. (Xo(A)) ;  StV. (Yo(A)) ;  StV. (Xo(B)) ;  StV. (Yo(B)) ; StV. (Xo(C)) ;  StV. (Yo(C)) ; …….…..; StV. (Xo(n)) ;  StV. (Yo(n))]                                                                                   (11)

w =  [VE(A)/StV. E(A) ;  VN(A)/StV. N(A) ;  VE(B)/StV. E(B) ;  VN(B)/StV. N(B) ; VE(C)/StV. E(C) ;  VN(C)/StV. N(C) ;…….…..; VE(n)/StV. E(n) ; VN(n)/StV.N(n) ; V(Xo(A))/StV. (Xo(A)) ; V(Yo(A))/ StV. (Yo(A)) ; V(Xo(B))/ StV. (Xo(B)) ; V(Yo(B))/ StV. (Yo(B)) ; V(Xo(C))/StV. (Xo(C)) ; V(Yo(C))/StV. (Yo(C)) ;….…..; V(Xo(n))/StV. (Xo(n)) ; V(Yo(n))/StV. (Yo(n))]                                                                                                                                             (12)

B. Multi-Epipolar Geometry-Based Filter (M-EGF)

As M-EGF has been introduced, explained, investigated and studied by the author in [1, 3, 4], just a brief description will be illustrated in this section with the mathematical model, and the reader is referred to [1, 3, 4] for more details. In brief, the idea of this filter is based on employing three cameras instead of two for filtering the AIM results, where 3 co-planarity conditions and 3 epipolar geometries will be formed as shown in figure (1). The three co-planarity equations can be written as following [1]:

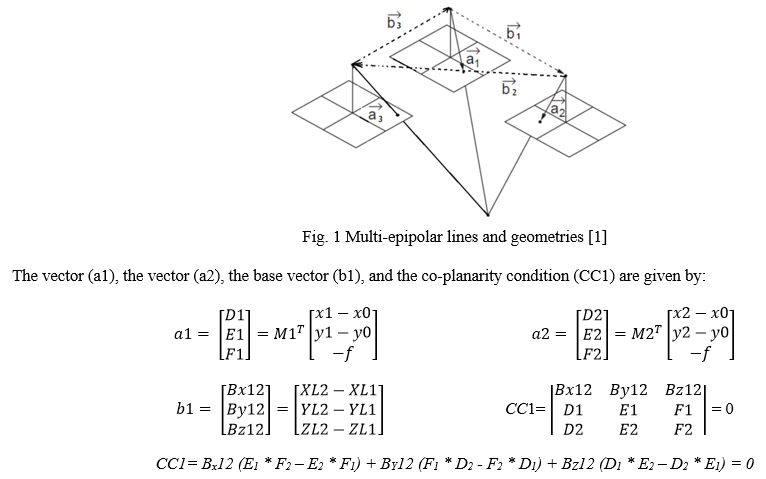
Where,

M1, M2, M3          The rotation matrix of the third image to be corresponding to the reference coordinate system, and in case of relative orientation, rotations in the first matrix are used as zeros and relative values are used for the rotations of the second and third images.

x1, x2, x3                The "x" image coordinates of the same object on the three images.

y1, y2, y3                The "y" image coordinates of the same object on the three images.

XL1, YL1, ZL1             The coordinates of the first capturing station

XL2, YL2, ZL2          The coordinates of the second capturing station

XL3, YL3, ZL3          The coordinates of the third capturing station

f, x0, y0                  The camera IOEs (focal length and the coordinates of camera optical centre on the image).

 As the EOPs and IOEs of the three cameras are known with certain standard deviation values, the 3 co-planarity condition equations between each two images are applied. Passing the 3 matched points from these 3 co-planarity conditions proven that these set of points is inlier and correctly matched. As shown in figure (2), M-EGF consists of 3 S-EGF, each one has the ability to detect any outliers between the two related images, except those located on epipolar plane. Therefore, the probability of outliers to move through the 3 filters is almost zero.

III. TESTING, RESULTS & DISCUSSION

The two filters have been tested in different AIM environments with the same system, pictures, trajectories, and EOPs & IOEs used for comparing M-EGF with S-EGF and C-2DF in [1] and [4]. Figures (2), (3), and (4) show examples of AIM environments and examples on undetected mismatched points for A-2DF.

The evaluation technique used in this paper is similar to that followed in [1] and [4], which can be summarized as following:

A-2DF has been developed in Matlab using RANSAC and LSM to estimate the 6 parameters of the mathematical model, removing the outliers as explained in section (2.1). The mathematical model of M-EGF has also been developed in Matlab, supporting with the values of EOPs & IOEs of the three cameras, and some statistical thresholds, giving the final passed points. The inputs of the two filters are the AIM points that results from adjusted SURF algorithm. See [2] for more information. Using just the best 100 matched pints between each three images, a total of 2700 automatic matched points, distributed on 27 pictures, taken by 3 cameras in 9 synchronised captured processing are used for each filter. These points have been manually checked and classified as inliers and outliers for precise evaluation. The error percentage of the accepted points that should be rejected (E%-AC), and the rejected points that should be accepted (E%-RJ) are used for comparing the performing of the two filters. Table (2) illustrates (E%-AC) and (E%-RJ) of M-EGF and A-2DF.

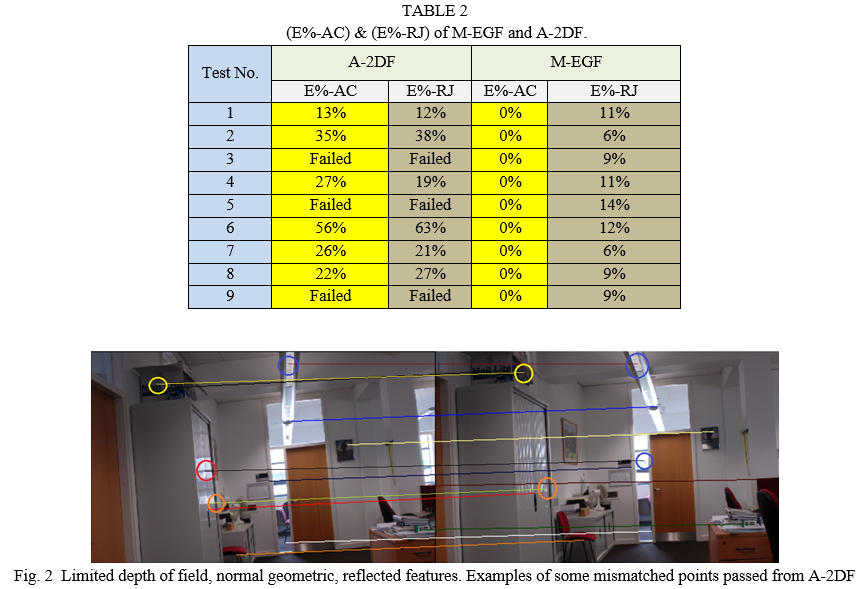
As clear from table (1) and table (2), A-2DF is disable to deal with AIM results of in areas with open, narrow, and confused DOF. This reflects the disability of RUNSAC and LSM of extracting the correct 6 parameters of 2D transformation, which can be referred to increasing the number of outliers in SURF results. DOF is an expected reason behind the high rate of outliers, where relationships between the points on the two images can change drastically. A-2DF has shown healthy results in areas with limited DOF, where the connections between points in the two images is almost invariable and the 6 parameters can be easily estimated. With relatively difficult view of angle, A-2DF has shown acceptable results, which can be referred to the flexibility of the affine mathematical model to work with observation including different scales  Furthermore, A-2DF is considerably affected by the complexity of AIM environment, as it is completely based on estimating the correct mathematical model form the results of AIM techniques. The other disadvantage of A-2DF is the long processing time spent for estimating the 6 parameters of the mathematical model, as RUNSAC and LSM are based on iteration and depend on utilizing statistical testing for achieving the final fit results. This feature keeps A-2DF away from being used with real time ORN applications. On the other side of comparison, M-EGF has shown a great power to work with all type of AIM results taking from ass different environments illustrated in table (1), apart from all effective factors that can influence the performance of AIM, such as gross errors rates, DOF, view angles, type of trajectory, type of matching features, and so on. This can be attributed to the fact that M-EGF is an image points independent filter, so no need for estimating any mathematical parameters. Also, M-EGF depends on a clear mathematical model with nearly fixed values, so extracting the outliers in observations is a matter of applications. It should be noted that some flexibility is required for the EOPs and IOEs of the 3 cameras used in the system for the filter to be not very strict and, as a result, rejects correctly matched points when they should be accepted. However, as illustrated in table (2), even with these flexibility values used, M-EGF has E%-RJ, which can be attributed to the quality of manufacturing the system from a side, and to the quality of the cameras used from the other side. As for the system, it is not perfectly manufactured, where it has been just made by simple potentials, and the small movements of the cameras in positioning and rotations are highly expected. In term of the cameras, they are non-metric cameras with relatively unstable IOEs, which can affect the performance of the filter by changing the co-linearity condition parameters. Figure (4) is a clear example of the high ability of M-EGF for dealing with difficult capturing view and different DOP, where the possibility of passing the 3 epipolar geometric conditions is nearly zero. Results show that M-EGF is time effective, efficient, trusted, and reliable, which make it suitable for real time, precise and critical ORN applications.   

Conclusion

In this paper, M-EGF and A-2DF have been tested, evaluated and compared to each other. Specific system that simulating ORN has been used in this comparison and used in different AIM environments, including different DOF, viewing angles, type of trajectories, and type of matching features. The two filters have been assessed with 27 images, each 3 are synchronized, with the best 100 matching points in each image obtained by SURF. Results show that A-2DF have failed to deal with SURF results environments with open, narrow, and confused DOF due to the confused relationships between the figures in the matched images. Also, A-2DF have failed to determine the 6 parameters and the exact mathematical model using the best SURF results with high rate of gross errors due to capturing images by difficult view angles. With limited DOF and normal view of angle, the number of outliers in SURF results has been reasonable, and the relationship between the matching points in the two images has been normal, thus A-2DF has shown sufficient results, which can be used for imprecise ORN applications. The processing time of A-2DF is relatively long, due to the main depending on iteration estimation techniques, namely LSM and RUNSAC, making the filter is unsuitable for real time and fast applications. Tests show that M-EGF are streamlined, effective, and quick with large proficiency to deal with all SURF results, not considering DOF, view angles, type of trajectory, type of matching features, and the percentage of gross errors in observations. the quality of EOPs and IOEs used in the mathematical model of M-EGF has a noted effect on the performance of the filter, leading to rejection a number of identical points that should be accepted. Tests have reflected the high opportunity of M-EGF to be used precise, reliable, and real time ORN applications.

References

[1] M. M. Amami, “Comparison Between Multi & Single Epipolar Geometry-Based Filters for Optical Robot Navigation,” International Research Journal of Modernization in Engineering Technology and Science, vol. 4, issue 3, March. 2022. [2] M. M. Amami, “Low-Cost Vision-Based Personal Mobile Mapping System,” PhD thesis, University of Nottingham, UK. 2015. [3] McGlone, J. C., Mikhail, E. M., Bethel, J. and Roy, M. Manual of photogrammetry. 5th ed. Bethesda, Md.: American Society of Photogrammetry and Remote Sensing. 2004. [4] M. M. Amami, “Comparison Between Multi Epipolar Geometry & Conformal 2D Transformation-Based Filters for Optical Robot Navigation,” International Journal for Research in Applied Sciences and Engineering Technology, vol. 10, issue 3, March. 2022. [5] M. M. Amami, M. J. Smith, and N. Kokkas, “Low Cost Vision Based Personal Mobile Mapping System,” ISPRS- International Archives of The Photogrammetry, Remote Sensing and Spatial Information Sciences, XL-3/W1, pp. 1-6. 2014 [6] Bayoud, F. A. Development of a Robotic Mobile Mapping System by Vision-Aided Inertial Navigation: A Geomatics Approach. [Doctoral dissertation]. University of Calgary, Canada. 2006. [7] M. M. Amami, “Testing Patch, Helix and Vertical Dipole GPS Antennas with/without Choke Ring Frame,” International Journal for Research in Applied Sciences and Engineering Technology, vol. 10, issue 2, pp. 933-938, Feb. 2022. [8] M. M. Amami, “The Advantages and Limitations of Low-Cost Single Frequency GPS/MEMS-Based INS Integration,” Global Journal of Engineering and Technology Advances, vol. 10, pp. 018-031, Feb. 2022. [9] M. M. Amami, “Enhancing Stand-Alone GPS Code Positioning Using Stand-Alone Double Differencing Carrier Phase Relative Positioning,” Journal of Duhok University (Pure and Eng. Sciences), vol. 20, pp. 347-355, July. 2017. [10] M. M. Amami, “The Integration of Time-Based Single Frequency Double Differencing Carrier Phase GPS / Micro-Elctromechanical System-Based INS,” International Journal of Recent Advances and technology, vol. 5, pp. 43-56. Dec. 2018. [11] M. M. Amami, “The Integration of Stand-Alone GPS Code Positioning, Carrier Phase Delta Positioning & MEMS-Based INS,” International Research Journal of Modernization in Engineering Technology and Science, vol. 4, issue 3, March. 2022. [12] Lowe, D. Distinctive Image Features from Scale-Invariant Key points, IJCV. 2004; 60(2):91–110. [13] Bay, H,. Tuytelaars, T., and Van Gool, L. SURF: Speeded Up Robust Features. 9th European Conference on Computer Vision. 2006. [14] Juan, L. and Gwun, O. A comparison of SIFT, PCA-SIFT and SURF. International Journal of Image Processing (IJIP).; vol. 3, pp. 143-152. 2009 [15] Panchal, P. M., Panchal, S. R., and Shah, S. K. A Comparison of SIFT and SURF. International Journal of Innovative Research In Computer And Communication Engineering, vol. 1(2), pp. 323-327. 2013 [16] M. M. Amami, “Speeding up SIFT, PCA-SIFT & SURF Using Image Pyramid,” Journal of Duhok University, [S.I], vol. 20, July. 2017. [17] M. M. Amami, “Fast and Reliable Vision-Based Navigation for Real Time Kinematic Applications,” International Journal for Research in Applied Sciences and Engineering Technology, vol. 10, issue 2, pp. 922-932, Feb. 2022.

Copyright

Copyright © 2022 Mustafa M. Amami. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.