Computational Analysis of Erosion Wear Rate by Multiphase Flow in Optimum Bend Ratio of Pipeline

Abstract

: Pipe bends are an integral part of transportation system as they help by providing flexibility in the path. In this paper, flow of mono-dispersed particles with carrier flow is simulated using Computational Fluid Dynamics by implementing Eulerian two-phase model in FLUENT. This paper is a forward stepping stone as it depicts the effect of pipeline bend on flow characteristic such as erosion rate, concentration profile, wall shear stress, etc. after numerous researches on pressure drop and velocity profiles. In this paper, a two-phase fluid of silica sand, having mean diameter of 450 µm (density = 2650 kg/m3), and water are mixed at the ratio of 8.82% solid concentration by weight and flown through a pipeline with diameter 53.0 mm and the optimum pipe bend ratio of 5.60 for minimum pressure loss.

Introduction

I. INTRODUCTION

Erosion is an unavoidable phenomenon in the pipelines transporting bulk solids in both hydraulic and pneumatic conveying modes. Erosion wear is influenced by a variety of elements such as material hardness, solid particle size and shape, solid concentration, particle velocity, solid impact angle on the target material surface, and so on.

Several investigators have made systematic studies to establish the functional dependence of erosion wear on various parameters. Bahadur and Badruddin [1], Gandhi et al. [2], Singh et al. [3] investigated on how characteristics such as solid concentration, flow velocity and particle size in coal-water slurry influenced the erosion wear. Deng et al. [4] and Heilbronner et al. [5] studied the effect of size, shape and rotation of the particles on erosion. They concluded that irregular particles had a stronger influence on erosion than spherical particles.

Though the number of affecting factors are numerous with each having an independent influence on erosion, Gupta et al. [6] managed to create a relationship, an empirical formula, which has been preferred by many academics to estimate erosion rates. The equation is as expressed below:

where ER  is erosion rate, V  is the speed of rotation, d  is the average diameter of particles, C is the slurry concentration (% by wt.) and a, x, y, z  are constants depending on the process of erosion and material properties

In case of translatory motion, rotational velocity is replaced by mean velocity [7-9]. Other factors that affect erosion-corrosion in slurry pipelines but not included in the above equation for computational convenience include pH, effect of usage of additive layers on inner walls of pipelines, geometry of pipelines, etc. Hessari and Round [10], Singh et al. [11] and Kaushal et al. [12] investigated the influenced of pH value on erosion in stainless steel pipelines.  

Pipe bends, elbows, expansion-contraction, etc. are also an important component of any pipeline network since they allow for routing flexibility. However, there have been limited studies on bends for solid–liquid two-phase flow. Some of the prominent results in this domain are listed below in Table 1.

Table 1: Researchers and their contribution to multiphase flow in pipe bends

Numerous studies have successfully concluded that a pipe bend ratio of 5-5.7 is the most convenient for minimum pressure drop across the bend [13, 18-19]. In this paper we have tried to simulate the flow of multiphase fluid in optimum bend ratio pipeline to find its effect on erosion and wall shear stress, thus enquiring the safety of pipeline.

II. MATHEMATICAL MODELING

A. CFD Modeling

Modeling of the fluid is undertaken using Computational Fluid Dynamics (CFD). ANSYS FLUENT R19.0 Academic Package was used for all the fluid simulation of this paper. In the CFD code, FLUENT employs a finite volume approach. This is a widely used approach that may be found in various CFD codes. The control volume is a defined zone where the governing equations are applied. Because they describe the conservation of mass, momentum, and energy over the control volume, these equations are known as conservation equations.

The selection of multiphase model in the simulation usually relies on the solid particles concentration. It is important to choose the most suitable model according to one’s requirement as it distinguishes the momentum transference. Keeping in consideration that slurries are not dilute fluids, mixture and Eulerian models are the most suitable models for the study. Under Eulerian model, non-granular model tend to preclude friction and inter-particle collisions. This is why granular Eulerian model seemed to be the best option to for this case. 

B. Eulerian Model

The Eulerian two-phase model assumes that the slurry flow consists of solid and fluid phases. These are different entities but they create a single continuum in Eulerian model, such that αf + αs = 1.0, where αf and αs are volumetric concentrations of fluid and solid phase, respectively. However, the conservation equations are fulfilled by each phase as an independent entity.

The forces considered to be acting on the fluid particles in the Eulerian Model include static pressure gradient, inertial forces caused by particle reciprocity, drag force caused by difference in velocities of solid and fluid phases, viscous force, and body force. Apart from the listed forces, Drew and Lahey suggested two more forces acting on fluid particles namely virtual mass force and lift force respectively [20].

The derivation of the governing equations associated with Eulerian model has been provided by Drew in detail [21]. And the above-mentioned forces and their actions on the slurry continuum have been explained in detail by Kaushal et al [19].

C. Turbulence Modeling

Spalding and Launder first proposed the k-? model in 1972 [22]. Post this; there have been numerous refinement and modifications on the model. Yakhot and Orszag [23] proposed an enhancement to the k-? model by employing the renormalization group (RNG) theory. The constants of standard k-? model are deduced empirically using the RNG theory. This ensures that k-? model need not be tweaked repeatedly based on the flow type to provide better and accurate predictions for changes in flow like flow separation and flow through curved geometry. This reduces the computational efforts by 10-15% [24].

D. Wall Effects

The gradient of quantities near the wall is significant, necessitating fine grids. This increases the cost of the calculation by making it more time-consuming, needing more memory and quicker computer processing, as well as increasing the complexity of the equations. By replacing the fine grids with a set of equations relating the calculated variables at near-wall cells with the equivalent quantities on the wall, a wall function, which is a collection of semiempirical formulas and functions, allows a cheaper calculation. For both liquid and solid phases, the wall function aids in the more precise estimation of near-wall shear stresses.

It was ensured that the FLUENT included a hybrid near-wall modeling; including both the rigorous and wall function methods. The former method was used for cases of fine mesh for areas of interest while the latter was applied to the remaining part of the pipe, thus distinguishing areas of interest from the rest of pipe. This procedure gives an understanding and a balance between computational efforts and modeling errors as a part of near wall effects.

E. Geometry Modeling

Backed by numerous researchers’ findings, as mentioned, a bend ratio with minimum pressure loss associated was chosen to characterize the bend. A pipe with internal diameter of 53.0 mm and bend curvature radius of 148.4 mm was used to study the effect of erosion, resulting in bend ratio of 5.60.

As far as, the velocity at the inlet was concerned, many researchers have managed to show that a little to no effect was seen on critical deposition velocity by changes in different parameters including efflux concentration [25-26]. For this particular setup, Kaushal et al. [19] had experimentally found the critical deposition velocity to be 1.50-1.55 m/s. Keeping the same in consideration, a much higher value of 3.56 m/s of initial inlet velocity condition was chosen.

It has been established that a minimum of 30-50 times the bend diameter is a requisite for establishment of well-developed turbulent flow in a pipe. Keeping the same in mind, a 6.5 m of straight upstream pipe was chosen. Similarly at least a length of 140D was used as the downstream length to ensure proper observation of flow characteristics and re-distribution of solids in the downstream length.

Since it is a horizontal bend, the pipe was laid in the XY plane and the origin point was the centre of the velocity inlet face. The initial velocity was directed in the positive-Y direction and the outlet of the bend was towards the negative-X direction. The Z plane was intersecting the pipe at mid plane.

GAMBIT software was used to generate the computational grid. It consisted of 3,890,258 cells and 4,503,654 nodes. The grid-independence tests were carried out ensuring that all other contributing parameters were constant for all the cases. The initial grid was refined by approximately quadrupling the number of cells from 894,774 cells to 3,890,258 cells and then doubling the same from 3,890,258 cells to 5,526,047 cells. There were no additional enhancements in the results in later case. Hence, the mesh consisting of 3,890,258 cells was considered optimum and suitable for simulation.

III. SIMULATION AND RESULTS

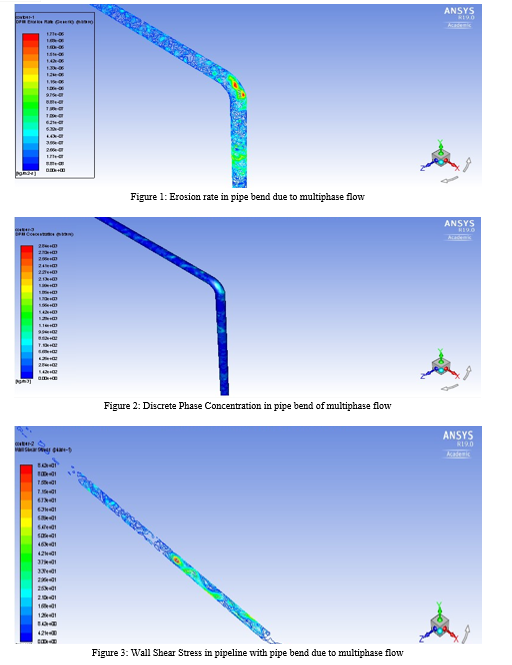
Silica sand (having density 2650 kg/m3) was used as the solid phase having mean diameter of 450 µm and mixed with carrier fluid water at a concentration of 8.82% by volume to simulate slow through the pipeline. A total of 700 iterations were required for convergence of the flow simulation with least count of 10-4 to check the effect of the flow on erosion, wall shear stress and particle distribution at the boundaries of the pipe wall was observed as shown in the following Figures 1-3.

Figure 1 shows the erosion rate map on the walls of the bend.

As expected, the erosion rate is maximum at the outer wall of the bend of the pipe due to vortex formation which aggravates the loss of material from the pipeline.

Numerically, the mean value of rate of erosion was observed to be 5.32 × 10-7 kg/m2-s. On converting the same into industrial rate of erosion, it was found to be approximately 5.17 mm/year.

And the highest value of erosion rate goes as high as 1.27 × 10-6 kg/m2-s, which when converted translates to 14.83 mm/year. This value is relatively almost double the value of erosion rate experienced by industries when compared, even if the slurry concentration is way less than the concentration at which industries operate. This value is subject to change as per the pipe material.

As suggested by many researchers before, apart from sudden pressure drop, the high rate of erosion at bend can also be explained by, the observation of solid particles to have been concentrated more near the walls at the pipe bend as shown in Figure 2.

Moreover, the maximum wall shear stress in the pipeline is observed to be in the downstream half of the pipe, approximately 2.5 m away from the bend outlet at 84 MPa.

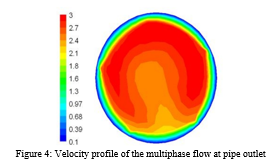
Figure 4 shows the velocity distribution at pipe outlet, which seemed to be typical turbulent flow pattern.

Conclusion

Based on the simulations conducted, the results suggest that the Eulerian model is quite effective to simulate two-phase flow in horizontal pipe bends. Apart from this some other conclusions based on this simulation includes: 1) The risk is higher to outer pipe bends walls due to aggressive erosion rate 2) Even if the solid concentration was lower, the erosion rate was observed to be twice the industrial erosion rate in straight pipelines 3) Higher solid concentration at walls near pipe bends must be one of the reasons for higher erosion rate 4) The velocity and concentration profile was observed to be unaffected by the pipe bend in upstream part of pipe 5) The solids were observed to be redistribution at downstream part of the bend. This could be due to secondary flows

References

[1] Bahadur, S. and Badruddin, R., 1990. Erodent particle characterization and the effect of particle size and shape on erosion. Wear, 138(1-2), pp.189-208. [2] Desale, G.R., Gandhi, B.K. and Jain, S.C., 2006. Effect of erodent properties on erosion wear of ductile type materials. Wear, 261(7-8), pp.914-921. [3] Singh, G., Kumar, S. and Sehgal, S.S., 2018. Taguchi approach to erosion wear optimization of WC-10Co-4Cr sprayed austenitic steel subjected to equisized slurry. Industrial Lubrication and Tribology. [4] Deng, T., Bingley, M.S. and Bradley, M.S., 2004. The influence of particle rotation on the solid particle erosion rate of metals. Wear, 256(11-12), pp.1037-1049. [5] Heilbronner, R. and Keulen, N., 2006. Grain size and grain shape analysis of fault rocks. Tectonophysics, 427(1-4), pp.199-216. [6] Gupta, R., Singh, S.N. and Sehadri, V., 1996. Prediction of uneven wear in a slurry pipeline on the basis of measurements in a pot tester. International Journal of Multiphase Flow, 22(S1), pp.152-152. [7] Desale, G.R., Gandhi, B.K. and Jain, S.C., 2006. Effect of erodent properties on erosion wear of ductile type materials. Wear, 261(7-8), pp.914-921. [8] Gupta, R., Singh, S.N. and Sehadri, V., 1995. Prediction of uneven wear in a slurry pipeline on the basis of measurements in a pot tester. Wear, 184(2), pp.169-178. [9] Kumar, R., Bhandari, S. and Goyal, A., 2017. Slurry erosion performance of high-velocity flame-sprayed Ni-20Al2O3 and Ni-10Al2O3-10TiO2 coatings under accelerated conditions. Journal of Thermal Spray Technology, 26(6), pp.1279-1291. [10] Round, G.F. and Hessari, A.R., 1987. Rheology of coal slurries, pH and size distribution effects. Particulate and Multiphase Processes, 3, pp.329-340. [11] Singh, M.K., Kumar, S. and Ratha, D., 2020. Computational analysis on disposal of coal slurry at high solid concentrations through slurry pipeline. International Journal of Coal Preparation and Utilization, 40(2), pp.116-130. [12] Singh, K.P., Kumar, A. and Kaushal, D.R., 2022. Experimental investigation on effects of solid concentration, chemical additives, and shear rate on the rheological properties of bottom ash (BA) slurry. International Journal of Coal Preparation and Utilization, 42(3), pp.609-622. [13] KALYANARAMAN, K. and AJ, R., 1973. CHARACTERISTICS OF SAND-WATER SLURRY IN 90OHORIZONTAL PIPE BENDS. [14] Turian, R.M., Ma, T.W., Hsu, F.L., Sung, M.J. and Plackmann, G.W., 1998. Flow of concentrated non-Newtonian slurries: 2. Friction losses in bends, fittings, valves and venturi meters. International journal of multiphase flow, 24(2), pp.243-269. [15] Bozzini, B., Ricotti, M.E., Boniardi, M. and Mele, C., 2003. Evaluation of erosion–corrosion in multiphase flow via CFD and experimental analysis. Wear, 255(1-6), pp.237-245. [16] Mansouri, A., Arabnejad, H., Shirazi, S.A. and McLaury, B.S., 2015. A combined CFD/experimental methodology for erosion prediction. Wear, 332, pp.1090-1097. [17] Njobuenwu, D.O. and Fairweather, M., 2012. Modelling of pipe bend erosion by dilute particle suspensions. Computers & Chemical Engineering, 42, pp.235-247. [18] Ito, H., 1960. Pressure losses in smooth pipe bends. [19] Kaushal, D.R., Kumar, A., Tomita, Y., Kuchii, S. and Tsukamoto, H., 2013. Flow of mono-dispersed particles through horizontal bend. International Journal of Multiphase Flow, 52, pp.71-91. [20] Drew, D.A., Lahey, R.T., 1993. Particulate Two – Phase Flow. Butterworth-Heinemann Publications, Boston, pp. 509–566. [21] Drew, D.A., 1982. Mathematical modeling of two-phase flow. WISCONSIN UNIV-MADISON MATHEMATICS RESEARCH CENTER. [22] Launder, B.E. and Spalding, D.B., 1972. Lectures in mathematical models of turbulence. [23] Yakhot, V. and Orszag, S.A., 1986. Renormalization group analysis of turbulence. I. Basic theory. Journal of scientific computing, 1(1), pp.3-51. [24] Choudhury, D., 1973. Introduction to the renormalization group method and turbulence modeling. Fluent incorporated. [25] Schaan, J., Sumner, R.J., Gillies, R.G. and Shook, C.A., 2000. The effect of particle shape on pipeline friction for Newtonian slurries of fine particles. The Canadian Journal of Chemical Engineering, 78(4), pp.717-725. [26] Kaushal, D.R. and Tomita, Y., 2002. Solids concentration profiles and pressure drop in pipeline flow of multisized particulate slurries. International journal of multiphase flow, 28(10), pp.1697-1717.

Copyright

Copyright © 2023 Sai Swapnesh Mishra, Kalpanta Mahapatra. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.