Design and Implementation of Pathfinding Algorithms in Unity 3D

Abstract

In this paper, the pathfinding algorithm has been implemented using Unity 3D. Unity-3D is a game engine that provides a 3D environment to statistically incorporate various multimedia data into one platform. It was developed by Unity Technology in the year 2005 and has become one of the most popular platforms for developing 2D and 3D games. The gaming environment provides several elements such as the PhysX physics engine, animation system, terrain editor, etc. Pathfinding is a dynamic process in which the plotting of the shortest path or route between two points is being determined by a computer application. Algorithms are defined as the steps required for completing a particular objective or a task.

Introduction

I. INTRODUCTION

Pathfinding is the searching technique for finding an optimal path from a starting location to a final(given) destination. The shortest-path problem is most studied in computer science. Generally, to represent the shortest path problem we use graphs. A graph is a visual depiction of a collection of things in which some objects are linked together by links. The interconnected objects are represented by points termed vertices and the edges are the ties that connect the vertices. An optimal shortest path is defined as the minimum length criteria from a source to a destination.

Pathfinding algorithm has become popular with the rise of gaming industries. Games with genres like survival, action-adventure, role-playing games, and real-time strategy games often have characters sent on missions from their current location to a predetermined destination. In these types of games, pathfinding algorithms have a dominant role. Some of the shortest path algorithms are namely as Dijkstra algorithm, Bellman-Ford algorithm, Floyd-Warshall algorithm, Genetic algorithm, A* pathfinding algorithm, etc.

Unity-3d is a game engine that is used by most of the gaming industries and indie game developers. This software is available for free which is one of the reasons for its high usage in the gaming industry. Unity-3d is a complete integrated development environment (IDE) with an asset workflow, scripting, integrated editor networking, scene builder, and more. It also includes a large community and forum where anyone interested in learning Unity can go and get answers to all of their questions. In unity-3D we use the c# programming language. Unity is a cross-platform developing software that is easy to learn for beginners and powerful enough for experts. 

II. OBJECTIVE

The main objective of this study is to understand and describe the how A*STAR pathfinding algorithm works using the software/engine Unity-3D.

Moreover, in this paper, we will also briefly discuss some of the other pathfinding algorithms. Since it is really necessary to understand the concept of pathfinding, we will also determine why A*STAR is the best pathfinding algorithm that exists today. We will even discuss how we are going to outline the following algorithm using Unity3D.

III. CONCEPT OF PATHFINDING

Pathfinding algorithms deal with the problem of determining a path from a source to a destination while avoiding obstacles and reducing expenditures (time, distance, risks, price, etc.). It is not an unusual location for a programming problem. We can see from navigation and gaming that the intermediate methods are useful for collective issues. It can assist in real-world issue solving, such as determining the shortest distance between our location and the nearest park. How can we find our way out of a maze? Is it possible to program a gaming character to find the exit while avoiding enemies? To begin our pathfinding investigation, we must first learn about BFS and DFS, as it is a crucial topic before pathfinding.

1. BFS (Breadth-First Search): Edward F. Moore published one of the two most essential graph traversal algorithms known as the Breadth-first search, in 1959.BFS explores equally in the directions until the goal is reached. Alternatively, we can say that it starts from a chosen node and examine its neighbor, the node which has been traversed is marked as visited. Breadth-?rst seeks is a graph traversal set of rules that begins of evolved by traversing the graph from the basis node and exploring all the neighboring nodes. Then, it selects the closest node and explores all the unexplored nodes. While the usage of BFS for traversal, any node within the side of the graph may be taken into consideration as the basis node. BFS uses a queue (FIFO). BFS guarantees the shortest path. The data structure used to represent the graph determines BFS's temporal complexity. The time complexity of the BFS algorithm is O (V+E), where V is the number of vertices, whereas E is the number of vertices. The space complexity is of BFS can be expressed as O (V).
2. DFS (Depth First Search): Depth-first search is the second fundamental graph traversal algorithm. DFS Traverses through exploring a way i.e. workable down every route earlier than going back. It is the purpose why you can additionally discover this set of rules beneath the call of Backtracking. Furthermore, this leads to a set of rules to apply for each iterative and recursive form. An approach for traversing or investigating data structures such as trees and graphs is known as a Depth-first search algorithm. The algorithm starts at the root node and proceeds down each branch as far as possible before returning to the root node. Depth First Search Traverses with the aid of exploring as some distance as feasibility down every course earlier than going back. It is the motive why you could additionally locate this set of rules the call of Backtracking. Furthermore, these belongings let in the set of rules to be carried out successfully in each iterative and recursive form. The algorithm begins its operation from the root node (or, in the case of a graph, selects any random node as the root node) and explores as far as possible down each branch before retracing. So the basic idea is to start at the root or any random node and mark it before going on to the next unmarked node and continuing the loop until there are no more unmarked nodes nearby. Then go back and look for more unmarked nodes to cross. Finally, print the nodes of the path

3. Dijkstra Algorithm: The Dijkstra algorithm determines the shortest path from the root node to the target node. Dijkstra is one of the most useful graph algorithms; it can also be simply altered to tackle a wide range of issues. Dijkstra's approach traverses the graph one vertex at a time, beginning with the object's origin. It next analyses the nearest vertex that is yet to be inspected, this procedure is repeated in an outer loop until either the vertex studied is the target or the target is not identified even after all vertices have been checked. Otherwise, the vertices that are closest to the inspected vertex are added to the collection of vertices to be studied. It spreads outwards from the initial place until it reaches the target. When the goal is identified, the loop gets terminated, and the algorithm returns to the beginning, remembering the needed path. The formula to determine the shortest path using the Dijkstra algorithm is:

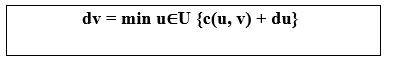
4. Greedy Best First Search Algorithm (Greedy Search): The greedy best-first search algorithm always selects the path that appears to be the most appealing at the time. It is defined as the combination of depth-first and breadth-first search algorithms. It uses both heuristics and search functions to perform its operations. We can use both methods while using the best-first search. At each stage, we may use the best-first search algorithm to select the most promising node from the graph. We expand the node that is closest to the goal node in the best-first search process, and the closest cost is determined using a heuristic function, i.e. For GreedyBFS the evaluation function f(n) is given as:

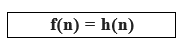
Where h(n) is the heuristic function which is defined as the distance of approximation of how close we are to the goal from a given node. The time complexity of the algorithm is given as O(n*logn).

5. A*(A-STAR) Algorithm: A star algorithm is one of the best and most popular pathfinding algorithms to this day. To identify the next node to be examined, the A* algorithm combines the actual cost from the starting point with an estimated price to the endpoint. The heuristic function used in A* calculates the estimated cost. A* algorithm always finds the best path to the destination node given a starting node in a network. The procedure entails creating all potential pathways from the initial node and examining nearby nodes one by one until reaching the node designated as the destination node. A* employs the "f" value, which is defined as:

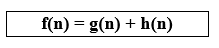
Where g(n) is the distance between the start node to some node n, h(n) is the estimated cost by heuristic function from node n to the goal node.

A. Heuristics

Heuristics, also known as heuristic functions, offers 'good enough' answers to complicated problems where finding the ideal solution would take too long. When you utilize heuristics, you give up precision, correctness, and exactness in exchange for speed. One of Dijkstra's algorithm's limitations is that it can (and will) consider pathways that will never offer the shortest path. Consider locating the quickest route between Delhi and Agra using a map. Anyone with a basic understanding of Indian geography would always choose the Yamuna Expressway as the route since it is the shortest route between the two cities. It's crucial to strike a balance between speed and accuracy. In certain cases, precision is less critical than the speed of processing. Heuristics can be calculated using the following methods:

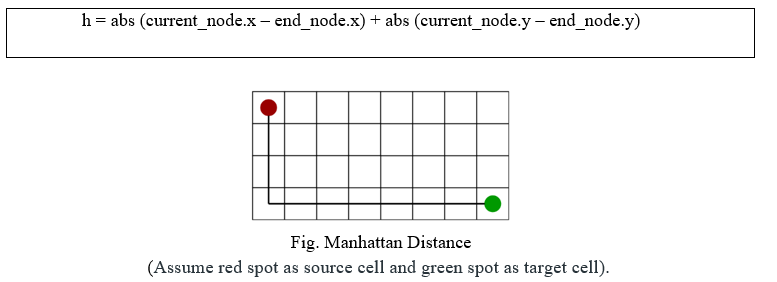
1. Manhattan Distance: The sum of absolute values of differences in the end node’s x and y coordinates and the current node’s x and y coordinates respectively. We use these heuristics when we are allowed to move only in four directions (right, left, up, down,).

2. Diagonal Distance: It is defined as the sum of the absolute values of the differences between the target's x and y coordinates and the present cell's x and y coordinates i.e.

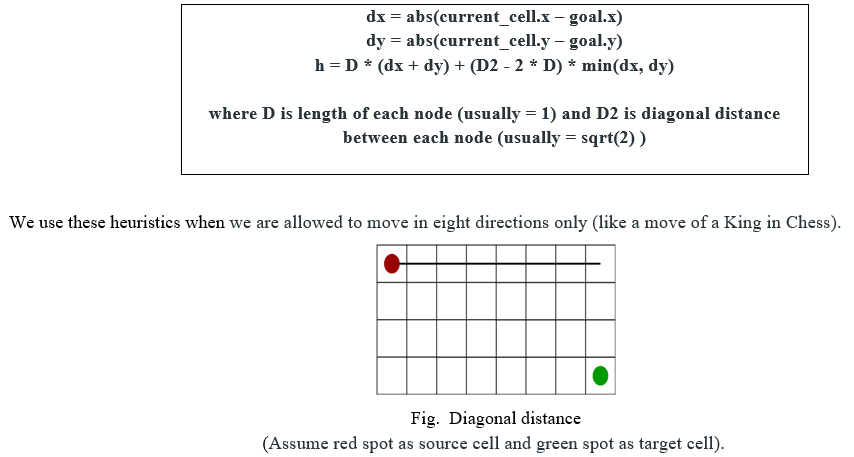
3. Euclidean Distance: It is defined as the distance between the current cell and the goal cell using the distance formula:

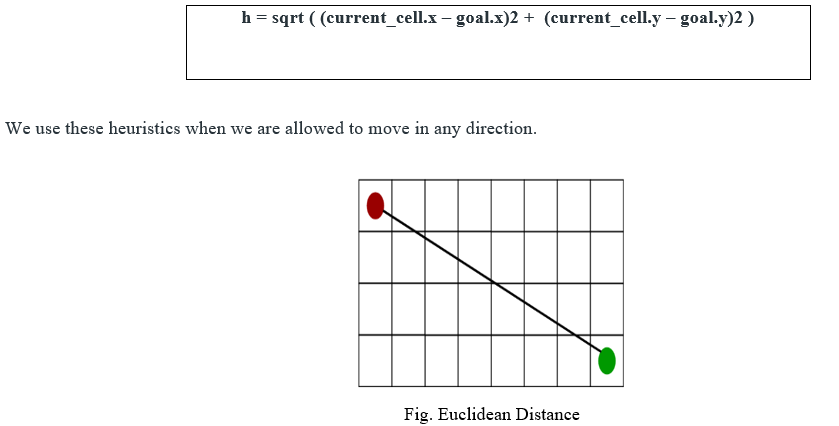
B. Pseudocode for A* algorithm:

WHY A* STAR ALGORITHM IS BETTER THAN DIJKSTRA

So, what is the point of the A*algorithm? Informally, unlike other traversal approaches, A* Search algorithms have "brains." What this means is that it is a smart algorithm, which distinguishes it from other traditional algorithms such as Dijkstra.

Dijkstra Algorithm - This algorithm operates by checking each closest point in all directions that have not yet been visited and expanding until it reaches the target. Because it verifies all of the nodes, this technique is guaranteed to discover the shortest path to the goal. However, because it examines all of the nodes, it will get much slower the longer it runs because it will be checking more and more nodes each time. The A* algorithm is a variant of the Dijkstra algorithm.

IV. IMPLEMENTATION

We will be implementing particularly A star pathfinding algorithm in Unity 3d, using C # as a programming language.

A. Creating 3d Environment

First, we will make a new 3d scene, in which there is a plane, obstacles (3d objects like a cube), starting point, and an endpoint.

B. Creating the Node Script and Grid Script.

We start off by designing the nodes for our 3d environment. That will help us apply the A* algorithm in the 3d Environment.

1. Defining a Node: First, we removed the mono behavior as we don’t need it. We'll now initialize two variables so that we can track the position in the array. We'll call this grid-X and grid-Y. We will also make a Boolean variable called bIsWallto tell whether or not the node is being obstructed or not. We will also use the Vector3 variable called position to track the nodes' real-world position. We will also create a node called parent; this is for the A star algorithm so that we can trace the path if it has been found back to the beginning. We will also need 3 integers g-cost, h-cost, and f-cost. We can make a get function to return the sum of them. Finally, we made a node function that takes arguments like a Boolean to set the wall variable, Vector3 to set the position, and two integers to set the grid position.

That concludes the node class.

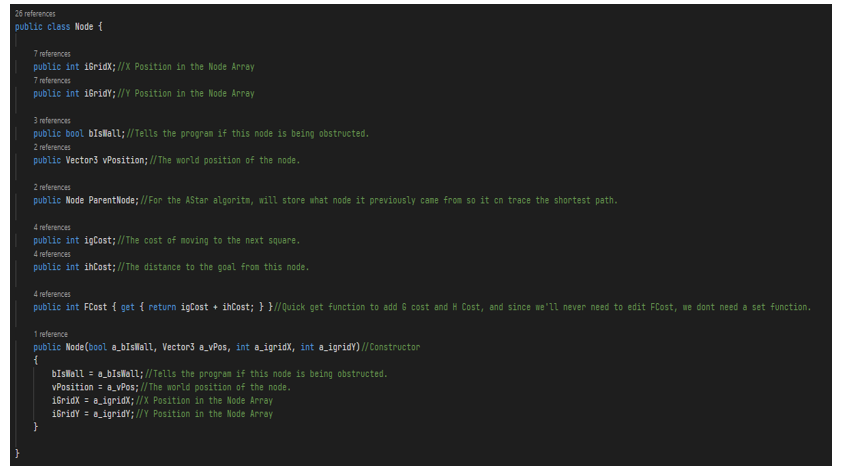
2. Script for Creating the Grid: First, we will be adding a function called the Start function, here we'll set the fNodeDiameter to be twice the fNodeRadius, then we'll divide the size of the GridWorldSize by the size of the fNodeDiameterin both axis, and then we will round it up to the nearest integer using Mathf.RoundToInt function.

Now we will proceed to create the grid function.

This CreateGrid function will be just a void and it doesn’t take any arguments. Now we'll create the NodeArraywhich declares the array of nodes. We need to get the real-world position of the bottom left of the grid, to do that we’ll use some vector math. This can be done as shown in the snippet. We'll then use a double for-loop to loop through the array of nodes one by one. To get the world coordinates of the bottom left of the graph we will use again some vectors shown below in the snippet. We'll initialize a Boolean variable wall and set it to True, we'll check if the node is not being obstructed and quick collision check against the current node and anything in the world at its position. We will also check if it is colliding with an object with a Wall Mask. if it, is we will set the bool to False. We'll then just create a new node in the array at that position using the variables we just calculated as the arguments.

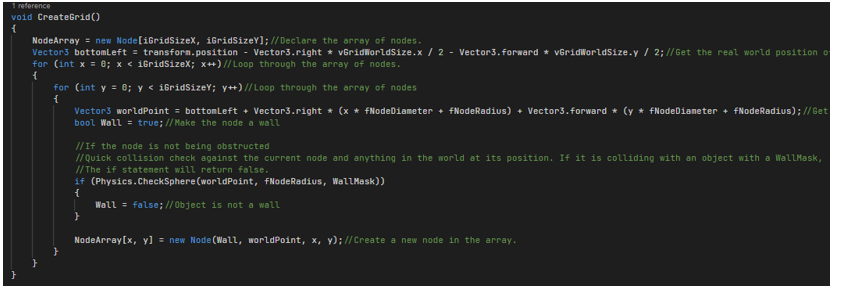
C. Script for drawing/showing gizmos in 3d environment

Now we will draw the grid using Unity's gizmos. We will create a function OnDrawGizmos which will contain all the logic for coloring the gizmos, Normal color of the wall is white, otherwise, it is yellow. We will also set the traced path color with red.

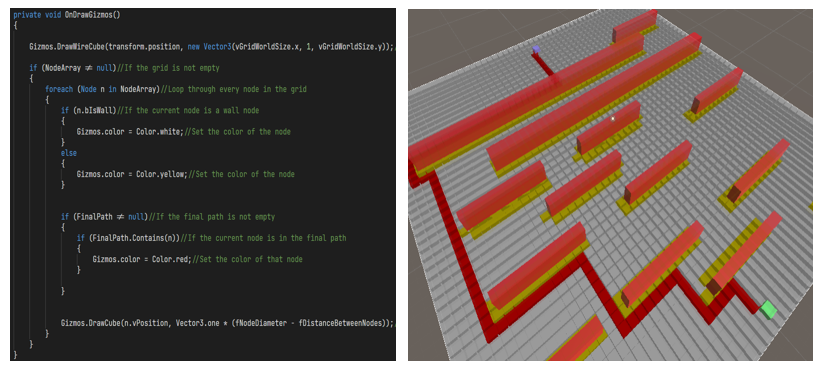
7. Script For Pathfinding Algorithm

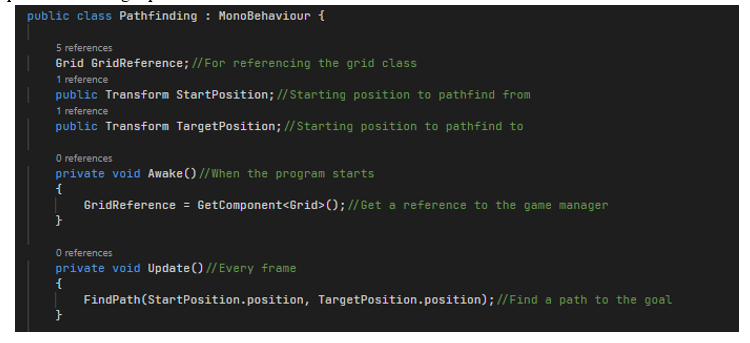
First, we'll initialize three variables, GridReference to reference the Grid class, and two public Transforms Start Position and the target position.

Next, we will update the awake function; this function will get called when the program will start. Here we will get the reference of the game manager object. Now we will edit the update method, this function will call every frame of the game. Here we will continuously find the path to the goal.

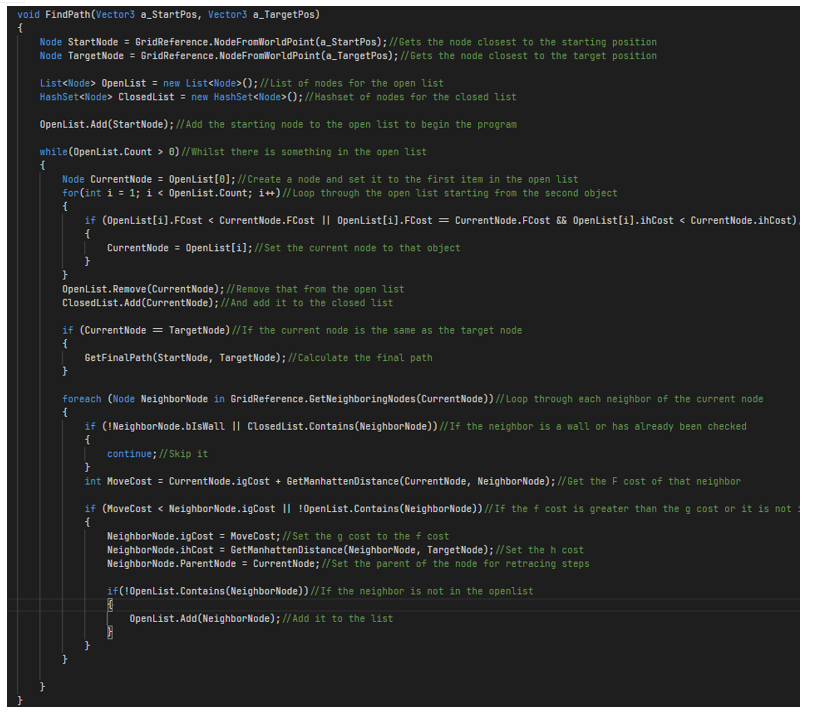
We will need a function that gets the closest node to the given world position, so we will create a function NodeFromWorldPoint in the grid script. It will take a vector3 argument WorldPos. Next, we will initialize two variables that convert world position to position in the node array. We will then clamp these variables between zero and one using Mathf.Clamp01 function. Next, we will calculate the correct position in the node array by multiplying the grid size by position variables and rounding it to an integer. Finally, we will return the node. Now we will define a FindPath function in the pathfinding script, It will take two vector3 arguments start position and target position.

We will declare two-node variables that get the node closest to the starting position and target position. Now we will declare a list called Open List which will store all the discovered nodes that are not evaluated yet. We will also declare a HashSetClosedList which we will use for the closed set as it will be perfect as it works the same as the list but does not hold any values for the variables.

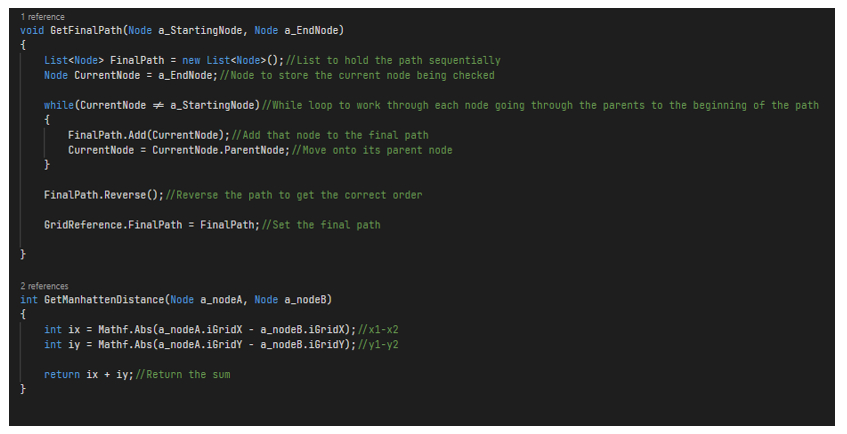
Next, we will add the starting node to the open list to begin the program. We will create a while loop that will active till there is something in the list. Then we will create a node and set it to the first item in the open list. We will now loop through the open list starting from the second object. Next, we will check if the f cost of that object is less than or equal to the f cost of the current node, if true we will set the current node to that object. Next, we will remove the current node from the OpenList and add it to the ClosedList.Next, we will check If the current node is the same as the target node, if it is true then we will calculate the final path by using a function called GetFinalPath which will take two arguments as StartNode and TargetNode. We will now define the GetFinalPath method in the pathfinding script. We will create a list to hold the path sequentially. Next, we will define a node variable to store the current node which is being checked.Now we will make a while loop to work through each node going through the parents to the beginning of the path. Then we will add that node to the final path using FinalPath.Add() method. Then we will move to its parent node.After while loop we will reverse the path to get the correct order and finally set the final path by GridReference. FinalPath.Next, we will create a method in grid script that gets the neighboring nodes of the given node. This method we call as GetNeighboringNodes. This method will return a list of nodes and take a single node as an argument. The whole code is defined below in a snippet. Now we will go back to our pathfinding script and update FinalPath method. We will loop through each neighbour of the current node and check if the neighbour is a wall or has already been checked. If true we will skip it and calculate the MoveCost which is F cost, by adding G cost and H cost. For H cost we will define a method called GetManhattenDistance later in the pathfinding script. Next, we will check if the f cost is greater than the g cost or it is not in the open list, if true we will set the g cost to the f cost. Then we will set the h cost and the parent node for the retracing steps. Again we will check If the neighbour is not in the OpenList, if true we will add it to the list by OpenList.Add() method.

Next, we will define the method GetManhattenDistance, it will take two nodes as an argument and return the sum of absolute differences of GridX and GridY from both the nodes.

V. FINAL IMPLEMENTATION

In unity, we will drag the pathfinding script onto the Gamemanager object.

Then when we click to play, the red path should appear between the Start and Target, we can find the shortest path from starting to the endpoint using A* algorithm.

Conclusion

We have successfully implemented the A star pathfinding algorithm in Unity 3d using C# as a programming language. We have learned about Unity Game Engine, Object-Oriented Programming, the Concept of baking in Unity 3d, and much other information on pathfinding algorithms. We have got a decent knowledge of the differences between different pathfinding algorithms. Terrain and large maps in Unity 3d take much more processing power to individually generate nodes for calculating the path between the start position and end position. We still have to work on optimizing the generation of nodes with different environments in Unity 3d.

References

[1] “AI and Navigation,” Epic Games Inc., Available: https://docs.unrealengine.com/udk/Three/AIAndNavigationHome.html. [2] “Using Games Engine to Implement Intelligent Virtual Environments” by Calderon, Carlos & Marc Cavazza, [3] “Understanding Dijkstra’s Algorithm” by Muhammad Adeel Javaid. [4] “A Comparative Study of A-star Algorithms for Search and rescue in Perfect” by Maze Xiang Liu and Daoxiong Gong [5] “Heuristic Pathfinding Algorithm Based on Dijkstra” by Yan-Jiang SUN, Xiang-Qian DING and Lei-Na JIANG. [6] Dijkstra’s Algorithm, Available at http://informatics.mccme.ru/moodle/mod/statements/ view.php?id=193#1. 2012. [7] “A Review And Evaluations Of Shortest Path Algorithms” by KairanbayMagzhan and Hajar Mat Jani. [8] “Dissecting Games Engines: the Case of Unity3D “ by Farouk Messaoudi, Gwendal Simon and AdlenKsentini. [9] “3D Game Development Using Unity Game Engine” by Pa.Megha, L.Nachammai and T.M.Senthil Ganesan.

Copyright

Copyright © 2022 Mohammad Aakil Iqbal, Hritik Panwar, Satya Prakash Singh. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.