Design and Performance Analysis of Short Time Fourier Transform Processor

Abstract

Time-frequency domain characterization of signals have always been focused on variants of Short time Fourier transform (STFT). The selection of transform kernel plays an important role in preserving the signal support which provides a cross-term free time-frequency distribution. Time-Bandwidth product has been taken as a measure of signal support preservation criteria thereby developing an optimal kernel for STFT based on linear canonical decomposition. In the development of kernel , Fractional Fourier Transform (FrFT) is used which provides noise free frequency domain representation .With the help of developed transform kernel , the magnitude-wise shift invariance property is verified and time-frequency content is analyzed by plotting spectrogram.

Introduction

I. INTRODUCTION

Frequency domain representation is an important tool to analyze some of the signals compared to time domain. Some of the mathematical computations like convolution can be easily converted into multiplications in frequency domain. Apart from analyzing the signals in frequency domain, investigating time and frequency content simultaneously is useful in finding the frequency details of a signal at different particular time instants.

For the analysis of time-frequency content, various transform techniques have been proposed out of which Short Time Fourier Transform (STFT) is an efficient technique. In STFT a kernel or a window of fixed size is selected and  it is applied all throughout the signal, resulting transform is obtained and time-frequency content is plotted by means of a spectrogram. This STFT technique efficiency is determined by various factors. Some of the factors include selection of kernel, choice of optimal fractional Fourier order and cross term free distribution. With the help of this STFT, applications like Chirplet modeling, Time scale modification, Frequency scaling, Fundamental frequency estimation from spectral peeks can be implemented with high accuracy.

This TBP optimal STFT has many advantages over conventional STFT. Some of the advantages include, it is more accurate than other transforms, it is computationally simple, by using it is possible to compare both time and frequency content and this STFT is cross term free.

An example of distribution which best suitable for STFT is Wigner distribution. But, Wigner distribution is affected by the inherent problem of cross terms which fails to preserve the signal support. Hence, the aim is to develop a kernel which is free of cross terms and preserves the signal support. The Hermite Gaussian kernel is chosen as an optimal kernel. This kernel along with preserving the signal support also satisfies both the magnitude wise shift-invariance and rotation property of STFT.

However, STFT with the Gaussian kernel still suffers from the problem of limited resolution. To overcome the inherent tradeoff between the time and the frequency localization of the STFT, several alternatives have been investigated in the literature. In [5], using two kernel functions of different supports, a wideband and a narrowband spectrogram are obtained. In order to preserve the localization characteristics of both, a combined spectrogram is formed by computing the geometric mean of the corresponding STFT magnitudes, whereas in [6], the STFT is evaluated by using a kernel function with an adaptive width in order to analyze the transient response of radar targets. In [16], a kernel matching algorithm is developed by locally adapting the Gaussian kernel functions to the analyzed signal. Although these investigations provide significant improvements in the time-frequency localization of signal components, in the presence of chirp-like signals, they still provide descriptions whose localization properties depends on the chirp rate of the components. Recently, [7] introduced an improved instantaneous frequency estimation technique using an adaptive STFT where the kernel functions are chosen from a set of functions through adaptation rules and computation of the STFT with varying kernel functions at each time instance. In addition, apart from the analysis of deterministic signals, there have been studies where time-varying spectra of random processes are investigated [17].

In this paper, we characterize the time-frequency domain localization by STFT and investigate the effect of the STFT kernel on the obtained time-frequency representation of signals. We introduce the time-bandwidth product (TBP) definition to provide a rotation-invariant measure of signal support in the time-frequency domain. Then, we obtain the optimal STFT kernel that provides the most compact representation considering the TBP of a signal component. The proposed time-frequency analysis is shown to be equivalent to an ordinary STFT analysis conducted in a scaled fractional Fourier transform domain. The obtained TBP optimal STFT representation yields optimally compact time-frequency supports for chirp-like signals on the STFT plane. In general, the TBP optimal STFT representation does n

II. LINERA SHIFT INVARIANT TIME FREQUENCY DISTRIBUTION

ot satisfy the rotation property. However, as shown in detail, there exists a linear canonical decomposition of the TBP optimal STFT that provides the link between the TBP optimal STFT and the rotation invariance property.

A. Road map of this paper

This paper is organized as follows. In Section II, we show that the STFT is the only linear time-frequency representation that satisfies the magnitude-wise shift invariance property. In Section III, we provide the linear canonical decomposition of STFT by developing an optimal STFT kernel. In Section IV, we introduce the Fractional Fourier transform algorithm and it’s application to provide a noise free frequency representation. In Section V, we plot the spectrogram for time-frequency analysis and SNR comparison for FrFT and FFT representations.

III. STFT BLOCK DIAGRAM

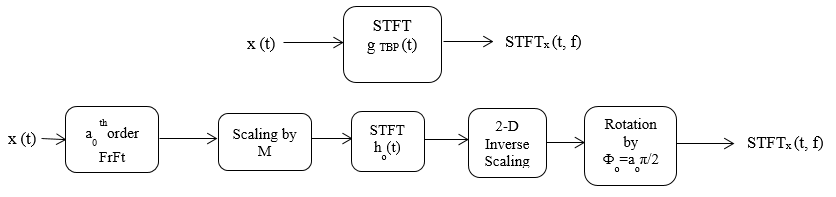
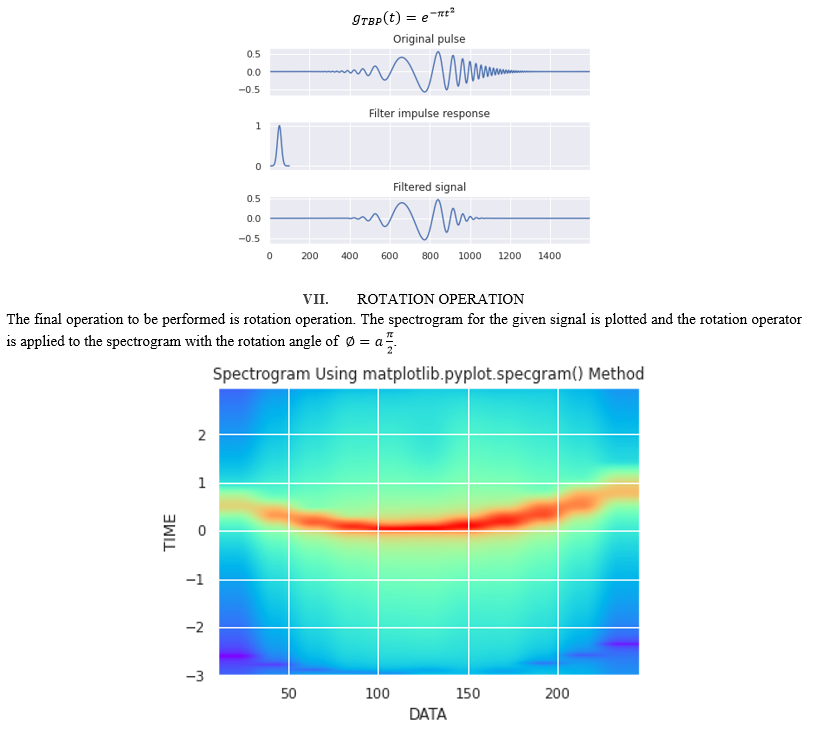
The development of STFT kernel can be achieved by the linear canonical decomposition of TBP optimal STFT analysis with a sequence of operations explained and illustrated as shown in the Fig.

First for the given input signal, a0 th order Fractional Fourier transform is calculated of different orders. From the obtained transforms optimal order is chosen from the spectral peaks of all order transforms. After time scaling operation is performed and then STFT is calculated by using Hermite Gaussian kernel. Then, time-frequency domain inverse scaling is performed and finally rotation is applied to the spectrogram with a rotation angle of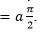

The main reason behind the introduction of this canonical decomposition is that the rotation invariant STFT with the zeroth-order Hermite-Gaussian kernel is explicitly shown to be part of every TBP optimal STFT analysis. Therefore, for any arbitrary mono-component signal, there exists a “natural domain,” where the rotation independent STFT analysis with zeroth-order Hermite–Gaussian kernel provides the TBP optimal STFT representation. The signals are transformed to their “natural domains” by the first two operations of the canonical decomposition. We believe this concept of “natural domain” is theoretically significant and will provide further insight to the research on time-frequency signal analysis. In the rest of this section, the performance of the TBP optimal STFT is illustrated by using simulated data. In the simulations, we use a quadratic FM signal embedded in -5 dB noise. The analyzed signal is

A significant improvement for the time-frequency localization is observed when compared with the TBP optimal STFT with similar computational complexity. As future work, optimal STFT analysis will be extended to multicomponent signals. To obtain a well-localized time-frequency representation of a multicomponent chirp signal with different chirp rates, the orientation angles of each component and, consequently, the required FrFT orders to perform the STFT, should be determined. Following the individual GTBP optimal time-frequency analysis of each signal component, the obtained time-frequency representations are combined so that the time-frequency localization of each chirp component is optimally compact.

IV. FrFT ALGORITHM

Fractional Fourier Transform is a generalized Fourier transform calculated for different fractional Fourier orders which transforms the signal from time domain to frequency domain. The first order fractional Fourier transform is called Fourier transform. In the analysis for development of STFT kernel, FrFT is the first step. The FrFT algorithm includes the following steps.

1. Chirp multiplication.
2. Chirp convolution.
3. Chirp multiplication.

Before applying above operation on input signal, modulo operation is performed to limit the range of fractional Fourier order a between 0.5 and 1.5. FrFT of input signal is calculated for different fractional Fourier orders. Then optimal order is selected from the spectral peaks of various orders. The given FrFT algorithm has a complexity of O(NlogN) and the complexity reduces compared to the conventional FrFT algorithm with complexity O(N2).

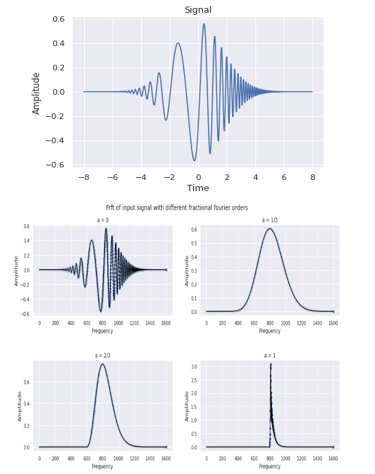
In the simulation we use a linear frequency modulated signal as given by the equation written in section ?. After finding the Fractional Fourier transform for different twenty to thirty fractional Fourier orders, an optimal Fractional Fourier order is selected from the spectral peaks of the obtained plots. The optimal Fractional Fourier order lies in the range of 0.5 to 1.5. The limiting of Fractional Fourier order between this range is done by using modulo operation to ensure the optimal rotation angle used in the rotation  operator for the rotation of the spectrogram.

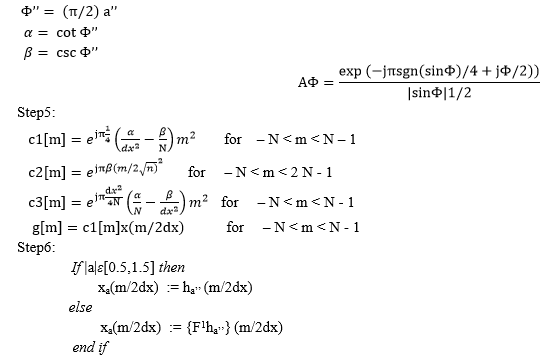
V. TIME SCALING

For the development of STFT kernel the next operation to be performed is time scaling. The input signal is downscaled by a factor α  and then the fractional Fourier transform is applied on the scaled signal with the obtained optimal Fractional Fourier order. Here we downscaled the input signal by 100 times and the resultant Fractional Fourier transform plots obtained are as shown below,

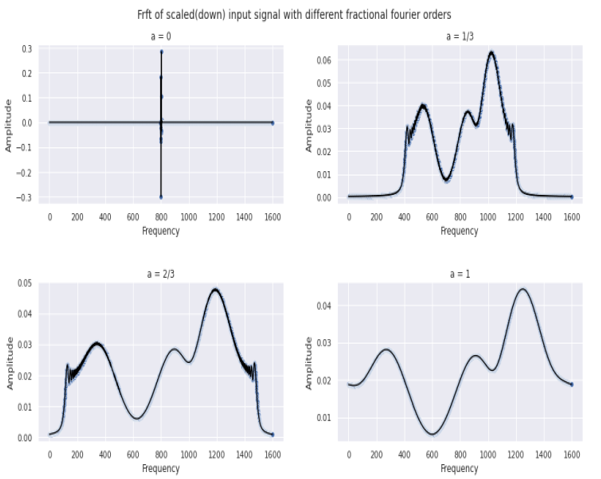
VI. APPLICATION OF OPTIMAL STFT KERNEL

After time scaling and transforming the scaled signal using FrFT, the output signal is multiplied with Hermite Gaussian kernel of the form as given below,

VIII. APPLICATION OF FRFT IN NOISE REDUCTION

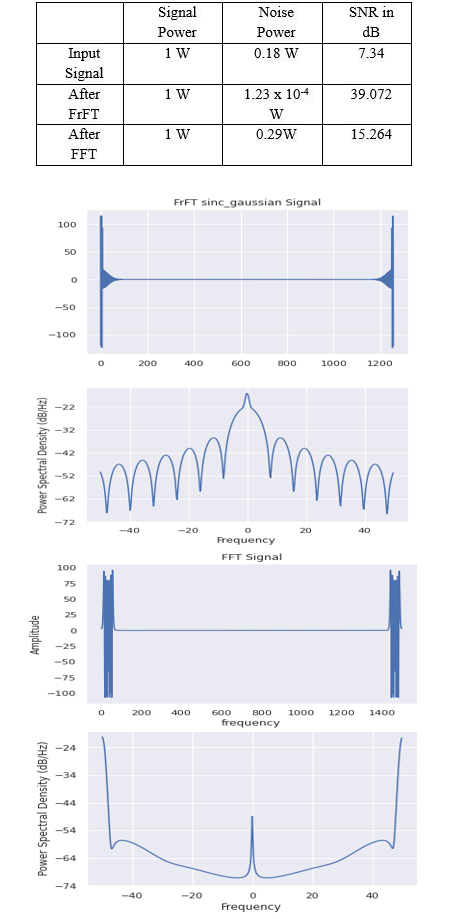
Fractional Fourier transform is used to eliminate noise in signals. Hence it finds it’s applications in SONAR signal processing and finding targets using RADAR. Here we compare the performance of FrFT with FFT in the presence of noise. For comparison of FrFT and FFT, we choose Signal to Noise Ratio(SNR) as a comparison parameter. The power of input signal and noise signal is found by using the area of their respective Power Spectral Density (PSD) curves. Then the input signal corrupted with noise is transformed into frequency domain using both FrFT and FFT. After inverse transformation, the power of input is again calculated by using PSD curves and SNR is calculated in both cases. It is observed that SNR in case of FrFT is more as compared to FFT. Hence FrFT can be used in noise reduction of signals.

In this paper, we developed the STFT equation with the help of linearly decomposed kernel. Further the architecture of above STFT block diagram can be mapped and it can be implemented using an FPGA. Then, the STFT processor is said to be implemented and its hardware complexity can be measured.

X. APPENDIX

References

[1] F. Hlawatsch and G. F. Boudreaux-Bartels, “Linear and quadratic timefrequency signal representations,” IEEE Signal Processing Mag., vol. 9, pp. 21–67, Apr. 1992. [2] L. Cohen, “Time-frequency distributions—A review,” Proc. IEEE, vol. 77, pp. 941–981, July 1989. [3] Time-Frequency Analysis. Englewood Cliffs, NJ: Prentice-Hall, 1995. [4] R. A. Altes, “Detection, estimation and classification with spectrograms,” J. Acoust. Soc. Amer., vol. 67, no. 4, pp. 1232–1246, Apr. 1980. [5] S. Cheung and J. S. Lim, “Combined multiresolution (wideband/narrow-band) spectrogram,” IEEE Trans. Signal Processing, vol. 40, pp. 975–977, Apr. 1992. [6] E. J. Rothwell, K. M. Chen, and D. P. Nyquist, “An adaptive-windowwidth short-time Fourier transform for visualization of radar target substructure resonances,” IEEE Trans. Antennas Propagat., vol. 46, pp. 1393–1395, Sept. 1998. [7] H. K. Kwok and D. L. Jones, “Improved instantaneous frequency estimation using an adaptive short-time Fourier transform,” IEEE Trans. Signal Processing, vol. 48, pp. 2964–2972, Oct. 2000. [8] LJ. Stankovic, “A method for time-frequency signal analysis,” IEEE Trans. Signal Processing, vol. 42, pp. 225–229, Jan. 1994. [9] P. K. Kumar and K. M. M. Prabhu, “Simulation studies of moving-target detection: A new approach with Wigner-Ville distribution,” Proc. Inst. Elect. Eng. Radar. Sonar Navig., vol. 144, pp. 259–265, Oct. 1997. [10] P. Flandrin, “Some features of time-frequency representations of multicomponent signals,” in Proc. IEEE Int. Conf. Acoust. Speech Signal Process., vol. 9, 1984, pp. 266–269. [11] K. J. R. Liu, “Novel parallel architecture for short-time Fourier transform,” IEEE Trans. Circuits Syst., vol. 40, pp. 786–789, Dec. 1993. [12] M. G. Amin and K. D. Feng, “Short-time Fourier transform using cascade filter structures,” IEEE Trans. Circuits Syst., vol. 42, pp. 631–641, Oct. 1995. [13] W. Chen, N. Kehtarnavaz, and T. W. Spencer, “An efficient recursive algorithm for time-varying Fourier transform,” IEEE Trans. Signal Processing, vol. 41, pp. 2488–2490, July 1993. [14] A. W. Lohmann and B. H. Soffer, “Relationships between the RadonWigner and fractional Fourier transforms,” J. Opt. Soc. Amer. A, vol. 11, pp. 1798–1801, 1994. [15] J. C. Wood and D. T. Barry, “Radon transformation of time-frequency distributions for analysis of multicomponent signals,” IEEE Trans. Signal Processing, vol. 42, pp. 3166–3177, Nov. 1994. [16] G. Jones and B. Boashash, “Generalized instantaneous parameters and window matching in the time-frequency plane,” IEEE Trans. Signal Processing, vol. 45, pp. 1264–1275, May 1997. [17] L. L. Scharf and B. Friedlander, “Toeplitz and Hankel kernels for estimating time-varying spectra of discrete-time random processes,” IEEE Trans. Signal Processing, vol. 49, pp. 179–189, Jan. 2001. [18] A. W. Naylor and G. R. Sell, Linear Operator Theory in Engineering and Science. New York: Springer-Verlag, 1982. [19] L. B. Almedia, “The fractional Fourier transform and time-frequency representations,” IEEE Trans. Signal Processing, vol. 42, pp. 3084–3091, Nov. 1994. [20] V. Namias, “The fractional order Fourier transform and its application to quantum mechanics,” J. Inst. Math. Appl., vol. 25, pp. 241–265, 1980. [21] H. M. Ozaktas, Z. Zalevsky, and M. A. Kutay, The Fractional Fourier Transform With Applications in Optics and Signal Processing. New York: Wiley, 2000. [22] H. M. Ozaktas, N. Erkaya, and M. A. Kutay, “Effect of fractional Fourier transformation on time-frequency distributions belonging to Cohen class,” IEEE Signal Processing Lett., vol. 3, pp. 40–41, Feb. 1996. [23] H. M. Ozaktas, O. Ar?kan, M. A. Kutay, and G. Bozdagi, “Digital computation of the fractional Fourier transform,” IEEE Trans. Signal Processing, vol. 44, pp. 2141–2150, Sept. 1996. [24] J. C. Wood and D. T. Barry, “Tomographic time-frequency analysis and its application toward time-varying filtering and adaptive kernel desing for multicomponent linear-FM signals,” IEEE Trans. Signal Processing, vol. 42, pp. 2094–2104, Aug. 1994. [25] “Linear signal synthesis using the Radon-Wigner transform,” IEEE Trans. Signal Processing, vol. 42, pp. 2105–2111, Aug. 1994. [26] Z. Bao, G. Wang, and L. Luo, “Inverse synthetic aperture radar imaging of maneuvering targets,” Opt. Eng., vol. 37, no. 5, pp. 1582–1588, May 1998. [27] A. K. Özdemir and O. Ar?kan, “Efficient computation of the ambiguity function and the Wigner distribution on arbitrary line segments,” IEEE Trans. Signal Processing, vol. 49, pp. 381–393, Feb. 2001. [28] H. Ozaktas and O. Aytür, “Fractional Fourier domains,” Signal Process., vol. 46, pp. 119–124, 1995. [29] S. Shinde and V. M. Gadre, “An uncertainty principle for real signals in the fractional Fourier transform domain,” IEEE Trans. Signal Processing, vol. 49, pp. 2545–2548, Nov. 2001. [30] A. Bultan, “A Four-Parameter Atomic Decomposition and the Related Time-Frequency Distribution,” Ph.D. dissertation, Dept. Electr. Electron. Eng., Middle East Tech. Univ., Ankara, Turkey, 1995. [31] , “A four-parameter atomic decomposition of chirplets,” IEEE Trans. Signal Processing, vol. 47, pp. 731–745, Mar. 1999. [32] S. Pei and M. Yeh, “A novel method for discrete fractional Fourier transform computation,” in Proc. IEEE Int. Symp. Circuits Syst., vol. 2, 2001, pp. 585–588. [33] O. Akay and G. F. Boudreaux-Bartels, “Fractional autocorrelation and its application to detection and estimation of linear fm signals,” in Proc. IEEE-SP Int. Symp. Time-Freq. Time-Scale Anal., 1998, pp. 213–216. [34] T. Alieva and M. J. Bastiaans, “On fractional Fourier transform moments,” IEEE Signal Processing Lett., vol. 7, pp. 320–323, Nov. 2000. [35] L. Stankovic, T. Alieva, and M. Bastiaans, “Wigner distribution weighted in the fractional Fourier domains,” in Proc. ProRISC, Veldhoven, The Netherlands, Nov. 2001, pp. 635–640. [36] F. Zhang, Y. Q. Chen, and G. Bi, “Adaptive harmonic fractional Fourier transform,” IEEE Signal Processing Lett., vol. 6, pp. 281–283, Nov. 1999. [37] A. K. Özdemir, L. Durak, and O. Ar?kan, “High resolution time-frequency analysis by fractional domain warping,” in Proc. IEEE Int. Conf. Acoust., Speech, Signal Process., May 2001. [38] A. J. E. M. Janssen, “On the locus and spread of pseudo-density functions in the time-frequency plane,” Philips

Copyright

Copyright © 2022 Manikanta Neralla, Venkata Reddy Jillela, Chakri Lolugu, Sravan Kumar Paidi, Janaki Ram Kilari, Dr. M. V. Nageswara Rao. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.