Effect of Mono-Dispersed Solids Slurry Characteristics on Horizontal Bends

Abstract

Erosion in multiphase flow due to the effect of solid particles is a key factor in wearing of industrial pipelines. In recent years, industries are using Computational Fluid Dynamics to study erosion wear in pipelines. Researchers have investigated various factors that affect the erosion of pipelines including particle size, velocity, coating material, fluid viscosity, region of pipe (bends/fittings convex or concave), etc. This paper investigates the effect of various slurry parameters on the rate of material erosion in the pipeline, under different sets of operation conditions. Silica sand (density= 2650 kg/m3) slurry was considered for the simulations, mixed in water at different volumetric concentration (12%, 24% and 36%), with an inlet velocity of 2.74 m/s and 3.56 m/s. The particle size was considered constant at 225µm, 450µm and 675µm, respectively. Simulations are done in ANSYS-FLUENT software under Eulerian two-phase model with k-? approach. Results showed that the erosion rate followed the trend of increasing with an increase in all the above mentioned varying parameters as it varied from 8.25 mm/yr to 18.93 mm/yr. It was also hinted that as particle size reduced, the influence of velocity as a contributing parameter reduced which is explained by the fact that the mixture is leading from suspension state to colloidal state.

Introduction

I. INTRODUCTION

Flows involving a suspension of fine solid materials in a flowing fluid have now been comprehensively used by various civilizations throughout history, more particularly by the Egyptian, Roman, and Greek empires. But the earliest evidence of solid-liquid suspension ?ows in an engineering application was from the 1860s in Egypt's Suez Canal [1].

Nowadays, pipelines are used to transport solids suspended in liquids in industrial fields such as chemical, food, and pharmaceutical production, mineral and construction material transportation (such as coal, iron ore, sand, crushed rock, cement, wet concrete, etc.), municipal and industrial wastes, and emerging industries related to "smart" materials and biological systems. Hundreds of additional products in diverse areas, such as radioactive materials, grains, and hospital supplies, also use this mode of transportation [2, 3, 4].

Understanding the characteristics of liquid & solid particles transport in industrial contexts requires instrumentation that can make fast, accurate, and autonomous measurements. These instruments are expected to be reliable, fast, and unobtrusive, i.e., they should not interfere with the monitored flow and require little maintenance.  Apart from monitoring, the information obtained through real-time observation allows technical experts to make more informed decisions based on solids behaviour, such as particle settling (that leads to pipe wear), clustering, or blockages that can potentially harm the device or cause breakdowns, both of which are costly [5].

In pipes that move bulk solids using both hydraulic and pneumatic conveying modes, erosion is an inevitable event. A number of factors, including material hardness, solid particle size and shape, concentration, particle velocity, solid impact angle on the target material surface, and others, affect erosion wear.

To establish the functional dependence of erosion wear on various parameters, several researchers have conducted systematic studies. Bahadur and Badruddin [6], Gandhi et al. [7], Singh et al. [8] investigated on how characteristics such as solid concentration, flow velocity and particle size in coal-water slurry influenced the erosion wear.

The impact of particle size, shape, and rotation on erosion was investigated by Deng et al. [9] and Heilbronner et al. [10]. They came to the conclusion that spherical particles had less of an impact on erosion than irregular particles did. Though the number of affecting factors are numerous with each having an independent influence on erosion, Gupta et al. [11] managed to create a relationship, an empirical formula, which has been preferred by many academics to estimate erosion rates. The equation is as expressed below:

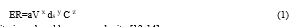
And in case of translatory motion, rotational velocity is replaced by mean velocity [12-14].

Other elements that influence erosion-corrosion in slurry pipelines but are left out of the equation above for the sake of computational ease include pH, the impact of using additive layers on the inner walls of pipelines, pipeline shape, etc. The effects of pH value on erosion in stainless steel pipes were examined by Hessari and Round [15], Singh et al. [16], and Kaushal et al. [17].

Any pipeline network must include bends, elbows, expansion-contraction joints, and other features that allow for flexible routing. However, few investigations on bends for solid-liquid two-phase flow have been conducted. Some of the prominent results in this domain are listed below.

According to numerous studies, a pipe bend ratio of 5 to 5.7 is ideal for minimising pressure drop around the curve [18, 23–24].

Kaushal et al. [24] studied the effect of pipe bends on pressure drop and concentration distribution, both experimentally and computationally, by using silica sand slurry and found that the optimum bend ratio for minimal pressure loss was 5.6.

In this paper, keeping the pipe bend ratio at an optimum ratio of 5.6, the effect of silica sand slurry characteristics have been observed on the erosion rate in a 90° horizontal pipe bend of aluminium with no coating. The volumetric concentration of the silica sand varies from 12% to 36% and for each concentration in this study. Two flow velocities and three constant particle sizes were considered, varying from 2.74 m/s to 3.56m/s and 225 µm to 675 µm respectively.

II. MATHEMATICAL MODELLING

A. CFD Modelling

Computational Fluid Dynamics is used to model the fluid (CFD). For all fluid simulations in this paper, the ANSYS FLUENT R19.0 Academic Package was used. FLUENT uses a finite volume approach in its CFD code. This is a common method that can be found in many CFD codes. The control volume is a defined zone in which the governing equations are applied. These equations are referred to as conservation equations because they describe the conservation of mass, momentum, and energy over the control volume.

In most cases, the simulation's multiphase model selection is based on the concentration of solid particles. It is critical to select the most appropriate model for one's needs because it distinguishes momentum transference. Given that slurries are not dilute fluids, the mixture and Eulerian models are the best fit for the research. Non-granular models, according to the Eulerian model, tend to exclude friction and inter-particle collisions. As a result, the granular Eulerian model appeared to be the best option in this case.

C. Turbulence Modeling

The k-ε model was first put forth by Spalding and Launder in 1972 [33]. Following this, the model has undergone further improvement and modification. By using the renormalization group (RNG) theory, Yakhot and Orszag [34] suggested improving the k-ε model. The RNG theory is used to empirically infer the constants of the conventional k-ε model. In order to produce better and more accurate predictions for changes in flow, such as flow separation and flow via curved geometries, this ensures that the k- ε model does not need to be adjusted repeatedly based on the type of flow. This results in a 10-15% reduction in computing effort [40].

D. Wall Effects

Due to the considerable gradient of the quantities close to the wall, fine grids are required. Due to the computation taking longer, requiring more memory and faster computer processing, as well as making the equations more complex, this raises the cost of the calculation. A wall function, which is a group of semi-empirical formulae and functions, enables a less expensive calculation by substituting the fine grids with a set of equations that relate the calculated variables at near-wall cells with the equivalent amounts on the wall. The wall function helps in the more accurate estimate of near-wall shear stresses for both liquid and solid phases. The rigorous and wall function approaches were both incorporated in the hybrid near-wall modelling that was included in the FLUENT. Areas of interest were identified from the rest of the pipe by using the former method on cases of fine mesh, while the latter was used on the remaining portion of the pipe. With regard to near wall effects, this technique provides an insight and a balance between computational efforts and modelling inaccuracies.

III. NUMERICAL SOLUTION

A. Geometry Modeling

As previously noted, a bend ratio with the least amount of pressure loss associated was chosen to describe the bend in light of the findings of several researchers. To evaluate the impact of erosion, a pipe with an internal diameter of 53.0 mm and a bend curvature radius of 148.4 mm was employed, yielding a bend ratio of 5.60.

Numerous researchers have demonstrated that changes in various parameters, such as efflux concentration, had little to no impact on the critical deposition velocity when it came to the inflow velocity [41–42]. Experimental research by Kaushal et al. [24] revealed that the threshold deposition velocity for this particular configuration was between 1.50 and 1.55 m/s. Since particle diameter is also one of the characteristics varied in this setup to observe its effect and the effect of particle diameter on critical velocity is not known by formulation, the initial inlet velocity condition were determined at a significantly higher value of 2.74 m/s and 3.56 m/s while keeping the same in mind.

It has been determined that establishing well-developed turbulent flow in a pipe requires a minimum of 30–50 times the bend diameter. A 6.5 m straight upstream pipe was selected with this in mind. To ensure appropriate monitoring of flow characteristics and re-distribution of solids in the downstream length, at least a length of 140D i.e. 10 m was employed as the downstream length.

Since it is a horizontal bend, the pipe was laid in the XY plane and the origin point was the centre of the velocity inlet face. The initial velocity was directed in the positive-Y direction and the outlet of the bend was towards the negative-X direction. The Z plane was intersecting the pipe at mid plane. 

GAMBIT software was used to generate the computational grid. It consisted of 3,890,258 cells and 4,503,654 nodes. The grid-independence tests were carried out ensuring that all other contributing parameters were constant for all the cases. The initial grid was refined by approximately quadrupling the number of cells from 894,774 cells to 3,890,258 cells and then doubling the same from 3,890,258 cells to 5,526,047 cells. There were no additional enhancements in the results in later case. Hence, the mesh consisting of 3,890,258 cells was considered optimum and suitable for simulation (Fig. 1).

B. Boundary Conditions

The velocity inlet, the wall boundary, and the pressure outlet are the three constraints of the calculation domain. At the inlet of the bend, fully developed velocity and profile of volume fraction across the cross-section both solid and liquid phases were provided. At the outlet of the 10 m long horizontal straight pipe, fully developed velocity and profile of volume fraction across the cross-section are generated.

C. Solution Convergence

The momentum equation was discretized using a second order upwind method, whereas the volume fraction, turbulent kinetic energy, and turbulent energy dissipation were discretized using a first order upwind method. These algorithms provided acceptable accurate solutions and convergence. Based on the residual value of the estimated variables, including mass, velocity components, turbulent kinetic energy, turbulent energy dissipation rate, and volume fraction, the convergence criterion is determined. The value for convergence in the current computation was set to one thousandth of the initial residual values.

IV. MODELLING RESULTS

A. Effect Of Slurry Characteristics On Erosion Rate

Owing to the necessary interest of flow characteristics and expected aggravated material loss around the pipe bends, the erosion rates are magnified and presented in Fig. 2-19. Each figure has the discrete phase concentration distribution on the left side which acts as the proof and the reason for generic erosion rate graph of the slurry represented on the right side, with respective legends. The material loss is represented in CGS units is modified into units accepted by industries and suitable to read using Eq. (xx).

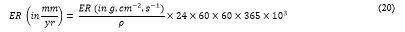
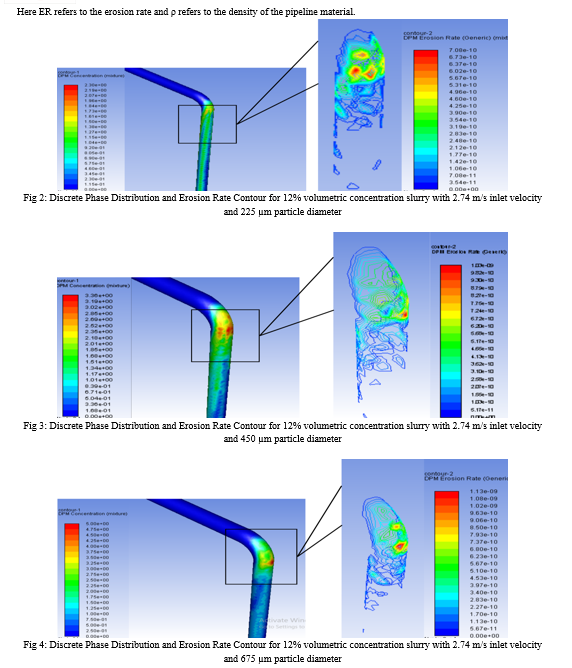
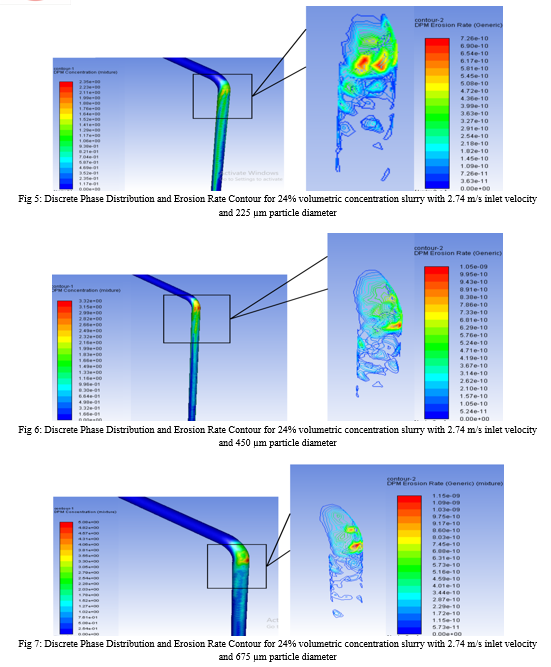
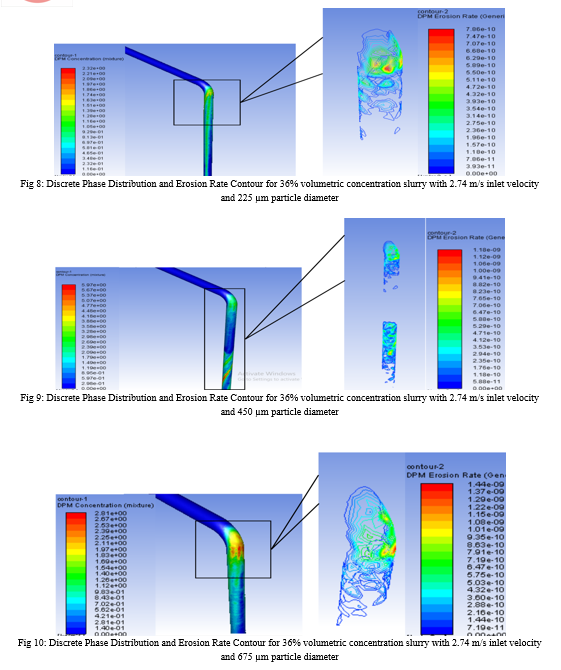
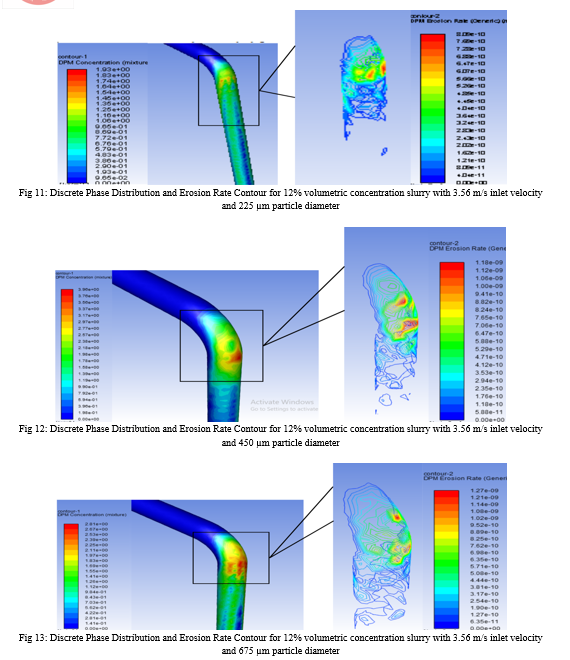
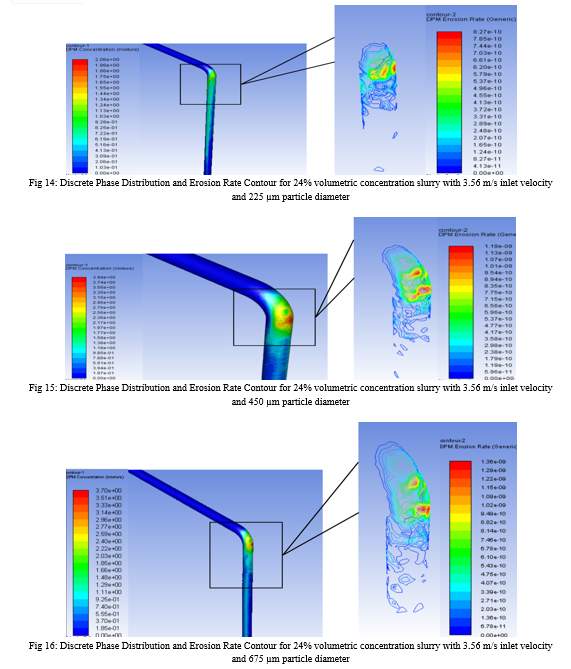
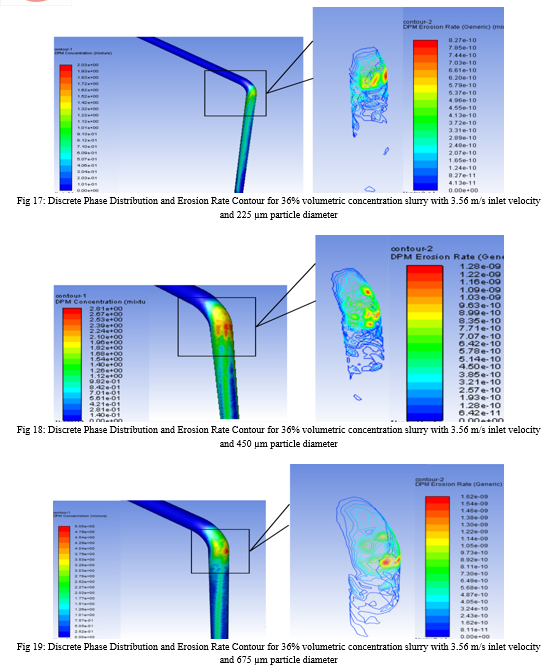
B. Effect Of Slurry Concentration On Erosion Rate

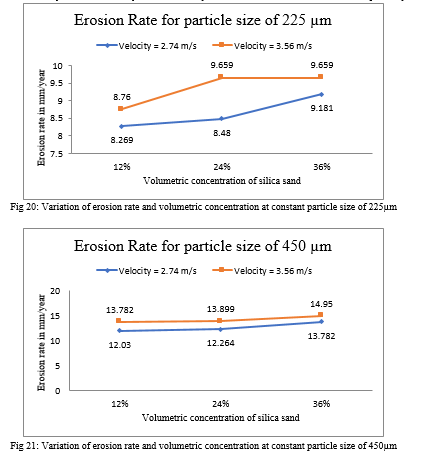
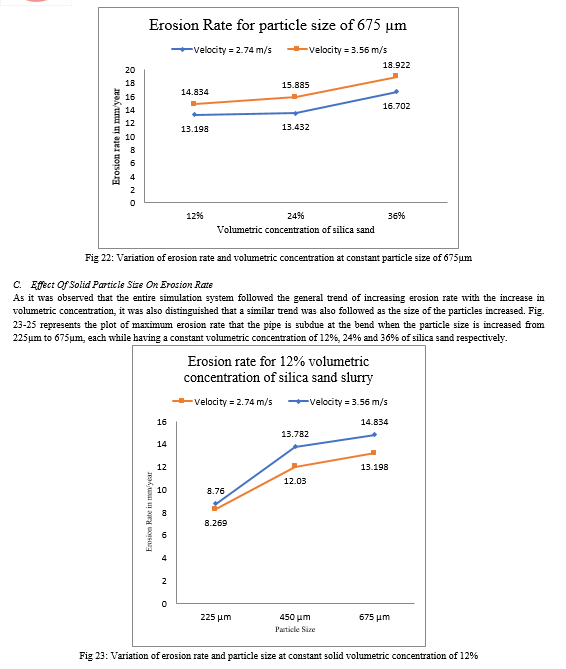
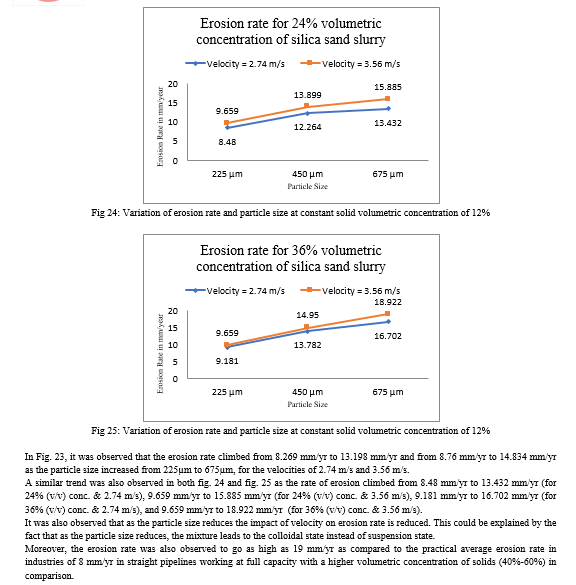
The variation of the slurry concentration flowing through the pipeline was done by keeping the cross-sectional area, particle size, inlet velocity and total mass flow rate constant. The inner diameter and radius of curvature of the bend of the aluminium pipe were maintained at 53 mm and 148.4 mm, respectively. The slurry concentration varied as 12%, 24% and 36% respectively and the maximum rate of erosion was recorded for each of the cases. Fig. 20-22 represents the plot of maximum erosion rate that the pipe is subdue at the bend when the volumetric concentration of silica sand increased from 12% to 36%, each while having a constant particle size of 225µm, 450µm and 675µm respectively.

In Fig. 20, it was observed that the erosion rate climbed from 8.269 mm/yr to 9.181 mm/yr as the volumetric concentration increased for the velocity of 2.74 m/s. However, for the velocity of 3.56 m/s, the erosion rate for both 24% and 36% volumetric concentration remained the same at 9.659 mm/yr while that for 12% volumetric concentration was observed to be 8.76 mm/yr.

Similarly, based on the boundary conditions given, it was observed in fig. 21 that the erosion rate increased from 12.03 mm/yr at 12% volumetric concentration of silica sand to 13.782 mm/yr at 36% volumetric concentration for the inlet velocity of 2.74 m/s. A similar trend was also observed when the inlet velocity was increased to 3.56 m/s as the erosion rate increased from 13.782 mm/yr at 12% (v/v) conc. to 14.95 mm/yr at 36% (v/v) conc.

The trends were observed to be similar again for increased particles size at 675µm in fig. 22 as the erosion rates increased from 13.198 mm/yr to 16.702 mm/yr and 14.834 mm/yr to 18.922 mm/yr for velocities 2.74 m/s and 3.56 m/s respectively.

Conclusion

The first-ever recorded experimentation published related to the solid-water mixture flow being in 1906 by Nora Blatch [1, 3], the field of slurry transportation can be considered as comparatively new and hence less investigated upon. However, given the numerous advantages, saved capital and environmentally friendly process it is, the interest in the field is not falsely hyped. Since the process is complex, numerous models and mathematical relations have been proposed related to different flow parameters. Rigidity in pipeline routing being one of the disadvantages has caught attention of researchers to investigate upon. In this paper, we investigated the slurry characteristics that affect the erosion rate under different sets of operating conditions. The inferences drawn from the results include: The overall erosion rate was found to be between 8.25 mm/yr to 18.93 mm/yr. This value is comparatively higher to the average practical erosion rate in industries i.e. 8-10 mm/yr, even though they operate at higher solid concentration. However, this concern can be tackled with future researches on alternate pipeline-slurry combinations, suitable pipeline coating which has been proven to significantly reduce the erosion rate and optimum bend angles for reduction of erosion rate. The discrete phase distribution around the pipe bends was inclined towards the outer surface of the pipeline, which can be explained by presumable vortex formation during the flow. Owing to the peculiar distribution of discrete phase around pipe bends, the outer walls of the bends are expected to be at a greater risk for aggravated material loss. This can be inferred from the fact that the erosion rates in the results were as high as 18.93 mm/yr which is 89% more than the average erosion rate faced in practical industrial pipelines. Under the limited set of sample points, it was observed that the rate of erosion was increasing with increase in velocity, particle size and volumetric concentration, which seconds the findings of different researchers. As the particle size decreased, velocity was observed to be a less significant parameter for the rate of erosion as the mixture led to colloidal state from suspension state. This is observed when a 30% increase in velocity showed a mere 5.2% and 5.9% increase in erosion rate for 24% and 36% volumetric concentration of solids Nomenclature Symbol Nomenclature ER Erosion/Wear rate V Speed of rotation C Slurry concentration (% by weight) a,x,y,z Constants depending on the process of erosion and material properties ?s, ?f Volumetric concentrations of solid and fluid phase, respectively ?P Static pressure gradient ??P?_s Inertial forces Ksl, Kls Interphase momentum exchange coefficient Cvm Coefficient of virtual mass force CL Lift coefficient (v_s ) ?,(v_l ) ? Velocities of solid and liquid phases, respectively (?_s ) ?,(?_l ) ? Viscous stress tensors for solid and liquid phases, respectively (?_(f,l) ) ? Reynolds stress tensor ? Mass density g ? Acceleration due to gravity I ? Identity tensor ?_s Bulk viscosity of solid ds Diameter of particles Go,ss Radial distribution function ?s,max Static settled concentration ?_s Granular temperature ?_s,?_l, µ Shear viscosity for solid, liquid phases and slurry, respectively ?_(s,col),?_(s,kin),?_(s,fr) Collisional, Kinetic and Frictional viscosities of solid ess Restitution of coefficient ? Internal friction angle Ps Solid pressure CD Drag coefficient Re Reynolds number Vr,s Terminal velocity of solid phase

References

[1] Baha Abulnaga, P.E., 2021. Slurry systems handbook. McGraw-Hill Education. [2] Hsu, T.J., Jenkins, J.T. and Liu, P.L.F., 2003. On two?phase sediment transport: Dilute flow. Journal of Geophysical Research: Oceans, 108(C3). [3] Schramm, L.L., 2006. Emulsions, foams, and suspensions: fundamentals and applications. John Wiley & Sons. [4] Peker, S.M. and Helvaci, S.S., 2011. Solid-liquid two phase flow. Elsevier. [5] Albion, K.J., Briens, L., Briens, C. and Berruti, F., 2011. Multiphase flow measurement techniques for slurry transport. International Journal of Chemical Reactor Engineering, 9(1). [6] Bahadur, S. and Badruddin, R., 1990. Erodent particle characterization and the effect of particle size and shape on erosion. Wear, 138(1-2), pp.189-208. [7] Desale, G.R., Gandhi, B.K. and Jain, S.C., 2006. Effect of erodent properties on erosion wear of ductile type materials. Wear, 261(7-8), pp.914-921. [8] Singh, G., Kumar, S. and Sehgal, S.S., 2018. Taguchi approach to erosion wear optimization of WC-10Co-4Cr sprayed austenitic steel subjected to equisized slurry. Industrial Lubrication and Tribology. [9] Deng, T., Bingley, M.S. and Bradley, M.S., 2004. The influence of particle rotation on the solid particle erosion rate of metals. Wear, 256(11-12), pp.1037-1049. [10] Heilbronner, R. and Keulen, N., 2006. Grain size and grain shape analysis of fault rocks. Tectonophysics, 427(1-4), pp.199-216. [11] Gupta, R., Singh, S.N. and Sehadri, V., 1996. Prediction of uneven wear in a slurry pipeline on the basis of measurements in a pot tester. International Journal of Multiphase Flow, 22(S1), pp.152-152. [12] Desale, G.R., Gandhi, B.K. and Jain, S.C., 2006. Effect of erodent properties on erosion wear of ductile type materials. Wear, 261(7-8), pp.914-921. [13] Gupta, R., Singh, S.N. and Sehadri, V., 1995. Prediction of uneven wear in a slurry pipeline on the basis of measurements in a pot tester. Wear, 184(2), pp.169-178. [14] Kumar, R., Bhandari, S. and Goyal, A., 2017. Slurry erosion performance of high-velocity flame-sprayed Ni-20Al2O3 and Ni-10Al2O3-10TiO2 coatings under accelerated conditions. Journal of Thermal Spray Technology, 26(6), pp.1279-1291. [15] Round, G.F. and Hessari, A.R., 1987. Rheology of coal slurries, pH and size distribution effects. Particulate and Multiphase Processes, 3, pp.329-340. [16] Singh, M.K., Kumar, S. and Ratha, D., 2020. Computational analysis on disposal of coal slurry at high solid concentrations through slurry pipeline. International Journal of Coal Preparation and Utilization, 40(2), pp.116-130. [17] Singh, K.P., Kumar, A. and Kaushal, D.R., 2022. Experimental investigation on effects of solid concentration, chemical additives, and shear rate on the rheological properties of bottom ash (BA) slurry. International Journal of Coal Preparation and Utilization, 42(3), pp.609-622. [18] KALYANARAMAN, K. and AJ, R., 1973. CHARACTERISTICS OF SAND-WATER SLURRY IN 90OHORIZONTAL PIPE BENDS. [19] Turian, R.M., Ma, T.W., Hsu, F.L., Sung, M.J. and Plackmann, G.W., 1998. Flow of concentrated non-Newtonian slurries: 2. Friction losses in bends, fittings, valves and venturi meters. International journal of multiphase flow, 24(2), pp.243-269. [20] Bozzini, B., Ricotti, M.E., Boniardi, M. and Mele, C., 2003. Evaluation of erosion–corrosion in multiphase flow via CFD and experimental analysis. Wear, 255(1-6), pp.237-245. [21] Mansouri, A., Arabnejad, H., Shirazi, S.A. and McLaury, B.S., 2015. A combined CFD/experimental methodology for erosion prediction. Wear, 332, pp.1090-1097. [22] Njobuenwu, D.O. and Fairweather, M., 2012. Modelling of pipe bend erosion by dilute particle suspensions. Computers & Chemical Engineering, 42, pp.235-247. [23] Ito, H., 1960. Pressure losses in smooth pipe bends. [24] Kaushal, D.R., Kumar, A., Tomita, Y., Kuchii, S. and Tsukamoto, H., 2013. Flow of mono-dispersed particles through horizontal bend. International Journal of Multiphase Flow, 52, pp.71-91. [25] Drew, D.A., Lahey, R.T., 1993. Particulate Two – Phase Flow. Butterworth-Heinemann Publications, Boston, pp. 509–566. [26] Drew, D.A., 1982. Mathematical modeling of two-phase flow. WISCONSIN UNIV-MADISON MATHEMATICS RESEARCH CENTER. [27] Lun, C.K.K., Savage, S.B., Jeffrey, D.J. and Chepurniy, N., 1984. Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. Journal of fluid mechanics, 140, pp.223-256. [28] Gidaspow, D., Bezburuah, R. and Ding, J., 1991. Hydrodynamics of circulating fluidized beds: kinetic theory approach (No. CONF-920502-1). Illinois Inst. of Tech., Chicago, IL (United States). Dept. of Chemical Engineering. [29] Schaeffer, D.G., 1987. Instability in the evolution equations describing incompressible granular flow. Journal of differential equations, 66(1), pp.19-50. [30] Syamlal, M., O\'Brien, T.J., Benyahia, S., Gel, A. and Pannala, S., 2008. Open-source software in computational research: a case study. Modelling and simulation in engineering, 2008. [31] Richardson, J.R., Zaki, W.N., 1954. Sedimentation and fluidization: Part I. Trans. Inst.Chem. Eng. 32, pp 35–53. [32] Garside, J. and Al-Dibouni, M.R., 1977. Velocity-voidage relationships for fluidization and sedimentation in solid-liquid systems. Industrial & engineering chemistry process design and development, 16(2), pp.206-214. [33] Launder, B.E. and Spalding, D.B., 1972. Lectures in mathematical models of turbulence. [34] Yakhot, V. and Orszag, S.A., 1986. Renormalization group analysis of turbulence. I. Basic theory. Journal of scientific computing, 1(1), pp.3-51. [35] Choudhury, D., 1973. Introduction to the renormalization group method and turbulence modeling. Fluent incorporated. [36] Schaan, J., Sumner, R.J., Gillies, R.G. and Shook, C.A., 2000. The effect of particle shape on pipeline friction for Newtonian slurries of fine particles. The Canadian Journal of Chemical Engineering, 78(4), pp.717-725. [37] Kaushal, D.R. and Tomita, Y., 2002. Solids concentration profiles and pressure drop in pipeline flow of multisized particulate slurries. International journal of multiphase flow, 28(10), pp.1697-1717. [38] Launder, B.E. and Spalding, D.B., 1972. Lectures in mathematical models of turbulence. [39] Yakhot, V. and Orszag, S.A., 1986. Renormalization group analysis of turbulence. I. Basic theory. Journal of scientific computing, 1(1), pp.3-51. [40] Choudhury, D., 1973. Introduction to the renormalization group method and turbulence modeling. Fluent incorporated. [41] Schaan, J., Sumner, R.J., Gillies, R.G. and Shook, C.A., 2000. The effect of particle shape on pipeline friction for Newtonian slurries of fine particles. The Canadian Journal of Chemical Engineering, 78(4), pp.717-725. [42] Kaushal, D.R. and Tomita, Y., 2002. Solids concentration profiles and pressure drop in pipeline flow of multisized particulate slurries. International journal of multiphase flow, 28(10), pp.1697-1717.

Copyright

Copyright © 2023 Sai Swapnesh Mishra, Kalpanta Mahapatra. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.