Effects of Interference of Hill on Wind Flow around Tall Buildings Situated in Hilly Region Using CFD

Abstract

The location of tall building in complex region, wind is the powerful factor exerted on tall buildings. This pressure has a direct affected on the drag force. The drag force has a significant impact on the building\\\'s surface. All the faces of a tall building\\\'s drag force or maximum pressure coefficient have generally been measured through wind tunnel experiments. It\\\'s difficult and costly, but it\\\'s the best option. Computational Fluid Dynamics (CFD) has been used in this study to determine the external pressure coefficient on the front and back sides of a tall building in the presence of hill interference in complex region. In addition, the current research investigates the behaviour of wind flow around tall buildings at different location of hill first scenario the top of a hill, second scenario the front and third scenario back zones of a hill, and the interactions between tall buildings and the hill itself.

Introduction

I. INTRODUCTION

Growing populations, scarcity of land, and hence rising property costs, especially in metropolitan areas, necessitate the development of taller constructions. People are migrating from cities to rural regions as a result of the growing population and land constraints in cities. Tall buildings on flat terrain are appropriate in rural locations where the wind profile is well established and the behaviour of structures under wind stimulation is well investigated. As this region grew less suitable for agricultural use, the construction of more complicated terrain regions, such as those with hills or undulating terrain, would be necessary. Because hills cannot be utilised for agriculture, their effect on existing constructions may be beneficial. High rises, on the other hand, are rarer in urban centres, where they are often seen as part of a tall building. A similar scenario may arise in hilly locations in the near future. It is significant to observe that the wind force acting on tall main buildings differs greatly from the wind force acting on a single building. Because of the elevation of the hill, interfering buildings in close vicinity alter the wind flow patterns around main buildings.

Tall buildings are vulnerable to increased or decreased wind pressure as the flow speed increases at the top of the hill, which may cause structural damage. Changing wind patterns around tall buildings can lead to major problems at the top of a hill. When tall buildings on top of a hill, lateral forces, particularly wind loads, must be addressed. Flow separation and recirculation may cause issues on the hills' leeward sides. Understanding the impacts and challenges of hill influence is critical for making better judgements. Interference mechanisms are impacted by hill shape and size, topographical changes, the size and shape of tall structures, and the closeness of interfering objects to one another. The optimum distance between the interfering and principal tall buildings is being researched in depth to minimize turbulence generated by the interfering building at the top of the hill. The interfering and principal buildings of the symmetrical bluff bodies on top of the hill have the same square cross-section. Computational Fluid Dynamics (CFD) is used to compute the wind flow around a row of two buildings with a wind incidence angle of 0°.

II. DESCRIPTION OF SIMULATION

A. Geometry configuration of tall building model in context with hill.

An 85-meter-high bluff body with full size proportions of height “H”, length “l”, and breath “B” of 30 meter was used for this research of tall buildings under the influence of hills. The distance between the hill and the tall building was varied from 1.5Le, Le, 0.75Le and 0.5Le at front region and rear region of the tall building for the research study in order to evaluate the wind pressure coefficient on the tall building while there is an interference condition of hill as shown in Fig. 1(a) and 1(b).

Specially, the simulation approach known as computation fluid dynamics (CFD) is used to analyse the wind pressure and the behaviour of the wind flow affected by the interference condition caused by the hill at various location in relation to the tall building for wind incidence angle 0°.

C. Details of Domain and Meshing

The investigation domain should be sufficiently large to avoid fluid flows from reflecting and generating an improper pressure field around the tall building in relation to the hill. Franke et al. [3] and Revuz et al. [4] selected the domain size for this analysis, which was used in their research. Figure 1(a) and 1(b) show that the domain has a “5H” upstream side from the foot of a hill and/or the front face of a tall building, a “15H” downstream side from the tall building back face and/or foot of the hill, and a “5H” side and top clearance from both top of the hill/tall building and foot of the hill, respectively.

A. Solver Setting

All of the outcomes were steady-state in nature. Second-order differencing was used for the pressure, momentum, and turbulence equations, as well as the "coupled" pressure-velocity coupling approach, which is more durable for steady-state, single-phase flow problems. After many hundreds of trials, the residuals dropped below the commonly accepted 10-4 limit. During the simulation, the drag force and average pressure value impacting on the tall structure were measured, and the simulations were regarded to have converged only when they reached stable and constant values. Even though the simulations were steady-state, the "stable" values of the continuous monitoring data ranged by around 1%. In ANSYS Fluent 2020 R1, both buildings were considered as a bluff body (a body that is angular but not aerodynamic in form), and the flow pattern around the isolated square shape building and under the interference condition due to the hill were analysed under various conditions. Table – 5 of IS: 875 (Part 3), 2015 [2] contains the external pressure coefficient (Cpe). Following the fulfilment of certain requirements, the value of the external pressure coefficient is examined. It has been determined that the requirement 3/2 < h/w < 6, 1 < l/w ≤ 1/2 is fulfilled with Table: 4 of IS: 875 (Part 3), 2015 [2] in this research. Where "H" denotes the bluff body’s height above mean ground level, "w" denotes the width or smaller horizontal dimension of a bluff body, and "l" is denoting the length or larger horizontal dimension of a bluff body, as defined in IS: 875 (Part 3), 2015 [2] for the examination of the reliability of the software.

TABLE III

B. Examination of the reliability of ANSYS Fluent Software based on a comparative analysis of the findings of a square shape building model

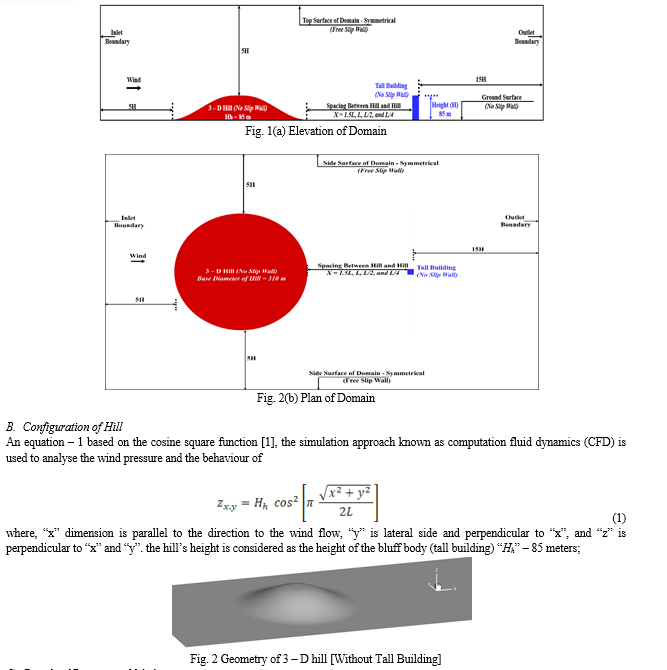
As illustrated in Fig. 5, the pressure distribution on different faces of a square-shaped building model with an aspect ratio “h/w” considered 3 for the reliability of software for wind incidence angles of 0° is presented on different faces of the square shape building model. Pressure on the windward face is positive, as expected, with the highest pressure in the center of the windward facing area. Moreover, since wind flow displays symmetry, pressure distribution is symmetrical around the vertical centerline. In addition, there is a thin line of significant negative pressure towards the windward face, which causes suction on the side faces. This is caused by the flow being separated from the edges of the windward face. Because of the symmetry of wind flow, the pressure distributions on the two side faces are identical. On the leeward face, suction is also present; however, this time, the pressure is equally distributed along the horizontal line. As shown in Table 3, the findings obtained for the square model are compared with those accessible in the IS: 875 (Part 3), 2015 [2], which are included in the IS: 875 (Part 3), 2015 [2] and value published by the researcher found by the wind tunnel experimental.

The wind pressure was evaluated with the wind incidence angle set to 0° on the windward and leeward faces of the tall building, the mean pressure was measured at the windward and leeward faces. In addition, maximum pressure values were determined for each face of the tall building, and the drag coefficient was computed at different positions along the tall building's length in respect to the hill. By using the Equation 7, we were able to convert these pressures into pressure coefficients, which is a dimensionless number that reflects how pressure is distributed on all side faces of a tall building and varies based on the tall building's location in reference to a 3-dimensional hill.

The investigation of the square shape building model included the analysis of a principal building in an isolated condition in ANSYS Fluent 2020 R1 in order to verify its acceptability and reliability in assessing pressure coefficient in accordance with the IS: 875 (Part 3), 2015 [2], and value published in research paper.

The findings show that the ANSYS Fluent 2020 R1 has a high degree of consistency, with the results being pretty close to the IS: 875 (Part 3), 2015 [2] prescribed values of pressure coefficients as well as result published by the researcher in research paper shown in Table 3. As a result, the data considered for the principal building in isolated condition can be used to evaluate the pressure coefficient under the interference condition of hill in a complex region for different spacing ratios between the hill and the square shape building using the ANSYS Fluent 2020 R1 software. This allows for the necessary investigation.

TABLE IIIII

IV. RESULT AND DISCUSSIONS

A. Flow analysis for a hill with no tall buildings

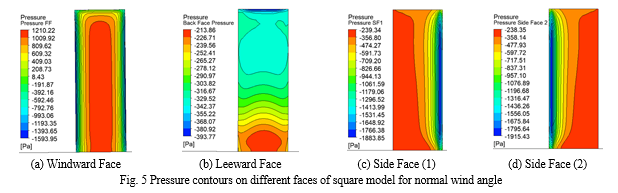
At three different locations along on the symmetrical vertical plane, wind velocity profiles are shown in Figure 6. One is at a point on the windward side of a hill, the second is on the leeward side of the hill, and finally, the third is at the top of the hill. The k – ? (Realizable) turbulence model is used in this study to calculate wind flow analysis. ANSYS turbulence model predicts velocities that are very close to the flow physics. hills without buildings have been used as a research study in this investigation. The velocity profile shown in Fig. 6 shows the wind velocity profile at three locations and higher wind is near the top of the hill's top. The maximum speed of 55.47 m/s was attained towards the top of the hill. Once at the top, the 44 m/s speed progressively reduces in a vertical direction.

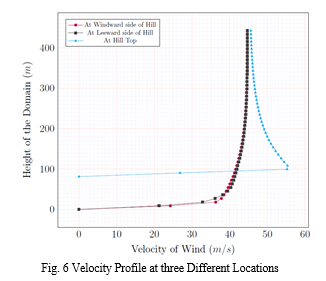
For the 85-meter-high hill in Fig. 5, the pressure contour diagram is shown on a symmetrical vertical plane at y = 0, with the wind direction taken into account from left to right. The incoming velocity of 44 m/s is uniform and progressively rises from ground level because to the thin boundary layer near the ground. As the boundary layer reaches the top of the top of the hill in Fig.7, it grows rapidly as a result of the considerable negative pressure gradient. Wind flow acceleration is only influenced in small places at the top of the hill, where the boundary layer is getting thinner, since the boundary layer is becoming increasingly thin. Generally, the top of a hill is considered a high-speed zone. After the hill, the boundary layer thickens, creating a low-speed zone behind the leeward side. Flow doesn't seem to separate on the leeward side.

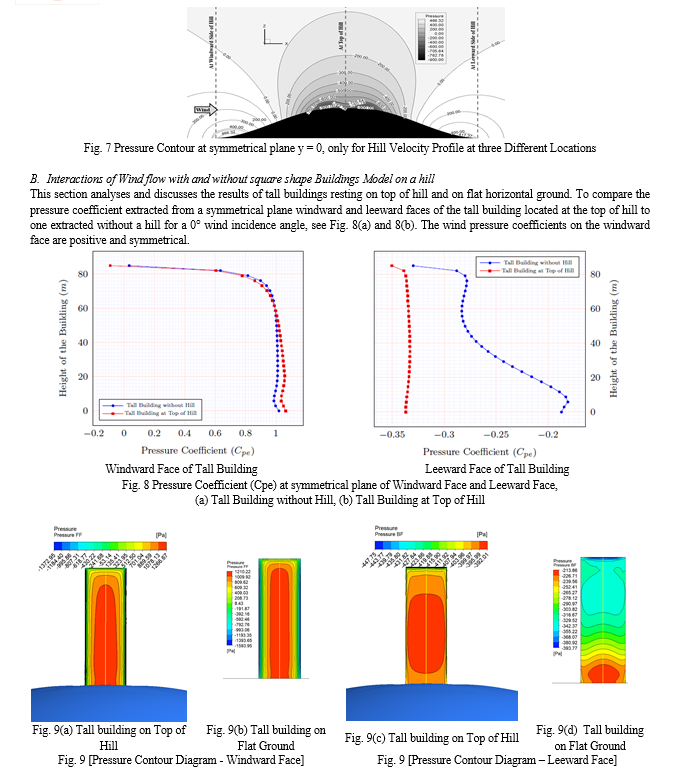
Tall buildings on a top of hill have a maximum wind pressure coefficient of 1.068, whereas tall buildings on a level terrain have a maximum wind pressure coefficient of 1.021. Pressure contour lines on the windward face indicate very different wind pressures in both circumstances, resulting to fluid separation as seen in Fig. 9(a) and 9(b). The maximum pressure coefficient on sides is -1.226 for tall buildings at the top of a hill and -1.589 for tall buildings on a level terrain, which is consistent with the symmetric arrangement in the computational domain. The formation of a vortex along the height of a structure occurs when wind blows around the side of the structure. Fig. 8(b) shows the average pressure coefficient on the leeward face of tall buildings. Fig. 9(c) and 9(d) show pressure contours on a leeward face with and without a hill. The highest-pressure coefficient is -0.378 on the top of hill, indicating a high-pressure area due to wind recirculation and the hill's blocking effect; the lowest pressure coefficient is -0.332 on flat terrain, indicating a low-pressure area.

C. Interaction of Flow with Tall Building, when Hill Positioned at 1.5L, L, 0.75L, and 0.5L Wake Region of Tall Building on Flat Terrain, at top of hill and tall building without hill.

This section shows the pressure coefficient values on the windward and leeward faces of the tall building with a hill at 1.5L, L, 0.75L, and 0.5L from the tall building's wake region at a 0° wind incidence angle. They are compared to the pressure coefficient at a symmetrical plane passing through a tall building position without a hill (on level horizontal ground) and at the top of a hill, as illustrated in Fig. 10(a) and 8(b). For tall buildings that are symmetrically placed (y=0), it is feasible to get almost the same value and a positive pressure coefficient when the building is directly impacted by wind on its windward face. The hill's position with respect to the tall building's wake region (1.5L, L, 0.75L, and 0.5L), as well as the fact that it is not a significant obstruction in the path of the wind, makes it an effective windbreak. As a consequence, the value of the pressure coefficient at the symmetrical plane is practically the same on the windward face of the tall building at the top of the hill as the value of the pressure coefficient on the windward face of the tall building without hill (on flat level ground). Near the surface of the earth, there is only a little variance in pressure readings. For 1.5L, L, 0.75L, and 0.5L, the drag coefficient ranges between 0.466, 0.566, 0.838, and 0.854 and that is depending on the distance of the hill at the wake region of a tall building, and is 0.792 and 1.052 for flat level ground and at the top of the hill, respectively. The effect of the presence of the hill on windward face of tall building not affected as wind is impacted directly on windward face when the distance of the hill varies from 1.5L to 0.5L but the wind flow affected on leeward face of the tall building only due to the blockage or obstruction of the hill at wake region when the hill is very nearer to the tall building.

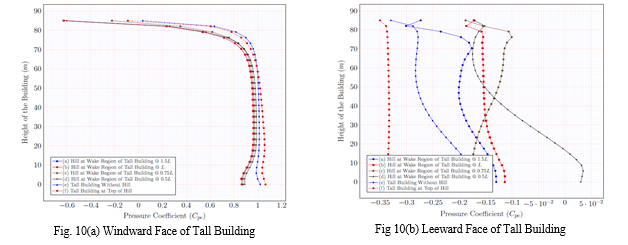
leeward face of a tall building has a negative pressure coefficient for all case of hill’s position at wake region of the tall building at 1.5L, L, 0.75L, and 0.50L and for tall building at top of the hill and the without hill as there is no any kind of an obstruction to the wind flow. As shown in Fig. 10(b), the value of the pressure increases (in terms of negative) when the tall building is located at the top of a hill due to recirculation of the wind flow at the wake region, which is more pronounced in this case due to the hill height than when the tall building is located on a flat level surface. As shown in Fig. 10(b), the value of the pressure coefficient decreases when the spacing of the hill is reduced from 1.5L to 0.5L at the wake region of the tall building and is converted to a positive value nearer to the ground when the distance of the hill is at 0.5L due to obstruction or blocking of the wind flow at the wake region.

D. Interaction of Flow with Tall Building, when Tall Building Positioned at 1.5L, L, 0.75L, and 0.5L Wake Region of Hill on Flat Terrain, at top of hill and tall building without hill.

This section shows the pressure coefficient values on the windward and leeward faces of the tall building with a hill at 1.5L, L, 0.75L, and 0.5L from the tall building's windward region for a 0° wind incidence angle. They are compared to the pressure coefficient at a symmetrical plane passing through a tall building position without a hill (on level horizontal ground) and at the top of a hill, as illustrated in Fig. 11(a) and 11(b). According to the observation, when tall structures are symmetrically arranged (y=0), it is possible to get a lower and more positive value of the pressure coefficient when the tall building is located at a distance of 1.5L from the wake region of the hill. It is feasible because of the recirculation of the flow and the generation of the vortices in the wake zone of the hill, which decreases the pressure coefficient on the windward face of the tall building on the windward region of the building. However, when the distance between the hill and the tall building is reduced up to 0.5L, the value of the pressure coefficient increases. Because of the shear flow that reattached at the wake region of the hill and wind flow directly impacted on the windward face of the tall building at smaller distances of L, 0.75L, and 0.50L same scenario happed in situation of the tall building at the top of the hill and or on flat level ground.

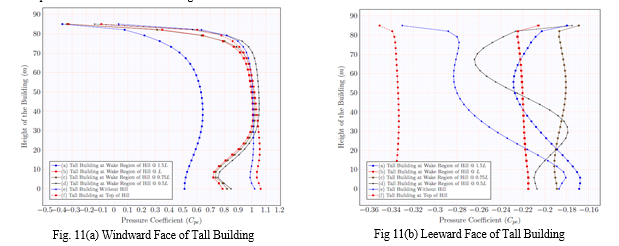
There is a change in pressure on the windward side of the tall building, especially at the pedestrian level. This is because of the shear flow separation caused by the side of the hill at ground level and the large amount of wind moving in the wake region of hill at ground level, which causes vortices at the 0.1H to 0.15H height at the ground level and developed low pressure zone and due to this reduced the pressure coefficient at pedestrian level. The value of drag coefficient ranges between 0.601, 0.650, 0.833, and 1.080 and that is depending on the distance of the tall building at the wake region of a hill, and is 0.792 and 1.052 for flat level ground and at the top of the hill, respectively. The effect of the hill interference on wind flow for 0° wind incidence angle on leeward face of tall building more affected as shear flow separation from the sides of the tall building, which causes a low – pressure zone at wake region of the tall building. By decreasing the distance between hill and the tall building from 1.5L to 0.50L, enormous vortices are generated. Large, stable vortices formed when there are decreases the distance between hill and the tall building due to the shorter distance and flow separated from the corners of the tall building.

Conclusion

The basic k ? ? (Realizable) turbulence model was used for simulation to investigate the influence of wind flow on tall buildings in various position in the context of a 3-dimensional hill. The pressure value on two faces of the tall structure, as well as variations in wind flow and wind flow behaviour surrounding tall structures, were investigated. The key findings of the study may be summed up in a list. 1) The presence of the hill has no effect on the windward face of the tall building because the wind is impacted directly on the windward face when the distance between the hill and the tall building varies from 1.5L to 0.5L, but the wind flow on the leeward face of the tall building is affected only because the hill is blocking or obstructing the wind flow in the wake region when the hill is very close to the tall building. 2) The drag coefficient for tall buildings at the top of a hill rises from 0.79 to 1.05 as the hill\\\'s height rises above level ground. 3) The highest-pressure coefficient is produced on the windward and leeward faces of a tall building when it is positioned extremely close to the hill on the windward and leeward sides, and this is possible due to the obstruction of wind velocity and change in wind flow patterns in both the cases. 4) The pressure value on the windward face of the tall building remained unchanged and was the same as before the hill, but the pressure value on the leeward face of the tall structure increased, which was dependent on the height of the hill. 5) In all cases, the flow on the leeward side of the tall building is more sensitive to the tall building (i.e.L/4 = 77.5 m). However, there is a very tiny amount of change in wind flow and effects on tall buildings at the large spacing (i.e.1.5L = 465 m). 6) The drag coefficient of a tall building achieves a maximum of 1.08 when the tall building is located in the leeward side of the hill, and a value of 0.85 when the tall building is placed on the windward side of the hill, according to an examination of the drag coefficient of a tall structure by dropping the spacing from 1.5L to 0.25L. 7) Because of the increased disturbing effect of the 3-dimensional hill on the leeward side of the tall building, the downwind side of the tall building may also generate flow separation on the windward side of the 3-dimensional hill with smaller spacing. The hill has clearly disrupted the flow of traffic around tall buildings in a hilly site. 8) The influence of wind flow on the design of a tall building in a hilly site must be considered while planning and designing it.

References

[1] Yan, Shu, Shaoping Shi, Xinming Chen, Xiaodong Wang, Linzhi Mao, and Xiaojie Liu. \\\"Numerical simulations of flow interactions between steep hill terrain and large-scale wind turbine.\\\" Energy 151 (2018): 740-747. [2] IS 875 (Part 3), Indian Standard code of practice for design loads (other than earthquake) for building and structures, Bureau of Indian standard, New Delhi, 2015. [3] Franke, J., Ch Hirsch, A. G. Jensen, H. W. Krüs, M. Schatzmann, P. S. Westbury, S. D. Miles, J. A. Wisse, and N. G. Wright. \\\"Recommendations on the use of CFD in predicting pedestrian wind environment.\\\" In Cost action C, vol. 14. 2004. [4] Revuz, Julia, D. M. Hargreaves, and J. S. Owen. \\\"On the domain size for the steady-state CFD modelling of a tall building.\\\" Wind and structures 15, no. 4 (2012): 313. [5] Amin, J. A., and A. K. Ahuja. \\\"Effects of side ratio on wind-induced pressure distribution on rectangular buildings.\\\" Journal of Structures 2013 (2013). [6] B. Blocken, Computational fluid dynamics for urban physics: importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations, Build. Environ. 91, 219 – 245 (2015) [7] A. Mochida, Y. Tominaga, S. Murakami, R. Yoshie, T. Ishihara, R. Ooka, Comparison of various k-e models and DSM applied to flow around a high-rise building-report on AIJ cooperative project for CFD prediction of wind environment, Wind Structures, 5, 227-244 (2002) [8] J. Hang, M. Sandberg, Y. Li, Effect of urban morphology on wind condition in idealized city models, Atmos. Environ, 43, 869 – 878 (2009) [9] W.D. Janssen, B. Blocken, T. van Hooff, Pedestrian wind comfort around buildings: comparison of wind comfort criteria based on whole-flow field data for a complex case study, Building Environments, 59, 547 – 562 (2013) [10] D.B. Spalding, B.E. Launder, The numerical computation of turbulent flows, Computer Methods in Applied Mechanics and Engineering, 3, 269 – 289 (1974) [11] Mehta, Kamlesh, and Jigar Sevalia. \\\" Effectiveness of CFD simulation of wind flow & its effect on tall structures with aerodynamic shapes.\\\" International Journal of Advanced Research in Engineering and Technology (IJARET), 11(12) (2020); 2437–2446. [12] ANSYS Inc. (US), ANSYS Fluent Theory Guide, Release 14, 724 – 746 (2013) [13] Avramenko, A., Agafonova, O., Sorvari, J., & Haario, H., Simulation of depth-integrated flow over a hill, AIP Conference Proceedings 1738, 480082 (2016) [14] Prigent, C., I. Tegen, F. Aires, B. Marticore´na, and M. Zribi. Estimation of the aerodynamic roughness length in arid and semiarid regions over the globe with the ERS scatter meter. Journal of Geophysical Research: Atmospheres, 110 (D9), 1–12 (2005)

Copyright

Copyright © 2023 Kamlesh Mehta, Dr. Jigar Sevalia. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.