Exploratory Data Analysis and Forecasting the Output Power Generated by Solar Photovoltaic

Abstract

Due to solar PV panels\' growing feasibility as a renewable energy source, PV panel installations have surged recently. Machine learning algorithms can now generate better predictions due to the increasing availability of data and computing capacity. For many stakeholders in the energy business, predicting solar PV energy output is crucial, therefore machine learning and time series models may be used to do this. In this study, time series models and several machine learning techniques are compared across five different sites in India. Since the energy time series are non-stationary, we find that applying time series models is a challenging process. On the other hand, putting machine learning methods into practice was simpler.

Introduction

I. Introduction

The development of photovoltaic (PV) panels has been influenced by the global drive toward renewable energy sources (RES). For instance, as energy conversion efficiency has increased, the cost of producing power from PV panels has significantly decreased. More particular, between 2010 and 2017 [1], the levelized cost of electricity for large-scale PV panels reduced by 73%. PV panels are becoming more and more recognized as a viable RES alternative because of their lower cost and improved efficiency [2]. However, because it is impacted by outside factors like cloud cover and sunshine, the energy production of the PV panels is unreliable. Many stakeholders in the energy industry place priority on comprehending and managing output unpredictability. A transmission system operator is interested in the energy output from Pv system in the near term (0–5 hours) to determine the proper careful balance for the entire grid since producing too much or too little power typically carries fines. On the other end of the spectrum, because the majority of energy is traded on the day-ahead market, electricity traders are interested in extended time horizons, typically day-ahead predictions. Therefore, the capacity to accurately forecast the variable solar PV panel energy output is necessary for these operations to be profitable. Solar PV panel use is projected to rise as more nations choose to spend more and more in RES. As a result, reliable methods for predicting solar PV energy generation will become more important. Despite the clear need for precise and trustworthy estimates of PV panel energy output, a solution is tough to come by. The topic's current study includes overcoming a variety of challenges. The weather's natural tendency to fluctuate is one evident annoyance that makes accurate weather forecasting difficult... The capacity to anticipate utilizing machine learning (ML) approaches has recently grown in popularity as compared to conventional time series predictive models, which is parallel to the rise in demand for PV power forecasting. The availability of high-quality data and improvements in processing power have made ML techniques—which are not new—useful for prediction. When calculating the amount of solar power produced, the following is an intriguing topic to research: When compared to established methods, how successful are machine learning approaches for time series forecasting?

II. Objectives

The main goal is to compare several methods for predicting energy production from solar PV panels. This may be accomplished by dynamically understanding the link between various weather conditions and the energy production of PV systems using machine learning and time series approaches. Using information from existing PV system installations, four ML algorithms are contrasted with conventional time series methods. Additionally, feature engineering has to be considered in this.

III. Literature review

Andrade et al. [2], investigated and assessed ML approaches in conjunction with creating features that were intended to enhance performance. Principal Component Analysis (PCA) and a feature engineering methodology in conjunction with a Gradient Boosting Tree model were the key methodologies used in the study. Additionally, the authors created features from their NWP data using several smoothing techniques.

Dav et al. [10] coupled PCA with the ANN and Analog Ensemble (AnEn) approaches. PCA was applied as a feature selection technique with the goal of reducing the dataset's dimensionality. The dataset consists of the total daily solar radiation energy production that was measured over an eight-year period. When compared to not utilizing PCA, it was found that employing PCA in conjunction with ANN and AnEn improves prediction accuracy.. Results on long-term (up to 100 hours) forecasting are presented by Chen et al. With NWP data as input, the authors used an ANN as their forecasting method. The model was susceptible to the NWP input data's prediction mistakes, and it also displayed degradation while forecasting, particularly on rainy day

IV. Methodology

We outline the methods for this thesis in this chapter. We talk about the initial data, where it came from, and how it was organized. The chapter will go on to talk about the data processing that was done, as well as a clear explanation of what was done for the. various time series and ML approaches

R version 3.4.3 [20] and RStudio [21] have been used for all data processing and mathematical computation during the whole project. Caret [22], a wrapper comprising tools for expediting the building of predictive models and pre-processing data, is the primary R package used.

A.  Raw Data

1. Power Data

The information on energy output was gathered using installations of small-scale solar PV panels with a peak power range of roughly 20kW to 150kW. Additionally, about two to three years ago, data on energy output was gathered at five distinct locations in India at intervals of 15 minutes.

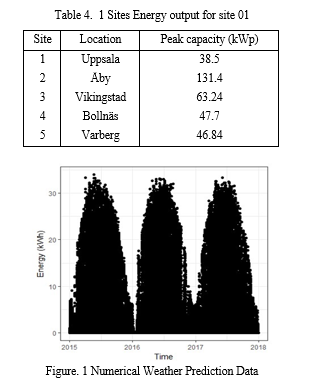
The five different sites' weather data were derived from Meteomatics [23]. The retrieved data parameters, along with a brief explanation and the associated units, are listed in table 4.2. For a deeper explanation of meteorological variables and their corresponding definition, see [23].

B. Variability in Data

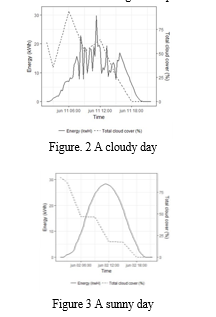
The output from a particular PV panel varies greatly, as seen in figures 4.2 and 4.3, thus the projection of the total cloud cover is inaccurate. It is highlighted by the fact that two reasonably similar forecasts can result in reasonably differing actual energy output levels. Significant global mistakes can be formed when local forecasting technique faults combine with local input data problems..

C. Data Processing

In general, the data have been relatively clean. As a result, the main part of the data processing is related to sorting the data in the right way. The datasets were filtered by computing a lead time for when data was available in real time. The dataset was sorted for this lead time so that no dataset contained unavailable information.

When the data was sorted correctly, a data row consisted of the corresponding NWP data and lagged variables. It should be clarified that when a prediction on any time horizon is performed, it refers to forecasting the energy output of a 15-minute interval in that time horizon and not the energy output of the next time step. A prediction for an hour therefore refers to the energy output of 15 minutes within an hour rather than the energy output of the hour that will follow.

Measures would be inflated and present an inaccurate image of the performance of the models. Additionally, incorporating nighttime data would force the model to choose between adequately fitting daytime data and nighttime data, the latter of which is meaningless. Any observation with clear sky radiation of more than 10 W/m2 was assumed to be during the day because the length of the night changes in India depending on the seasons.

D. Outlier Handling

To find outliers, a visual assessment was conducted. Power outputs that are negative or above the installation's max capacity could serve as an illustration. An observation is expected to be comparable to the 15-minutes ahead and 15-minute lagged observations because all the data are provided at 15-minute intervals. So, a value that is interpolated between the prior and next observations is regarded as a reliable estimate.

E.  Feature Engineering

1. Lagged Output

The lagged output value will be crucial for making predictions over short time horizons. If the sky was clear for the last 15 minutes, it is likely that the sky will remain clear for the ensuing 15 minutes as well. The output at the same time the day before is a better approximation for output for longer forecast horizons because it is one day behind. Because of this, we incorporate the one-step, two-step, and one-day lagged output variables into the models along with the difference between them. One-step refers to the level of granularity of the data (15 minutes).

The variables are built as follows if yt is the output at time t:

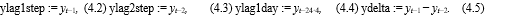
F. Temporal Weather Grid

Inspired by the results of Bessa and Andrade [2], a feature engineering process was performed as an attempt to create features that could enhance the performance. A temporal grid and temporal variability for the features are computed. As the NWP variables are forecasted for the ZIP code, and not the exact coordinates of the specific site, one can assume that the 15-minute lagged and lead forecasts have predictive ability. Then, if NWPi,t is the forecast of NWP variable i at time t, the lagged value is NWPi,t−1 and the lead value NWPi,t+1 where one time-step is 15 minutes. The grid is only performed for t ± 1, not to lose too much data.

G. Solar Zenith Angle

The zenith angle, which shows how directly the solar irradiance is pouring in, was another feature introduced. Based on the time-stamps and coordinates of the installation location for the solar PV panels, this was calculated using the SZA() function in the Atmosphere package [26].

???????H.  Cross-Validation

Optimizing hyperparameters is a requirement for many time series approaches and ML techniques. To choose the best set of hyperparameters, cross-validation (CV) is a typical technique. The k-fold is one kind of cross-validation. cross-validation This usually means splitting the set into k folds at random. According to the validation principle, one of the k folds is chosen as the test set and the remaining observations are chosen as the training set. The test set is then changed to a different fold, and the remaining dataset is used as training data in the process. A performance measure is produced for each k-fold after this is performed for all the folds.. The average performance is obtained once a performance measure has been calculated for each fold. This can be done for a number of hyperparameters to find the one whose value produces the best cross-validation performance metric. K is often chosen between 5 and 10..

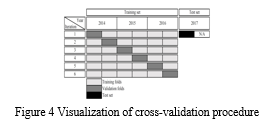
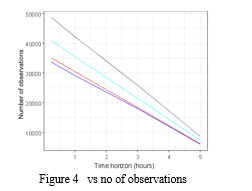
As mentioned by Hyndman et al. [28], a standard k-fold CV performs well when the data is not time-dependent. However, a standard CV procedure may be misleading when there is a considerable time dependence. Figure 4.5 provides an illustration of the actual CV technique that was used. The method is shown in the image if the data for the location were collected between January 2014 and the end of June 2017. The main presumption is that each half-year fold records a cycle of seasonal variability, which means that the patterns of energy output for January through June and July through December are essentially the same. Therefore, each half-year fold can be viewed as almost independent of the other. Only the half-year folds retain the serial correlation that makes time series difficult for regular CV. Since then, the folds must be separated in ascending order rather than at random. Although using a full one-year cycle each fold would be ideal, there wasn't enough data to do so...

???????I.  Performance Metrics

1. Algorithm

for each forecast horizon do filter data based on availability; remove nighttime observations; partition the dataset into training and test set; partition training data into k half-year folds; define a parameter set (e.g. K = (1,...,10) for KNN); for each parameter p in parameter set do for each fold i in set of K folds do use fold i as validation set; [optional] pre-process the data; fit the model on the other K − 1 folds; predict values for the validation set;

end

calculate the average RMSE on the validation sets;

choose the best hyperparameters (those with the lowest RMSE); train the model using the best hyperparameters on all training data; evaluate the model on the test set (i.e., the data from the previous six months); final

2. ARIMA

A traditional time series methodology was used to carry out the ARIMA modeling. In light of this, a test and training set was created, with the most recent half year serving as the test data and all other data serving as training data..

The validity of the ARIMA model can be questioned if any of these presumptions were broken, hence it was decided not to model the ARIMA in such circumstances. Final forecasts were computed on the various time horizons if the ARIMA model's core premise could be met.

???????K.  Lasso Regression

Feature selection is included into the method since the Lasso penalizes overfitting and reduces the values of the unimportant variables to 0. Prior to modeling using the Lasso, no apriori feature selection has been done. The updated dataset for the appropriate time spans was then sent to the glmnet function. The R package glmnet was used for the model training [31].

???????L.  Gradient Boosting Regression Trees

The model training was performed with the R package gbm [33]...

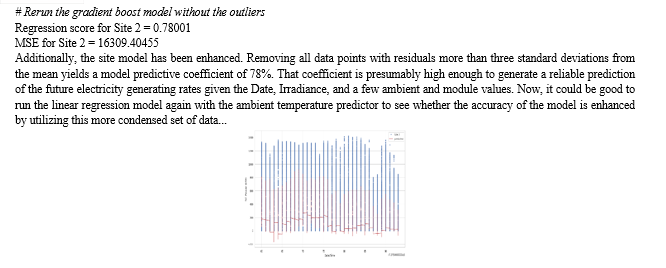
Compared to the model that used ambient temperature as its main feature, the site 1 model has significantly improved. However, the site 2 model can forecast outcomes just marginally better than a coin flip. The fact that neither of these models genuinely depends on time is another issue that has to be addressed. This adds some intrigue because it requires knowledge of the temperature in order to forecast the power output depending on that temperature. In essence, these two models set up a situation where the model's user could look at a weather forecast and enter temperatures to obtain an anticipated power. Interesting and possibly practical, but the user must take a number of steps to use it..

Additionally, because of the still-low correlation between site 2 results, Results could be improved by adopting a more complex model with more parameters. Additionally, given the data's multivariate structure, it is probably time to split the data out for time series analysis. As suggested here, we will write a function below to separate the timeseries data.

???????C. Multivariate data models

A linear regression model for the Site 1 data has again achieved a high R2R2 score.

In [29]:

# Site 2 Linear Regression Model

Although it is improved, the multivariate linear regression model for site 2 is still not very good. The data can be analyzed and cleansed for outliers, the features can be further developed to achieve better predictive capabilities, or a neural network may be needed to undertake more in-depth analysis. An attempt to improve this model can also be done (next stages). In general, it is a good idea to start with the simplest solutions and increase the complexity as necessary, thus the model will be optimized with a Grid Search Cross Validation in the next several steps. It is crucial to note that the cross-validation technique used in this case is for Time Series Splits, which may be investigated further here.:

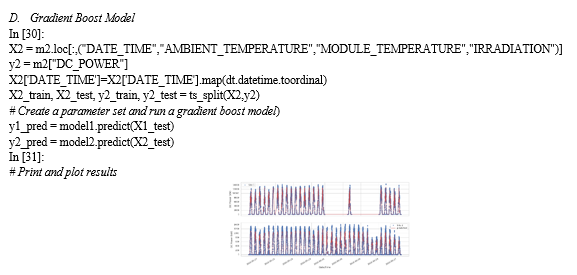
The prediction from site 1 still has a good correlation, though. The correlation of the site 2 prediction model is still just marginally better than 60%. The time series plot above demonstrates how well the gradient boosting regression matches the real DC power output pattern, but there appears to be a limit to how high the DC power prediction can be, and that is where the variance between the predicted and actual data is most obvious. The next stage is to strive to make Site 2's gradient boosting process as efficient as possible. The grid search employs a time series split to prevent unintentionally introducing stochastic randomization.

???????E. Gradient Boost Optimization

In [12]:

# Conduct optimization on gradient boost model

Well, that didn't really change the prediction at all, which is disappointing but true. Actually, there are just two possibilities left. The data can be cleaned up, or you can try a deep learning neural network. Most data cleaning will involve removing outliers, but it is also worthwhile to consider which features in the model are most crucial. It is always intriguing to use feature engineering to determine the critical variables in a collection of predictions. Since the majority of the effort to identify key features is already done, it makes sense to start there. From this point on, unless otherwise stated, everything will be in relation to the Site 2 Data.

???????

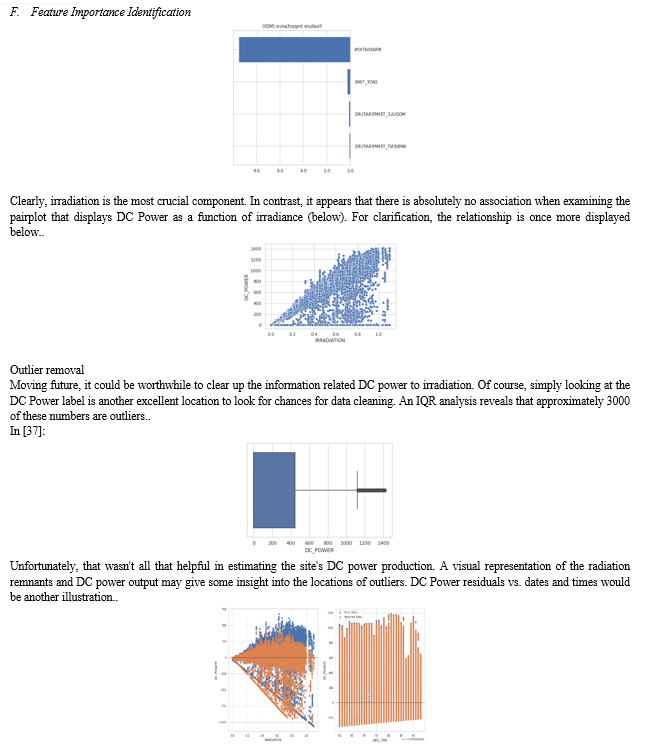
Conclusion

. In this study, we anticipate solar energy over five distinct sites in Sweden using time series methodologies and machine learning techniques. Since the energy time series are non-stationary, we find that applying time series models is a difficult undertaking. On the other hand, putting machine learning methods into practice was simpler. We discover that, on average, across all sites, Gradient Boosting Regression Trees and Artificial Neural Networks perform the best. The various models have been widely contrasted in this study. Future research should concentrate on in-depth analyses of different machine learning methodologies and use feature engineering techniques for numerical weather forecasts.

References

[1] IRENA. Renewable power generation costs in 2017. Technical report, International Renewable Energy Agency, Abu Dhabi, January 2018 [2] Jose R. Andrade and Ricardo J. Bessa. Improving renewable energy forecasting with a grid of numerical weather predictions. IEEE Transactions on Sustainable Energy, 8(4):1571–1580, October 2017. [3] Rich H. Inman, Hugo T.C. Pedro, and Carlos F.M. Coimbra. Solar forecasting methods for renewable energy integration. Progress in Energy and Combustion Science, 39(6):535 – 576, 2013. [4] J. Antonanzas, N. Osorio, R. Escobar, R. Urraca, F.J. Martinez-de Pison, and F. Antonanzas-Torres. Review of photovoltaic power forecasting. Solar Energy, 136:78–111, October 2016. [5] V Kostylev, A Pavlovski, et al. Solar power forecasting performance–towards industry standards. In 1st international workshop on the integration of solar power into power systems, Aarhus, Denmark, 2011. [6] Tao Hong, Pierre Pinson, Shu Fan, Hamidreza Zareipour, Alberto Troccoli, and Rob J. Hyndman. Probabilistic energy forecasting: Global energy forecasting competition 2014 and beyond. International Journal of Forecasting, 32(3):896 – 913, 2016 [7] Gordon Reikard. Predicting solar radiation at high resolutions: A comparison of time series forecasts. Solar Energy, 83(3):342 – 349, 2009 [8] Peder Bacher, Henrik Madsen, and Henrik Aalborg Nielsen. Online short-term solar power forecasting. Solar Energy, 83(10):1772 – 1783, 2009. [9] Hugo T.C. Pedro and Carlos F.M. Coimbra. Assessment of forecasting techniques for solar power production with no exogenous inputs. Solar Energy, 86(7):2017 – 2028, 2012. [10] Federica Davò, Stefano Alessandrini, Simone Sperati, Luca Delle Monache, Davide Airoldi, and Maria T. Vespucci. Post-processing techniques and principal component analysis for regional wind power and solar irradiance forecasting. Solar Energy, 134:327 – 338, 2016. [11] Changsong Chen, Shanxu Duan, Tao Cai, and Bangyin Liu. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Solar Energy, 85(11):2856 – 2870, 2011. [12] Caroline Persson, Peder Bacher, Takahiro Shiga, and Henrik Madsen. Multi-site solar power forecasting using gradient boosted regression trees. Solar Energy, 150:423 – 436, 2017. [13] J. Shi, W. J. Lee, Y. Liu, Y. Yang, and P. Wang. Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Transactions on Industry Applications, 48(3):1064–1069, May 2012.

Copyright

Copyright © 2022 Amir Yousuf Malik, Baljit Kaur, Zahid Mushtaq. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.