Fingerprint and Iris Compression Based on Sparse Representation for Aadhar Application

Abstract

Fingerprints and iris scans are two types of biometric identifiers that serve the purpose of identification and authentication. AADHAR is a project initiated by the Government of India that aims to provide a unique identification number to each resident in the country. Due to the complexity associated with storing these biometric identifiers, a compression technique is employed to minimize storage requirements. The study involves an analysis aimed at identifying the storage demands for biometric data in the AADHAR project. Additionally, a proposed approach that utilizes the K-SVD algorithm, based on sparse representation, is presented to considerably decrease the storage space necessary for storing fingerprints and iris scans.

Introduction

I. INTRODUCTION

The technology of biometric identification, which utilizes unique biological characteristics of individuals, is significant in modern society. Among various biometric recognition technologies, fingerprint and iris recognition are prevalent due to their distinctiveness, universal applicability, and consistency[1]. In recent years, the utilization of compression techniques in Aadhaar application has been extensively researched. Several research studies have been carried out to evaluate the efficiency and efficacy of compression techniques. These studies have shown that these techniques are highly effective in reducing the size of biometric data while maintaining their accuracy and quality, making them a suitable option for implementation in Aadhaar applications.

The compression of fingerprint and iris images is a crucial method for addressing the issue of storage space[4]. There are two main types of compression technologies: lossless and lossy. Lossless compression methods allow for the reconstruction of the original images from the compressed data without losing any information. Lossless compression techniques are used in situations where it is critical that the original data and the uncompressed data are exactly the same.

In the compression of fingerprint and iris images, compression efficiency may be limited by the requirement to avoid distortion. Lossless compression technologies are frequently utilized when slight distortion is tolerable, such as in image compression. In such cases, lossless compression is implemented on the output coefficients of lossy compression. On the other hand, lossy compression techniques typically involve transforming an image into another domain, quantizing its coefficients, and encoding them.In the past thirty years, there has been substantial research dedicated to transform-based image compression technologies, with the Discrete Cosine Transform (DCT) [2] and the Discrete Wavelet Transform (DWT) [3] emerging as the prevailing transformations in this field. The DCT-based encoder is utilized to compress an image stream comprising small 8x8 blocks and is an integral part of the popular JPEG compression scheme. However, the performance of the JPEG scheme[6] is unsatisfactory at low bit-rates due to its underlying block-based DCT scheme, despite its simplicity, universality, and widespread availability.In an attempt to overcome this limitation, the JPEG committee initiated the development of  a novel compression standard for still images, named JPEG 2000, was introduced, employing wavelet-based techniques in 1995. The DWT-based algorithms in JPEG 2000 involve three primary steps: The process of DWT computation on the normalized image, followed by quantization of the DWT coefficients, and ultimately lossless coding of the quantized coefficients, forms the foundation of JPEG 2000 [5]. In contrast to JPEG, this advanced compression standard offers a range of advantageous features that enable flexible and interactive access to large-sized images. These features encompass the capability to extract varying resolutions, pixel fidelities, regions of interest, components, and more. Various algorithms based on DWT have been developed for general image compression, including SPIHT. Despite the development of JPEG 2000, fingerprint images require special compression algorithms[8]such as Wavelet Scalar Quantization (WSQ) due to their unique characteristics. However, these algorithms have a common limitation in that they lack the ability to learn and adapt to different types of fingerprints and environments. The present paper introduces a new approach that is based on sparse representation, which can update the dictionary and compress fingerprint images effectively. The proposed method includes several steps, starting with constructing a base matrix that has columns representing various features of fingerprint images.

The fingerprint is then divided into small patches, and coefficients are obtained through sparse representation. These coefficients are then quantized and subsequently encoded using lossless coding methods.In many cases, Currently, the evaluation of compression performance is primarily limited to measuring the Peak Signal-to-Noise Ratio (PSNR), neglecting the examination of its effect on actual fingerprint matching or recognition.

In the last decade, biometric identification based on physical and behavioral features has become increasingly popular. Among these features, iris biometric is considered the most trustworthy authentication method. However, there is a lack of user-friendly techniques for iris comparison, and it has not been widely used in forensics applications. Human-in-the-loop systems based on matching and detection of iris crypts have been developed[7], which can capture crypts of different sizes and identify all types of topological changes. Currently, iris recognition is being used in Aadhar card projects.

II. RELATED WORK

The Discrete Cosine Transform (DCT)[2] is a widely used mathematical technique for signal processing and data compression. In the context of fingerprint recognition, the DCT can be used to transform the spatial information of a fingerprint image into frequency domain information. Here is a high-level overview of the DCT algorithm for fingerprint processing:

1. Preprocessing: The fingerprint image is typically preprocessed to enhance its quality and remove noise. This may involve steps such as normalization, binarization, and noise reduction.
2. Divide the Image: The preprocessed fingerprint image is divided into smaller blocks or tiles. Common block sizes for fingerprint processing are typically 8x8 or 16x16 pixels.
3. Apply DCT: In the transformation process, the DCT is utilized to convert pixel values within each block from the spatial domain to the frequency domain. The DCT formula for a block with dimensions N x N can be expressed as follows: F(u, v) = C(u)C(v) * Sum[Sum[f(x, y) * cos((2x + 1)uπ / (2N)) * cos((2y + 1)vπ / (2N))]] for x = 0 to N-1, y = 0 to N-1. Here, F(u, v) represents the transformed coefficient at frequency (u, v), C(u) and C(v) are normalization factors, f(x, y) denotes the pixel value at position (x, y) in the block, and the nested sums encompass calculations performed for each value of x and y within their respective ranges.
4. Quantization: The resulting DCT coefficients represent the frequency components of the fingerprint image. In this step, the coefficients are quantized by dividing them by a quantization matrix. The quantization matrix is typically chosen based on the application requirements and desired compression ratio.
5. Feature Extraction: After quantization, the most significant DCT coefficients are selected to represent the fingerprint features. These coefficients carry the essential information about the fingerprint's ridges and valleys.
6. Compression (Optional): If the purpose is data compression, the quantized DCT coefficients can be further compressed using techniques like entropy coding (e.g., Huffman coding) or transform coding (e.g., JPEG).
7. Matching: The extracted features from the DCT coefficients can be used for fingerprint matching against a database of known fingerprints. Various matching algorithms, such as correlation or minutiae-based matching, can be employed to determine the similarity between fingerprints.

It's important to note that the specific implementation details and parameter choices may vary depending on the fingerprint recognition system and the specific requirements of the application.

Iris recognition typically relies on feature extraction techniques rather than direct application of the Discrete Cosine Transform (DCT). However, if you are interested in understanding how DCT can be used as a part of iris recognition, here is a high-level overview:

a. Image Acquisition: The iris image is captured using an iris imaging system, such as an iris camera or a specialized iris scanner. The image should be of sufficient quality and resolution for accurate feature extraction.

b. Preprocessing: Preprocessing steps are performed to enhance the quality of the iris image and remove any noise or artifacts. This may involve operations such as image normalization, denoising, and segmentation to isolate the iris region.

c. Iris Normalization: The iris region is typically normalized to account for variations in iris size, rotation, and translation. This step aims to transform the iris region into a standard size and shape, making it suitable for subsequent feature extraction.

d. Apply DCT: Once the iris region is normalized, the DCT can be applied to extract frequency domain information. Similar to the fingerprint DCT algorithm, the DCT coefficients are calculated for blocks or tiles within the iris region. The size of the blocks may vary based on the implementation, but commonly used sizes are 8x8 or 16x16 pixels.

e. Quantization and Feature Extraction: The resulting DCT coefficients are quantized to reduce their precision and discard less significant frequency components. The quantization process is typically guided by a quantization matrix specific to iris recognition. The quantized coefficients are then used to extract iris features. Various methods can be employed for feature extraction, such as selecting specific DCT coefficients or computing statistical measures from the coefficients.

f. Matching: The extracted iris features from the DCT coefficients are compared against a database of known iris templates. Matching algorithms, such as Hamming distance or correlation-based methods, can be utilized to determine the similarity between the extracted features and the templates in the database.

III. PROPOSED METHOD

The K-SVD algorithm for fingerprint and iris compression involves sparse coding and dictionary update steps. Here's a step-by-step explanation of the algorithm with mathematical calculations:

1. Step 1:Dictionary Initialization

Let X be a matrix containing signal patches or features. Each column of X represents a signal patch or feature vector.

Initialize an overcomplete dictionary D of size M x K, where M is the dimensionality of the signal patches and K is the desired number of atoms in the dictionary.

Normalize the columns of D to have unit norm.

2. Step 2: Sparse Coding

For each column in X, find a sparse representation[10] using the current dictionary D

a. Let's consider a specific signal patch represented by the column x_i in X

b. Initialize a sparse code vector α_i of size K with all zeros

c. While the sparsity level or representation error is not satisfied:

• Find the best matching atom in D for the residual signal e_i = x_i - D * α_i, where * denotes matrix multiplication.
• Let j be the index of the best matching atom.
• Update the sparse code coefficient α_i(j) with the inner product between the residual and the selected atom:

α_i(j) = (e_i^T * d_j) / (d_j^T * d_j), where d_j is the jth column of D.

• .Update the residual e_i = e_i - α_i(j) * d_j.

d. After convergence, the sparse code α_i represents the sparse representation of the signal patch x_i using the dictionary D.

3. Step 3: Dictionary Update

For each atom in D:

a. Find the set of signal patches[11] that use the atom as a part of their sparse representation.

b. Construct a submatrix X_j containing the columns of X corresponding to those signal patches[14].

c. Perform a least squares regression to find the updated atom d_j that minimizes the representation error:

• Solve min ||X_j - D * α_j||_F^2 subject to ||α_j||_0 <= T, where ||.||_F denotes the Frobenius norm and ||.||_0 denotes the L0 norm (number of nonzero elements).
• The solution to the above problem can be obtained using techniques like least squares, orthogonal matching pursuit (OMP), or basis pursuit.

d. Update the jth column of D with the updated atom d_j.

r. Normalize the updated atom to have unit norm.

4. Step 4:Iterative Refinement

Repeat Steps 2 and 3 for a specified number of iterations or until convergence.

5. Step 5:Compression

After the K-SVD algorithm[13] converges, store the sparse codes α_i and the updated dictionary D as the compressed representation.

Additional compression techniques such as quantization and entropy coding can be applied to further reduce the data size.

6. Step 6:Decompression

To reconstruct the original signal from the compressed representation:

Use the sparse codes α_i and the dictionary D.

Multiply each sparse code α_i with the corresponding dictionary atoms in

D: x_i = D * α_i.

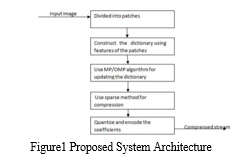
IV. EXPERIMENT

A. Modules

1. Upload Image: This module focuses on the compression of fingerprint images, specifically those with a PNG (Portable Network Graphics) image type. It is worth noting that other image types such as JPEG, GIF, BMP, and others can also be utilized
2. Compress Image using SVD: This module utilizes the K-SVD (K-Singular Value Decomposition) algorithm to compress the uploaded PNG image to its maximum extent, while ensuring that no data loss occurs during compression. Although the module specifically works with PNG images, it is also possible to use other image types such as JPEG, GIF, BMP, etc. After compression, the resulting image is stored as a lossless compressed image.
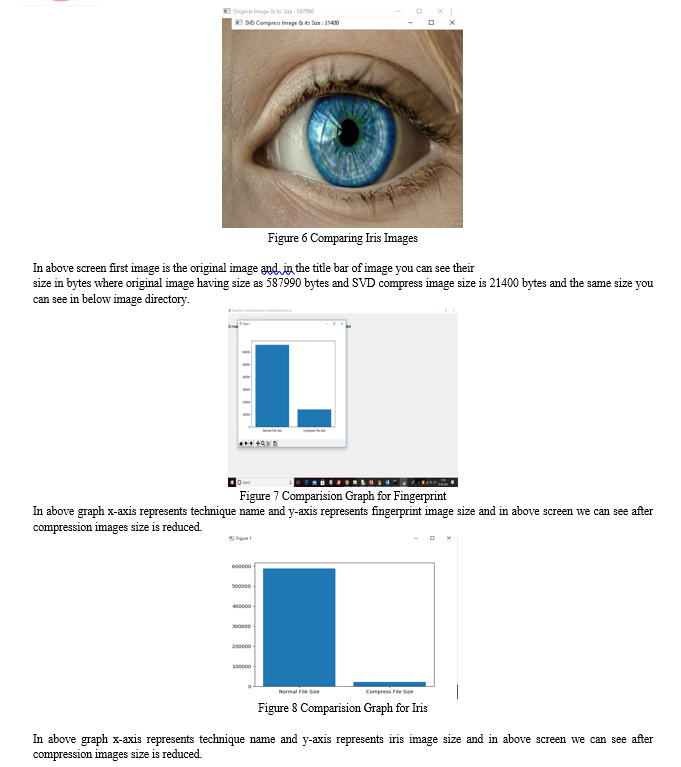
3. Comparison Graph: In this step the size of the original image is compared to the size of the compressed image to evaluate the compression ratio achieved by the proposed method. This comparison is presented using a bar graph, which clearly shows that the compression achieved is at its maximum level.
4. K-SVD Algorithm: The K-SVD algorithm [13] is an iterative approach that proceeds through two alternating steps: sparse coding and dictionary update. During the sparse coding step, the current dictionary is employed to obtain sparse representations for each input example. On the other hand, the dictionary update step involves refining the dictionary to enhance its alignment with the input examples. These two steps are repeated iteratively within the K-SVD algorithm until convergence is achieved.

V. FUTURE ENHANCEMENT

There are several interesting areas that should be explored in future research. Firstly, it would be beneficial to examine the features and techniques used to construct dictionaries. Secondly, the training samples should be expanded to include fingerprints of varying qualities, including those that are "good", "bad", and "ugly". Thirdly, more research is needed to investigate optimization algorithms for solving the sparse representation problem. Fourthly, optimizing the code to reduce the complexity of the proposed method would be valuable. Lastly, it would be worthwhile to explore other potential applications for fingerprint images based on sparse representation.

Conclusion

The paper presents a novel compression algorithm designed specifically for fingerprint and iris images. Despite its simplicity, the algorithm performs well compared to more complex algorithms, particularly at high compression ratios. The minutiae are the key features used in fingerprint and iris recognition, and any compression algorithm used must preserve them to ensure accurate identification. In the case of fingerprint compression, the proposed method using sparse representation and K-SVD dictionary learning showed promising results in preserving the minutiae while achieving high compression ratios.

References

[1] D. Maltoni, D. Miao, A. K. Jain, and S. Prabhakar, Handbook of Fingerprint Recognition, 2nd ed. London, U.K.: Springer-Verlag, 2009. [2] N. Ahmed, T. Natarajan, and K. R. Rao, “Discrete cosine transform,” IEEE Trans. Comput., vol. C-23, no. 1, pp. 90–93, Jan. 1974. [3] C. S. Burrus, R. A. Gopinath, and H. Guo, Introduction to Wavelets and Wavelet Transforms: A Primer. Upper Saddle River, NJ, USA: PrenticeHall, 1998. [4] W. Pennebaker and J. Mitchell, JPEG—Still Image Compression Standard. New York, NY, USA: Van Nostrand Reinhold, 1993. [5] M. W. Marcellin, M. J. Gormish, A. Bilgin, and M. P. Boliek, “An overview of JPEG- 2000,” in Proc. IEEE Data Compress. Conf., Mar. 2000, pp. 523–541. [6] A. Skodras, C. Christopoulos, and T. Ebrahimi, “The JPEG 2000 still image compression standard,” IEEE Signal Process. Mag., vol. 11, no. 5, pp. 36–58, Sep. 2001. [7] Jianxu Chen, Feng Shen, Danny Z. Chen, “Iris Recognition Based on Human-Interpretable Features” in IEEE ISBA,2015. [8] C. M. Brislawn, J. N. Bradley, R. J. Onyshczak, and T. Hopper, “FBI compression standard for digitized fingerprint images,” Proc. SPIE, vol. 2847, pp. 344–355, Aug. 1996. [9] M. Elad and M. Aharon, “Image denoising via sparse and redundant representation over learned dictionaries,” IEEE Trans. Image Process., vol. 15, no. 12, pp. 3736–3745, Dec. 2006. [10] S. Agarwal and D. Roth, “Learning a sparse representation for object detection,” in Proc. Eur. Conf. Comput. Vis., 2002, pp. 113–127. [11] J. Yang, J. Wright, T. Huang, and Y. Ma, “Image super-resolution as sparse representation of raw image patches,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Jun. 2008, pp.1– 8. [12] K. Skretting and K. Engan, “Image compression using learned dictionaries by RLS-DLA and compared with K-SVD,” in Proc. IEEE ICASSP, May 2011, pp. 1517–1520. [13] O. Bryt and M. Elad, “Compression of iris images using the K-SVD algorithm,” J. Vis. Commun. Image Represent., vol. 19, no. 4, pp. 270–282, 2008. [14] Y. Y. Zhou, T. D. Guo, and M. Wu, “Fingerprint image compression algorithm based on matrix optimization,” in Proc. 6th Int. Conf. Digital Content, Multimedia Technol. Appl., 2010, pp. 14–19.

Copyright

Copyright © 2023 Dr. K Kranthi Kumar, K Ninitha, G Sahithi, A. Ruchitha. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.