A Numerical Study on Fluid Flow and Heat Transfer in a Flow Interrupting Ribbed Microchannel under Inlet Flow Pulsation

Abstract

The present work investigates the effect of pulsation on the transport process in a 2D microchannel. The inlet velocity varies sinusoidally in time at a constant dimension less frequency (St=10) and amplitude of 0.8. The working fluid is considered as water which is made to flow in the flow disturbing microchannel whiles the microchannel walls were kept at a uniform temperature. The solution of two-dimensional Navier-Stokes equation was performed using the SIMPLE algorithm with the momentum interpolation technique. The simulations were performed in the laminar regime within the Reynolds number range between 100- 500 for the microchannel. The results of pulsating flow simulations had been analysed and compared with non-pulsating flow simulations. It is observed that the effect of pulsation in flow interrupting ribbed microchannel is significant and more enhancement of heat transfer is observed at higher Reynolds number while keeping the friction factor within tolerable limits.

Introduction

I. INTRODUCTION

Most heat transfer enhancement is based on two main strategies i.e. restarting the thermal boundary layer and using bulk fluid mixing. Devices such as louvers and offset-strip fins restart the thermal boundary layer and may induce vortices to provide mixing. Destruction and restarting of the boundary layer cause an increase in heat transfer by producing a boundary layer that is thinner on average than the uninterrupted boundary layer. Vorticity in the flow can enhance heat transfer through bulk fluid mixing which reduces temperature gradients in the core fluid flow concentrating thermal gradients in the near wall region. It can be established by using the different passive heat transfer technique geometrically as good as by flow pulsation at inlet. There are few works has been reported regarding heat transfer enhancement that can be brought by flow pulsation in the flow interrupted microchannel.

The Reynolds number for flows in microchannels is generally very low as the flow velocity in these small hydraulic diameter passages is quite small. The friction factors and pressure drop are both quite high in microchannels flows since the available surface area for a given flow volume is high as discussed by Kandlikar et al., 2003.

Previous works include the investigations by Cho and Hyun (1990) and Kim et al. (1993). The effect of pulsation in a pipe using laminar boundary layer equations was numerically investigated. They have observed that at the fully established downstream region, the Nusselt number may increase or decrease depending upon the frequency parameter.  The trend is amplified as amplitude increases. Study carried out by Kim et al. (1993) on the thermally developing channel flow with developed inlet profile and isothermal channel walls. The outcome of the study was that the difference in time-averaged heat flux for pulsating and corresponding steady state condition was rather small.

The experimental study conducted by Esmaili et.al (2018) that investigates the effect of designing ribbed microchannel within a Reynolds number range of 184 to 1800. The comparison of flat and ribbed microchannel reveals that heat transfer enhancement is reported in despite of increasing pressure drop. The result also shows that 80% reduction of thermal resistance by implementing of the rib in microchannel.

A numerical study are carried out by Ghale et al. (2015) to investigate the effect of turbulators on fluid flow and heat transfer in a ribbed microchannel. It is found that the Nusselt number and Friction Coefficient of Nanofluids in the ribbed microchannel are higher than those of simple microchannel and enhancement is more with the width of the ribs.

The laminar forced convection heat transfer of water–Al2O3 nanofluids through a horizontal rib-microchannel was studied numerically by Akbari et al. (2106) at very low Reynolds number.

The result shows that there is a sharp augmentation in friction coefficient, heat transfer rate and Nusselt number. It is also found that changing the solid volume fraction and the rib's height, cause significant changes in temperature and dimensionless velocity along the canter line of the flow, through the ribbed areas.

Di Qi (2022) studied numerically the effect of rib diameter on flow boiling heat transfer with staggered rib arrays in a heat sink. The analysis shows that heat transfer rate increases and wall temperature decreases with the increase of rib diameter. Further it is observed that heat transfer performance is best at larger rib diameter.

There are many numerical models discussed assuming unsteady flow by adopting different passive enhancement technique in a microchannel.  Also, very less paper studied numerically, this unsteady single phase fluid flow in flow interrupting ribbed microchannels and accordingly there is a need for systematic assessment of the impact of flow pulsation in heat transfer from ribbed microchannel at constant wall temperature.

The purpose of this work is to investigate numerically by comparing the fluid flow and heat transfer process in a flow interrupting ribbed microchannel with pulsating flow at inlet. This study will be restricted on the thermal analysis of single-phase flow on 2D only. Furthermore, other assumption and limitations inherent to the current model are (1) the flow is limited in the Reynolds number regime of 100? Re ?500 which is expected in most microfluidic systems, (2) the hydraulic diameter of a microchannel is taken here more than 67µm, so continuum model is considered in this case. The flow at the inlet of the domain is considered in a sinusoidal pattern with constant frequency and amplitude. The present study focuses with frequency at St=10 and amplitude at A=0.8. The simulations are focused to find out the zone of the maximum heat transfer and the behaviour of the unsteadiness affecting the heat transfer mechanism.

II. PROBLEM FORMULATION

A. Model

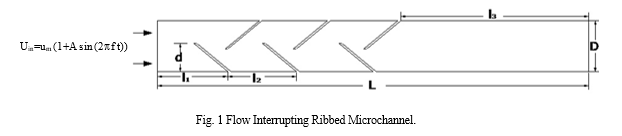
The model of flow interrupting microchannel is shown in Fig 1 where the length and diameter of the micro microchannel is denoted by L and D. The length of microchannel is assumed to be very long compared to the diameter. Hence the problem can be considered to be two dimensional. From entry to first obstruction (l1) length is 50mm and the distance between two obstructions (l2) is 50mm.  The obstruction free length (l3) of the channel is 125mm. The total length (L) of the channel is 300mm and diameter (D) is 10mm. The depth (d) up to which the obstruction exists is 6 mm.

A structured mesh was developed for the solution domain by using the mesh generation facility. The numerical simulation was performed by solving the time dependent, continuity momentum and energy equations for a compressible fluid as shown below:

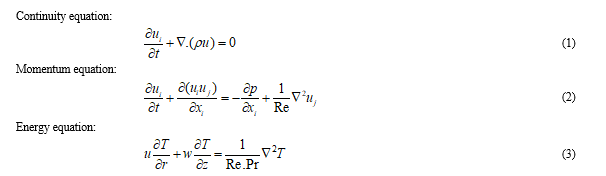
C. Solution Procedure

The governing equations were solved using the SIMPLE algorithm, a finite volume formulation of Patankar, 1980. The iterative SIMPLE calculation process begins by guessing the pressure field. During the iterative process, the discretized momentum equations are solved using the guessed pressure field. Applying the finite-volume method, the equations for the x-momentum and y-momentum that yield the velocity components, u and v. These guessed fields are progressively improved through the iteration process until convergence is achieved for the velocity and pressure fields. This scheme does not change the formal second order accuracy of the basic discretization process. In each time step, calculations were carried and till the residuals reached a value below 10-6 for continuity and momentum equation and 10-8 for energy equation. The governing equations were solved by strongly implicit procedure of Stone (1968). Under relaxation factors below 1.0 were used for obtaining convergence.

A structured mesh was developed for the solution domain by using the mesh generation facility was preferred as 300 x 75 for all cases after performing a rigorous grid independence check. The length of the computational domain was assorted for five different levels of Re, as the growing length is a function of Re. Again, different grid distributions were needed for different Re, depending upon the L/D ratio. Typically (300 X 75) and (300 x 50) grids were used for Re = 100, 200, 300, 400 and 500 for this interrupted ribbed microchannel. Grid independence was made certain by computing as a minimum at three dissimilar grid levels. The bulk Nusselt number at Re value of 100 for non-ribbed straight microchannel were compared with available literature Cebeci et al. (1984) and found to agree within 3%.

III. RESULTS AND DISCUSSION

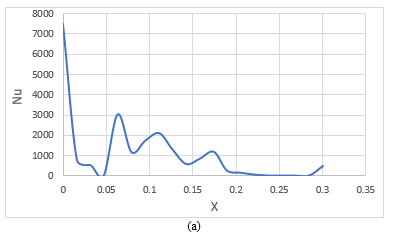
The numerical model was tested within the range of 100≤ Re ≤ 500. The Nusselt number is a characteristic of the heat transfer whether the heat transfer is based on convection or conduction. With a Nusselt number of 1 the conduction and convection are of similar magnitudes, while a large Nusselt number corresponds to a more active convection. It is observed from Fig 2 that at Reynolds number near to 100 the Nu value for pulsating cases is almost close to the steady case. This is because at low Re the recirculation near the obstruction is observed less even at pulsating flow condition and the flow seems to be dominated by viscous forces.

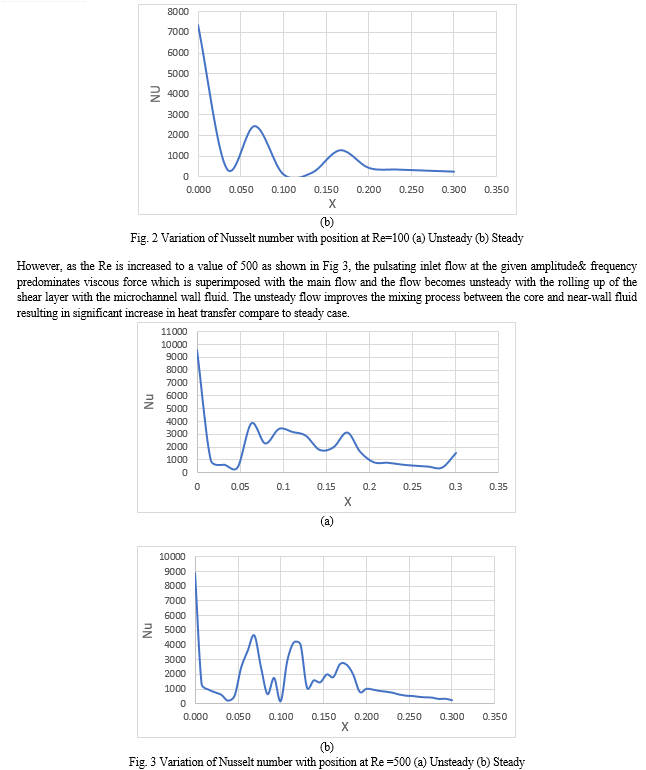
The pulsation effect is calculated by the enhancement ratio which is the ratio of time averaged Nu value for unsteady case to the local Nu value calculated for the case without pulsation. We define the enhancement ratio is h = Nuavg/Nus, where Nuavg is time averaged value of local Nussle number at some location and the Nus denotes the case when the inlet profile is steady for the same location. Thus, a value of h over 1.0 indicates enhanced heat transfer at the location.

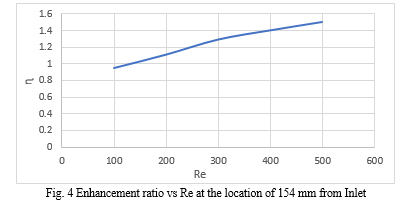
From the Fig 4, it is observed that the heat transfer enhancement ratio at lower range of Re is less comparing it with higher range of Re. This is because pulsating flow is superimposed with the mean flow of the ribbed microchannel making the flow unsteady enough causing a good mixing at higher value of Re otherwise it would have been behaving very low instability resulting in poor heat transfer rate. As Re is increasing, a gradual increase of enhancement ratio is observed because of more unsteadiness of the mean flow.

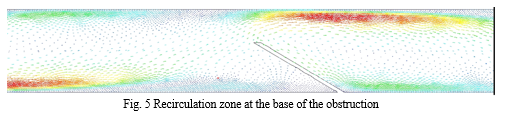
This analysis concentrates on the comparative study of fluid flow in a microchannel with pulsation and without pulsation. In case of simple microchannel for steady laminar case, the boundary layer grows up rapidly and boundary layer thickness increases due to viscous shear stress is acting in the fluid. The viscous shear force predominates in the fluid flow results in higher friction at low Reynolds number. Here it is noticed from the Fig 5 that at the base of rear side of the rib which are at 45? with base of the microchannel, the recirculation zone are created which experiences deaccelerating flow and an adverse pressure gradient. This artificial vortex makes the large pressure drop immediately at the rear side of the rib.

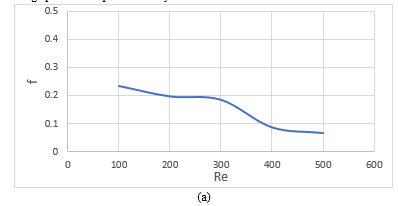
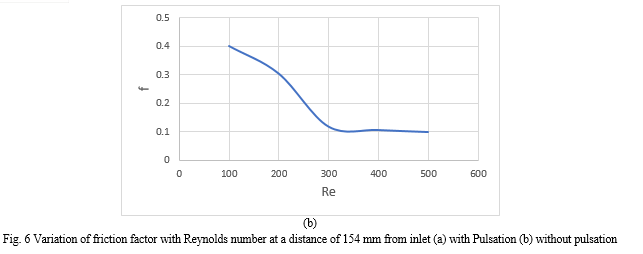
The friction factors versus Reynolds number at constant amplitude and frequency are shown in Fig 6. It can be seen from figure that in the low Reynolds number region friction is more. This is the flow region where the flow is viscous in nature causing high pressure drop results in increase friction factor. The pressure drop is mainly caused by the surface friction effect. In the high Reynolds number region, with further increase of Reynolds number the friction factor decreases, that is the flow resistance decreases with higher flow velocity and low pressure drop.

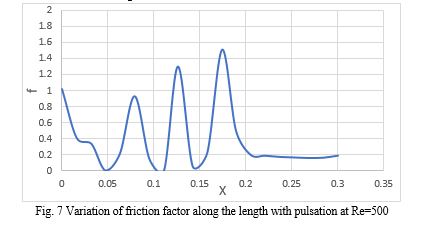
The higher friction factor is observed at a particular Reynolds number due to the higher pressure drop at the entry where the flow is hydrodynamically and thermally developing and after that flow becomes fully developed along the length. Fig 7 shows the variation of friction factor along the longitudinal axis which reveals that there is periodic change of friction factor from higher value to lower value at particular Reynolds number within the range. Obviously, it is found that the obstructed region of the microchannel forms convergent and divergent area.  In the convergent region the cross-section area decreases that cause the more resistance to flow of fluid due to the more viscous shear stress and it contributes the increase of friction coefficient at the narrow spaces. In the divergent area, contrary to the convergent area, the cross-section area increases and the fluid is experienced less resistance to flow, causes rapid decrease of friction coefficient at the divergent section. 

???????

Conclusion

In this section, comparative study of fluid flow and heat transfer in a microchannel with pulsation and without pulsation was conducted. The numerical analysis reveals that inlet flow pulsation enhances the heat transfer significantly at high Reynolds number whereas at low Reynolds number a small amount of enhancement is noticed at a constant amplitude and frequency for both the cases. The non-dimensional pressure drop is reported less for unsteady flow due to flow pulsation compare to the case of steady flow. The friction factor for unsteady flow is also noticed less than the steady. The overall analysis of flow interrupting ribbed microchannels reveals better thermal performance with inlet flow pulsation than non-pulsating case. A. Nomenclature A Amplitude Nu Time-averaged Nusselt number (hx/?) P Pressure Q Total heat transfer rate Re Reynolds number (uavR/?) St Strouhal number (fDh/um) t Time u,v Velocity components in axial direction

References

[1] S.G. Kandlikar, S. Joshi, and S. Tian, “Effect of surface roughness on heat transfer and fluid flow characteristics at low Reynolds numbers in small diameter tubes”, Heat Transfer Engineering. 24, pp. 4-16, 2003. [2] H. W. Cho and H.W. Hyun, “Numerical solutions of pulsating flow and heat transfer characteristics in a pipe”, Int. J. Heat Fluid Flow, vol. 11, pp. 321-330, 1990. [3] T. Cebeci and P. Bradshaw, “Physical and computational aspects of convective heat transfer”, Springer New York. 1984. [4] S. V. Patankar, Numerical Heat Transfer and Fluid Flow. McGraw-Hill, New York, 1980. [5] Q. Esmili, A. A. Ranjbar, and S. Porkhial, “Experimental analysis of heat transfer in ribbed microchannel”, Int. J. Thermal Science, vol. 130, pp. 140-147, 2018. [6] Z. Yari Ghale, M. Haghshenasfard, and M. Nasr Esfahany, Investigation of nanofluids heat transferin a ribbed microchannel heat sink using single-phase and multiphase CFD models, Int. Communications in Heat and Mass Transfer, vol. 68, pp. 122-129, 2015. [7] C. M. Rhie and W. L. Chow, “Numerical Study of the Turbulent Flow Past an Airfoil with Trailing Edge Separation”, AIAA Journal, vol. 21, pp. 1525-1532, 1983. [8] O. A. Akbar, D. Toghraie, A. Karimpour, R. M. Safai, and M. Dahari, “Investigation of rib’s height effect on heat transfer and flow parameters of laminar water–Al2O3 nanofluid in a rib-microchannel”, Applied Mathematics and computation, vol. 290, pp. 135-153, 2016. [9] Di Qi, He Jing, Y. Xu, and Q. Wang, “Effect of rib diameter on flow boiling heat transfer with staggered rib arrays in a heat sink”, Energy, vol. 239, Part D, 122323, 2022. [10] H. L. Stone, “Iterative solution of implicit approximations of multidimensional partial differential equations”, SIAM Journal of Numerical Analysis, vol. 5(3), pp. 530-538, 1968. [11] C. M. Rhie and W. L. Chow, “Numerical Study of the Turbulent Flow past an Airfoil with Trailing Edge Separation”, AIAA J., vol. 21, pp. 1525-1532, 1983.

Copyright

Copyright © 2022 Tapas Kumar Nandi, Santanu Duari. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.