Handwritten Mathematical Expression Solver using CNN

Abstract

Mathematics is the universal language. It is the core of all the scientific discoveries and is used extensively in all possible fields. Hence, there arises the need for fast computation and instant results. This has led to the development of various technologies and machines which would ease the strain on humans and also reduce the error and delays caused by them. Our project caters to these needs by reducing the effort on user side. We want to make the experience of experimenting with equations as simple as possible. The application is capable of performing fast calculations on human handwritten mathematical expressions. Basic calculations like arithmetic and trigonometric functions can be done along with simultaneous equations. The expression is extracted from the image and each character, symbol and number is recognised and then the entire expression is further being solved displaying all possible solutions. The application developed is simple and user-friendly tool that can leverage the power of existing powerful math packages.

Introduction

I. INTRODUCTION

Discovery, that is the word we associate with finding something new. The reason for this is that this universe already has everything it requires, it's just in a form that mankind has yet to comprehend or discover. Mathematics is the simplest way to understand the universe's transformations and intricacies. The language of mathematics which can describe the nature of the universe to the shapes and structure and pattern of almost all objects that we perceive through our senses. Take any aspect and you will find a mathematical description for it. For years mankind has tried to decipher this mathematical code by numerous methods and formulae which were worked upon for years and years. And today we have reduced the time gap to get answers for tedious methods and procedures with the help of new technologies and gadgets. The most general example would be a calculator which is used instead of manually working out mathematical methods thus reducing the percentage of human error associated with it. But using the calculator to solve the humongous equations and find answers for them is a tedious task since it requires the equations to be entered accurately. Therefore, another need for innovation came to life and thus technology which could scan documents and interpret what is written and further find the answer for it to ease the daily humdrum. This is where machine learning and neural networks come into the picture, where a model is built in such a way that it can think and solve the problems in the same way a human brain would do but swiftly and efficiently. Mathematical equations form an integral part of most research work, so researchers use such mathematical tools to save time and boost efficiency keeping in mind the complexities and syntax of the chosen tool. If the syntax rules are not followed properly, one might not get the desired output. Another concern is the task of entering all the equations and expressions properly leaving no gap for human error since the system will be performing the calculations based on the input given. This requires a lot of time and human intervention and also good knowledge of the tool being used. A convenient solution to this can be to build a user-friendly tool that would capture the image of a mathematical equation, recognise the equation embedded in it and present the user with the required solution. This is precisely the tool we have developed and discussed throughout this paper. Computers can be made to think and act like a human would, by forming a neural network and also retaining their computational superiority. In our project, we have attempted to simplify the interaction between humans and computers pertaining to the processing and solving mathematical equations. We have focused on building a model which is simple to understand, by not restricting the user with various syntax rules and complexities.  In today’s world there are many tools, simulators which are available for mathematical purposes. However, more the features, more the awareness about the particular tool is required from the user. To shorten this gap of excessive awareness on the user’s side, the machine could be trained to understand the user’s needs more accurately with very less effort from the concerned user. This being the ideology we have tried to build a machine learning model which will take the image input of the mathematical expression written by the user and identify the input expression and provide the answer with accuracy achieved while building the model.

II. LITERATURE SURVEY

The Internet is the key to connecting with the world and helping us learn. It is one of the greatest pillars to educate many in some way or the other. But, in the field of mathematics, considering the use of Greek letters and special symbols in mathematical equations, it is difficult to give these as an input to the internet. This issue has been addressed as we have Latex to represent these equations, however using Latex requires some training and intensive practice. On the other-hand, some development is done in recognition of these expressions using machine learning. Mathematical expression recognition typically consists of two major stages: symbol recognition and structural analysis. Both symbol recognition and structure analysis of two-dimensional patterns have been extensively studied for decades. The recognition of characters requires segmentation. Segmentation has been studied by many and includes various approaches like use of modular systems [3], X-Y cutting [4], recursive X-Y cut[5]. Symbol recognition also uses some approaches like template matching [4][6][7], structural approaches by Haton[8] and Chan and Yeung[9] and statistical approaches by Chen and Yin [10], Fateman and Tokuyasu [11], Ha [12] using neural networks. Offline and online are the two ways by which mathematical expression recognition can be done. Here we have used the offline way in which the user input is a complete expression of the problem to be solved. Offline recognition has been attempted by building relation trees [2][4], expression trees built through top-down and bottom-up approaches [5], use of nearest neighbours [15][16], application of convex hull [17].

Recent works done in the field includes the works of Zanibbi [18] which recognizes the math expressions online, sketched on the computer. Then an Offline Handwritten Mathematical Recognition [19] which also uses CNN and gives detail information on segmenting the expressions effectively to detect the horizontal link, upper link, superscript link, sub-expression, subscript link and lower link. The recognition accuracy of neural network-based handwritten recognition systems can be improved by changing the features considered in the classification and segmentation stages. Edge detection was used in the segmentation stage, followed by morphological operations, and special features such as skew, standard deviation, mean, variance, and so on were used instead of common features such as thickness, thinness, and area [20].

III. PROPOSED MODEL

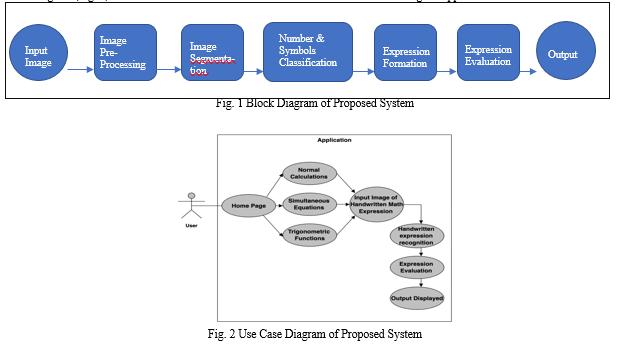
The proposed model consists of two phases mainly, first the handwritten expression recognition and second is expression evaluation phase. The input image provided by the user is pre-processed and segmented to recognize and predict each individual character, number and symbols [1]. After recognition the mathematical expression is formed which is further processed using python libraries to provide the calculations.  The Block Diagram (Fig. 1) represents the procedure in which entire processing is carried out. The Use Case Diagram (Fig. 2) shows all the use case scenarios that a user encounters while using the application.

IV. IMPLEMENTATION

The model created is a sequential model. The project implementation is divided into two phases, Handwritten Expression Recognition Phase and Expression Evaluation Phase.

A. Dataset

The dataset was used from Kaggle and it consisted images of handwritten digits from 0 to 9 along with various math symbols and alphabets. It consists of symbols from the Greek alphabet, English alphanumeric characters, math and set operators, basic predefined math functions (such as sin, cos etc.) and math symbols (such as sum, sqrt, delta etc.). Every specific element has more than 100 images for the model to train on and predict. Dataset is fairly diverse since it contains handwritten samples of different individuals which helps the CNN model to train on various parameters. Samples without any variation won’t be helpful since they usually lead to overfitting. In this project we have used limited number of symbols and alphabets rather than considering all the 26 alphabets for computation purposes. The dataset could be expanded even further to perform even more complex calculations.

B. Pre-processing

1. Binarization:  The conversion of an input image into a bi-level target image is binarization. The term bi indicates two which means that image pixels are divided into two groups, black and white pixels. The primary goal of image binarization is to sort an image into foreground and background text. The given input image may consist of noise or other unwanted information which can affect the processing of the expression. Hence, the conversion of the input image into binarized image is necessary.

2. Contour based Segmentation: Contours are defined as the line connecting all the points along an image's borders that have the same intensity. Contours are useful for shape analysis, determining the size of an object of interest, and object detection. The findContours() function in OpenCV aids in the extraction of contours from images. It is most effective with binary images. These contours segregate the handwritten characters, symbols and numbers based on their intensities in binarized image which are than further used for recognition.

C. Building Model

The model is built using Keras. Necessary modules and layers from keras are imported which would form the model. The to-categorial function is imported for forming the different classes for the classification of symbols and numbers. As many varieties of symbols, characters and numbers are involved, many classes are formed. The model created is a Sequential model. The Convolution and MaxPooling layer are applied one after another. The input layer is encompassed in the Convolution layer. This layer applies the convolution operation to the input layer and then passes the result to the next layer. The work of this layer is to change all the pixels in its responsive field into a single value. By this a vector is obtained which is given to the MaxPooling layer.

The MaxPooling layer is used to reduce the dimensionality of the vector by replacing each cell in the array with the max value of the sub matrix part of the required size around the cell in consideration. Dropout layer is included to avoid overfitting of the model. It randomly sets the outgoing edges of neurons that make up hidden layers to 0 at each update. While the data is passing and switching from one format to another, the weight ordering may change. This may affect the output and hence the Flatten layer is used. It adds an extra channel to the batch size. It doesn’t much affect the output but is used as a form of prevention. The Dense layer is the main part of the model where the neural networks are formed and which result in the correct prediction. Three layers of Dense are applied to the model for better accuracy with activation=’ReLU’. The model works like a brain to analyse and classify from the data given in training and based on that, predict into which class the given component can be classified.

The architecture used for our CNN model is described as follows:

Layer 1: Convolutional Layer

• Input Shape = (28, 28, 1)

• Filter size = (5, 5)

• ReLU activation function

Layer 2: Pooling Layer

• MaxPooling

• Pool size = (2, 2)

Layer 3: Convolutional Layer

• Filter size = (3, 3)

• ReLU activation function

Layer 4: Pooling Layer

• MaxPooling

• Pool size = (2, 2)

Layer 5: Dropout Layer

• Drop probability = 0.2

Layer 6: Flatten Layer

Layer 7: Fully Connected Layer

• 206 output neurons

• ReLU activation function

Layer 8: Fully Connected Layer

• 128 output neurons

• ReLU activation function

Layer 9: Fully Connected Layer

• 50 output neurons

• ReLU activation function

Layer 10: Fully Connected Layer

• 22 output neurons

• Softmax Activation function

D. Expression Evaluation

After the recognition of the characters and symbols, the expression is passed to the function to solve and display the solution. For all the mathematical processing python library called SymPy is used [21]. SymPy depends on mpath which is a python library for real and complex floating-point arithmetic with arbitrary precision. The final answer after calculation is displayed on the GUI based page.

VI. ACKNOWLEDGMENT

The authors would like to express their gratitude to Kaggle for making the handwritten math symbols’ dataset available for public use. We also sincerely thank the skilful developers of Keras, Tensorflow and Python for their ceaseless efforts in maintaining the libraries.

Conclusion

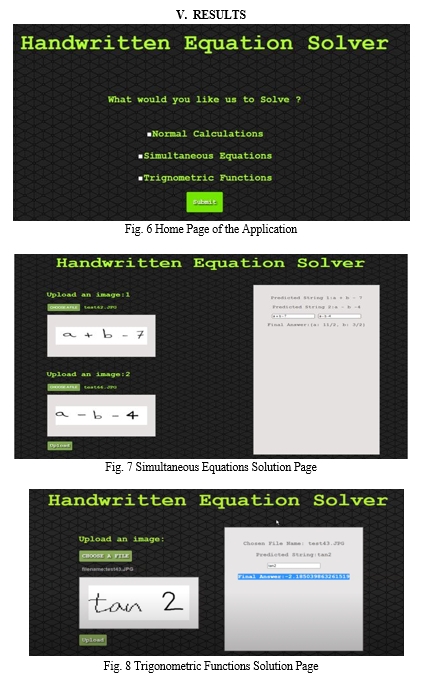
This project focuses on developing a machine learning approach to solve math problems along with character and symbol recognition. The motivation was to create a user friendly application which will be simple and easy to use, without feeling the need to study the usage of the tool or complex syntaxes. It reduces the task on user side as direct images can be given to the application and then get the equivalent solution for it. The discussed web application can solve all the basic arithmetic calculations, trigonometric calculations and simultaneous equations in two variables. With more rigorous training and extension of dataset the capability and accuracy of the model in general can be increased. It can further be extended to solve more complex calculations like differential equations and integrations. Also, the product tool can be made more efficient where it would recognize and solve equations written in groups and reduce the task from the user’s side to input individual equation images.

References

[1] Xue-Dong Tian, Hai-Yan Li, Xin-Fu Li, & Li-Ping Zhang. (n.d.). Research on Symbol Recognition for Mathematical Expressions. First International Conference on Innovative Computing, Information and Control - Volume I (ICICIC’06). doi:10.1109/icicic.2006.506 [2] Okamoto M. Recognition of mathematical expressions by using the layout structure of symbols. InProc. 1st Int. Conf. Document Analysis and Recognition, 1991 1991 (pp. 242-250). [3] Faure and Z. Wang, “Automatic perception of the structure of handwritten mathematical expressions,” Computer Processing of Handwriting, pp. 337 –361, 1990Faure C, Wang ZX. Automatic perception of the structure of handwritten mathematical expressions. In- Computer processing of handwriting 1990 (pp. 337-361). [4] M. Okamoto and A. Miyazawa. An experimental implementation of a document recognition system for papers containing mathematical expressions. In H. S. Baird, H. Bunke, and K. Yamamoto, editors, Structured Document Image Analysis, pages 3653. Springer- Verlag,Berlin, 1992. [5] Ha J, Haralick RM, Phillips IT. Understanding mathematical expressions from document images. InProceedings of 3rd International Conference on Document Analysis and Recognition 1995 Aug 14 (Vol. 2, pp. 956-959). IEEE. [6] Chou PA. Recognition of equations using a two-dimensional stochastic context-free gram- mar. InVisual Communications and Image Processing IV 1989 Nov 1 (Vol. 1199, pp. 852- 865). International Society for Optics and Photonics. [7] Yasutomo Nakayama. 1989. Mathematical formula editor for CAI. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (CHI ’89). Association for Computing Machinery, New York, NY, USA, 387–392. DOI:https://doi.org/10.1145/67449.67523 [8] A. Belaid and J. -P. Haton, ”A Syntactic Approach for Handwritten Mathematical Formula Recognition,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-6, no. 1, pp. 105-111, Jan. 1984, doi: 10.1109/TPAMI.1984.4767483. [9] Chan KF, Yeung DY. Recognizing on-line handwritten alphanumeric characters through flexible structural matching. Pattern recognition. 1999 Jul 1;32(7):1099-114. [10] L. H. Chen and P. Y. Yin. A system for on-line recognition of handwritten mathematical expressions. Computer Processing of Chinese and Oriental Languages, 6(1):1939, June 1992. [11] Fateman RJ, Tokuyasu T, Berman BP, Mitchell N. Optical character recognition and parsing of typeset mathematics1. Journal of Visual Communication and Image Representation. 1996 Mar 1;7(1):2-15. [12] Ha J, Haralick RM, Phillips IT. Understanding mathematical expressions from document images. InProceedings of 3rd International Conference on Document Analysis and Recognition 1995 Aug 14 (Vol. 2, pp. 956-959). IEEE. [13] Faure C, Wang ZX. Automatic perception of the structure of handwritten mathematical expressions. In Computer processing of handwriting 1990 (pp. 337-361). [14] Pfeiffer JJ. Parsing graphs representing two dimensional figures. InProceedings IEEE Workshop on Visual Languages 1992 Sep 15 (pp. 200-206). IEEE. [15] Lee HJ, Wang JS. Design of a mathematical expression recognition system. InProceedings of 3rd International Conference on Document analysis and Recognition 1995 Aug 14 (Vol. 2, pp. 1084-1087). IEEE [16] Chan KF, Yeung DY. Mathematical expression recognition: a survey. International Journal on Document Analysis and Recognition. 2000 Aug 1;3(1):3-15. [17] Miller EG, Viola PA. Ambiguity and constraint in mathematical expression recognition. InAAAI/IAAI 1998 Jul 1 (pp. 784-791). [18] Zanibbi R, Blostein D. Recognition and retrieval of mathematical expressions. International Journal on Document Analysis and Recognition (IJDAR). 2012 Dec 1;15(4):331-57. [19] L. D’souza and M. Mascarenhas, ”Offline Handwritten Mathematical Expression Recognition using Convolutional Neural Network,” 2018 International Conference on Information , Communication, Engineering and Technology (ICICET), 2018, pp. 1-3, doi: 10.1109/ICI- CET.2018.8533789. [20] Sagar Shinde, Dr. R. B. Waghulade, Dr. D. S. Bormane,“A new neural network based algorithm for identifying handwritten mathematical equations ”, International Conference on Trends in Electronics and Informatics, 2017. [21] SymPy Python Library https://www.sympy.org/en/index.html

Copyright

Copyright © 2022 Abhiruchi Patil, Teena Varma. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.