Heat Transfer Analysis of Micro Polar Fluid with AL2O3 and CuO Hybrid Nanofluid Over a Plate with and Without Out Viscous Dissipation

Abstract

This work analysis investigated with the boundary layer stream and heat transfer aspects of a micropolar nanofluid over a porous shrinking sheet with thermal radiation. The boundary layer equations governed by the partial differential equations are transformed in to a set of ordinary differential equations with the help of suitable local similarity transformations. The coupled nonlinear ordinary differential equations are solved by the commercial MATLAB code bvp4c.The solutions of dimensionless velocity ,velocity gradient and temperature profiles are analyzed by the effect of various controlling flow parameters nonlinear parameter ,material property and Eckert number. and temperature and Prandtl number. Physical quantities such as skin frication coefficient, local heat, computed.

Introduction

I.  INTRODUCTION

The technical and scientific advances have bring a great development of attention in constructing dissimilar types of fluids and investigate their flow performance in a variety of practical geometries. Fluids with microstructures act in a different way as of the conventional fluids. The flow and heat transfer performance of these fluids cannot be described adequately with the classical theory of Newtonian fluid flows. Several theories have been existing to describe the very nature of these fluids. However, theory of micropolar fluids accessible by Eringen [1] provides ample details necessary for justification of dynamics of such fluids. Micropolar fluids consist of rigid, arbitrarily leaning, sphere-shaped particles with their possess spins and micro rotation, hovering in a viscous medium. At this point the microelements are permissible to experience unbending rotation only devoid of extend. The micropolar fluid representation, at a distance as of us speed vector involve a micro rotation vector and a twist limit to replicate the kinematics of micro rotation. These fluids have mono symmetric stress tensor. Eringen [2] extensive his assumption for thermo-micropolar fluids and resulting the constitutive laws. Ariman et al. [3,4] presented an outstanding appraisal of micropolar fluids and their applications. Ahmadi [5] investigated the boundary layer flow of micropolar fluids past a semi-infinite plate. The fundamental hypothesis of micropolar fluids can be viewed in the book printed by Eringen [6] as well as by Be’g et al. [7]. Rehman et al. [8] considered heat transfer in two-dimensional steady hydro magnetic natural convection flow of a micropolar fluid past a non-linear stretching sheet with temperature dependent viscosity presence of transverse magnetic field near a stagnation point. Berre et al. [9] described detailed reviews on modeling approaches for flow in fractured porous media, from physical, conceptual and mathematical Upendar and Srinivasacharya [9] analyzed a mathematical model for the steady, mixed convection heat and mass transfer along a semi-infinite vertical plate embedded in a micropolar fluid in the presence of a first-order chemical reaction and radiation. Sharma et al. [11] studied the fully developed electrically conducting micropolar fluid flow and heat transfer along a semi-infinite vertical porous moving plate including the effect of viscous heating and in the presence of a magnetic field applied transversely to the direction of the flow. Mohammedein and Gorla [12] analyzed the flow of micropolar fluids bounded by a stretching sheet with a prescribed wall heat flux, viscous dissipation and internal heat generation. Abo-Eldahab and El-Aziz [13] considered heat transfer effect in a micropolar fluid flow induced by a stretching surface immersed in a porous medium with uniform free stream. Ahmad et al. [14] obtained closed form solution for a viscous, incompressible, MHD flow over a porous stretching sheet. Dayyan et al. [15] studied the Newtonian fluid flow with heat transfer through porous medium and presented analytical solution by employing the Homotopy Analysis Method (HAM). Aluminum Oxides that are known as chemical combination (Al2O3) or Alumina can be counted for a part of Nanoscale elements that is applied in order to make rigorous thermal quality performance of Molecular liquids. They have been classified into two types that are known as αAl2O3 or γAl2O3 based on their magnitudes.

Phenomenon of bunch scattering on the stretching cylinder through Al2O3 and Cu–water-Nanofluids has been studied by Alshomri and Gui [16]. The entropy generation and 2D stream property in γAl2O3−H2O and γAl2O3−C2H6O2 Nanoliquids by Prandtl number model has been investigated in [17].3D flow state in γAl2O3−H2O and γAl2O3−C2H6O2 Nanoliquids amid parallel rotating surfaces has been interrogated by Khan et al [18]. Also, this type of Nanoliquids from aspect of entropy analysis of model has been worked by Hayat et al [19].Chemical reaction and Thermal radiation of MHD streaming of Nano liquids and heat transport investigation on Water based Nanofluids coated with Ag, TiO2, Cu and Al2O3 on a stretchable sheet has been surveyed by Jain et al [20]. The effect of viscous dissipation effects with different parameters are analyses by Kartini Ahmad, ea. al [16] . The present aim of the paper is to analyses the numerical simulation of water, water based nano fluid and water base hybrid nanofluid. The present problem considered with  micro polar fluid passing over a sheet eith effect of viscous dissipation effect. The fluid is passing over a the sketching plate at different temperatures 400C ,600C. to get the variation beteen the Pd .the other parameters  n , Ec [viscous dissipations parameters. The effect various parameters with nondimensional temperature and velocity profiles are Nusselt numbers, Skin friction are graphically.  

II.  MATHEMATICAL MODELING

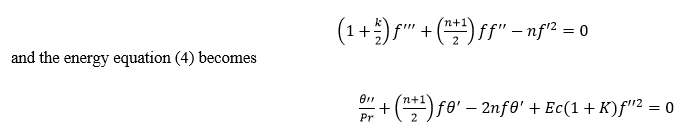
III. PROPERTIES OF NANOFLUID AND HYBRID NANOFLUID

The properties of nanofluid and hybrid nanofluid are evaluated from the literature with the following equations in table 1. and 2.0

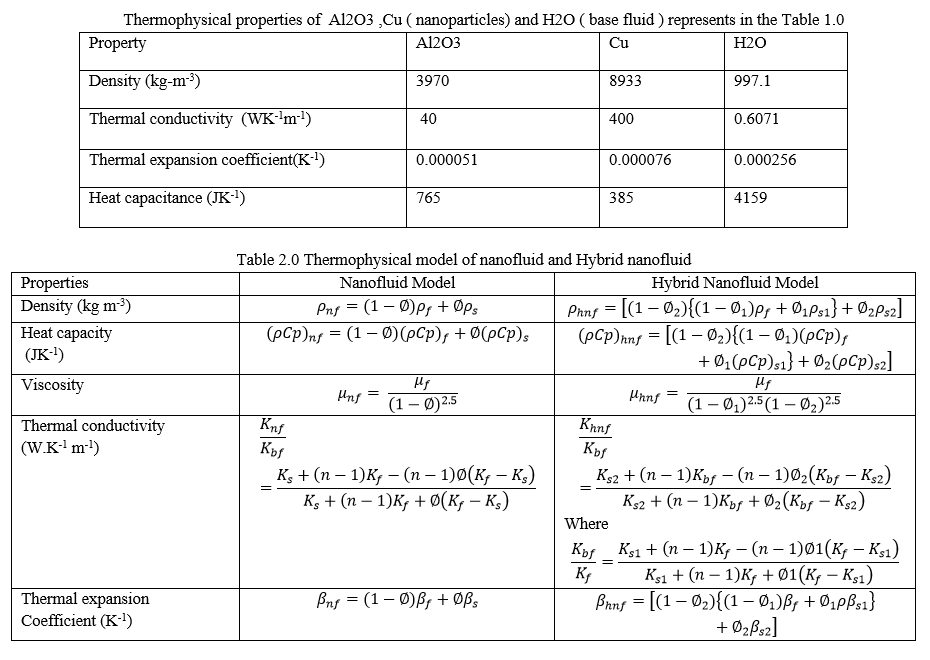
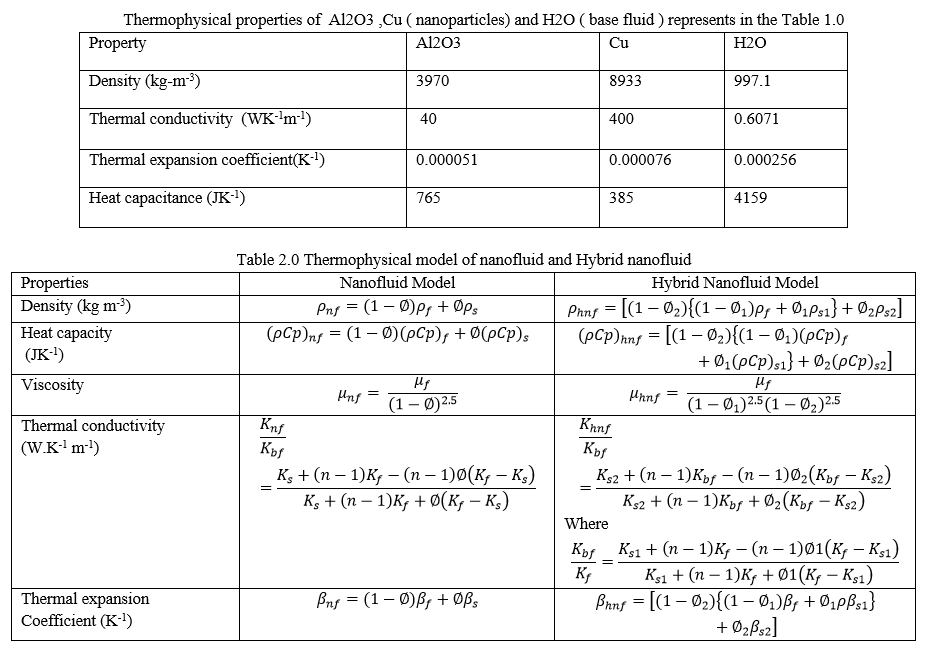
IV. NUMERICAL METHOD

The similarity solutions are adopted for the present problem .The equations[8] ,[9] with boundary conditions [10],[11],12], [13] and [14] solved obtained from the transformation are solved with a finite difference method and compared with MATLAB bvp4c code. The skin friction and Nusselt number are calculated with the equations [13] &[14] .  The transformed boundary layer equations are converted into first order differential equations and solved with the given boundary conditions.

V. RESULTS AND DISCUSSIONS

The fig1.0 represents the variation of velocity profiles for without micro rotation and viscous dissipation and nonlinear parameter.  [K=0,Ec=0,n=0] the fluid itself acts as ordinary nanofluid. The effect of prandtl number on velocity profile are notified. The different Prandtl numbers at different Temperatures are considered. The present problem analysis the water, and

Water base   nanofluid and combined Al2O3 and CuO hybrid nanofluids are considered. Prandtl numbers for 400C and 600C

water and water based nano and hybrid nanofluids are used and analyzed for the current problem From the figure 1.0 & 2.0  the effect of Prandtl number has less significance on velocity profiles

 The figure 3.0 represents the effect of Pr on non dimensional temperature . the temperature profiles are increases with increasing the temperature and the Pr values. The temperature profiles for the hybrid nanofluid as higher than water and nanofluid Al2O3, Cuo due to its moderate properties .

The figure 4.0 and figure 5.0 represents the variation of local Nusselt number and skin friction factor. The local Nusselt numbers are increases with increasing the temperature and Pr from the figure 6.0  there no

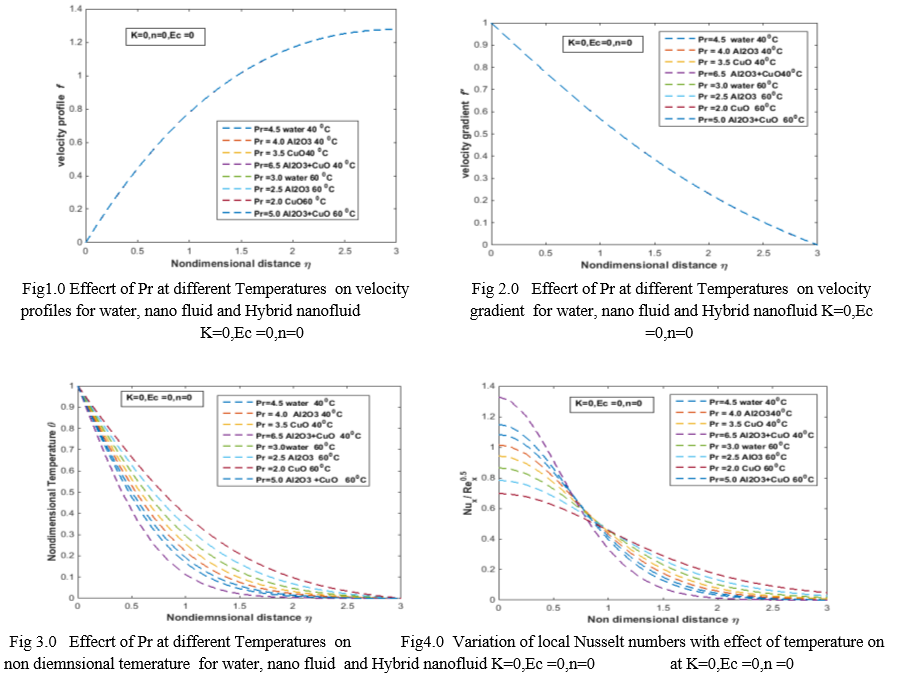
Much significance on skin friction of Pr at different Temperature. Figure 6.0 and Figure 7.0 represents    effect of nonlinear parameter n .the computations are innovated for different values of nonlinear parameter [n=0,1,2]   on velocity profile and velocity gradient  at the constant  with constant Pr and Ec =0,K=1. The  slope of the velocity profiles  increases with increasing the values of   nonlinear parameter.

The figure 8.0 the represents the variation of velocity gradient with nonlinear parameter [n=0,1,2]. The velocity profiles Are decreases with increasing the nonlinear parameter.Thefig.8.0represents the effect of nonlinear parameter on nondimensional temperature distribution 

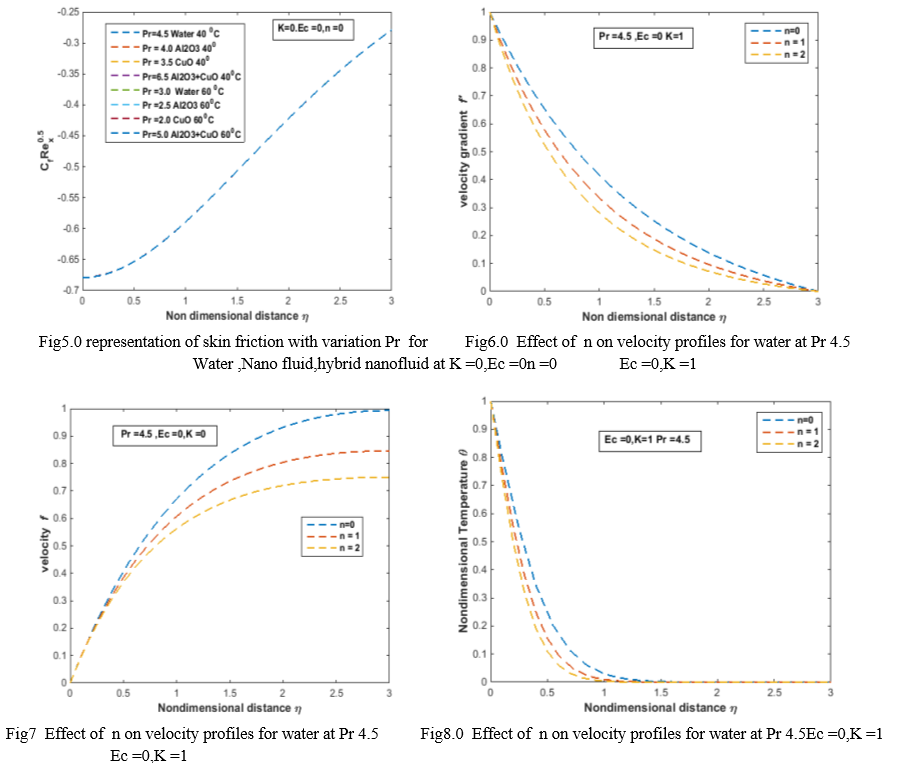
The slope of temperature distribution  is increases with increasing the values of n . Fig 9.0 Fig 10.0 represents the variation of local Nusselt numbers and skin friction values with the variation in nonlinear parameter. The Nusselt numbers are increases with increasing the nonlinear parameter. From the figure10. The skin friction is increases with increasing the values of n.

 Fig 11.0 &12.0 exhibits the variation of velocity and velocity gradient with variation of Eckert number  at [0,1,2]  for water  [Pr =4.5 K=0,n=0].

The velocity profiles have no much significance on velocity and its gradients .Fig13.0 reports the variation of nondimensional temperature with distance with the effect of Ec number at different[Ec  =0,1,2]. The temperature distribution is more with high Ec value. Due to the higher heat flux.  Fig14& 15 represents the variation  of Nusselt and skin friction   variation with nondimensional distance.The Nusselt numbers increases with increasing the Ec number and all the slope of the local Nusselt numbers are merging at the  0.9 from the initial position of the nondimensional distance.

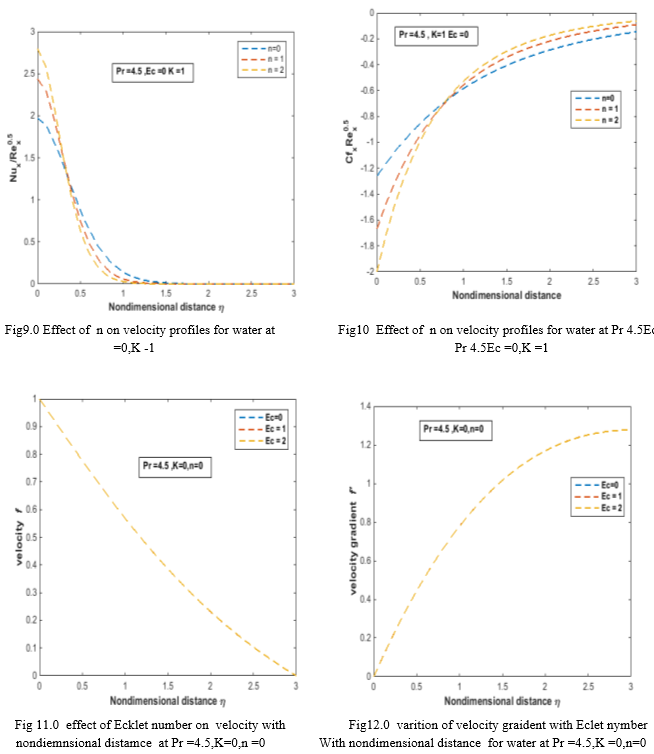
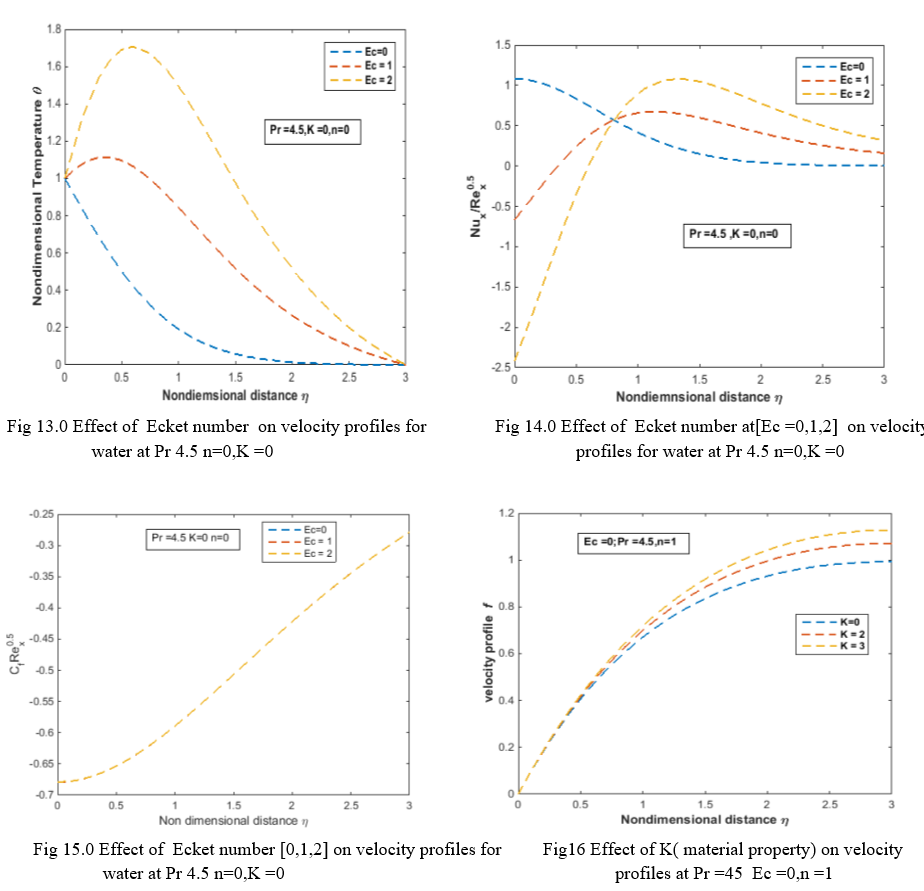
Fig16.0 & Fig17.0 represents the variation of velocity and its gradient  variation with  [K=0,1,2 ]  for Pr number for water [Pr =4.5,Ec =0,n=1] The velocity profiles are  increases with increasing  the values of K.

Fig18. Represents the variation of nondimensional temperature with non dimensional distance for [Pr =4.5 Ec =0,n=1]  the effect of  K have no much significance  on nondimensional temperature .Fig19& 20  represents the variation Nusselt number and skin friction with effect of K  for constant Prandtl number Pr =4.5 n=1 Ec =0 . The local Nusselt numbers have no much significance and friction increases with increasing the value of K.

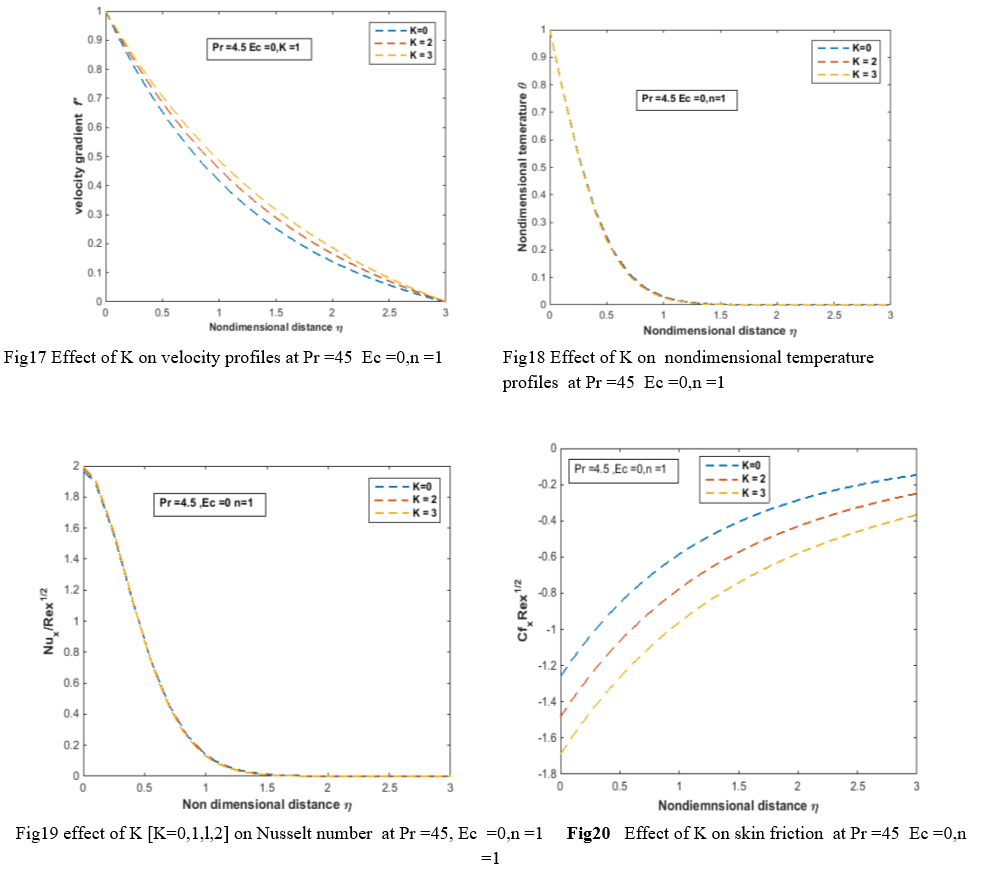
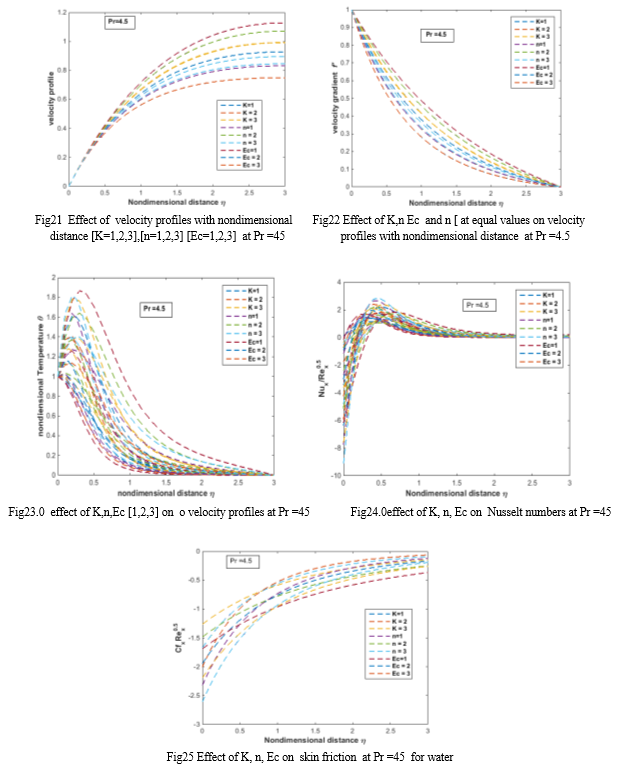
Fig 21& 22 represents the variation of  all parameters K, n, Ec the variation of velocity and velocity gradient at different values of  [K =1,2,3],[n=1,2,3]  Ec=[1,2,3] at constant Pr =4.4 for water.The velocity and velocity gradient are increases with increasing the K ,n, EC, Fig 23 represents the variation of non dimensional numbers with the parametric change of [K ,n, Ec] at the constant Pr 4.5 for water, the temperature profiles are increases with increasing the values of [K, n, Ec]. Fig24 &25 represents the variation of Nusselt number and skin friction for the variation of parametric study  of [K. n, Ec].The skin friction  and Nusselt numbers are increases with increasing the values of [K, n, Ec]

Conclusion

The numerical investigation are carried out the effects of the substance factor ????, the viscous dissipation Ec, the nonlinear stretching parameter ????, and the Prandtl number Pr on the fluid flow and heat transfer characteristics toward a nonlinear stretching sheet immersed in a micropolar fluid. The prandtl number at different temperatures 400C .600C are considered for the water and water based nanofluids (Al2o3,CuO,and hybrid nanofluid. It is found that both the magnitude of the skin friction coefficient and the local Nusselt number increase with the nonlinear stretching parameter ???? and decrease when K increases for fixed values of n and also increases with increasing the n. The nondimensional temperatures increases with increasing the temperature and Pr and velocity profiles and velocity gradient are increases with increasing the Pr. Number. The hybrid nanofluid are better and super nanofluids for increasing the het transfer rate comparatively other convectional fluids

References

[1] Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [2] Eringen, A.C. Theory of thermo micropolar fluids. J. Math. Anal. Appl. 1972, 38, 480–496. [3] Ariman, T.; Turk, M.A.; Sylvester, N.D. Micro continuum fluids mechanics—A review. Int. J. Eng. Sci. 1973, 11, 905–930. [4] Ariman, T.; Turk, M.A.; Sylvester, N.D. Applications of micro continuum fluids mechanics. Int. J. Eng. Sci. 1974, 12, 273–293. [5] Ahmadi, G. Self-similar solution of micropolar boundary layer flow over a semi-infinite plate. Int. J. Eng. Sci. 1976, 4, 639–666. [CrossRef] [6] Eringen, A.C. Micro continuum Field Theories. II—Fluent Media, 1st ed.; Springer: New York, NY, USA, 2001. [7] Be’g, O.A.; Bhargava, R.; Rashidi, M.M. Numerical Simulation in Micropolar Fluid Dynamics; Lambert Academic Publishing: Saarbrucken, Germany, 2011. [8] Rehman, M.A.; Rehman, A.A.; Samad, M.A.; Alam, M.A. Heat transfer in a micropolar fluid along a non linear stretching sheet with a temperature-dependent viscosity and variable surface temperature. Int. J. Phys. 2009, 30, 649–670. [9] Berre, I.; Florian, D.; Eirik, K. Flow in fractured porous media: A review of conceptual models and discretization approaches. Transp. Porous Media 2019, 130, 215–236. [CrossRef] [10] Upendar, M.; Srinivasacharya, D. Mixed convection in MHD micropolar fluid with radiation and chemical reaction effects. Heat Transf. Res. 2014, 45, 1999–2018. [11] Sharma, R.; Bhargava, R.; Singh, I.V. Combined effect of magnetic field and heat absorption on unsteady free convection and heat transfer flow in a micropolar fluid past a semi-infinite moving plate with viscous dissipation using element free Galerkin method. Appl. Math. Comput. 2010, 217, 308–321. [12] Mohammadein, A.A.; Gorla, R.S.R. Effects of transverse magnetic field on mixed convection in a micropolar fluid on a horizontal plate with vectored mass transfer. Acta Mech. 1996, 118, 1–12. [13] Abo-Eldahab, E.M.; El-Aziz, M.A. Flow of and heat transfer in micropolar fluid past a stretching surface embedded in a non-darcian porous medium with uniform free stream. Appl. Math. Comput. 2005, 162, 881–899. [14] Ahmad, F.; Hussain, S.; Ali, M. An analytical solution of MHD flow over porous stretching sheet. J. Basic. Appl. Sci. Res. 2014, 4, 160–167. [15] Dayyan, M.; Seyyedi, S.M.; Domairy, G.G.; Gorji, B.M. Analytical solution of flow and heat transfer over a permeable stretching wall in a porous medium. Math. Probl. Eng. 2013, 2013, 682795. [16] Kartini Ahmad, Anuar Ishak, and Roslinda Nazar.,” Micropolar Fluid Flow and Heat Transfer over a Nonlinearly Stretching Plate with Viscous Dissipation.” Mathematical Problems in Engineering Volume 2013, Article ID 257161, 5 pages Mathematical Problems in Engineering Volume 2013, Article ID 257161, 5 pages. [17] A. Ishak, R. Nazar, and I. Pop, “Post-stagnation-point boundary layer flow and mixed convection heat transfer over a vertical, linearly stretching sheet,” Archives of Mechanics, vol. 60, no. 4, pp. 303–322, 2008. [18] Z. Ziabakhsh, G. Domairry, and H. Bararnia, “Analytical solution of non-Newtonian micropolar fluid flow with uniform suction/blowing and heat generation,” Journal of the Taiwan Institute of Chemical Engineers, vol. 40, no. 4, pp. 443–451, 2009 [19] A. S. Alshomrani and T. Gul, “A convective study of Al2O3-H2O and Cu-H2O nano-liquid films sprayed over a stretching cylinder with viscous dissipation,” Eur. Phys. J. Plus 132(495), 1–16 (2017). [20] M. M. Rashidi, V. N. Ganesh, H. A. K. Abdul, B. Ganga, and G. Lorenzini, “Influences of an effective Prandtl number model on nano boundary layer flow of ?Al2O3-H2O and ?Al2O3-C2H6O2 over a vertical stretching sheet,” Int J Heat Mass Transf 98, 616–623 (2016). [21] U. Khan, Adnan, N. Ahmed, and S. T. Mohyud-Din, “3D squeezed flow of ?Al2O3-H2O and ?Al2O3- C2H6O2 nanofluids: A numerical study,” Int. J. of Hydrogen Energy, 1–14 (2017) [22] T. Hayat, F. Shah, M. Ijaz Khan, M. Imran Khan, and A. Alsaedi, “Entropy analysis for comparative study of effective Prandtl number and without effective Prandtl number via ?Al2O3-H2O and ?Al2O3- C2H6O2 nanoparticles,” J of Molecular Liquids (2018). [23] S. Jain, M. Kumarib, and A. Parmar, “Unsteady MHD chemically reacting mixed convection nanofluids flow past an inclined pours stretching sheet with slip effect and variable thermal radiation and heat source,” Materials Today: Proceedings 5, 6297–6312 (2018).

Copyright

Copyright © 2022 G. SrinivasaRao . This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.