House Price Prediction and Recommendation

Abstract

Data mining is increasingly frequently used in the housing market. In order to estimate house prices, important housing qualities, and many other things, data mining is quite helpful since it can extract pertinent knowledge from raw data. According to research, the real estate market and home owners are frequently concerned about price variations in housing. To analyse the pertinent characteristics and the best models to forecast home values, a literature review is conducted. The analyses\' results supported the usage of the K-Nearest Neighbor and Random Forest Regression as the most effective models when compared to other models. Furthermore, our results imply that structural characteristics and locational characteristics are important predictors of housing prices. To figure out the most significant factors that affect house prices and to recognise the best machine learning model to employ in this field, this study will be of great value, especially to housing developers and academics.

Introduction

I. INTRODUCTION

Along with other fundamental necessities like food, water, and many other things, a place to call home is one of a person's most basic wants. The demand for homes increased quickly over time as people's living standards rose. Although some people buy homes as investments or as real estate, the majority of people purchase homes for habitation or as a means of support.

Housing markets, a key factor in a nation's economy, are said to have a favourable effect on a country's currency. In order to meet housing demand, homeowners will buy items like furniture and household equipment, and homebuilders or contractors will buy building materials, which is a sign of the economic wave effect brought on by the new housing supply. In addition, consumers have the resources to make a sizable investment, and a country's abundant housing supply indicates that the construction industry is in good shape. Every year, there is a growth in the demand for homes, which indirectly drives up home prices. The problem arises when there are numerous variables such as location and property demand that may influence the house price, thus most stakeholders including buyers and developers, house builders.

A. Problem Statement

How well can house prices be predicted by using K-Nearest neighbour and Random forest regression?

II. LITERATURE SURVEY

In order to effectively train a machine learning model, we must analyse several machine learning techniques in this conference paper. The current state of the economy can be seen in home cost trends, which also directly affect buyers and sellers. The actual cost of a property depends on numerous factors. They include things like the number of bedrooms, bathrooms, and location. Costs are lower in rural areas than in cities. The price of a home increases with factors like proximity to a highway, a mall, a super market, employment opportunities, top-notch educational facilities, etc. A few years ago, real estate businesses tried manually predicting property prices. A specialised management team is employed in the organisation to forecast the cost of any real estate asset.

Wang and Wu (2018) claim that Random Forest surpasses Linear Regression in terms of accuracy utilising 27,649 housing assessment price data from Airlington county, Virginia, USA, during 2015. (see also Muralidharan et al., 2018). In order to anticipate housing prices in Petaling Jaya, Selangor, Malaysia, Mohd et al. (2019) use a number of machine learning algorithms based on a collection of characteristics, including the number of beds, floor level, building age, and floor size. In their study, which examines the outcomes from Random Forest, Decision Tree, Ridge Regression, Linear Regression, and LASSO, the researchers come to the conclusion that Random Forest provides the best overall accuracy, as measured by the root mean squared error (RMSE).

Koktashev et al. (2019) make an effort to determine the house values in the city of Krasnoyarsk using 1,970 property transaction records.

According to their research, aspects of a home include its number of rooms, overall area, floor, parking, kind of repair, number of balconies, type of bathroom, number of elevators, garbage disposal, year of construction, and accident rate. To forecast real estate values, it uses random forest, ridge regression, and linear regression. According to their analysis, random forest outperforms the other two algorithms in terms of mean absolute error (MAE).

III. METHODOLOGY

The prediction accuracy of the algorithms k-NN and Random Forest has been evaluated in order to determine which machine learning approach is best to employ for the house price problem. For this investigation, algorithms from the scikit-learn library were employed rather than being created from scratch. It is a cutting-edge library that is a component of the scikit collection of Python scientific toolkits. The data analysis library Pandas from "Our Python" was also used. The data set has been pre-processed and cleaned in order for the algorithms to accept the data as input prior to comparing the methods. Additionally, a method for analysing the data has been developed. Finally, the machine learning algorithms have been evaluated with various values for the pertinent hyperparameters for prediction and run on the cleaned data set.

A. Cleaning Data

Most machine learning algorithms are set up to only accept input in the form of numeric data. The Ames Housing data collection contains more than half of non-numerical columns that need to be encoded, in this case utilising one-hot encoding and labelling. Additionally, different columns have different methods for handling empty values as detailed in section 3.1.3.

B. Normalizing Data

The data set's numerical variables have a wide range of possible values, and depending on the column, these ranges can vary significantly. Scaling the data to the range [0, 1] through normalisation has prevented bias from being introduced. Although there are alternative options, the Euclidean norm has been employed in this work to normalise the data. The formula for calculating the Euclidean norm, or ||x||2, is as follows: ||x|| + + xn 2 where x1 xn are all the values of a feature in the data set. After that, each feature value is normalised by being divided by the Euclidean norm. Since all non- numeric features are converted to numeric in the following section, normalisation with the Euclidean norm has been applied to all features in the data set.

C. Encoding Categorical Data
Numerous variables in the data set are categorical and only accept a small range of values. For instance, the nominal variable "Street" can have the values "Grvl" for gravel roads and "Pave" for paved roads, indicating the type of road access to the property. Conventional machine learning algorithms cannot read such categorical values without first pre-processing them into a numerical format. The data collection contains ordinal and nominal category variables of different sorts. The ordinal variables are different because there is some sort of inherent ordering between them. For instance, the Land Slope variable uses three values—gentle, moderate, or severe—that are logically arranged to classify the slope of the property. Labeling is the straightforward process of associating a numerical value with each of the ordinal values in order to maintain the ordering. Simply assigning integer numbers beginning with 1 for the lowest order value, 2 for the next, and so forth, will do this. Figure 3.1 shows an illustration of four randomly selected entries from the data set and one possible encoding scheme.

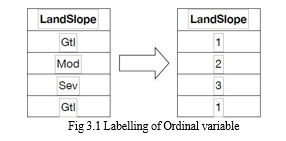
For variables with a high cardinality, or numerous alternative values, one-hot encoding may be a challenge. The problem is that it might produce far too many columns to be useful. Most nominal variables in the Ames data set have values between five and 10, and the majority of them have less than 20. As a result, one-hot encoding has been applied to everyone.

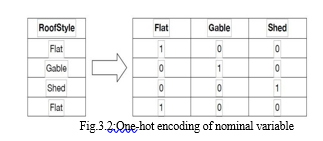
D. Missing Values

The pre-processing has taken care of values for data set elements that are empty since they are useless for the model. Fortunately, there aren't many missing values in the data set, which is mostly complete. The processing of these has varied depending on the column. There are numerous "NA" values in the nominal and ordinal columns. Pandas sees this as an empty cell by coercion, although the Data Documentation states that the value "NA" really denotes the absence of a feature rather than its uncertain status. For instance, for the majority of properties, the columns "PoolQC," an ordinal variable describing the pool's quality, and "PoolArea," have the value "NA," indicating that there is no pool rather than that the information is unknowable. Therefore, "NA" is not considered an empty value for these columns.

E. Prediction and Evaluation

The machine learning models have been put to the test using data with known property prices in order to compare them. As a result, training and testing data are separated from the data set. The bigger portion of the split data set is made up of training data, as the name implies, which is utilised to train the machine learning model. The sales price of the properties is known to the model when it is fitted with the training data, allowing it to learn from the data. To evaluate how successfully the machine learning model forecasts home prices, testing data is used. To forecast the price for the properties given their various qualities, the machine learning model is given the test data but not the properties' prices. The actual price in the test data is then contrasted with the forecasted price.

F. Splitting the Data
There are two uses for the data set. We divided the data set in two for the purposes of training and testing the algorithm, respectively. Care must be used while choosing the proportion of rows in the training and test sets. The conclusion is less believable if the test data is too limited because a wide range of rows are not evaluated. While increasing the quantity of the test data increases dependability, doing so also decreases the number of rows in the training data, which makes the model less accurate. Cross-validation is a technique that can be used to reduce the elects of a bigger test set, and it was in this experiment. By using different portions of the data set as test data, the model is run several times on the data set as part of the cross-validation process. It is standard procedure to utilise fivefold cross validation, which involves using 20% of the data set for testing and alternating it for five runs. The first 20% of the data set is utilised for testing, while the remaining 80% is used for training, on the first run. The following 20% is used as testing data on the second run, and so forth.

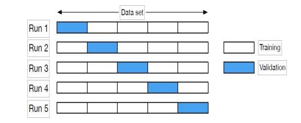
G. Algorithm hyperparameters

Numerous hyperparameters have a direct impact on how the k-Nearest Neighbor and Random Forest algorithms function and, consequently, how well they forecast outcomes. In contrast to parameters that are obtained during training, a hyperparameter is a parameter for the algorithm that is established before computing.

H. k-Nearest Neighbour Regression

The hyperparameters "k" and "weights" for the k-Nearest Neighbor algorithm have been examined to see which results in predictions with the least amount of error. Remember from section 2.1.1 that the 'k' hyperparameter controls the number of neighbours to take into account when calculating the target value. In this study, k-values ranging from 1 to 10 are tested. The options for the "weights" hyperparameter are "distance" or "uniform." When determining the target value for the sample being predicted, the neighbouring target values (the sale price) are weighted by distance using the value "distance." The value "uniform" denotes that the target value is determined without weighting the values of the neighbours.

I. Random Forest Regression

The 'n estimators','max features', and 'criterion' tested hyperparameters for the Random Forest method were all added in section

The number of trees to utilise in the model is determined by the hyperparameter 'n estimators'. We test up to 50 tree values. The'max features' parameter, which determines how many features will be used to construct the Random forest trees, will be tested with values ranging from 1 to all of the features in the dataset (221 after cleaning and including one-hot encoded features). When building the trees in the Random forest, the function that assesses the quality of splits is set using the 'criterion' hyperparameter.

J. Algorithm comparison

The emphasis of this study is finally reached when mistakes of the k- Nearest Neighbor and Random Forest algorithms are compared. The errors for the corresponding algorithms running on their chosen optimal hyperparameters are shown in the table below. The Random Forest approach clearly outperforms the k-Nearest Neighbor algorithm in terms of predicting with the minimum error across all four error metrics examined.

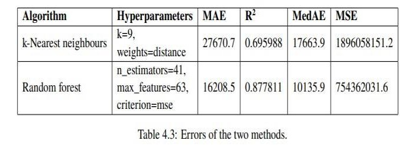
Conclusion

According to the paper \"House Price Prediction and Recommendation\" Using Machine Learning,\" it is possible to anticipate the price of a house based on a variety of attributes on the provided data. The Random Forest method fared the best across all error metrics, according to our main finding. The MAE and MedAE of this approach are both roughly half of the corresponding errors for the k-Nearest Neighbor algorithm. Additionally, Random Forest\'s R2 value is higher than K- NN\'s, indicating that it will be able to predict future data more accurately. The R2 score for Random forest is fairly good because an R2 value close to 1 is better in terms of how well the models fit the data. This is in line with the findings of Baldominos, who found that Random forest outperforms K-NN even if our models were more accurate in terms of error metrics. How accurately property prices can be predicted using k-Nearest Neighbor and Random Forest Regression is the research issue for this study. In this study, we discovered that the Random Forest Regression Algorithm outperforms the k-Nearest Neighbor Algorithm at predicting property values. The real prices in our testing data and the prices predicted by the Random forest regression technique still differ, though. The Random forest model had the lowest error, with an MAE of $1,6208.5, or nearly 9% of the mean price.

References

[1] David Donoho. “50 Years of Data Science”. In: Journal of Computational and Graphical Statistics 26.4 (2017), pp. 745–766. url: https: // doi.org/10.1080/10618600.2017.1384734. [2] Sameerchand Pudaruth. “Predicting the Price of Used Cars using Machine Learning Techniques”. In: International Journal of Information & Computation Technology 4 (Jan. 2014). [3] Alejandro Baldominos et al. “Identifying Real Estate Opportunities Us-ing Machine Learning”. In: MDPI Applied Sciences (Nov. 2018). [4] Johan Oxenstierna. Predicting house prices using Ensemble Learning with Cluster Aggregations. 2017. [5] Wikipedia. k-nearest neighbors algorithm. https://en.wikipedia. org/wiki/ K-nearest_neighbors_algorithm. Accessed: 2019-04-21. [6] Antonio Mucherino, Petraq J. Papajorgji, and Panos M. Pardalos. “kNearest Neighbor Classification”. In: Data Mining in Agriculture. New York, NY: Springer New York, 2009, pp. 83–106. isbn: 978-0-387-88615-2. url: https://doi.org/10.1007/978- 0- 387- 88615-2_4. [7] Trevor Hastie, Robert Tibshirani, and Jerome Friedman. The elements of statistical learning: data mining, inference and prediction. 2nd ed. Springer, 2009. url: http : / / www - stat . stanford. edu / ~tibs/ElemStatLearn/. [8] Wikipedia. Random forest. https : / / en . wikipedia . org/wiki/ Random_forest. Accessed: 2019-04-25. [9] Scikit-learn API Reference. sklearn.ensemble.RandomForestRegressor. https://scikit-learn.org/stable/modules/generated/ sklearn.ensemble.RandomForestRegressor.html. Ac-cessed: 2019- 04-25.REFERENCES

Copyright

Copyright © 2023 Payal Mahajan, Mayur Gawade, Aniket Patel, Shantanu Barhanpurkar, Onkar Deshmukh. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.