Ijraset Journal For Research in Applied Science and Engineering Technology

Abstract

Sound causes image degradation during detection, processing, signal processing, and transmission through sound channels. Noise removal is a technique for eliminating noise from photographs. Denoising refers to the process of removing noise from a picture. In this paper we have proposed a novel algorithm was built based on a variable called \"contourlet transform\" is a term used to describe the transformation of a contourlet This algorithm is significantly more effective. in image extraction than the wavelet technique and especially the shock wave\'s elimination. The parameters were set. when wavelet and contourlet are compared SNR and IEF transforms The findings show that in terms of performance, the suggested approach outperforms the wavelet

Introduction

I. INTRODUCTION

Many forms of noise, such as salt and pepper noise, Gaussian noise, Poisson noise, and Speckle noise, can contaminate digital pictures. Noise is often accumulated during image capture and transmission. The random occurrences of black and white pixels in photographs are known as salt and pepper noise, while Gaussian noise is statistical noise with a probability density function equal to that of the normal distribution, often known as the Gaussian distribution. In picture denoising, the wavelet transform works effectively. The stationary wavelet transform (SWT) and the translation invariant wavelet transform (TIWT) produce smaller mean-square-errors than the regular wavelet transform, and image reconstruction using SWT or TIWT is perceptually more delicate and smoother with much less observable art if compared to the regular wavelet transform. However, because the 2D wavelet transform employed in image processing is essentially a tensor-product implementation of the 1D wavelet transform, it fails to keep directional edges in pictures and is ineffective in portraying contours (curves) that are neither horizontally or vertically oriented. Curvelet was created in an attempt to better effectively represent curves. However, implementing the curvelet transform in discrete form is not straightforward. Thus, a contour let transform is proposed for image denoising to circumvent this novel technique. Laplacian pyramid and two-dimensional directional filter banks are used to perform the contourlet transform, which may hold multi resolution, localisation, virtually critical sampling, variable directionality, and anisotropy all at the same time. Consider an input signal x(t) and a noisy signal n in the image denoising process (t). To get noisy data, combine these elements.  y(t)

                   y(t)=x(t)+n(t)  …………..(1)

Coutourlet is a two-dimensional picture representation method that uses actual data. The transform is made up of two layers of filters: Multi-scale decomposition is achieved using the Laplacian pyramid transform, and multi-direction decomposition is achieved using a directional filter bank. Contourlet transform allows for flexible multi-resolution and multi-direction decomposition while retaining the image's basic feature. Unlike curvelet transform, contourlet transform starts with a discrete domain digital conversion, then extends to a continuous domain and analyses its attributes. It may be more convenient to display the simulation in this manner. The images utilised in this project for experimentation are all gray-scale photos. They are devoid of any colour information. They represent the image's brightness. This picture has eight bits per pixel, which implies it may have up to 256 brightness levels (0-255). A '0' symbolises black, whereas a '255' denotes white. The multiple grey levels are represented by values ranging from 1 to 254. Intensity pictures are sometimes referred to as intensity images since they carry the intensity information.

II. LITERATURE REVIEW

Noise in digital photographs is discovered to be additive white Gaussian noise (AWGN), which has a Gaussian probability distribution and has uniform power throughout the whole bandwidth. AWGN has traditionally been reduced by linear spatial domain filters like the Mean filter and the Wiener filter [3,4,5]. The spatial mean filters are a type of sliding window filter that substitutes the computed mean value for the centre value. Linear approaches are mathematically simple, but they have the drawback of causing blurring. They also don't work well when there's signal-dependent noise present.

Klaus Rank and Rolf Unbehauen [6] devised an adaptive standard recursive low pass filter that evaluated the three local image attributes edge, spot, and flats as adaptive areas with Gaussian noise. In many circumstances, employing linear filtering to remove noise from a picture causes blurring.

To overcome the aforementioned drawbacks, nonlinear filters [5] are designed. Because the spatial relations of the grey values of neighbour pixels may detect the objects in an image, nonlinear filters govern the direction and/or degree of averaging with the local contents of neighborhood pixels. The median filter is a well-known nonlinear filter. Tukey [7] invented the median filter in 1970. The median filter is currently widely used to reduce noise and smooth pictures. The difficulty with a simple median filter is that it only works well for suppressing low-density impulsive noise. To enhance the ordinary median filter, Hakan et al.[8] employed a topological median filter. The topological median filters outperform ordinary median filters in terms of keeping edge sharpness. Yanchun et al. [9] developed an image denoising technique based on an average filter with maximizing and minimization for smooth areas, a unidirectional Median filter for edge regions, and a median filter for indefinite regions. Picture deterioration due to blurring or artefacts caused by a filtering scheme is not acceptable when constructing a filtering technique for image data. The following requirements should be met in the ideal situation:

1. Preserve object boundaries and detailed structures to reduce information loss.
2. Effectively eliminate noise in areas with similar physical features. Recent advancements based on bilateral filtering solve the fundamental disadvantages of traditional spatial filtering and considerably increase image quality while meeting the above-mentioned main requirements 1.

III. PROPOSED WORK

The Contourlet transform is a directed transform that could capture contour and fine features in an image. The discrete domain creation is followed by sparse growth in the continuous domain in this transformation. The primary distinction between Contourlet and other transformations is that it employs the Laplacian pyramid [4,5] as well as the Directional Filter Banks [1, 3]. As a result, not only are edge discontinuities detected, but they are also converted into continuous domains. The Contourlet Transformation is depicted in the diagram below, where the input picture has frequency components such as LL (Low Low), LH (Low High), HL (High Low), and HH (High High)

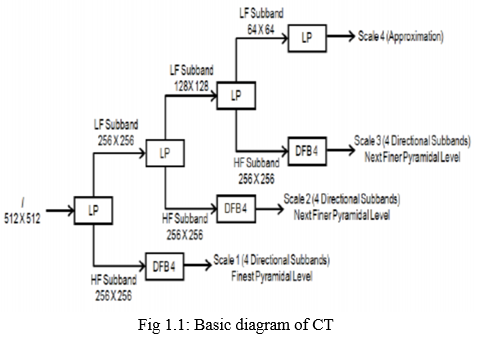
A. Algorithm description

1. The process starts with the noisy image.
2. The decomposition procedure is used to turn this image into the Contourlet Transform domain. The coefficients are determined in Wavelet using scaling and a wavelet filter. However, in Contourlet, we use non-separable filter banks to construct discrete-domain multiresolution and multi-direction Using contour sectors and the so-called Contourlet transform, this architecture produces flexible multiresolution, local, and directed picture expansion.
3. Thus from the decomposition process the coefficients are determined.
4. Then for each noisy image pixels, the variance is estimated.
5. The resultant values are then compared with a threshold value to determine whether the pixel is corrupted or not.
6. If the pixels are corrupted, they are suppressed or modified. Otherwise the pixels are preserved for further process.
7. Then all the resultant coefficients are reconstructed which results in denoised image.

B. Thresholding

Generally for denoising, the coefficients of the noisy image are compared with the threshold value. These threshold values are either obtained by trial and error method. Since human eyes are very sensitive to intensity of neighboring pixel values, in image denoising techniques, the variance in homogeneous regions must be less. Considering the threshold values depending on the variance, the noise level in the corrupted image still decreases. In this algorithm, a threshold value is set based upon the variance of the corrupted image. Based upon the results from various variance levels (nvar), the threshold is fixed. The intensity of the noise being added to the image (th) and the standard deviation of the noise less image (sigma) are also the deciding factors in fixing the threshold values. Based upon the various results obtained, we deduce that the threshold values must be fixed depending upon the high noise level and low noise level. In Speckle noise, the default variance level is 0.04, so considering Speckle noise variance (nvar) above

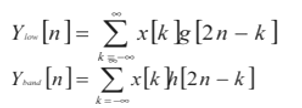
as high noise level and below 0.05 as low noise level, we introduced two threshold values separately. The results also prove that this two separate threshold values improve the denoising ability of the algorithm. Now to reconstruct the image, the coefficients above the threshold values are retained for Contourlet reconstruction and the coefficients below the threshold values are suppressed. The retained coefficients are reconstructed to obtain the Denoised image. This process is shown in the figure 2.1.

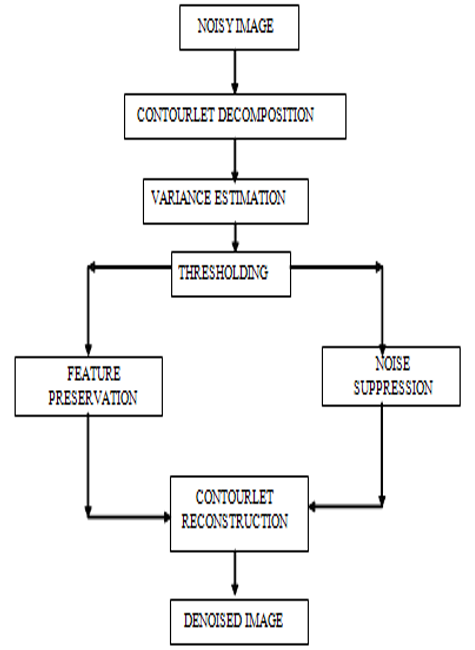
IV. RESULT

For denoising, the standard test picture is used. PSNR, MSE and Visual quality assessment are the evaluation metrics used to compare Wavelet with the proposed technique employing Contourlet Transform. Have used three noises and also an additional noise level feature has been added to the project. The output parameters have been observed with different noise levels. The denoised image is obtained at the output. GUI has been provided in the project for proper accessibility.

Table 1.1 Output result for denoised image

The contourlet  transform is thus an efficient denoising system for images

Conclusion

The elimination of noise from images is covered in this study. As a result, the novel suggested Contourlet transformation-based approach is shown to be more efficient than the wavelet algorithm in Image Denoising, notably for noise removal. This is based on a test image that has been corrupted with gaussian, Rayleigh, and Rician noise with different noise levels such as 5, 10, 15, and 20. In terms of PSNR, MSE values, and visual viewpoint, the obtained findings in qualitative and quantitative analysis suggest that the proposed method outperforms the wavelet. MATLAB 10 R2007b is used to implement the algorithms.

References

[1] W.Y. Chan, N.F. Law, W.C. Siu, “Multiscale feature analysis using directional filter bank,” Proceedings of the 2003 Joint Conference of the Fourth International Conference on Information, Communications and Signal Processing, December 2003, pp. 822-826. [2] M. N. Do and M. Vetterli, “Contourlets: a Directional Multiresolution image representation,” Proceedings of 2002 IEEE International Conference on Image Processing, vol. 1,2002, pp 357-360. [3] M. N. Do and M. Vetterli, “Pyramidal directional filter banks and curvelets,” Proc. IEEE Int. Conf. on Image Proc., vol. 3, 2001, pp. 158-161. [4] P. J. Burt and E. H. Adelson, “The Laplacian pyramid as a compact image code,” IEEE Trans. Commun., vol. 31, no. 4, 1983, pp. 532– 540. [5] Zhiling Longa, b and Nicolas H. Younana “Denoising of images with Multiplicative Noise Corruption”, 13th Europian Signal Processing Conference, 2005,,a1755. [6] Arivazhagan, S. “Some studies on texture image analysis using wavelet transform and its usage in few industrial applications”. Ph.D. Thesis.2004 [7] Kun Liu , Lei Guo, “Algorithm of image fusion based on finite ridgelet transform”, Proceedings of SPIE - The International Society for Optical Engineering, v 6786, MIPPR 2007: Automatic Target Recognition and Image Analysis; and Multispectral Image Acquisition, 2007 [8] Fu-Chiang Tsui, Ching-Chung Li, Mingui Sun, Sclabassi, R.J. “A comparative study of two biorthogonal wavelet transforms in time series prediction” Systems, Man, and Cybernetics, 1997. \'Computational Cybernetics and Simulation\'., 1997 IEEE International Conference on Volume 2, 12-15 Oct. 1997 [9] Xia Jun Jun, Ni Lin; Miao, Y. “A new digital implementation of ridgelet transform for images of dyadic length” Information Technology and Applications, 2005. ICITA 2005. Third International Conference onVolume 1, 4-7 July 2005 Page(s):613 - 616 vol.1 [10] Jean-Luc Starck, Candes E.J, Donoho D.L. “The curvelet transform for image denoising”. Image Processing, IEEE TransactionsonVolume 11, Issue 6, June 2002 Page(s): 670 – 684 [11] Arivazhagan S., Ganesan L., Subash Kumar T.G. “Texture classification using ridgelet transform”. Computational Intelligence and Multimedia Applications, 2005. Sixth International Conference on 16-18 Aug. 2005 Page(s): 321 – 326 [12] Singh M., Mandal M., Basu A. “Visual gesture recognition for ground air traffic control using the Radon transform”.Intelligent Robots and Systems, 2005. (IROS 2005). 2005 IEEE/RSJ International Conference on 2-6 Aug. 2005

Copyright

Copyright © 2022 Smita Vasant Tempe, Asst. Prof. Ruhina Quazi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.