Using the Area of Contact between Layers as a Predictor for the Anisotropic Strength of Parts Produced by FDM

Abstract

Fused Filament Fabrication (FFF), better known as FDM© (Fused Deposition Modeling) is an additive manufacturing process (AM) by which a physical object can be created from a 3D model generated in the computer, through layer-by-layer deposition of semi-melted plastic filaments. However, parts produced by the FDM process have different characteristics compared to parts produced by traditional methods such as plastic injection, especially with regard to mechanical properties related to stresses (tensile, compression, torsion and shear), due to the anisotropic nature of the process deposition. Many works have been carried out in order to determine the influence between the FDM process parameters and the mechanical characteristics of parts produced by this technology. Traditionally, the studied parameters comprise those that are adjusted in slicing software, which does not satisfactorily reflect the bond between the layers. This work uses the area of contact between the layers as the determining factor of the transverse tensile strength to bedding and suggests a methodology for the determination of this parameter. Using analysis of variance (ANOVA) and the Taguchi analysis method, we identified the contact area between the layers as the most relevant parameter for tensile strength in the transverse direction of the printed layers with a relevance of more than 95% over the others investigated parameters. From the survey of relevant properties, new tests were carried out to determine a mathematical model to predict the minimum slicing parameters that should be used to obtain the required strength.

Introduction

I. INTRODUCTION

Additive manufacturing using the FDM (Fused Deposition Modeling) method has been widely used as a quick and cheap way to produce prototypes and is increasingly present in industries, which see this technology as a cheap, efficient and personalized form of production. There are many plastics used in FDM: ABS, PLA, Nylon, PET, composites etc. This technology has also been applied in medicine, engineering, cooking, etc. 3D printers became popular after the fall of the original patent and the creation of open-source models. In this process, a digitally created model is submitted to a slicer software that converts it into instructions for the 3D printer. This is done by dividing the object into layers (slices). A molten plastic filament is then deposited by a fine nozzle, layer by layer on the 3D printer table, ultimately resulting in the projected physical model. This layer-by-layer deposition process allows the manufacture of extremely complex parts, but its mechanical properties significantly differ from parts produced by other methods such as injection, molding, milling etc, especially in the transverse direction of layer deposition. Also, printing via FDM is generally slow. Thus, it is customary to control the percentage of filling of the inner part of the layers in order to reduce printing time and save material. With this, an apparently solid object is produced, but hollow, with the interior filled with a checkered or honeycomb structure, for example. The tensile strength of a PLA printed part, even in the longitudinal direction of deposition and with 100% filling, is 48% lower than a part manufactured by injection molding [1]. The properties of the parts produced by FDM also differ from the properties of the plastics that are used, with regard to mechanical resistance related to traction, compression, deformation and torsion. Especially with regard to tensile strength, this property is not only controlled by the material properties, but significantly, by the layer-by-layer production process, which produces an anisotropy across the layers [2]. The tensile strength is greater when the filament deposition direction coincides with the load application axis [3]. The deposition temperature, layer height, deposition orientation and the presence of air-gap affect the tensile strength according to studies carried out by several authors [4] [5] [6]. Proper selection of FDM process properties can, in theory, produce parts with desired mechanical properties[7]. The characterization of the strength of parts produced by FDM in relation to different printing parameters has been studied by many authors, especially for ABS with specimens produced in the deposition direction (X-Y) [2] [4] [8][9][10][11].

Even to assess the anisotropy present in the transverse printing direction (Z), many authors simulate this anisotropy by printing the specimens in the X-Y direction. This technique adds to the resistance between layers, undesirable characteristics that are not present when printing vertically [12][13][14][15][16]. Few authors have studied anisotropy using vertically printed specimens [16][17][18]. But these studies use ASTM638 type I or IV [19], flat dog-bone geometry, which also brings unwanted effects related to deceleration and rapid change in the deposition direction caused by the rectangular cross-section of this geometry. The shape and size of the inner area of these specimens also make it difficult to study the contribution of the perimeter-infill relationship to the strength between the layers. An alternative geometry for specimens is used in this work as suggested in [20]. The main parameters for printing preparation related to the connection between the layers are: The number of perimeters, infill percentage, layer height, extrusion temperature and presence of "air-gap" [21] [17][22][23][24]. But the main factor that defines the resistance between the layers is the contact area between them, which can vary depending on the number of perimeters, infill percentage and infill pattern. However, the characterization of strength in relation to the number of perimeters (an integer parameter) and the percentage of infill does not produce a safe relationship to aid a project in determining the maximum tensile value tolerated by a part to be manufactured by FDM.

This work aims to solve this problem, providing a mathematical expression capable of determining whether the projected geometry for a part to be printed with PLA is capable of supporting the required tensile load and what are the minimum slicing parameters that should be used to obtain the required resistance.

II. METHODOLOGY

In the deposition direction, the perimeters of a piece are the most important connection between the layers, especially in a 100% vertical bed, when there is no lateral displacement between the layers (staircase effect). The greater the number of perimeters, the greater the connection between the layers. The infill percentage contributes little to the vertical strength when done at different angles in the subsequent layers (Fig 1), although it contributes a lot to the structural strength to lateral compression and serves mainly as support for the upper closing layers of the printed piece. There are several infill patterns available in slicers, such as linear, crisscross, grid, honeycomb and others. On the other hand, a linear filling with a single angle not only contributes in the same way to the longitudinal strength and as a support element for the closing layers, but also adds a controlled contact area similar to those of the perimeters (Fig 2). Current versions of slicing softwares allow you to adjust different properties for inside and outside perimeters and for the infill. In this work we will use a linear infill with a single angle and the deposition width (EW) the same as the perimeters.

A. The Layers Bond

Slicing software allows you to adjust the number of perimeters and the infill percentage for the layers but does not show the resulting effective area of contact between the layers. In order to obtain the effective area of contact between the layers, the total length of the deposited wires (L) and the width of the contact bond between the wires (Wb), must be calculated for both the perimeters and the linear infill. Thus, the effective contact area will be:

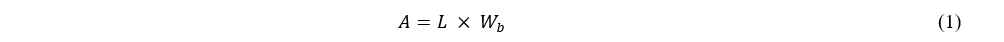
B. The Length of the Deposited Wires

The deposited wire length value (L) is taken from the gcode file generated by the slicer for different percentage infill values. A program created in .NET C# by the author reads the generated gcode file for the specimen and calculates the length of the printhead movements for the perimeters and infill rods. These values are extremely important not only to determine the true infill percentages, as well, as we will see later, the effective fusion area between the layers, necessary to calculate the true ultimate Stress value (Fig 3).

C. The width of the Deposited Wires

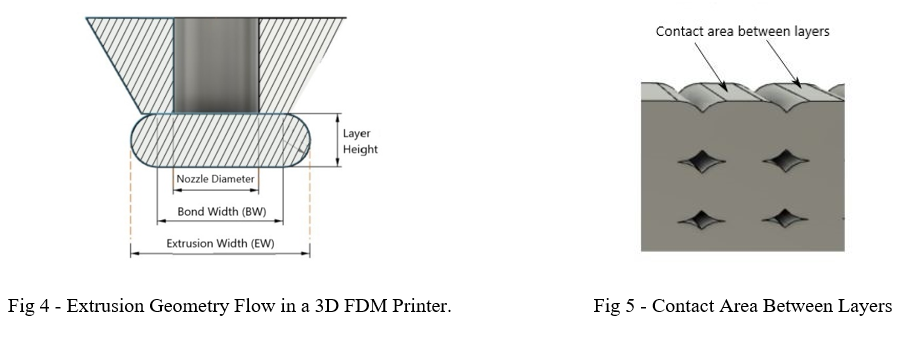
In the 3D FDM printer the melted filaments leaving the extruder nozzle are compressed against the lower layer, flowing laterally in a direction transverse to the extruder speed, forming an oval cross-section, as shown in Fig 4. The ends of this cross-section are assumed to be circular because the surface tensions must act in such a way as to minimize the surface area [25].

The Extrusion Width (EW) is a parameter of the slicing software and it defines the width that the resulting wire will be extruded. It also defines the separation between the centers of filaments deposited side by side, such as the perimeters. The amount of plastic extruded by the extruder is calculated to produce a crushed wire between the layers in order to increase the “bond width” that defines the adhesion area between the layers (Fig 5). It must be said that other parameters, such as the Extrusion Multiplier, can force more plastic to be extruded, in order to increase the lateral contact between wires (perimeters for example) reducing the empty space between the deposited wires (air-gap) [26].

To determine the width of the contact bond (Wb), which represents the transverse dimension of the effective contact between the filaments of two overlapping layers aligned vertically, with a tilt angle equal to zero (Fig 2), a photographic process associated with an image measurement software was used. With a digital microscope, photographs were taken of cross-sections performed on the printed specimens (Fig 6) and the ImageJ software [27] was used to measure the contact line between the layers. Measurements were taken both on photographs of specimens after tensile tests. To obtain a clean cut without introducing mechanical and thermal stress to the cut region, the method that best met our needs was the use of a very thin blade, 0.07mm thick, with a very fast force applied transversely to the layers. For each combination of parameters (layer thickness, extrusion width EW and temperature) different images were taken, in different cross-sections, with 20+ measurements (Fig 7).

III. EXPERIMENTAL SETUP

A. The Process Parameters

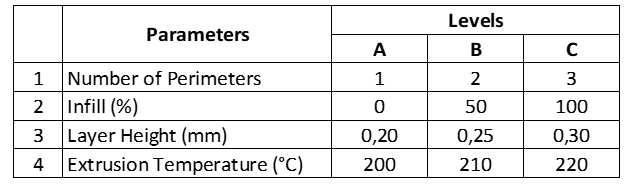
The main slicing parameters related to transverse strength are the number of perimeters, infill percentage, layer height and extrusion temperature. For this research, printed specimens with the parameters listed in the TABLE I were initially tested. Cylindrical specimens with special geometry (Fig 8) [20] were printed on a Makerbot Replicator 2 printer (Fig 9) and tested on custom tensile testing machine [28].

TABLE I - Levels of Selected Parameters

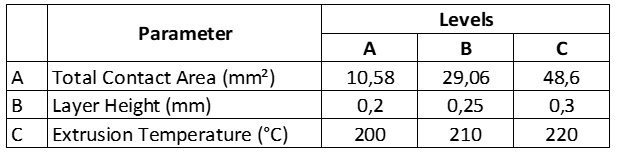
However, to meet the objectives of this research, the parameters Number of Perimeters and Infill Percentage were replaced by a parameter named Total Contact Area calculated by equation (1). For each combination of values shown in the TABLE I, the Infill Percentages were adjusted to produce the Total Contact Areas used as ranges as shown in the Table II

Table II Parameters Levels.

B. The Design of Experiment (DOE)

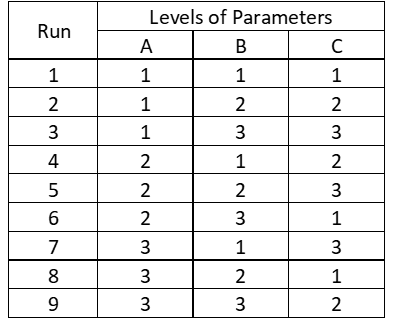
Taguchi's Design of Experiment method was used to evaluate the contribution of the listed process parameters to the longitudinal tensile strength of specimens printed on PLA via FDM [29]. The Taguchi method is a methodology recognized worldwide for the efficient planning of experiments that includes the simplification of experimental planning, reducing the number of experiments needed and yet provide complete information on all factors that affect the influence of parameters. The Taguchi Design of Experiment method makes use of Analysis of Variance (ANOVA) and Signal to Noise Ratio (S/N) and “Main Effect” plots to determine the significance of the factors involved in the process. Given the number of parameters and the degrees of freedom of the experiment, an L9 orthogonal matrix was chosen (Table III).

Table III - Orthogonal L9 Experimental Plan.

IV. RESULTS AND DISCUSSIONS

A.  Contact width

The mean value and standard deviation were then calculated for the bond width (Wb) measurements on the tested specimens. The results are summarized in the TABLE IV. Bond width measurements were also performed on vertical walls printed on different 3D printers, with different brands of PLA and slicing software. The results were compatible with the measurements performed on our specimens.

TABLE IV - Mean Measured Values for Bond Width.

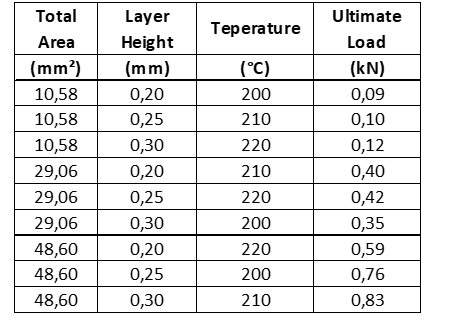
Five specimens of each combination were printed and the average of the ultimate tensile load for the 5 tests was taken. The results are shown in Table V.

Table V

Table V - Experimental Results for the L9 Orthogonal Array.

B. ANOVA and S/N ratio

The purpose of Analysis of Variance is to determine which of the input parameters is statistically significant and their contribution to the output variable while the signal-to-noise ratio measures the sensitivity of the investigated parameter to uncontrollable factors in the experiment. In this experiment the calculation of S/N was done using the “larger is better” approach. The MINITAB 17 software was used to perform the ANOVA and the Taguchi Model Analysis. In the Fig 10 the ANOVA result is shown using the values from the

Table V

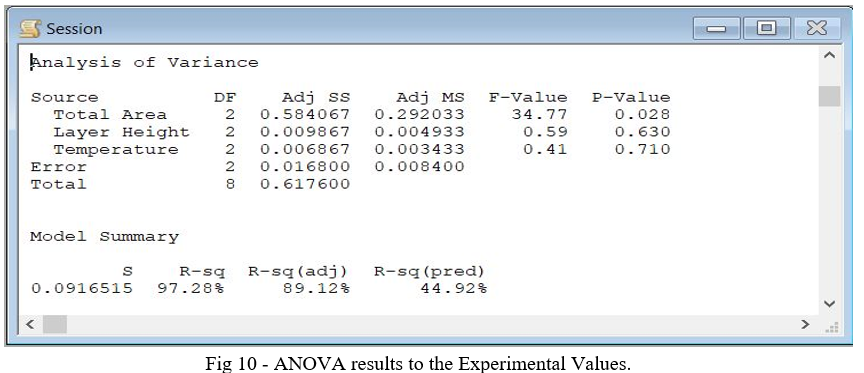
ANOVA uses the F statistic to see how statistically significant the term is. A large F value, F>4, [30] implies that a change in parameter significantly affects the output variable studied. In our result, the Total Area parameter has an F test value of 34.77 which agrees with the hypothesis that this parameter, among the analyzed parameters, is the one that most affects the tensile strength in vertical bedding. The p-value term is calculated from the F-test and presents a value < 0.05, which corroborates the hypothesis of this association, adjusted for a 95% confidence level in all intervals. To quantify the fit of the model to the given values, we must check the values of the quality statistics S and R². The value of S is related to how well the model fits the data and describes the response. The smaller this value, the better the fit. The value of the variation in the response that is explained by the model is represented by the value of R². The higher this value the more adjusted the model is [31].

The percentage value of the contribution of each factor to the tensile strength is obtained by the ratio between the adjusted sum of squares (AdjSS) calculated for the parameter and the total AdjSS value. The Total Area parameter is the one that contributes the most to the tensile strength, with a 95% contribution. The contribution of the Layer Height and Temperature parameters appears with values below 2%.

In Fig 11 we have the “Main Effect Plots” obtained from the Taguchi Method Analysis, which allows us to determine the relationship of the parameters with the tensile strength, based on the calculated signal-to-noise (S/N) ratio. According to the analysis carried out, the best tensile strength values are obtained for the highest values of the S/N ratio.

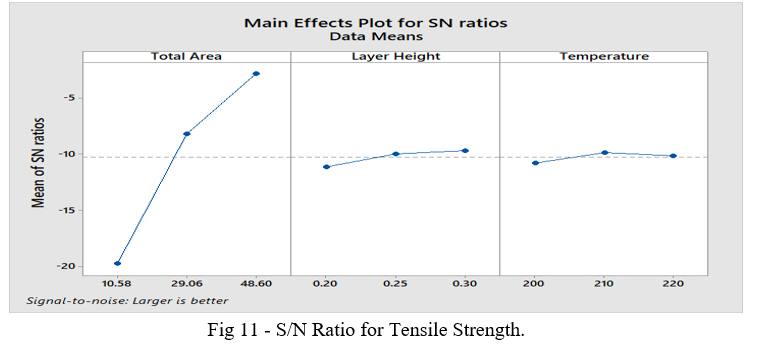
We can observe that the S/N ratio increases substantially with the variation of the Total Area and, although the Layer Height and Temperature parameters present a very small S/N variation, corroborating the low contribution of these parameters to the tensile strength, this variation shows that the greatest tensile strength is obtained with the Total Area of 48.6 mm², with the Layer Height of 0.3 mm and with the Temperature of 210°C.

For the Temperature, it is known that this parameter is related to the printing material, but also to factors related to the environment, the geometry and representation of the model, printer characteristics and others. This demands a fine adjustment of this parameter before the definitive printing of a part once this parameter relates to the dimensional accuracy and final finish of the part. For the XY printing direction, temperature variations can change the material's structure and make it less resistant. For printing in the Z direction, the fragility of the bond between the layers is the preponderant factor. Even if the temperature changes the material's natural characteristics, the Tensile at Break value will not be defined by this change. As for Layer Height, the relationship between tensile strength and this parameter is small. We can see in TABLE IV that for an EW of 0.48mm (1.2 x the nozzle diameter), the measured variation of the bond width is on the order of 0.03 (6%).

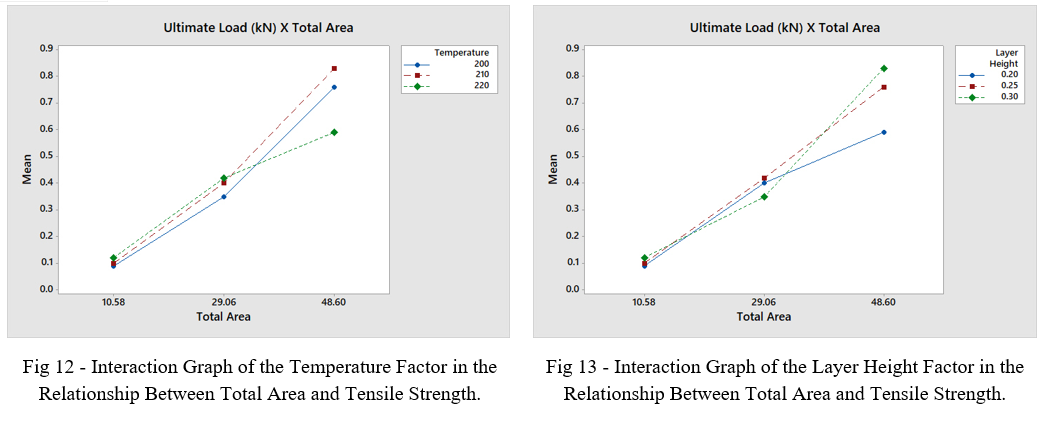
However, even so, some relationship exists between the tensile strength, extrusion temperature and layer height, as can be seen in the Interaction Graphs provided by the analysis of the Taguchi Method. These graphs show the interaction between the factors. If the graphs are not parallel, it implies that the interaction between two factors depends on the third one.

The Interaction Graph in Fig 12 shows that the relationship between tensile strength and total area does not depend on the temperature factor for small and intermediate total area values, but for larger contact areas, the greatest tensile strength is obtained for a temperature of 210 °C. The Interaction Graph in Fig 13 shows that the relationship between tensile strength and total area does not depend on the layer height factor for small and intermediate values of the total area, but for larger total areas, the greatest tensile strength is obtained for layer thickness of 0.3mm.

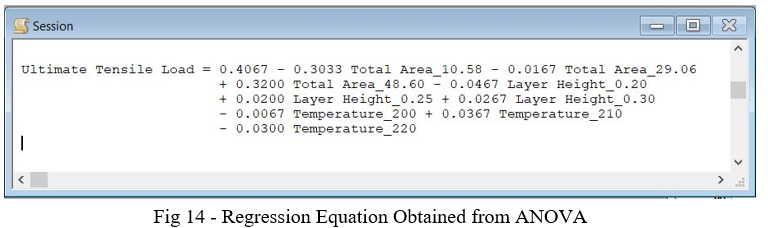
ANOVA provides a regression equation for a General Linear Model that relates Tensile to the combination of the three factors and the three levels of each factor. This equation is shown in Fig 14. However, this equation does not characterize a general equation as a function of the three factors studied. A more general equation will be presented later. Before that, let's look at the mechanics of rupture.

C. Interlayer Bond

Unlike a uniform and solid specimen, in a 3D-printed specimen the points of greatest Stress during the tensile test are concentrated at the interface between the layers (Fig 15). In the tests carried out with our specimens, with an extensometer of 22.2mm of opening, the elongation measured at the breaking point for the layer with a height of 0.2mm was, on average, 0.13mm, and for the layer of 0.3mm in height was on average 0.16mm which, divided by the number of layers covered by the extensometer, leads us to elongation values between the layers of 0.002mm and 0.001mm, respectively (TABLE VI).

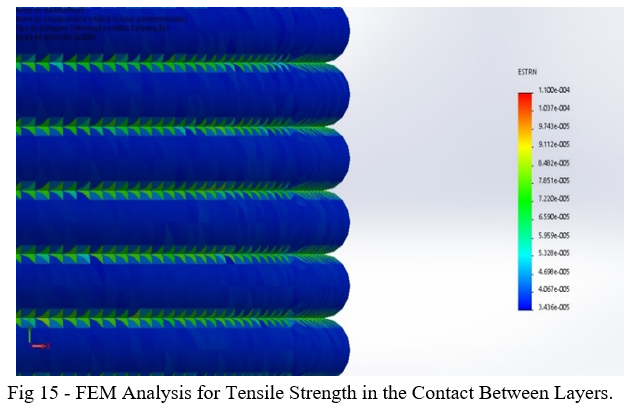
TABLE VI - Average Elongation Measured with an Extensometer in the Performed Tests.

The implication of this is that in specimens printed vertically, a very small amount of elongation is sufficient to break the bond formed during printing by diffusing heat between the layers (inter-layer fracture mode). These values are much lower than those observed in a specimen printed in the XY direction, with cross or longitudinal infill, where the elongation is very large before the rupture (in the order of 0.8 cm), which suggests a rupture of the internal structure of the polymer (in-layer fracture mode). This leads us to conclude that the tensile strength in the vertical direction of the print is mostly related to the contact area between the layers as shown by the ANOVA analysis above.

Thus, a mathematical model to determine the resistance of a part subject to traction force applied longitudinally to the layer deposition direction, would allow printing parameters to be added to the requirements from the design of a part.

D. The Ultimate Tensile Stress

A large set of additional specimens for different combinations of perimeters and infill were prepared and tested for ultimate tensile loads. The values of perimeter and infill were converted to Total Area of contact using the described methodology. Actual true Stress is calculated using the effective area of contact between the layers (Total Area). The Total Percentual Area is calculated as the percentage of the Total Area of contact to the specimen gauge area (50.27mm²). As we are using the mm² unit for the areas, the Stress in MPa is calculated by the expression:

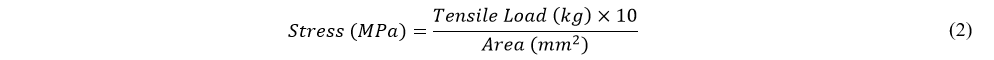
It should be noted that each of our variables, as well as the response value (Stress), have limited domains within the levels shown in

Table IIError! Reference source not found., and now for the new parameter Total Percentual Area we have 0-100%. The Maximum Stress value given by this equation must not exceed the Maximum Break Stress value obtained for specimens with 100% infill.

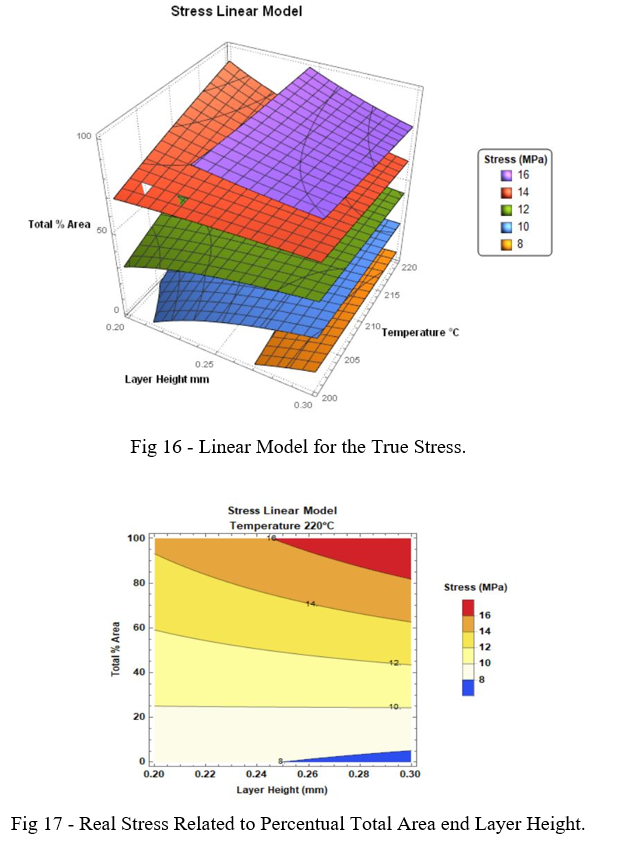
The graph in Fig 16 shows the True Stress values as a function of the studied parameters.

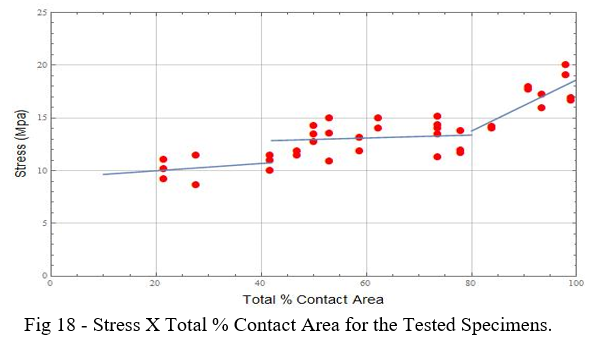
Considering the fact that the Temperature parameter has a small influence on Tensile strength, we can simplify the analysis using a 2D contour plot like the one in Fig 17. This graph allows us to establish the values to be sliced to obtain a given tensile strength in a part.

E. The Stress as a function of Total Percent Area

When we analyze the behavior between the Stress X Total % Contact Area (Fig 18), we can notice that the result differs significantly from the expected for uniform specimens. Stress value does not show up as a constant value.

We can see in this graph that the Stress is distributed in different domains of the Total % Contact Area. For small values of Total % Contact Area (this is predominantly due to the perimeters, as the infill still has little influence on the contact area), the Stress has an approximately constant value, with a small rise as the filling area increases. For intermediate Total % Contact Area values (when the contact area of infill rods competes with the perimeters) the Stress lies at a more constant value as expected for uniform specimens.

For higher Total % Contact Area values (when the infill percentage is above 90%) the Stress value increases linearly with a high rate. This is due to the fact that for high filling percentages, the extruded plastic forms a compacted mass that occupies the entire filling area, eliminating the “air gaps” and increasing the contact area beyond what is predicted by the Wb alone. This is more accentuated when we have only one perimeter because not even the “air gap” between the perimeters exists. In this situation, we have the highest tensile strength for the specimens, resulting in the maximum stress supported by PLA in the direction of bedding of the layers, this value being around 18Mpa.

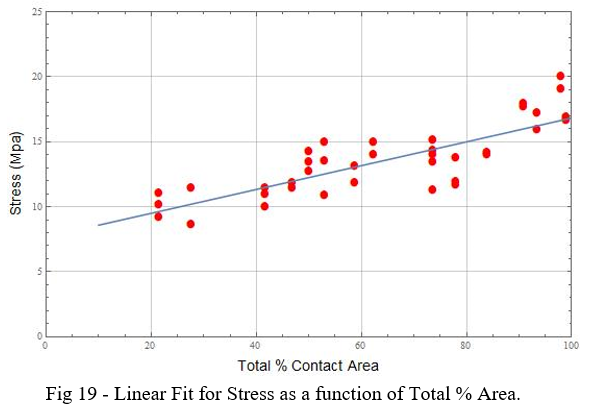
A single linear fit obtained with the values plotted in Fig 18 leads us to equation (3) and is shown in Fig 19. The regression coefficient of this fit is 0.71.

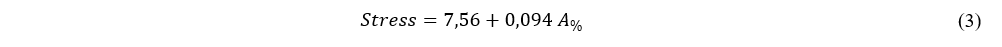
where A% stand for Total % Contact Area and for a maximum Stress value to PLA of 18Mpa.

When we design a part to be manufactured using conventional processes we have in mind the tensile load that the part must support. If the part has a specific geometry, the choice of a homogeneous and solid material is a function of the Ultimate Stress the material can support. For example, choosing whether the part will be made of plastic, aluminum, steel or another material only depends on the Stress that the material can withstand. Parts manufactured on a 3D printer given the anisotropic nature due to the bedding process and the fact that the parts are normally hollow must have a different approach. The question is what are the minimum values of slicing parameters that must be used in the part printing to obtain the necessary strength.

Equation (3) can be used to answer this question. It can be rewritten as:

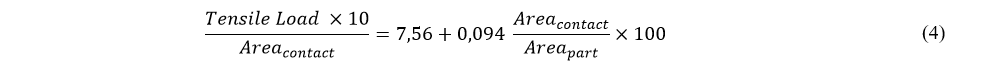
with Tensile Load in kg and areas in mm². Or, simplifying the nomenclature,

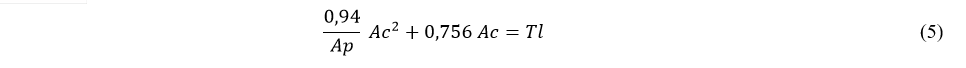
By knowing the projected area of a part and the maximum traction required, we can solve the above equation to know what contact area is necessary to be obtained when slicing the part. Considering the EW value and the length of the wire deposited in the layer (which can be obtained in the slicer software or in the resulting gcode file) we can adjust the values of perimeter and infill parameters.

However, due to what was exposed above about the Stress behavior for different intervals of the Total % Contact Area values, we suggest an expression more adherent to this variation using a third-degree polynomial regression, shown in equation (4.8), with a regression coefficient of 0.74 and shown in Fig 20.

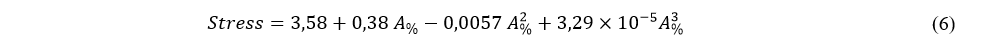
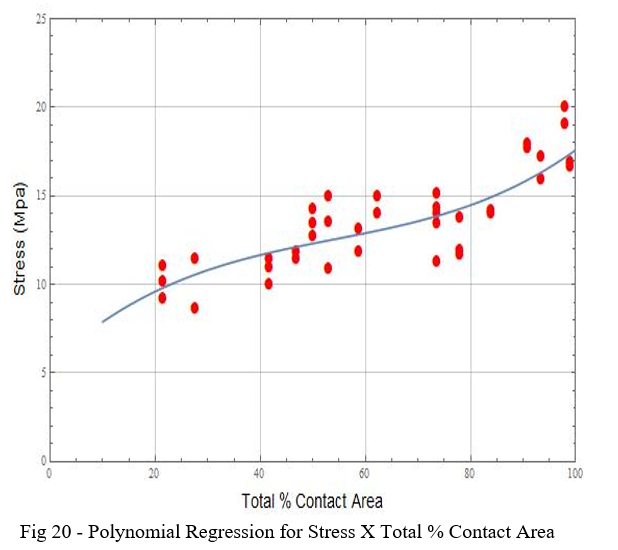
Solving equation (6) for a tensile load of 50 kg, we obtain for our specimens (gauge area of 50.27 mm²) a contact area value of 36.4 mm², which differs only 1.9% from the average real measured value for sample DBCC-F70P1C03G0T220 broken with this load.

Conclusion

To determine a mathematical model for the mechanical resistance between the layers of parts produced by FDM, the use of the total contact area between the layers proved to be more suitable than the use of non-analog properties such as number of perimeters, and relative properties such as percentage of filling. The methods developed during the research allowed this value to be easily obtained despite not being (yet) present in the slicer programs. Mathematical relationships were determined for the resistance between the layers of parts produced in PLA in FDM 3D printers as a function of the contact area between the layers. These relationships allow that the project of a part to be printed in PLA predict and add property values peculiar to FDM technology prior to the preparation of print files generated by slicer software. Two equations were presented, one linear and other polynomial. The latter better predicts the relationship between ultimate stress and contact area since it was observed that this stress has different values when analyzed as a function of the percentual area.

References

[1] M. Lay, N. L. N. Thajudin, Z. A. A. Hamid, A. Rusli, M. K. Abdullah, and R. K. Shuib, “Comparison of physical and mechanical properties of PLA, ABS and nylon 6 fabricated using fused deposition modeling and injection molding,” Compos. Part B Eng., vol. 176, no. August, p. 107341, 2019, doi: 10.1016/j.compositesb.2019.107341. [2] C. Ziemian, M. Sharma, and S. Ziemi, “Anisotropic Mechanical Properties of ABS Parts Fabricated by Fused Deposition Modelling,” in Mechanical Engineering, 2012. [3] J. F. Rodríguez, J. P. Thomas, and J. E. Renaud, “Mechanical behavior of acrylonitrile butadiene styrene (ABS) fused deposition materials . Experimental investigation Âguez,” vol. 7, no. 3, pp. 148–158, 2006. [4] S. Ahn, M. Montero, D. Odell, S. Roundy, and P. K. Wright, “Anisotropic material properties of fused deposition modeling ABS,” Rapid Prototyp. J., vol. 8, no. 4, pp. 248–257, 2002, doi: 10.1108/13552540210441166. [5] A. K. Sood, R. K. Ohdar, and S. S. Mahapatra, “Parametric appraisal of mechanical property of fused deposition modelling processed parts,” Mater. Des., vol. 31, no. 1, pp. 287–295, 2010, doi: 10.1016/j.matdes.2009.06.016. [6] J. Lee and A. Huang, “Fatigue analysis of FDM materials,” Rapid Prototyp. J., vol. 19, no. 4, pp. 291–299, 2013, doi: 10.1108/13552541311323290. [7] L. Li, Q. Sun, C. Bellehumeur, and P. Gu, “Composite modeling and analysis for fabrication of FDM prototypes with locally controlled properties,” J. Manuf. Process., vol. 4, no. 2, pp. 129–141, 2002, doi: 10.1016/S1526-6125(02)70139-4. [8] G. C. Onwubolu and F. Rayegani, “Characterization and Optimization of Mechanical Properties of ABS Parts Manufactured by the Fused Deposition Modelling Process,” Int. J. Manuf. Eng., vol. 2014, pp. 1–13, 2014, doi: 10.1155/2014/598531. [9] F. Górski, R. Wichniarek, W. Kuczko, P. Zawadzki, and P. Bu?, “Strength of Abs Parts Produced By Fused Deposition Modelling Technology – a Critical Orientation Problem,” Adv. Sci. Technol. Res. J., vol. 9, no. 26, pp. 12–19, 2015, doi: 10.12913/22998624/2359. [10] A. Lanzotti, M. Grasso, G. Staiano, and M. Martorelli, “The impact of process parameters on mechanical properties of parts fabricated in PLA with an open-source 3-D printer,” Rapid Prototyp. J., vol. 21, no. 5, pp. 604–617, 2015, doi: 10.1108/RPJ-09-2014-0135. [11] A. N. Pathan, “Influence of the FDM 3D Printing Process Parameters on In-Layer and the Inter-Layer Fracture under Tensile Failure,” Int. J. Res. Appl. Sci. Eng. Technol., vol. 8, no. 12, pp. 215–222, 2020, doi: 10.22214/ijraset.2020.32446. [12] M. Montero, S. Roundy, and D. Odell, “Material characterization of fused deposition modeling (FDM) ABS by designed experiments,” Proc. Rapid Prototyp. Manuf. Conf., pp. 1–21, 2001, doi: 26. [13] K. L. Alvarez C., R. F. Lagos C., and M. Aizpun, “Investigating the influence of infill percentage on the mechanical properties of fused deposition modelled ABS parts,” Ing. e Investig., vol. 36, no. 3, pp. 110–116, 2016, doi: 10.15446/ing.investig.v36n3.56610. [14] M. Fernandez-Vicente, W. Calle, S. Ferrandiz, and A. Conejero, “Effect of Infill Parameters on Tensile Mechanical Behavior in Desktop 3D Printing,” 3D Print. Addit. Manuf., vol. 3, no. 3, pp. 183–192, 2016, doi: 10.1089/3dp.2015.0036. [15] J. Santhakumar, U. M. Mohammed Iqbal, and M. Prakash, “Investigation on the effect of tensile strength on fdm build parts using taguchi-grey relational based multi-response optimization,” Int. J. Mech. Eng. Technol., vol. 8, no. 12, pp. 53–60, 2017. [16] J. Torres, M. Cole, A. Owji, Z. DeMastry, and A. P. Gordon, “An approach for mechanical property optimization of fused deposition modeling with polylactic acid via design of experiments,” Rapid Prototyp. J., vol. 22, no. 2, pp. 387–404, 2016, doi: 10.1108/RPJ-07-2014-0083. [17] J. J. Laureto and J. M. Pearce, “Anisotropic mechanical property variance between ASTM D638-14 type i and type iv fused filament fabricated specimens,” Polym. Test., vol. 68, no. March, pp. 294–301, 2018, doi: 10.1016/j.polymertesting.2018.04.029. [18] S. Attoye, E. Malekipour, and H. El-Mounayri, “Correlation between process parameters and mechanical properties in parts printed by the fused deposition modeling process,” Conf. Proc. Soc. Exp. Mech. Ser., vol. 8, pp. 35–41, 2019, doi: 10.1007/978-3-319-95083-9_8. [19] ASTM-D634-14, “ASTM D638-14 - Standard test method for tensile properties of plastics,” ASTM Int., vol. 08, pp. 46–58, 2016, doi: 10.1520/D0638-14.1. [20] A. A. Cavalcante, N. B. Oliveira, and I. M. Pepe, “A New Specimen Geometry for Evaluation of the Mechanical Orthotropic Properties Presented in Parts Printed by FDM,” IJRASET, vol. 9, no. December, 2021, doi: https://doi.org/10.22214/ijraset.2021.39553. [21] C. Sabino, L. Santana, I. Pereira, R. A. Paggi, and D. C. Lencina, “Avaliação de corpos de prova produzidos em pla por manufatura aditiva por extrusão e moldagem por injeção,” 13o Congr. Ibero-americano Eng. Mecânica, pp. 23–26, 2017. [22] X. Gao, S. Qi, X. Kuang, Y. Su, J. Li, and D. Wang, “Fused filament fabrication of polymer materials: A review of interlayer bond,” Addit. Manuf., vol. 37, no. 2, p. 101658, 2020, doi: 10.1016/j.addma.2020.101658. [23] M. Malviya and K. A. Desai, “Build orientation optimization for strength enhancement of fdm parts using machine learning based algorithm,” Comput. Aided. Des. Appl., vol. 17, no. 4, pp. 783–796, 2020, doi: 10.14733/cadaps.2020.783-796. [24] H. Gonabadi, A. Yadav, and S. J. Bull, “The effect of processing parameters on the mechanical characteristics of PLA produced by a 3D FFF printer,” Int. J. Adv. Manuf. Technol., vol. 111, no. 3–4, pp. 695–709, 2020, doi: 10.1007/s00170-020-06138-4. [25] T. J. Coogan and D. O. Kazmer, “Modeling of interlayer contact and contact pressure during fused filament fabrication,” J. Rheol. (N. Y. N. Y)., vol. 63, no. 4, pp. 655–672, 2019, doi: 10.1122/1.5093033. [26] S. A. Tronvoll, T. Welo, and C. W. Elverum, “The effects of voids on structural properties of fused deposition modelled parts: a probabilistic approach,” Int. J. Adv. Manuf. Technol., vol. 97, no. 9–12, pp. 3607–3618, 2018, doi: 10.1007/s00170-018-2148-x. [27] National Institutes of Health, “ImageJ - Image Processing and Analysis Software.” https://www.ittvis.com/envi/%0Ahttps://imagej.nih.gov/ij/index.html (accessed Feb. 03, 2021). [28] A. A. Cavalcante, N. B. Oliveira, J. A. M. Alfonzo, M. V. E. Lima, and I. M. Pepe, “LOW COST TENSILE TESTING MACHINE FOR FDM PARTS MECHANICAL BEHAVIOR CARACTERIZATION,” in ABCM International Congress of Mechanical Engineering, 2017, [Online]. Available: http://www.sistema.abcm.org.br/articleFiles/download/9030. [29] T. Nancharaiah, D. R. Raju, and V. R. Raju, “An experimental investigation on surface quality and dimensional accuracy of FDM components,” Int. J. Emerg. Technol., vol. 1, no. 2, pp. 106–11, 2010. [30] B. H. Lee, J. Abdullah, and Z. A. Khan, “Optimization of rapid prototyping parameters for production of flexible ABS object,” J. Mater. Process. Technol., vol. 169, no. 1, pp. 54–61, 2005, doi: 10.1016/j.jmatprotec.2005.02.259. [31] Minitab, “Interpretar os principais resultados para ANOVA para um fator,” [Recuperado: 8-setembro-2021], 2018. https://support.minitab.com/pt-br/minitab/18/help-and-how-to/modeling-statistics/anova/how-to/one-way-anova/interpret-the-results/key-results/.

Copyright

Copyright © 2022 Alexandre A. Cavalcante, Newton B. Oliveira, Jose A. M. Alfonzo, Iuri M. Pepe. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.