Link Prediction on N-ary Relational Data Based on Relatedness Evaluation

Abstract

The recent proliferation of high-resolution Earth observation data, along with the advent of open-data initiatives, has led to the availability of petabyte-scale Earth observation datasets accessible for free. However, this abundance of big data presents significant challenges for regional to global spatio-temporal analysis. The traditional approach of \"download-preprocess-store-analyze\" introduces excessive data downloading overhead and computational barriers, hindering efficient analysis. The Earth observation data cube (EODC) paradigm offers a solution by revolutionizing the storage and management of spatio-temporal RS data. Yet, the presence of multiple EODC solutions has resulted in \"information silos,\" making the sharing and joint use of RS data across EODCs difficult. To tackle these challenges, we propose a novel method of in-memory distributed data cube autodiscovery and retrieval across clouds. Our approach involves constructing a distributed in-memory data orchestration system that shields the heterogeneity of EODC storage solutions, effectively overcoming the \"information silos\" problem. Additionally, we introduce a \"larger-sites-first\" and spatio-temporal aware RS data discovery strategy that automatically identifies and retrieves data across clouds based on specific requirements. Leveraging the data cube paradigm, our article presents a \"quality-first\" data filtering strategy, enabling users to extract high-quality data relevant to their target spatio-temporal range from the vast amount of available data. This method ensures efficient data cube joint retrieval and utilization across cloud platforms.Through comparative experiments, we have demonstrated the effectiveness and efficiency of our proposed approach. By addressing the complexities of RS data management and promoting seamless data sharing across cloud-based EODCs, our method opens up new possibilities for collaborative spatio-temporal analysis, empowering researchers and organizations to make informed decisions and gain valuable insights from the vast Earth observation data resources.

Introduction

I. INTRODUCTION

The Since Google's introduction of the Knowledge Graph (KG) in 2012, KGs have gained significant popularity. Link prediction within KGs has garnered considerable attention as well, given its potential to enhance KG completion and support applications built on KGs. In the typical representation, a KG is composed of triples structured as (head entity, relation, tail entity). This representation breaks down n-ary relational facts into multiple triples using virtual entities, such as Compound Value Type (CVT) entities in Freebase [1]. Notably, n-ary relational facts are quite prevalent, with more than a third of Freebase entities participating in such relationships [2].The existing KGs, when converted into the binary triple form, have paved the way for the development of various link prediction techniques [3], [4], [5]. These methods encompass tasks like predicting head entities, relations, and tail entities. However, the conversion of n-ary relational facts into triples presents certain limitations. Firstly, it requires considering a multitude of triples during link prediction on n-ary relational data. Common link prediction methods for triples, as mentioned earlier, tend to focus on individual triples, making it complex to predict links involving multiple triples simultaneously. Secondly, the conversion process may result in a loss of structural information, which could lead to less accurate predictions. Thirdly, the introduction of virtual entities and the associated triples adds more parameters that need to be learned, magnifying the challenge of dealing with data sparsity.

In essence, while KGs and link prediction methods have made significant strides, there are still challenges to address when transforming n-ary relational facts into triples. These challenges include predicting links involving multiple triples, preserving structural information, and handling the increased complexity and data sparsity introduced by virtual entities and their corresponding triples Taking these considerations into account, this paper adopts a distinct approach where each n-ary relational fact is represented as a collection of role and role-value pairs, abbreviated as r:v pairs. This is in contrast to the conventional practice of converting such facts into multiple triples.

This novel representation avoids the introduction of additional entities and triples, ensuring that all crucial structural information is preserved. Subsequently, a method is proposed to address the challenge of link prediction on n-ary relational data, specifically aimed at predicting missing role/role-value pairs within an n-ary relational fact. Recent research has also explored link prediction for n-ary relational data. In the context of m-TransH [2], an n-ary relation is defined by mapping a sequence of roles to their corresponding role-values. Each unique mapping constitutes an n-ary relational fact. A translation-based approach is then introduced to model these facts. Building upon this, RAE [6] enhances m-TransH by incorporating the likelihood estimation of role-values co-participating in a common n-ary relational fact. However, RAE falls short in explicitly considering the roles when evaluating this likelihood.In reality, the relatedness between two role-values significantly varies based on different sequences of roles, which correspond to distinct relations. For instance, utilizing examples from Wikidata [1], consider the role sequence (person, award, point in time, together with). Under this sequence, Marie Curie and Henri Becquerel are more closely related due to their shared Nobel Prize in Physics in 1903. On the other hand, under the role sequence (person, spouse, start time, end time, place of marriage), their relatedness is less significant since they are associated with a different context. To overcome these issues, our proposed method explicitly models the interelatedness of r:v pairs within an n-ary relational fact. The necessity of this approach is illustrated by the aforementioned example. Newly introduced methods [7], [8], [9], [10] also delve into addressing these challenges. They incorporate techniques such as position-specific convolution [7], tensor decomposition [8], and structure-aware methodologies [9], [10]. However, it's noteworthy that these methods don't take type constraints into account, which our approach seeks to rectify.

II. OBJECTIVES

1. Enhanced Prediction Accuracy: The main goal is to improve the accuracy of link prediction in n-ary relational data. By explicitly considering the relatedness between role-value pairs within an n-ary relational fact, the proposed approach aims to provide more accurate predictions of missing role/role-value pairs. This should lead to better-informed decisions in various applications reliant on knowledge graphs.
2. In-Memory Data-Cube Implementation: Retained Structural Information: Unlike the conversion of n-ary relational facts into triples, the proposed method preserves the complete structural information of the original data. This ensures that the rich contextual relationships between role-value pairs are maintained, which can lead to more meaningful predictions and a deeper understanding of the data.
3. Distributed Data Discovery: Facilitating distributed data discovery across multiple cloud platforms will enable seamless collaboration among researchers and organizations. This collaborative environment will foster knowledge exchange and encourage innovative approaches to remote sensing data analysis.
4. Consideration of Role Specificity: The method aims to account for the varying significance of role-value relatedness under different sequences of roles. This takes into consideration the semantic differences and context shifts associated with distinct relations, ultimately leading to more contextually relevant predictions.

III. LIMITATIONS

The approach of Link Prediction on N-ary Relational Data Based on Relatedness Evaluation brings forward innovative strategies for improving the accuracy and contextual understanding of link predictions within complex knowledge graphs. However, it's important to recognize its limitations in achieving these goals. One significant limitation lies in its potential computational complexity. The explicit modeling of relatedness between role-value pairs in n-ary relational facts might introduce substantial computational demands, particularly as the knowledge graph scales. This could lead to longer processing times and increased resource requirements, limiting its practicality for large-scale graphs.Furthermore, the effectiveness of the approach could be compromised by data sparsity. In instances where n-ary relational facts are scarce, the method might struggle to accurately learn the relatedness patterns, resulting in less reliable predictions, especially for relations that occur infrequently. Additionally, while the incorporation of type constraints enhances prediction accuracy, it simultaneously introduces complexity. Navigating relationships between different entity types and roles can be intricate and might pose challenges during implementation.

IV. LITERATURE SURVEY

The paper by Bollacker et al. (2008) [1] presents "Freebase: A collaboratively created graph database for structuring human knowledge." In this work, the authors introduce Freebase, a significant precursor to the concept of knowledge graphs, as a collaborative and structured graph database for organizing human knowledge.

They outline the methodology and principles behind Freebase's construction, emphasizing its use of n-ary relational data representation to capture complex relationships between entities. The paper highlights the importance of incorporating diverse data sources, community contributions, and semantic relationships to build a comprehensive and interconnected knowledge repository. By introducing the concept of a structured graph database, the authors pave the way for subsequent developments in knowledge representation, link prediction, and related fields.

In [2] their paper "On the representation and embedding of knowledge bases beyond binary relations" (2016), Wen et al. delve into the representation and embedding of knowledge bases that extend beyond binary relations. The authors address the limitations of binary relations in capturing the complexities of real-world knowledge and propose an approach to incorporate higher-arity relationships. They introduce the concept of hyperrelations and a novel tensor-based model that captures these relationships effectively. Through experimentation, the authors demonstrate the advantages of their approach in capturing rich semantic information within knowledge bases. Their work contributes to advancing the representation and embedding techniques for knowledge bases, opening avenues for more accurate and comprehensive knowledge modeling beyond simple binary relationships.

In [3] their paper "A review of relational machine learning for knowledge graphs" (2016), Nickel et al. provide a comprehensive review of the landscape of relational machine learning techniques as applied to knowledge graphs. The authors outline the challenges and opportunities inherent in learning from structured data, emphasizing the importance of capturing complex relationships within knowledge graphs. They analyze various methodologies such as tensor factorization, probabilistic graphical models, and embedding-based techniques, discussing their strengths and limitations in tackling tasks like link prediction and entity classification. The paper offers valuable insights into the advancements and trends in the intersection of machine learning and knowledge graph research, facilitating a deeper understanding of effective techniques for mining information from structured data sources

1. The paper "Knowledge graph embedding: A survey of approaches and applications" by Wang et al. (2017) offers a comprehensive survey of the landscape of knowledge graph embedding techniques and their applications. The authors systematically review a wide range of embedding methods, categorizing them into translation-based, factorization-based, neural network-based, and hybrid approaches. They delve into the theoretical foundations of each category and discuss the strengths and weaknesses of various methods, highlighting their effectiveness in addressing tasks such as link prediction, entity classification, and relation discovery within knowledge graphs. The paper provides insights into the evolution of knowledge graph embedding research, serving as a valuable resource for both researchers and practitioners seeking to navigate the diverse approaches and applications in this rapidly evolving field.

In [5] the paper titled "A comprehensive survey of graph embedding: Problems, techniques, and applications" by Cai et al. (2018), the authors present an extensive survey that encompasses a wide spectrum of graph embedding techniques, their associated challenges, and diverse applications. The paper systematically categorizes graph embedding methods into local, global, and hybrid methods, addressing the nuances of graph structure, node attributes, and application domains. The authors thoroughly explore the problems and intricacies involved in graph embedding, such as preserving structural properties and handling various types of graphs. They analyze the techniques' effectiveness in addressing various applications, including node classification, link prediction, and recommendation systems. By offering a holistic view of graph embedding research, the paper serves as a valuable resource for researchers and practitioners seeking to navigate the complexities and potentials of this evolving field.

The paper [6] by Zhang et al. titled "Scalable instance reconstruction in knowledge bases via relatedness affiliated embedding" (2018) introduces an innovative approach to scalable instance reconstruction within knowledge bases using relatedness affiliated embedding. The authors address the challenge of knowledge base completion by proposing a method that leverages relatedness among entities for embedding instance information. They emphasize a focus on scalable reconstruction while capturing complex relationships. By exploiting relationships and relatedness patterns, the authors aim to enhance the quality of instance reconstruction, especially in scenarios involving large knowledge bases. The paper contributes to advancing techniques for knowledge base completion and extends the scope of embedding methods to address the challenges of scalability and complexity in real-world knowledge graph scenarios.

In [7] the paper "Knowledge hypergraphs: Extending knowledge graphs beyond binary relations" (2020) authored by Fatemi et al., the authors explore the concept of knowledge hypergraphs as an extension of traditional knowledge graphs to accommodate more complex relationships beyond binary associations. Recogniz9999ing the limitations of binary relations in capturing the intricacies of real-world data, the authors propose a hypergraph-based approach to model knowledge. By introducing hyperedges that connect multiple entities, the paper aims to capture higher-arity relationships and interdependencies more effectively. The authors highlight the advantages of this extension in enhancing the representation and reasoning capabilities of knowledge graphs.

This work contributes to the evolution of knowledge graph representation, demonstrating the potential of hypergraphs to capture and utilize more nuanced relationships for a deeper understanding of complex data domains.

The paper [8] authored by Liu et al. titled "Generalizing tensor decomposition for n-ary relational knowledge bases" (2020) presents a significant advancement in the realm of knowledge base representation by extending tensor decomposition methods to accommodate n-ary relational data. The authors address the limitations of traditional tensor decomposition approaches, which are tailored for binary relations, and propose a novel method capable of handling higher-arity relationships. By introducing a generalized tensor decomposition framework, the paper aims to capture the complexities of n-ary relations while preserving the rich semantic structure of knowledge bases. The authors demonstrate the effectiveness of their approach through experiments and analysis, showcasing its potential for enhanced link prediction and representation learning in knowledge graphs with non-binary relationships. This contribution expands the applicability of tensor decomposition techniques, offering a valuable avenue for capturing and leveraging n-ary relational knowledge more effectively.

The paper [9] authored by Rosso et al. titled "Beyond triplets: Hyper-relational knowledge graph embedding for link prediction" (2020) contributes to the advancement of link prediction in knowledge graphs by introducing a hyper-relational embedding approach that extends beyond traditional triplets. Acknowledging the limitations of triplet-based methods in capturing complex relationships, the authors propose a hyper-relational embedding framework that enables the modeling of higher-order relationships and hyperedges. By incorporating these hyper-relational patterns, the paper aims to enhance the accuracy and contextuality of link prediction. Through empirical evaluations, the authors showcase the effectiveness of their approach in capturing more nuanced relationships and providing improved predictions. This work offers a novel perspective on knowledge graph embedding, expanding the potential of embedding techniques to address the complexities of hyper-relational data in knowledge graphs.

The paper [10] authored by Guan et al. titled "Neuinfer: Knowledge inference on n-ary facts" (2020) introduces Neuinfer, a novel method designed to address the challenge of knowledge inference on n-ary relational facts. Acknowledging the complexities posed by n-ary relationships in knowledge graphs, the authors propose a neural network-based approach for inferring missing facts and relationships. Neuinfer leverages entity embeddings and structured neural networks to effectively capture and predict n-ary relations. Through extensive experimentation and analysis, the authors demonstrate the performance and efficiency of Neuinfer in inferring n-ary facts. This paper contributes to the expanding landscape of knowledge graph inference methods, offering a neural network-driven solution tailored to the unique challenges of n-ary relational data in knowledge graphs..

V. DESIGN AND IMPLEMENT

A .The Framework of NaLP

We present NaLP, a novel approach for link prediction in n-ary relational data. This method is developed based on two fundamental considerations. Firstly, we acknowledge the strong interconnection between a role and its corresponding role-value, which implies a natural binding between them. Secondly, as outlined in Section 3, our primary objective is to assess the validity of an n-ary relational fact—a collection of role-value pairs. Essentially, we aim to determine whether a given set of role-value pairs can collectively form a legitimate n-ary relational fact.

Our reasoning stems from the observation that in a valid relational fact, all the role-value pairs are closely interconnected. Thus, we hypothesize that if all role-value pairs within a set are closely related to each other, then there exists a high likelihood that these pairs can collectively constitute a valid n-ary relational fact. Guided by these principles, we formulate the NaLP framework, as depicted in the upper portion of Figure 1. This framework comprises two pivotal components: the embedding of role-value pairs (denoted as r:v pairs) and an evaluation of their relatedness. These components work in tandem to generate an evaluation score for the input fact.

For clarity, the diagram in the figure illustrates the concept using the n-ary relational fact labeled as Rel. To elaborate further, we delve into the specifics of the learning process. The role-values within the set VRel are retrieved from embedding matrices MR ∈ R|R|×k (containing role embeddings) and MV ∈ R|V |×k (containing role-value embeddings). Here, R signifies the complete set of roles within the dataset, V represents the complete set of role-values, and k indicates the dimensionality of the embeddings. For consistency, we denote the embeddings using boldface letters.

In the subsequent sections, we delve into the details of this learning process, exemplifying how NaLP functions to predict links within n-ary relational data. This approach harnesses the inherent relationships between role-value pairs to effectively evaluate the potential validity of n-ary relational facts.

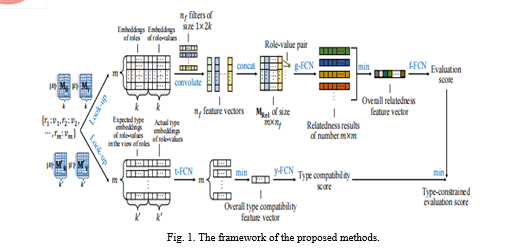
B. The R:V Pair Embedding Component

This component is designed to acquire embeddings for the given r:v pairs. This process encompasses two distinct sub-steps: feature learning of the r:v pairs (leveraging convolution as it is a robust technique for feature extraction) and the derivation of the embedding matrix for the r:v pairs. These correspond to the actions denoted as "convolute" and "concat" in the upper section of Figure 1, respectively.

C. Feature Learning of the R:V Pairs

As depicted in Figure 1, prior to the convolution step, we combine the embeddings of the roles (ri) and their corresponding role-values (vi) for each pair in the relational fact Rel. This concatenation results in the formation of a matrix with dimensions m × 2k, where each row corresponds to an individual r:v pair. Subsequently, this concatenated matrix is fed into the convolution process, utilizing a filter set ? composed of nf filters.

To ensure compatibility with the dimensions of the concatenated embeddings of the r:v pairs (which are 1 × 2k in size), we configure the filters' dimensions to match, specifically setting them as 1 × 2k. This design choice facilitates the extraction of features pertaining to the role-value pairs. Following the convolution, we obtain nf outcomes, each having a dimension of m. To enhance these outcomes, we apply the Rectified Linear Units (ReLU) function [48], resulting in nf distinct feature vectors.

D. The Embedding Matrix of the R:V Pairs

We proceed by consolidating the nf feature vectors, resulting in the creation of a matrix with dimensions m × nf. This matrix effectively embodies the embeddings of the m r:v pairs, with each row representing the embedding of an individual r:v pair. Within a row, each entry encodes the feature specific to that dimension. To formalize this, we define the embedding matrix MRel ∈ Rm×nf for the r:v pairs in the relational fact Rel:

MRel = Υ(concat(RRel, VRel) ∗ ?),

Here, Υ signifies the ReLU function, expressed as Υ(x) = max(0, x); ∗ represents the convolution operation; and concat(RRel, VRel) corresponds to the previously explained process of embedding concatenation for the r:v pairs before convolution. This formulation encapsulates the combined effect of convolution and ReLU activation, leading to the generation of the embedding matrix MRel.

E. The Principle of Relatedness Evaluation

The core principle delves into determining the feasibility of a collection of r:v pairs to collectively form a valid n-ary relational fact. As elaborated in Section 4.1, this task boils down to gauging the overarching relatedness among all the r:v pairs within the set. However, quantifying the overall relatedness within a set comprising more than two objects becomes intricate. This complexity is accentuated when dealing with sets that encompass a high arity, representing a large number of objects.

In contrast, computing the relatedness between two individual objects is comparatively straightforward. As such, the challenge lies in extrapolating the intricate overall relatedness from the simpler pairwise relatedness between the r:v pairs. To address this, we take a logical approach. If all the r:v pairs collectively form a closely-knit set—a valid n-ary relational fact—then it logically follows that any two pairs within the set are inherently highly related. This implies that the relatedness feature vector values, which measure relatedness from diverse perspectives, for any pair should be significantly substantial.

Consequently, in order to capture this relationship, we perform an element-wise minimization operation across the relatedness feature vectors for every pair of r:v pairs. This operation allows us to approximate the comprehensive relatedness feature vector for the entire set of r:v pairs. This strategy is grounded in the notion that if the relatedness feature values for each dimension are all relatively large across all pairs, the set is likely to constitute a valid n-ary relational fact.

This insight drives the design of the relatedness evaluation component. It involves estimating the relatedness between the r:v pairs and determining the aggregate relatedness of the entire set before computing the final evaluation score.

F. Relatedness Evaluation Between the R:V Pairs

The relatedness between the r:v pairs is captured through the utilization of a Fully Connected Network (FCN) accompanied by ReLU activation. Notably, the FCN is a well-established model renowned for its efficacy in discerning relationships between objects, and it has achieved remarkable performance in the realm of computer vision [45], [47]. Within this particular sub-process, it has been empirically determined that a one-layer FCN yields highly satisfactory outcomes. As a result, our approach solely employs a single fully connected layer. To delve into the specifics, the embeddings of any two r:v pairs are first concatenated. This merged vector is then passed through a fully connected layer housing ngFCN nodes. The outcome of this operation produces a vector recognized as the relatedness feature vector. In this vector, each dimension corresponds to the relatedness between the two input r:v pairs from a particular perspective.

G. The Characteristics of NaLP

It's important to distinguish the handling of input data in different methods like m-TransH [2], RAE [6], HypE [7], and GETD [8]. In these methods, all relations, accompanied by their associated role sequences, are pre-defined. Consequently, the models receive instances of these relations as inputs—specifically, sequences consisting of ordered role-values. Given that the i-th role-value of an input instance corresponds to the i-th role of its relation, altering the sequence order of input role-values is typically not permitted. This constraint stems from the fact that the positional arrangement of input role-values has a direct bearing on these methods.

Contrastingly, the proposed NaLP method takes a distinct approach. Each input to NaLP corresponds to a set of r:v pairs, representing an n-ary relational fact. This implies that the order of objects within each input holds significance for methods such as m-TransH, RAE, HypE, and GETD. However, for NaLP, the order of the r:v pairs within the input has no impact on its functioning. NaLP operates as a permutation-invariant model with regard to the input order of these r:v pairs. This property enables NaLP to effectively accommodate facts with varying arities, making it more versatile in handling a wider range of relational data.

H. The Training Process

The initialization of bgFCN and bfFCN involves setting their values to zero (Line 3). The training process of NaLP unfolds in Lines 5-21, iterating until the validation set performance reaches convergence. In each epoch, d|T0 |/βe batches of training facts are drawn from each training group T0. The training procedure for NaLP is outlined in Algorithm 1. Prior to commencement, the training set is partitioned into distinct groups, each preserving facts with similar arities (Line 1). To ensure a progressive learning approach, where NaLP gains mastery over fundamental low-arity facts before tackling higher arities, these groups are sorted based on their arities in ascending order (Line 2). Analogous procedures are applied to train the model on single-length path queries followed by all path queries [50]. Subsequently, the embedding matrices MR and MV are initialized using random values drawn from a uniform distribution between −√1k and √1k. The initializer for the filters in ? employs a truncated normal distribution with a mean of 0.0 and a standard deviation of 0.1 [40]. The initial values of WgFCN and WfFCN are set using the Xavier initializer [51]. Here, d·e refers to the ceiling function. For each chosen training fact, similar to the negative sampling method employed in TransE [20], one of its role-values is randomly replaced by a role value associated with the corresponding role, with a probability of |V|/(|V| + |R|). Alternatively, one of its roles is replaced by a random role with a probability of |R|/(|V| + |R|), thereby creating a negative sample not present in the dataset (Line 8). Following this, for each sampled n-ary relational fact or its negative counterpart Rel, the embeddings of its roles and role-values are retrieved from MR and MV, respectively (Lines 11 and 12). These embeddings are then input into the r:v pair analysis process.

I. The Training Process of NaLP.

1. Input: Training set T, role set R, role-value set V, maximum number of epochs nepoch, embedding dimension k, batch size β, number of filters nf in ?, hyperparameter ngFCN for WgFCN.
2. Output: MR and MV embeddings, along with NaLP's parameters.

a. Group facts in T based on their arities, store in T0.

b. Arrange groups in T0 by arity in ascending order.

c. Initialize MR and MV using uniform distribution between -√1k and √1k. Initialize ? with truncated normal distribution (mean=0.0, std=0.1). Initialize WgFCN and WfFCN using Xavier initializer. Initialize bgFCN and bfFCN as zeros.

d. Repeat until validation set result converges:

e. For each group T0 in T:

f. For j = 1 to floor(|T0| / β):

g. S+ ← sample β training facts from T0.

h. S- ← generate β negative samples from S+.

i. Initialize loss as 0.

j. For each Rel in (S+ ∪ S-):

k. RRel ← Look up embedding MR for roles in Rel

l. VRel ← Look up embedding MV for role-values in Rel.

m. Calculate MRel using Equation (1).

n. Compute overall relatedness feature vector RRel using Equation (2).

o. Calculate evaluation score s0(Rel) using Equation (3).

p. Compute loss L(Rel) using Equation (6).

q. Increment loss by L(Rel).

r. Update embeddings of roles and role-values in S+∪S-, filters in ?, WgFCN, WfFCN, bgFCN, and bfFCN using 5 times the loss.

s. End For

t. End For

u. Until validation set result converges.

J.  NaLP+ and tNaLP+

Both NaLP and tNaLP employ a conventional negative sampling method, akin to that found in TransE [20]. However, this approach, effective for binary relational datasets, proves less suitable for n-ary relational datasets. In reality, this method primarily pushes the model to differentiate a valid element from the remaining elements within the dataset. Unfortunately, it falls short in encouraging the model to discern r:v pairs within distinct n-ary relational facts from those in other facts.

Consequently, this paper introduces a more reasonable negative sampling mechanism that accounts for distinguishing between n-ary relational facts. This mechanism operates as follows for each n-ary relational fact with arity m:

Choose whether to randomly replace a role-value/role or r:v pair(s). If opting for role-value/role replacement, proceed to Step 2; otherwise, move to Step 3. Randomly replace one of the role-values or roles within the fact, adhering to the procedure detailed in Section 4.5.2. Determine a random number nneg ∈ (0, m) of r:v pairs to replace. Select nneg r:v pairs randomly from the training set; these r:v pairs may originate from different facts. Use these chosen r:v pairs to replace the nneg random r:v pairs within the given fact. This enhanced negative sampling mechanism extends NaLP and tNaLP to NaLP+ and tNaLP+, respectively. It's worth noting that the element-wise minimizing function used in overall type compatibility evaluation is permutation-equivariant. Moreover, the proposed improved negative sampling mechanism solely influences the negative sampling process. As a result, tNaLP, NaLP+, and tNaLP+ remain permutation-invariant with regard to the input order of r:v pairs, enabling them to proficiently manage facts of varying arities.

VI. EXPERIMENTS

A. Datasets

We performed experiments on two distinct datasets. The first dataset is JF17K4, a publicly available n-ary relational dataset. This dataset is derived from the well-known KG Freebase [1]. In JF17K4, all facts adhere to predefined standard role sequences, and their corresponding role-values are known and existing.

However, this isn't representative of all real-world scenarios. To address this, we curated a more practically applicable dataset named WikiPeople, which serves as the second dataset in our experiments. The construction of WikiPeople involves the following steps:

We began by downloading the Wikidata dump5 and extracting facts specifically related to entities categorized as human.

These extracted facts underwent further denoising. For instance, facts containing elements linked to images were filtered out. Similarly, facts containing elements categorized as {unknown value, no values} were discarded.

Next, we identified subsets of elements with a minimum of 30 mentions. The facts associated with these selected elements were retained. Each fact was parsed to form a set of its corresponding r:v pairs.

The remaining facts were randomly divided into three sets: a training set, a validation set, and a test set, distributed according to an 80%:10%:10% ratio.

By following this approach, we created the WikiPeople dataset, which reflects a more practical and realistic representation of relational data compared to JF17K4.

B. Metrics and Experimental Settings

In terms of evaluation metrics, we employ the well-established Mean Reciprocal Rank (MRR) and Hits@N. These metrics are computed similarly to those used for binary relational datasets [20]. For each test fact, one of its roles/role-values is removed and replaced with all the other roles/role-values in the sets R/V. By introducing these corrupted facts alongside the original test fact, the proposed methods generate (type-constrained) evaluation scores. These scores are then arranged in descending order, based on which the rank of the test fact is determined. This process is repeated for all other roles/role-values associated with the test fact. Consequently, MRR is calculated as the average of the reciprocal ranks, while Hits@N is the percentage of ranks that are less than or equal to N. We opt not to use the traditional mean rank (average of ranks) as a metric due to its sensitivity to outliers [53]. In both MRR and Hits@N, higher values denote superior performance. During the testing process, corrupted facts that could potentially be valid (i.e., existing in the training/validation/test set) are excluded before sorting the facts.

For the reported results of the proposed methods, we present outcomes achieved using the best combination of hyper-parameters, as determined through grid search on the validation set. The ranges for grid search are as follows, referencing ConvKB [40]: embedding dimension k ∈ {50, 100}, batch size β ∈ {128, 256}, learning rate λ ∈ {5e−6, 1e−5, 5e−5, 1e−4, 5e−4, 1e−3}, number of convolution filters nf ∈ {50, 100, 200, 400, 500}, hyper-parameter ngFCN for WgFCN ∈ {50, 100, 200, 400, 500, 800, 1000, 1200}, type embedding dimension k0 ∈ {5, 10, 20, 30, 40}, and hyper-parameter ntFCN for WtFCN ∈ {5, 10, 20, 40, 50, 80, 100, 150, 200}. These ranges cover a comprehensive exploration of hyper-parameter settings.

C. The Effectiveness of tNaLP, NaLP+, and tNaLP+

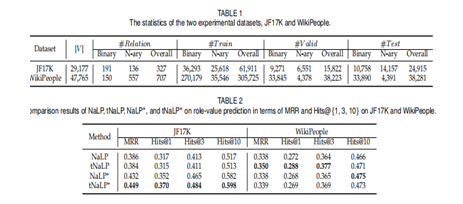
This section is dedicated to the evaluation of the extended methods, aimed at selecting appropriate techniques to compare with the baseline methods in the subsequent section. Given that role prediction is considerably simpler due to the relatively smaller role set, our focus shifts to the more challenging task of role-value prediction. The decision-making process is based on this more intricate prediction task. The experimental outcomes are presented in Table 2.

For the JF17K dataset, tNaLP+ demonstrates a noteworthy performance improvement over NaLP. Specifically, tNaLP+ outperforms NaLP by margins of 0.063, 5.3%, 7.1%, and 8.1% in terms of MRR and Hits@{1, 3, 10}, respectively. This outcome affirms the efficacy of integrating type constraints in an unsupervised manner and validates the innovation of the newly proposed negative sampling mechanism. This mechanism, which replaces a varying number of r:v pairs, not only encourages the differentiation of valid elements from other elements but also enhances the capability of NaLP+ and tNaLP+ to distinguish r:v pairs within n-ary relational facts, ultimately leading to substantially improved performance.

Turning to the WikiPeople dataset, tNaLP exhibits superior performance compared to NaLP, highlighting the importance of incorporating type constraints. Although these constraints are introduced in an unsupervised manner, their impact is evident. However, when considering the results of NaLP+ and tNaLP+ on WikiPeople, it's notable that the newly introduced negative sampling mechanism doesn't yield the same level of effectiveness. This discrepancy could be attributed to the higher proportion of binary relational facts in the WikiPeople dataset. To verify this theory, a new dataset, WikiPeople-n, is derived from WikiPeople. This new dataset maintains all n-ary relational facts while randomly eliminating certain binary relational facts to attain the same binary-to-n-ary ratio as the training set of JF17K. The results of experiments on WikiPeople-n are summarized in Table 3. These results reveal that NaLP+ and tNaLP+ significantly outperform NaLP and tNaLP, respectively, thereby validating the earlier conjecture. However, the overall performance on WikiPeople-n remains lower than that observed for JF17K and WikiPeople. Given that WikiPeople simulates real-world complexities, including data incompleteness, insertion, and updates, its practicality and challenges are more pronounced than those of JF17K. With the removal of numerous binary relational facts in WikiPeople-n, these complexities intensify, rendering WikiPeople-n a more demanding dataset than JF17K and WikiPeople.

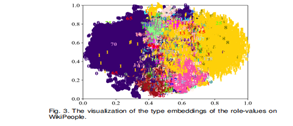
Notably, tNaLP doesn't exhibit significant performance enhancements compared to NaLP across all datasets, particularly on JF17K and WikiPeople-50bi. To delve into the reasons behind these observations, we conducted an analysis focusing on type information. The following analysis on WikiPeople applies similarly to other datasets.

We visually represented the type embeddings of role-values on WikiPeople in Figure 3. Here, role-values sharing the same type are denoted by the same label and color. For dimension reduction of type embeddings, we employed t-SNE [54]. Moreover, the statistical breakdown of role-value types on WikiPeople (logarithmic scale) is depicted in Figure 4. The x-axis signifies the role-value type size (ntype), i.e., the number of role-values within that type, while the y-axis represents the number of types having a given ntype.

Although tNaLP's type embeddings capture valuable information (Figure 3), wherein role-values of the same type are positioned closely, the dataset's type distribution is severely imbalanced (Figure 4). Consequently, tNaLP fails to manifest its superiority. This type distribution imbalance is even more pronounced on JF17K and WikiPeople-50bi, leading to tNaLP's notably inferior performance on these datasets.

In summary, based on the observations from Tables 2, 3, and 4, we deduce that the new negative sampling mechanism yields favorable outcomes on datasets with numerous n-ary relational facts. Conversely, when dealing with datasets featuring a more balanced type distribution, introducing type constraints emerges as the preferred approach.

D. Link Prediction Performance Comparison on N-ary Relational Data

1. Baselines

Notably, tNaLP doesn't exhibit significant performance enhancements compared to NaLP across all datasets, particularly on JF17K and WikiPeople-50bi. To delve into the reasons behind these observations, we conducted an analysis focusing on type information. The following analysis on WikiPeople applies similarly to other datasets.

We visually represented the type embeddings of role-values on WikiPeople in Figure 3. Here, role-values sharing the same type are denoted by the same label and color. For dimension reduction of type embeddings, we employed t-SNE [54]. Moreover, the statistical breakdown of role-value types on WikiPeople (logarithmic scale) is depicted in Figure 4. The x-axis signifies the role-value type size (ntype), i.e., the number of role-values within that type, while the y-axis represents the number of types having a given ntype. Although tNaLP's type embeddings capture valuable information (Figure 3), wherein role-values of the same type are positioned closely, the dataset's type distribution is severely imbalanced (Figure 4). Consequently, tNaLP fails to manifest its superiority. This type distribution imbalance is even more pronounced on JF17K and WikiPeople-50bi, leading to tNaLP's notably inferior performance on these datasets. In summary, based on the observations from Tables 2, 3, and 4, we deduce that the new negative sampling mechanism yields favorable outcomes on datasets with numerous n-ary relational facts. Conversely, when dealing with datasets featuring a more balanced type distribution, introducing type constraints emerges as the preferred approach.

2. Experimental Results

Analyzing the results, it's evident that both tNaLP and tNaLP+ outperform the baseline methods. This underscores the effectiveness of considering r:v pair relatedness, introducing type constraints, and proposing a more reasonable negative sampling mechanism. Impressively, compared to the best-performing baseline HypE, tNaLP and tNaLP+ exhibit improvements of 14.0% and 12.1% on Hits@1, respectively. This outcome illustrates that the proposed methods excel at accurately identifying valid role-values.

Notably, RAE performs substantially worse than the other methods. This observation aligns with expectations, as tNaLP and tNaLP+ are better equipped to handle diverse and complex data. They elegantly manage issues like data incompleteness, insertion, and updates that are pervasive in WikiPeople. In contrast, RAE and HypE define new relations, which could result in data sparsity when instances of these new relations are limited. Despite HypE benefiting from position-specific convolution, its performance still lags behind the proposed methods. To provide a more comprehensive evaluation of tNaLP and tNaLP+ for role-value prediction, we select the best-performing baseline from Table 6, namely HypE, and furnish detailed experimental results for each arity (>2) in Table 7 (arities with less than 10 facts are not reported). Observing the outcomes in Table 7, it's evident that the proposed methods consistently hold an advantage across various arities.

E. Overall Relatedness Analysis

In the proposed methods, the overall relatedness feature vector of a set of r:v pairs, i.e., an n-ary relational fact, is the crucial intermediate result. We conduct further analyses to dig deep into what it has learned. 6.5.1 Distinguishability Metric According to Section 4.1, a valid n-ary relational fact is expected to have an overall relatedness feature vector of large values, while an invalid n-ary relational fact is on the contrary. How to evaluate the degree of largeness? Actually, the relative magnitude between a valid n-ary relational fact and its corrupted facts is relatively more meaningful. Specifically, it is expected that a valid n-ary relational fact has larger values in a majority of dimensions of the overall relatedness feature vector compared to its corrupted facts, and thus the valid n-ary relational fact is distinguishable from its corrupted facts. Therefore, we propose the follow[1]ing metric to measure this type of distinguishability: d(Rel+, Rel-) = sum (sgn(RRel+ − RRel-)) − sum (sgn(RRel- − RRel+)),(10) where Rel+ is a valid n-ary relational fact, and Rel[1]is one of its corrupted facts; RRel+ and RRel- are the overall relatedness feature vectors of Rel+ and Rel-=, respectively; sgn(x) is the function that returns 1, if x > 0, otherwise, returns 0; sum(·) is the element-wise sum function. In Equa[1]tion (10), the left part of the minus sign counts the numberof dimensions that RRel+ is larger than RRel-, and the right part is defined similarly. Hence, d(Rel+, Rel-) measures the relative amount that RRel+ has more dimensions of larger values than RRel-.

F. Ablation Study

To thoroughly examine the rationale behind the design choices outlined in Section 4, we conducted an ablation study on NaLP. To ensure the robustness of our findings, these experiments were conducted using the WikiPeople dataset, specifically focusing on the more challenging task of role-value prediction. In this ablation study, we made alterations to the NaLP model to assess the impact of different components. Specifically, within the r:v pair embedding component, we substituted the convolution operation with addition and multiplication operations, denoted as NaLP(plus) and NaLP(mul) respectively.

Additionally, in the relatedness evaluation component, where element-wise minimizing was originally employed, we replaced it with element-wise maximizing and calculating the mean, referred to as NaLP(emax) and NaLP(emean) respectively.

The results of the experimental comparison between the NaLP model and the various ablation methods are presented in Table 9. The observations drawn from the table are noteworthy. It becomes evident that the NaLP model consistently outperforms all the ablation methods by a significant margin.

This strongly suggests that convolution is a markedly superior approach for feature learning compared to addition and multiplication. Furthermore, our experimental findings indicate that element-wise minimizing is a more effective choice when compared to element-wise maximizing and the mean operation.

In summary, the ablation study reinforces the robustness and effectiveness of the original NaLP design choices. The superiority of convolution and element-wise minimizing is reaffirmed by the substantial performance differences observed across these experimental configurations. In summary, the ablation study reinforces the robustness and effectiveness of the original NaLP design choices. The superiority of convolution and element-wise minimizing is reaffirmed by the substantial performance differences observed across these experimental configurations.

G. Complexity Analysis

To assess the efficiency of our proposed methods, we conducted a comparative analysis against representative and state-of-the-art link prediction techniques on n-ary relational data. Our evaluation criteria included measuring the Floating Point Operations (FLOPs) and parameter sizes, focusing on the larger WikiPeople dataset.

In our comparison, we excluded the GETD method [8] due to its requirement for all facts to possess the same arities, which is not a realistic assumption. Consequently, we omitted this method from our assessment.

Upon examining the results in Figure 6, a few key observations can be made. Notably, the NaLP model and tNaLP+ exhibit similar FLOPs, positioning them within a comparable efficiency range. Although these models entail more FLOPs compared to RAE [6], HINGE [9], and NeuInfer [10], they are substantially less time-intensive than HypE [7].

Turning our attention to the parameter sizes, it's evident that all the methods under consideration exceed a parameter count of 5,000M. In this context, our proposed methods align closely with NeuInfer in terms of parameter sizes, demonstrating a favorable balance. Furthermore, when contrasted with HypE and HINGE, our proposed methods present significantly smaller parameter footprints.

In summary, the evaluation of efficiency showcases the competitive nature of our proposed methods. NaLP and tNaLP+ demonstrate a favorable trade-off between FLOPs and time consumption, showcasing efficiency similar to RAE, HINGE, and NeuInfer. Moreover, our methods exhibit parameter sizes that are on par with NeuInfer and notably smaller than HypE and HINGE.

VII. FUTURE WORK

In the context of role-value prediction, our proposed methods, tNaLP and tNaLP+, exhibit remarkable performance improvements compared to the current state-of-the-art approach. Specifically, they demonstrate enhancements of up to 14.0% and 12.1% in Hits@1 accuracy, respectively. Looking ahead to future research directions, we plan to explore the integration of more expressive neural network models. This exploration aims to better capture favorable features for evaluating relatedness, potentially leading to even more effective link prediction results. Furthermore, our current work focuses solely on utilizing facts present in the datasets for n-ary relational data link prediction. In the future, we aim to introduce additional sources of information, such as rules and external text data, to further enhance the capabilities of the proposed methods. Additionally, our approach involving type constraints for roles and role-values, alongside the introduction of a more reasonable negative sampling mechanism, could potentially be applied to boost the performance of other state-of-the-art link prediction techniques designed for n-ary relational data. Notably, this enhancement strategy could be extended to recently published methods like NeuInfer [10].

In summary, our future endeavors will delve into the exploration of more sophisticated neural network models and the incorporation of supplementary information sources. We also anticipate applying the insights gained from this study to refine existing state-of-the-art methods and contribute to advancing the field of link prediction in n-ary relational data.

Conclusion

This paper introduces a novel approach for handling link prediction in n-ary relational data, where each fact is represented as a set of r:v pairs. We present the NaLP framework and its extensions, which are specifically designed to address the challenges associated with n-ary relational data. The design of these methods incorporates two important characteristics: permutation invariance to accommodate variations in the order of r:v pairs, and the ability to effectively handle facts with varying arities. By assessing the relatedness between all pairs of r:v pairs within an n-ary relational fact, NaLP can approximate the overall relatedness of the entire set of r:v pairs. This aggregated relatedness information is then used to derive feature vectors that play a crucial role in determining the validity of input facts. Building upon the NaLP foundation, we introduce tNaLP, NaLP+, and tNaLP+ by integrating unsupervised type constraints for roles and role-values, a more reasonable negative sampling mechanism, and a combination of both strategies, respectively. These extensions aim to enhance the adaptability and performance of the NaLP framework. To address the scarcity of publicly available n-ary relational datasets, we contribute a practical dataset called WikiPeople. Moreover, we create derived datasets—WikiPeople-n, WikiPeople-0bi, WikiPeople-50bi, and WikiPeople-100bi—by introducing varying proportions of binary relational facts. These datasets are made accessible online to facilitate further research in this domain. The efficacy of our proposed methods is demonstrated through extensive experiments conducted on both the established JF17K dataset and our newly developed datasets. The results consistently highlight the strengths and superiority of the proposed methods, reaffirming their potential to effectively handle link prediction tasks in n-ary relational data scenarios.

References

[1] Bollacker, C. Evans, P. Paritosh, T. Sturge, and J. Taylor, “Free base: A collaboratively created graph database for structuring human knowledge,” in Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, 2008, pp. 1247–1250. [2] J. Wen, J. Li, Y. Mao, S. Chen, and R. Zhang, “On the representation and embedding of knowledge bases beyond binary relations,” in Proceedings of the 25th International Joint Conference on Artificial Intelligence, 2016, pp. 1300–1307. [3] M. Nickel, K. Murphy, V. Tresp, and E. Gabrilovich, “A review of relational machine learning for knowledge graphs,” Proceedings of the IEEE, vol. 104, no. 1, pp. 11–33, 2016. [4] Q. Wang, Z. Mao, B. Wang, and L. Guo, “Knowledge graph embedding: A survey of approaches and applications,” IEEE Transactions on Knowledge and Data Engineering, vol. 29, no. 12, pp.2724–2743, 2017. [5] H. Cai, V. W. Zheng, and K. C.-C. Chang, “A comprehensive sur vey of graph embedding: Problems, techniques, and applications,” IEEE Transactions on Knowledge and Data Engineering, vol. 30, no. 9, pp. 1616–1637, 2018. [6] R. Zhang, J. Li, J. Mei, and Y. Mao, “Scalable instance reconstruc tion in knowledge bases via relatedness affiliated embedding,” in Proceedings of the 27th International Conference on World Wide Web, 2018, pp. 1185–1194. [7] B. Fatemi, P. Taslakian, D. V´azquez, and D. Poole, “Knowledge hypergraphs: Extending knowledge graphs beyond binary rela tions,” in Proceedings of the 29th International Joint Conference on Artificial Intelligence, 2020, pp. 2191–2197. [8] Y. Liu, Q. Yao, and Y. Li, “Generalizing tensor decomposition for n-ary relational knowledge bases,” in Proceedings of the 29th International Conference on World Wide Web, 2020, pp. 1104–1114. [9] P. Rosso, D. Yang, and P. Cudr´e-Mauroux, “Beyond triplets: Hyper-relational knowledge graph embedding for link predic tion,” in Proceedings of the 29th International Conference on World Wide Web, 2020, pp. 1885–1896 [10] S. Guan, X. Jin, J. Guo, Y. Wang, and X. Cheng, “Neuinfer: Knowledge inference on n-ary facts,” in Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, 2020, pp. 6141–6151. [11] D. Vrande?ci´c and M. Kr¨otzsch, “Wikidata: A free collaborative knowledgebase,” Communications of the ACM, vol. 57, no. 10, pp. 78–85, 2014. [12] M. Nickel, V. Tresp, and H.-P. Kriegel, “A three-way model for collective learning on multi-relational data,” in Proceedings of the 28th International Conference on Machine Learning, 2011, pp. 809–816. [13] M. Nickel, X. Jiang, and V. Tresp, “Reducing the rank in relational factorization models by including observable patterns,” in Pro ceedings of the 27th International Conference on Neural Information Processing Systems, 2014, pp. 1179–1187. [14] D. Krompa?, S. Baier, and V. Tresp, “Type-constrained represen tation learning in knowledge graphs,” in Proceedings of the 14th International Conference on The Semantic Web, 2015, pp. 640–655. [15] T. Trouillon, J. Welbl, S. Riedel, E. Gaussier, and G. Bouchard, “Complex embeddings for simple link prediction,” in Proceedings of the 33rd International Conference on Machine Learning, vol. 48, 2016, pp. 2071–2080. [16] Y. Tay, A. T. Luu, S. C. Hui, and F. Brauer, “Random semantic tensor ensemble for scalable knowledge graph link prediction,” in Proceedings of the 10th ACM International Conference on Web Search and Data Mining, 2017, pp. 751–760. [17] H. Manabe, K. Hayashi, and M. Shimbo, “Data-dependent learn ing of symmetric/antisymmetric relations for knowledge base completion,” in Proceedings of the 32nd AAAI Conference on Artificial Intelligence, 2018, pp. 3754–3761. [18] B. Ding, Q. Wang, B. Wang, and L. Guo, “Improving knowledge graph embedding using simple constraints,” in Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, 2018, pp. 110–121. [19] P. Jain, P. Kumar, S. Chakrabarti et al., “Type-sensitive knowledge base inference without explicit type supervision,” in Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers). Association for Computational Linguistics, 2018, pp. 75–80. [20] A. Bordes, N. Usunier, A. Garcia-Duran, J. Weston, and O. Yakhnenko, “Translating embeddings for modeling multi relational data,” in Proceedings of the 26th International Conference on Neural Information Processing Systems, 2013, pp. 2787–2795. [21] Z. Wang, J. Zhang, J. Feng, and Z. Chen, “Knowledge graph embedding by translating on hyperplanes,” in Proceedings of the 28th AAAI Conference on Artificial Intelligence, 2014, pp. 1112–1119. [22] Y. Lin, Z. Liu, M. Sun, Y. Liu, and X. Zhu, “Learning entity and relation embeddings for knowledge graph completion,” in Proceedings of the 29th AAAI Conference on Artificial Intelligence, 2015, pp. 2181–2187. [23] G. Ji, S. He, L. Xu, K. Liu, and J. Zhao, “Knowledge graph embedding via dynamic mapping matrix,” in Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics, 2015, pp. 687–696. [24] Y. Lin, Z. Liu, H. Luan, M. Sun, S. Rao, and S. Liu, “Modeling relation paths for representation learning of knowledge bases,” in Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, 2015, pp. 705–714. [25] H. Xiao, M. Huang, and X. Zhu, “TransG: A generative model for knowledge graph embedding,” in Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics, 2016, pp. 2316–2325 [26] G. Ji, K. Liu, S. He, and J. Zhao, “Knowledge graph completion with adaptive sparse transfer matrix,” in Proceedings of the 30th AAAI Conference on Artificial Intelligence, 2016, pp. 985–991. [27] Y. Jia, Y. Wang, H. Lin, X. Jin, and X. Cheng, “Locally adaptive translation for knowledge graph embedding,” in Proceedings of the 30th AAAI Conference on Artificial Intelligence, 2016, pp. 992–998. [28] R. Xie, Z. Liu, and M. Sun, “Representation learning of knowledge graphs with hierarchical types,” in Proceedings of the 25th Interna tional Joint Conference on Artificial Intelligence, 2016, pp. 2965–2971. [29] S. Ma, J. Ding, W. Jia, K. Wang, and M. Guo, “TransT: Type based multiple embedding representations for knowledge graph completion,” in Joint European Conference on Machine Learning and Knowledge Discovery in Databases, 2017, pp. 717–733. [30] S. Guo, Q. Wang, B. Wang, L. Wang, and L. Guo, “Semantically smooth knowledge graph embedding,” in Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics (Vol ume 1: Long Papers), 2015, pp. 84–94. [31] “SSE: Semantically smooth embedding for knowledge graphs,” IEEE Transactions on Knowledge and Data Engineering, vol. 29, no. 4, pp. 884–897, 2017. [32] T. Ebisu and R. Ichise, “TorusE: Knowledge graph embedding on a Lie group,” in Proceedings of the 32nd AAAI Conference on ArtificialIntelligence, 2018, pp. 1819–1826. [33] “Generalized translation-based embedding of knowledge graph,” IEEE Transactions on Knowledge and Data Engineering, vol. 32, no. 5, pp. 941–951, 2020. [34] Y. Shen, N. Ding, H. Zheng, Y. Li, and M. Yang, “Modeling relation paths for knowledge graph completion,” IEEE Transactions on Knowledge and Data Engineering, 2020. [35] X. Dong, E. Gabrilovich, G. Heitz, W. Horn, N. Lao, K. Murphy, T. Strohmann, S. Sun, and W. Zhang, “Knowledge Vault: A web scale approach to probabilistic knowledge fusion,” in Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2014, pp. 601–610. [36] B. Shi and T. Weninger, “ProjE: Embedding projection for knowl edge graph completion,” in Proceedings of the 31st AAAI Conference on Artificial Intelligence, 2017, pp. 1236–1242. [37] M. Schlichtkrull, T. N. Kipf, P. Bloem, R. v. d. Berg, I. Titov, and M. Welling, “Modeling relational data with graph convolutional networks,” in Proceedings of the 15th Extended Semantic Web Confer ence, 2018, pp. 593–607. [38] T. Dettmers, P. Minervini, P. Stenetorp, and S. Riedel, “Convolu tional 2D knowledge graph embeddings,” in Proceedings of the 32nd AAAI Conference on Artificial Intelligence, 2018, pp. 1811–1818. [39] S. Guan, X. Jin, Y. Wang, and X. Cheng, “Shared embedding based neural networks for knowledge graph completion,” in Proceedings of the 27th ACM International Conference on Information and Knowl edge Management, 2018, pp. 247–256. [40] D. Q. Nguyen, T. D. Nguyen, D. Q. Nguyen, and D. Phung, “A novel embedding model for knowledge base completion based on convolutional neural network,” in Proceedings of the 16th Annual Conference of the North American Chapter of the Association for Com putational Linguistics: Human Language Technologies, vol. 2, 2018, pp.327–333. [41] C. Shang, Y. Tang, J. Huang, J. Bi, X. He, and B. Zhou, “End-to end structure-aware convolutional networks for knowledge base completion,” in Proceedings of the 33rd AAAI Conference on Artificial Intelligence, 2019, pp. 3060–3067. [42] Q. Zhu, X. Zhou, J. Tan, and L. Guo, “Knowledge base reasoning with convolutional-based recurrent neural networks,” IEEE Trans actions on Knowledge and Data Engineering, 2019. [43] S. Vashishth, S. Sanyal, V. Nitin, and P. Talukdar, “Composition based multi-relational graph convolutional networks,” in Proceed ings of the 8th International Conference on Learning Representations, 2020. [44] B. Yang, W.-t. Yih, X. He, J. Gao, and L. Deng, “Embedding entities and relations for learning and inference in knowledge bases,” in Proceedings of the 3rd International Conference on Learning Representations, 2015. [45] N. Guttenberg, N. Virgo, O. Witkowski, H. Aoki, and R. Kanai, “Permutation-equivariant neural networks applied to dynamics prediction,” arXiv preprint arXiv:1612.04530, 2016. [46] M. Zaheer, S. Kottur, S. Ravanbhakhsh, B. P´oczos, R. Salakhut dinov, and A. J. Smola, “Deep sets,” in Proceedings of the 31st International Conference on Neural Information Processing Systems, 2017, p. 3394–3404. [47] A. Santoro, D. Raposo, D. G. Barrett, M. Malinowski, R. Pascanu, P. Battaglia, and T. Lillicrap, “A simple neural network module for relational reasoning,” in Proceedings of the 31st Annual Conference on Neural Information Processing Systems, 2017, pp. 4967–4976. [48] V. Nair and G. E. Hinton, “Rectified linear units improve restricted boltzmann machines,” in Proceedings of the 27th International Con ference on International Conference on Machine Learning, 2010, pp. 807–814. [49] D. Kingma and J. Ba, “Adam: A method for stochastic optimiza tion,” arXiv preprint arXiv:1412.6980, 2014. [50] K. Guu, J. Miller, and P. Liang, “Traversing knowledge graphs in vector space,” in Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, 2015, pp. 318–327. [51] X. Glorot and Y. Bengio, “Understanding the difficulty of training deep feedforward neural networks,” in Proceedings of the 13rd International Conference on Artificial Intelligence and Statistics, 2010, pp. 249–256. [52] S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Proceed ings of the 32nd International Conference on Machine Learning, 2015, pp. 448–456

Copyright

Copyright © 2023 Vinay S Navale , Chetan Jane , Anvita B, Kalyan B, Satvik A. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.