Review of Literature on Self-Excited Induction Generators and Controllers

Abstract

Wind energy is one of the most important and promising sources of renewable energy all over the world. Throughout the globe, in the last, three- or four-decades generation of electricity from wind energy has created a wide interest. At the same time, there has been a rapid development of wind energy-related technology. The control and estimation of wind energy conversion systems constitute a vast subject and are more complex than those of dc drives. Induction generators are widely preferable in wind farms because of their brushless construction, robustness, low maintenance requirements, and self-protection against short circuits. Low cost, robustness, and ease of maintenance are attractive features of induction generators. With wind turbine and micro/mini-hydro generators as an alternative energy source, the induction generators are being considered as an alternative choice to well-developed synchronous generators because of their simplicity, ruggedness, little maintenance, price, brushless (in squirrel cage construction), absence of separate dc source, self-protection against severe overloads and short circuits. In isolated systems, squirrel cage induction generators with capacitor excitation, known as self-excited induction generators (SEIGs), are very popular. This paper presents a review of literature related to the present status of research work on self-excited induction generators (SEIG), their terminal voltage control strategies, and over the past years discussing the classification of induction generators, steady-state and transient analysis, voltage control aspects, and parallel operation of SEIG.

Introduction

I. INTRODUCTION

Renewable energy is generally defined as energy that is collected from resources that are naturally replenished on a human timescale, such as sunlight, wind, rain, tides, waves, and geothermal heat. One major advantage with the use of renewable energy is that as it is renewable it is therefore sustainable and so will never run out. Renewable energy facilities generally require less maintenance than traditional generators. Their fuel being derived from natural and available resources reduces the costs of operation. Even more importantly, renewable energy produces little or no waste products such as carbon dioxide or other chemical pollutants, so has minimal impact on the environment. Renewable energy projects can also bring economic benefits to many regional areas, as most projects are located away from large urban centres and suburban’s of the capital cities. These economic benefits may be from the increased use of local services as well as tourism.

Solar Energy-Photovoltaic Systems, Wind Energy, Geothermal Energy, Bio-energy, Hydropower, Ocean Energy, Hydrogen & Fuel Cells are the different types of renewable energy sources. Out of all available sources, wind energy is utilized more. Compared to other forms of renewable energy, wind power is considered very reliable and steady, as wind is consistent from year to year and does not diminish during peak hours of demand. Initially, the construction of wind farms was a costly venture. But thanks to recent improvements, wind power has begun to set peak prices in wholesale energy markets worldwide and cut into the revenues and profits of the fossil fuel industry [1]. To convert wind energy to electrical energy we require a conversion device or a machine. A machine that can convert mechanical energy to electrical energy can be used as a conversion device in wind energy systems. Permanent magnet systems or induction generators can be used in wind to electrical generation. But the high cost of permanent magnets makes permanent magnet machines excess cost and so induction generators have a cutting edge over permanent magnet machines. In wind systems, Induction generators (IG) can be of two types-singly excited induction generators (SEIG) and doubly-fed induction generators (DFIG) [2]. DFIG consists of two back-to-back converters and makes the system costlier. So SEIG is preferred more in wind conversion systems.  SEIG coupled directly to the grid has been successfully used in wind turbines for decades. Particularly in combination with the stall-controlled three-bladed wind rotors, they initially represented by far the most commonly used electrical concept. But the absorption of reactive power for its operation, SEIG needs reactive power compensation [3]. This is the main disadvantage while using induction generators.

In this research, the modeling of SEIG will be done along with the reactive power compensation. The properties of SEIG will be studied when the SEIG is integrated to the grid. The loads are of two types-linear and non-linear. There is no problem in having linear loads in the system but with the presence of non-linear loads, the system power quality reduces along with the introduction of harmonics. Thus, the presence of non-linear loads requires compensation at PCC.  Power quality is delivering uninterrupted power supply to the customers maintain power factor, voltage, and frequency within nominal values. FACTS controllers are found to be a good choice for power quality improvement. The concept of FACTS (Flexible Alternating Current Transmission System) [4-5] refers to a family of power electronics-based devices able to enhance AC system controllability and stability and to increase power transfer capability. The installation of FACTS devices (with serial or parallel connections) in a wind farm substation or in the terminals of wind turbines is increasing rapidly owing mainly to the specifications listed in the Transmission System Operators’ (TSO) grid codes which require those wind turbines should provide ancillary services similar to those of conventional synchronous generators. The self-excitation phenomenon of an induction machine is still under considerable attention although it is known for more than a half-century [13]–[23]. The self-excited induction generator (SEIG) has attracted considerable attention due to its applicability as a stand-alone generator using different conventional and non-conventional energy resources with its advantages over the conventional synchronous generator. When a standalone induction machine is driven by a mechanical prime mover, the residual magnetism in the rotor of the machine induces an EMF in the stator windings at a frequency proportional to the rotor speed. This EMF is applied to the capacitors connected to the stator terminals and causes reactive current to flow in the stator windings. Hence a magnetizing flux in the machine is established. The final value of the stator voltage is limited by the magnetic saturation within the machine. The induction machine is then capable of operating as a generator in isolated locations without a grid supply. From the circle diagram of the induction machine in the negative slip region, it is seen that the machine draws a current, which lags the voltage by more than 90. This means that real power flows out of the machine but the machine needs reactive power. To build up a voltage across the generator terminals, excitations must be provided by some means; therefore, the induction generator can work in two modes (i.e., grid-connected and isolated mode). In the case of a grid-connected mode, the grid-connected induction generator (GCIG) takes its excitation from the lines and generates real power via slip control when driven above the synchronous speed. The operation is relatively simple as voltage and frequency are governed by the grid voltage and grid frequency respectively. In the case of isolated mode, the induction generator draws reactive power by connecting a capacitor bank across the generator terminals [24]. For an isolated mode, there must be a suitable capacitor bank connected across the generator terminals. This phenomenon is known as capacitor self-excitation and the induction generator is called a “SEIG.” The process of voltage build up in an induction generator is very much similar to that of a dc generator. When the rotor of the induction generator is run, the residual magnetism present in rotor iron creates a small emf across stator terminals. This voltage causes a capacitor current to flow. The flux due to current is added with residual flux and generates a stator terminal voltage. This voltage produces a current in the capacitor bank which then generates voltage. This cumulative process continues till the intersection point between the saturated magnetization curve and capacitor load line. The intersection point gives no load generated e.m.f.at the magnetizing current. The voltage build process depends upon the capacitor value. The higher the value of capacitance, the greater is the voltage build-up. In the absence of a proper value of residual magnetism, the voltage will not build up. So it is desirable to maintain a high level of residual magnetism, as it does ease the process of machine excitation. The operating conditions resulting in demagnetization of the rotor (e.g., total collapse of voltage under resistive loads, the rapid collapse of voltage due to short circuit, etc. should be avoided).

II. MATHEMATICAL ANALYSIS AND MODELING OF SEIG SYSTEM

SEIG system consists of a squirrel cage induction motor, prime mover, excitation capacitor, and three-phase load. The layout diagram of SEIG system is shown in fig.2.1. The primary requirement for the induction machine to work as an induction generator is the excitation current to produce a rotating magnetic field. For a grid-connected machine, it takes reactive current from the grid whereas for a standalone machine reactive power is supplied locally by the help of a shunt and a series of passive elements. 

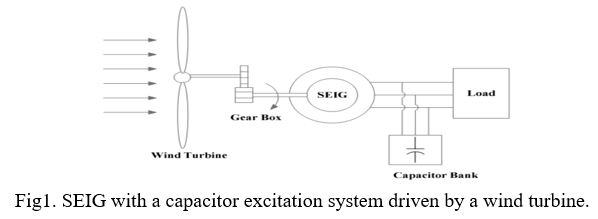
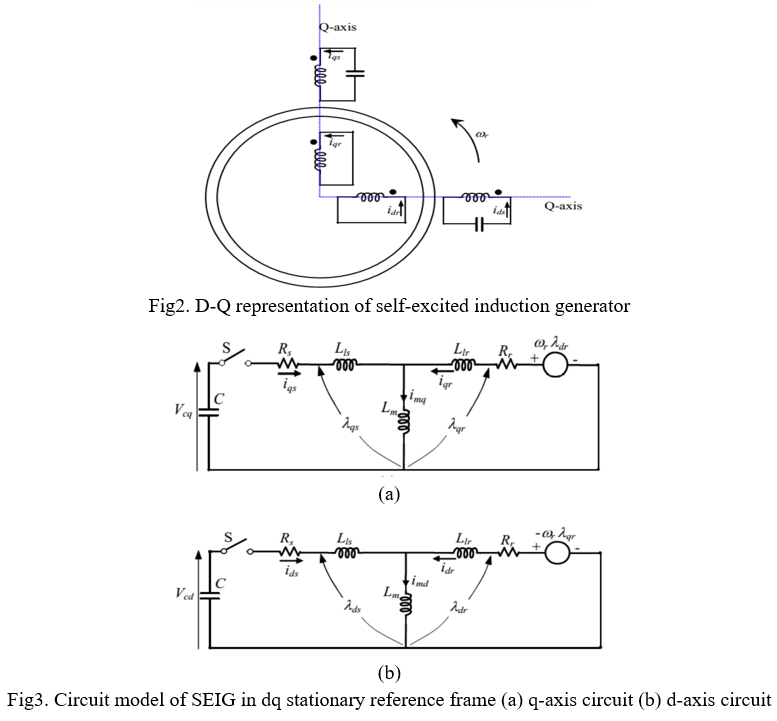
Modeling of Self-Excited Induction Generator In electrical machine analysis, a three-axis to two axes transformation is applied to produce simpler expressions that make complex systems simple to analyze and solutions easy to find. The three axes are representing the real three-phase supply system. However, the two axes are fictitious axes representing two fictitious phases, displaced by 900, to each other. Here the assumption taken is that the three-axes and the two-axes are in a stationary reference frame. It can be rephrased as a transformation between abc and stationary dq0 axes. The conventional per-phase equivalent circuit representation of an induction machine is convenient to use for steady-state analysis. However, the d-q representation is used to model the SEIG under dynamic conditions. The d-q representation of a SEIG with capacitors connected at the terminals of the stator windings and without any electrical input from the rotor side is shown in Fig. 2.2. Fig. 2.3 represents the stationary stator reference frame model in direct and quadrature axes separately.

III. MPPT MAXIMUM POWER POINT TRACKING (MPPT) CONTROL ANALYSIS

An increase in its generation capacity with the reduction of per-unit cost makes it more affordable for remote area locations; where small-scale WEGS is an attractive option. For such a stand-alone system, a self-excited induction generator (SEIG) and permanent magnet synchronous generator (PMSG) [1] are preferable wind generators (WG). Nowadays, PMSG [2] is more used as a direct drive (w/o gearbox) WG, however, SEIG [3]–[5] can be a good choice due to its low cost, ruggedness, and inherent overload protection. Further to make the system efficient, performance improvement and extraction of maximum power are major concerns. Though several articles are available on the maximum power point tracking (MPPT) algorithm [6], still further research is going on to improve the overall performance. Broadly, MPPT algorithms can be divided into two types such as speed sensor-based and speed sensor less.

Permanent magnet synchronous generator (PMSG), Self-excited induction generator (SEIG), Doubly fed induction generator (DFIG) are commonly used as wind generators in WECS. For the low power stand-alone WEGS, SEIG and PMSG are mainly used [3]–[5]. Because of lower cost, less maintenance, and inherent short circuit protection, SEIG is preferred over PMSG [6]. Transient performance and Steady-state analysis of SEIG have been well established in [7]. In order to make the efficient WEGS, a maximum power point tracking (MPPT) control strategy has been introduced for maximizing the extracted turbine power. The turbine-generated power depends on the speed of the turbine, power coefficient (Cp), and the air density which is constant. Each power-speed curve is characterized by a unique rotor speed corresponding to an optimum power for the particular wind speed. To track this MPP, several algorithms are there, such as Tip speed ratio (TSR) control, perturb and observe (P&O), power signal feedback method (PSF), fuzzy-logic based scheme, etc. [8]–[12]. In TSR control method, an anemometer is required to measure the wind speed and reference speed of the rotor corresponding to the MPP of the set wind velocity. Moreover, the system cost increases due to anemometer and for small-scale WT, TSR control is not frequently used because of the passive yaw control. [13],[14]. The speed encoders are used to implement the MPPT control strategy of WEGS. The use of this encoder involves extra space, additional cost, extra wiring, and careful mounting which reduces the robustness of systems [13], [15]–[17]. For the stand-alone system, some form of backup is almost required to maintain the reliability of the system. The battery is commonly used for backup [18]. The energy storage systems play a vital role in a stand-alone WEGS to perform both functions of storing and measuring energy at an adequate time [19]–[22].

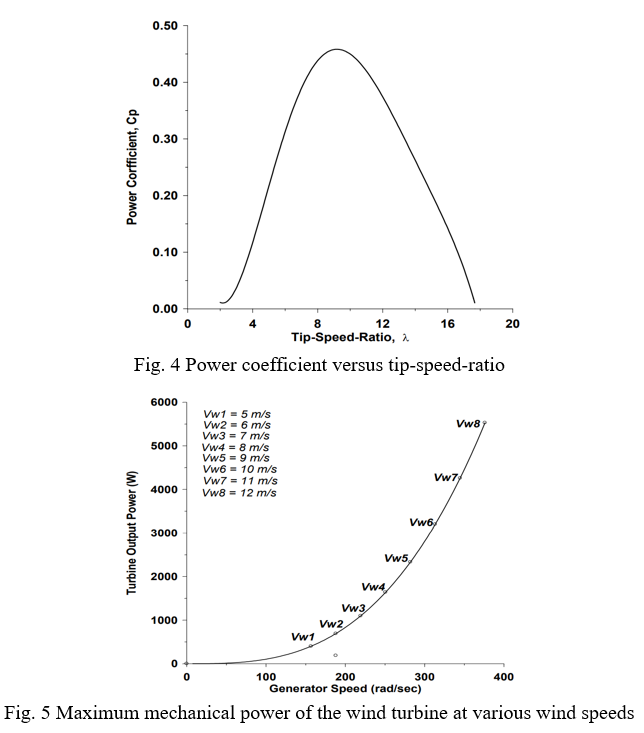
 Fig. 5 shows the optimum operating point for obtaining the maximum mechanical power versus the speed curve at various wind speeds. These optimum points correspond to the condition in which the power coefficient Cp becomes a maximum. From Fig. 4, the maximum value of the power coefficient, Cp-max equals 0.46 at the maximum tip speed ratio λmax, of about 9.2. When the generator speed is always controlled at the optimum speed given in (6), the tip-speed ratio remains the optimum value, and the maximum power point tracking (MPPT) control can be achieved. In this case, information on wind speed is required. At any wind speed, we can calculate the optimum rotational speed of the generator from (6), and then the maximum mechanical power is calculated from (9). The maximum power is used as the power refers to the grid-connected current regulated pulse width modulation (CRPWM) inverter.

IV. CONTROL STRATEGY

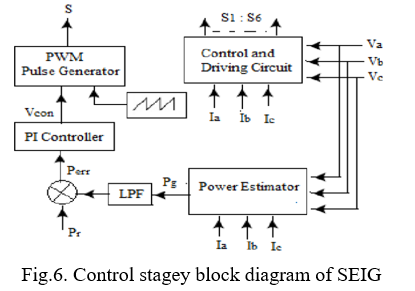
Figure 2 illustrates the block diagram of the SEIG control strategy for a stand-alone mode of operation. It is a two-loop control. The inner loop controls the SEIGs terminal voltage and frequency control in the outer loop.

A. Frequency Control

The value of the inverter AC voltage can be made constant if both the DC voltage and the modulation index do not vary. The exceeding power can be consumed by a controllable load which is a dumping resistance situated in the dc side of the PWM inverter enabling the total power supplied by the generator to match the sum between the consumer’s loads and dump load.

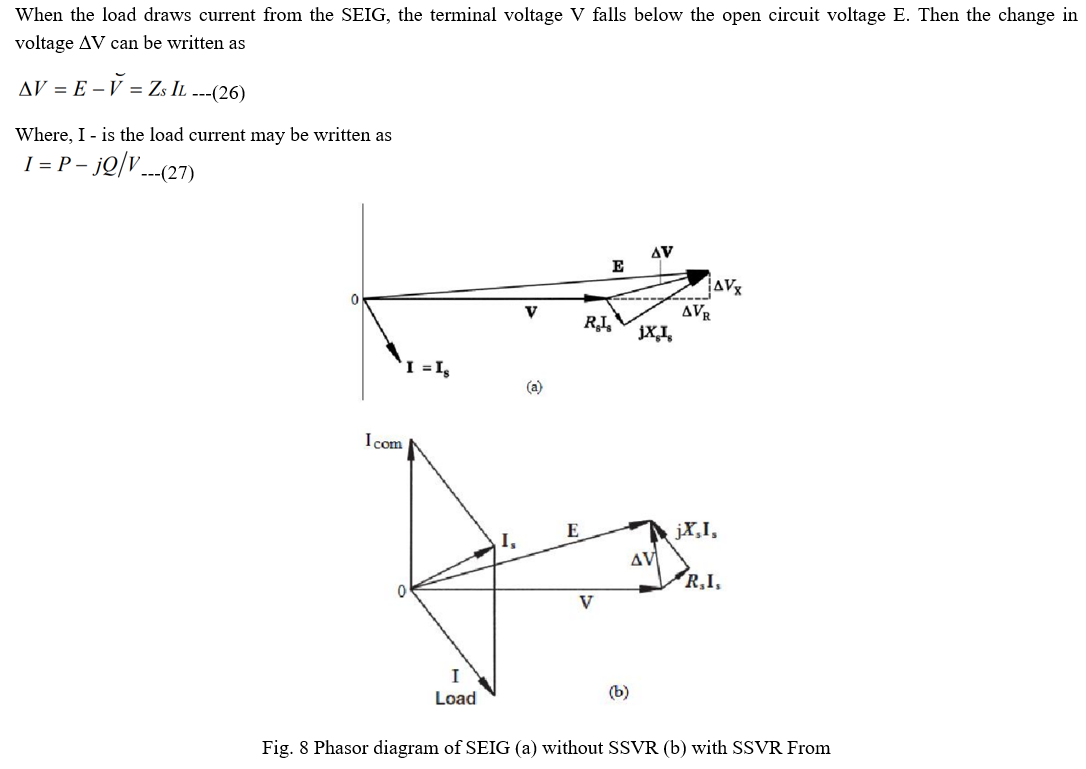
V. PERFORMANCE ANALYSIS OF SELF EXCITED INDUCTION GENERATOR

The performance analysis of self-excited induction generator can be categorized in to the following- (i) Steady state analysis (ii) transient analysis (iii) Voltage control aspect (iv) The parallel operation of SEIG.

A. Steady State Analysis

In an isolated power system, both the terminal voltage and frequency are unknown and have to be computed for a given speed, capacitance, and load impedance. Therefore both from the design and operational point of view, the steady state analysis of SEIG is of great interest. L. Sridhar[25]proposed an algorithm to predict the steady state performance of SEIG feeding an induction motor. Symmetrical components method is used to reduce the complex three-phase generator-load system to a simple equivalent passive circuit. A function minimization technique is employed to solve this equivalent circuit in order to determine the excitation frequency and magnetizing reactance. Alghuwainem [29] has examines the steady-state analysis and performance of an isolated three-phase self-excited induction generator (SEIG) driven by regulated and unregulated turbine. Abdul rahman [30] presents a steady state analysis of three phase self-excited induction generator. The problem is formulate has a multidimensional optimization problem. A constrained optimizer is used to minimize a cost function of the total impedance or admittance of the circuit of the generator to obtain the frequency and other performance of the machine. Olorunfemi Ojo [33] presents the modeling and steady-state performance of single-phase induction generators based on the principles harmonic balance including Magnetizing flux linkage saturation and flux dependent core loss resistances.

B. Transient Analysis

The transient studies of induction generators are related to voltage build up due to self-excitation and load perturbation. To investigate the SEIG transient performance under balanced condition, the D-Q model can be used. Many articles been presented on the transient/dynamic analysis of self-excited induction generator [34]-[37]. Wang [38] presents transient performance of a stand-alone self-excited induction generator (SEIG) under unbalanced excitation capacitors. An approach based on three-phase induction machine model is employed to derive dynamic equations of an isolated SEIG under unbalanced conditions The neutral points of both Y-connected excitation capacitor bank and Y-connected stator windings of the SEIG is connected together though a neutral line. In [42], the transient performance of a series-compensated three-phase self-excited induction generator (SEIG) feeding a dynamic load such as a three-phase squirrel-cage induction motor (IM) is discussed. Mathematical modeling and simulation study of SEIG and an induction motor (SEIG-IM) combination is carried out using MATLAB/Simulink. In [43], a generalized state-space dynamic model of a three phase SEIG has been developed using d-q variables in stationary reference frame for transient analysis. The proposed model for induction generator, load and excitation using state space approach can handle variable prime mover speed, and various transient conditions e.g. load perturbation, switching states etc.

C. Voltage Control Aspects

The induction machine has no field windings; therefore the current to magnetize the machine must be supplied by the system to which it is connected. Induction generator has two major drawbacks. First is the need for reactive power support and other is poor voltage regulation. Induction generators require the supply of reactive power [44].Unbalanced reactive power operation results in voltage variation. Sridhar [45] have discussed a methodology to choose the appropriate value of capacitor for desired regulation of short- shunt SEIG. The minimum capacitance requirement of SEIG is inversely proportional to the square of speed and maximum saturated magnetizing reactance. A new strategy for controlling voltage and frequency of a self-excited induction generator (SEIG) is presented in [48].An external excitation circuit, comprising permanently connected capacitors and electronically switched inductances is used. The external circuit allows compensating for the generator reactive demand. Bhim Singh [49] have Presented the design of static compensator(STATCOM)-based voltage regulator for self-excited induction generators (SEIGs). To maintain constant terminal voltage, the required adjustable reactive power can be provided by a STATCOM consisting of ac inductors, a dc bus capacitor, and solid-state self-commutating devices. A dynamic model of the SEIG–STATCOM feeding nonlinear loads using stationary d−q axes reference frame is developed for predicting the behaviour of the system under transient conditions.

D. Parallel Operation of SEIG

A stand-alone SEIG is unlikely to supply the energy demand of ordinarily growing loads for long time. Thus, multiple generators operating in parallel may be required to harvest the maximum energy available at a site. Parallel operation of induction generator has the advantages of eliminating of the need for synchronization and of the associated problem with hunting etc. The references [13]-[14] are available on the parallel operation of such units.

Wang [15] has proposed an Eigen value-based methodology to analyse the dynamic performances of parallel-operated SEIG supplying an IM load. Determination of minimum starting value of capacitance required for self-excitation is analysed. This phenomenon cannot be easily simulated using the conventional models because it has such a fast transient nature. An innovative and automatic numerical solution for steady-state and transient analysis of any number of SEIGs operating in parallel is presented [17].The effect of parameter variations on the performance of parallel-connected SEIG operating in stand-alone mode[18].Effects of parameter deviations on the power sharing, current sharing, VAR requirements, and on the voltage regulation have been examined in this paper.

VI. APPLICATIONS

In India there is a huge gap between demand and supply of electric power. Every year this gap is widening and to cope up with the increasing demand, load shedding is often resorted to. Installation of new power plants requires huge capital and land. Due to these constraints, pace of growth in generation is low. Many developing countries are facing this problem. Development on the renewable energy front is also very slow due to their pertinent issues. Small scale electrical power generation is becoming popular in many countries as it helps in reducing the cost of electricity, the stress on the main system and transmission distribution expenses to remote areas. But due to their obvious operational advantages and owing to availability of modern control techniques, induction generators are assuming significance. Induction generators employing slip ring induction motors are already in use for wind power generation in grid connected mode [35]. When an induction generator is not connected to supply grid, it is said to be operating in self-excited mode. In this mode, normally small induction motors are used, and capacitors are connected to its terminals for the supply of required reactive power. These generators can be used for wind and picot hydro generation [36].

Conclusion

A review of the SEIG is done in the above paper. The usage of the SEIG in Wind turbine systems has a vast demand nowadays. It is necessary to regulate the terminal voltage and frequency of SEIG operated in a standalone generator. Solutions to solve these problems different techniques are presented in the literature. The investigations spread over the last three decades indicate the technical and economic viability of using induction generators for electric power generation to harness renewable energy sources, particularly in remote and far-flung areas where extension of the grid is not economically feasible. The induction generator’s ability to generate power at varying speeds facilitates its application in various modes such as self-excited stand-alone (isolated) mode; in parallel with a synchronous generator to supplement the local load and in grid-connected mode. The use of SEIG compared to the synchronous generator can reduce the system cost considerably. This article has presented a comprehensive literature survey on an important aspect of SEIG such as the process of self-excitation, steady-state and transient analysis, voltage control, and parallel operation of SEIG so that further work can be carried out for better results.

References

[1] Global Wind Energy Council, Global Wind Power Statistics, 2015. (accessed on 29.04.16). [2] A.R. Sudhamshu, M.C. Pandey, N. Sunil, N.S. Satish, V. Mugundhan, R.K. Velamati, Numerical study of effect of pitch angle on performance characteristics of a HAWT, Int. J. Eng. Sci. Technol. 19 (1) (2016) 632–641. [3] H. Li, Z. Chen, Overview of different wind generator systems and their comparisons, IET Renew. Power Gener. 2 (2) (2008) 123–138. [4] P. Chauhan, J. Chatterjee, H. Bhere, B. Perumal, and D. Sarkar, “Synchronized operation of dsp-based generalized impedance controller with variable-speed isolated seig for novel voltage and frequency control,” IEEE Transactions on Industry Applications, vol. 51, no. 2, pp. 1845– 1854, 2014. [5] R. E. Raj, C. Kamalakannan, and R. Karthigaivel, “Genetic algorithmbased analysis of wind-driven parallel operated self-excited induction generators supplying isolated loads,” IET Renewable Power Generation, vol. 12, no. 4, pp. 472–483, 2017. [6] L. Wang and D.-J. Lee, “Coordination control of an ac-to-dc converter and a switched excitation capacitor bank for an autonomous self-excited induction generator in renewable-energy systems,” IEEE Transactions on Industry Applications, vol. 50, no. 4, pp. 2828–2836, 2014. [7] S. Kumar, K. Vijayakumar, and S. Neeli, “A seig-based dc nanogrid for rural electrification,” Journal of The Institution of Engineers (India): Series B, pp. 1–7, 2019. [8] M. Cucuzzella, R. Lazzari, S. Trip, S. Rosti, C. Sandroni, and A. Ferrara, “Sliding mode voltage control of boost converters in dc microgrids,” Control Engineering Practice, vol. 73, pp. 161–170, 2018. [9] A. B. K. Mukkapati, R. Kaur, K. Vijayakumar, and S. Neeli, “Voltage regulation of quadratic boost converter with fixed frequency sliding mode controller,” in 2017 IEEE International Conference on Electrical, Instrumentation and Communication Engineering (ICEICE). IEEE, 2017, pp. 1–6. [10] R. Karthigaivel, N. Kumaresan, M. Subbiah, Analysis and control of self-excited induction generator-converter systems for battery charging applications, IET Electric Power Appl. 5 (2) (2011) 247–257. [11] D. Joshi, K.S. Sandhu, M.K. Soni, Constant voltage constant frequency operation for a self-excited induction generator, IEEE Trans. Energy Convers. 21 (1) (2006) 228–234. [12] N. Ammasaigounden, M. Subbiah, Microprocessor-based voltage controller for wind-driven induction generators, IEEE Trans. Ind. Electron. 37 (6) (1990) 531–537. [13] S. Senthil Kumar, N. Kumaresan, M. Subbiah, Analysis and control of capacitorexcited induction generators connected to a micro-grid through power electronic converters, IET Gener. Transm. Distrib. 9 (10) (2015) 911–920. [14] S. Senthil Kumar, N. Kumaresan, N. Ammasai Gounden, Namani Rakesh, Analysis and control of wind-driven self-excited induction generators connected to the grid through power converters, Front Energy 6 (4) (2012) 403–412. [15] K. Nishida, T. Ahmed, M. Nakaoka, A cost-effective high-efficiency power conditioner with simple MPPT control algorithm for wind-power grid integration, IEEE Trans. Ind. Appl. 47 (2) (2011) 893–900. [16] V. Agarwal, R.K. Aggarwal, P. Patidar, C. Patki, A novel scheme for rapid tracking of maximum power point in wind energy generation systems, IEEE Trans. Energy Convers. 25 (1) (2010) 228–236. [17] Z. Chen, J.M. Guerrero, F. Blaabjerg, A review of the state of the art of power electronics for wind turbines, IEEE Trans. Power Electron. 24 (8) (2009) 1859– 1875. [18] B.C. Babu, K. Sridharan, E. Rosolowski, Z. Leonowicz, Analysis of SDFT based phase detection system for grid synchronization of distributed generation systems, Int. J. Eng. Sci. Technol. 17 (2014) 270–278. [19] Z. Chen, E. Spooner, Grid power quality with variable speed wind turbines, IEEE Trans. Energy Convers. 16 (2) (2001) 148–154. [20] N. Kumar, T.R. Chelliah, S.P. Srivastava, Analysis of doubly-fed induction machine operating at motoring mode subjected to voltage sag, Int. J. Eng. Sci. Technol. (2016), http://dx.doi.org/10.1016/j.jestch.2016.01.015. [21] K. Vijayakumar, N. Kumaresan, N. Ammasai Gounden, S.B. Tennakoon, Real and reactive power control of hybrid excited wind-driven grid-connected doubly fed induction generators, IET Power Electron. 6 (6) (2013) 1197–1208. [22] M.-S. Lu, C.-L. Chang, W.-J. Lee, L. Wang, Combining the wind power generation system with energy storage equipment, IEEE Trans. Ind. Appl. 45 (6) (2009) 2109–2115. [23] J.P. Barton, D.G. Infield, Energy storage and its use with intermittent renewable energy, IEEE Trans. Energy Convers. 19 (2) (2004) 441–448. [24] P. Wang, L. Goel, X. Liu, F.H. Choo, Harmonizing AC and DC: a hybrid AC/DC future grid solution, IEEE Power Energy Mag. 11 (3) (2013) 76–83. [25] J.J. Justo, F. Mwasilu, J. Lee, J.-W. Jung, AC-microgrids versus DC-microgrids with distributed energy resources: a review, Renew. Sustain. Energy Rev. 24 (2013) 387–405. [26] D. Das, N. Kumaresan, V. Nayanar, K. Navin Sam, N. Ammasai Gounden, Development of BLDC motor based elevator system suitable for DC microgrid, IEEE/ASME Trans. Mechatron. 21 (3) (2016) 1552–1560. [27] G. Byeon, T. Yoon, S. Oh, G. Jang, Energy management strategy of the dc distribution system in buildings using the EV service model, IEEE Trans. Power Electron. 28 (4) (2013) 1544–1554. [28] L. Xu, D. Chen, Control and operation of a DC microgrid with variable generation and energy storage, IEEE Trans. Power Del. 26 (4) (2011) 2513– 2522. [29] W. Li, X. Mou, Y. Zhou, C. Marnay, On voltage standards for DC home microgrids energized by distributed sources, in: Proceeding 7th International Power Electronics and Motion Control Conference (IPEMC’12), Harbin, China, 2012, pp. 2282–2286. [30] S. Anand, B.G. Fernandes, Optimal voltage level for DC microgrids, in: Proceeding 36th Annual Conference on IEEE Industrial Electronics Society (IECON’10), Glendale, AZ, 2010, pp. 3034–3039. [31] K. Strunz, E. Abbasi, D.N. Huu, DC microgrid for wind and solar power integration, IEEE, J. Emerg. Sel. Top. Power Electron. 2 (1) (2014) 115–126. [32] V. Nayanar, N. Kumaresan, N. Ammasai Gounden, A single sensor based MPPT controller for wind-driven induction generators supplying DC microgrid, IEEE Trans. Power Electron. 31 (2) (2016) 1161–1172. [33] Olorunfemi Ojo, Ishwar Bhat, “An analysis of single-phase self-excited induction generators:model development and steady-state calculations,”IEEE Transactions on Energy Conversion, Vol. 10, No. 2, June 1995. [34] C.S. Demoulias and P.G. Holmes, “Transient behavior and self excitation of wind driven induction generator after its disconnection from power grid,”IEEE Transaction Energy Conversion, Vol. 5, No. 2, June 1990, pp. 272-278. [35] Olorunfemi Ojo,“The transient and qualitative performance of a self-excited single-phase induction generator,” IEEE Transactions on Energy Conversion, Vol. 10, No. 3, September 1995. [36] M.H.Salama and P.G.Holme, “ Transient and steady state load performance of a stand alone self excited induction generator,” IEE Proc -Electr Power Appl, Vol 143, No I , January 1996. [37] J.M. Elder, J.T. Boys, and J.L.Woodward, “Integral cycle control of stand alone generators,”IEE Proceedings, Part C, Vol. 132, No. 2, pp. 57-66, 1985. [38] Li Wang, and Ruey Yong Deng, “Transient performance of an induction generator under balanced excitation capacitor,” IEEE Transactions on Energy Conversion, Vol. 14, No. 4, December 1999. [39] S.K. Jain, J.D. Sharma and S.P. Singh,“Transient performance of three-phase self-excitedinduction generator during balancedand unbalanced faults.” IEE Proc.-Gener. Trans. Distrib. Vol. 149, No. 1. January 2002. [40] Bhim Singh, S. S. Murthy,and Sushma Gupta “Transient Analysis of Self-Excited Induction Generator With Electronic Load Controller (ELC)Supplying Static and Dynamic Loads,” IEEE Transactions On Industry Applications, Vol. 41, No. 5, September/October 2005. [41] Bhaskara Palle, M. Godoy Simões, and Felix A. Farret, “Dynamic Simulation and Analysis of Parallel Self-Excited Induction Generators for Islanded Wind Farm Systems,” IEEE Transactions On Industry Applications, Vol. 41, No. 4, July/August 2005. [42] Bhim Singh, Madhusudan Singh, and A. K. Tandon, “Transient Performance of Series-Compensated Three-Phase Self-Excited Induction Generator Feeding Dynamic Loads,” IEEE Transactions On Industry Applications, Vol. 46, No. 4, July/August 2010. [43] Avinash Kishore, G. Satish Kumar, “Dynamic modeling and analysis of three phase self-excitedinduction generator using generalized state-space approach,” SPEEDAM 2006 International Symposium on Power Electronics, Electrical Drives, Automation and Motion. [44] E. Suarez, and G. Bortolotto, “Voltage-frequency control of a self excited induction generator,” IEEE Transaction on Energy Conversion, Vol. 12, No. 4, December 1997, pp. 62-69. [45] L. Shridhar, B. Singh, C. S. Jha, B. P. Singh, and S. S. Murthy, “Selectionof capacitors for the self regulated short shunt selfexcited generator,” IEEE Trans. Energy Convers., vol. 10, no. 1, pp. 10–17, Mar. 1995. [46] Swati Devabhaktuni, S.V. Jayram kumar , “Design of excitation capacitance for self excited induction generator,”International journal of computer science & communication Networks, Vol. 1, No.-3, pp. 191-198. [47] N. H. Malik and A. A. Mazi, “Capacitive requirements for isolated self excited induction generators,” IEEE Trans. Energy Convers., vol. EC-2,no. 1, pp. 62–69, Mar. 1987. [48] Eduardo Sukez and Gustavo Bortolotto,“Voltage-frequency control of a self excitedinduction generator,” IEEE Transactions on Energy Conversion, Vol. 14, No. 3, September 1999. [48] Bhim Singh, S. S. Murthy,and Sushma Gupta,“Analysis and Design of STATCOM-Based Voltage Regulator for Self-Excited Induction Generators,” IEEE Transactions On Energy Conversion, Vol. 19, No. 4, December 2004. [49] Bhim Singh, S. S. Murthy, and Sushma Gupta, “STATCOMBased Voltage Regulator for Self-Excited Induction Generator Feeding Nonlinear Loads,” IEEE Transactions On Industrial Electronics, Vol. 53, No. 5, October 2006.

Copyright

Copyright © 2022 S. Radha Krishna Reddy, Dr. J. B. V. Subrahmanyam, Dr. A. Srinivasula Reddy. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.