Markov Model for Analyzing Sensitivity to Change in Machine Repair Reliability Using Its Transition Probability Diagram

Abstract

Our main goal is to model the efficiency of a redundant machining system made up of a lot of machines and analyze how reliable the system is. Combining the ideas of switching failure and geometric reneging makes it possible to look at the possible outcomes in a more nuanced way. It is assumed that both the time it takes for a machine to break down and the time it takes to fix it follow an exponential distribution. A lot of performance indicators have been made so that a quantitative analysis of the machine interference problem can be done. Mean time to failure, dependability, and the rate of giving up are all examples of such efficiency measures. The evaluation of reliability indices has been shown. This shows how the values of these indices change when different system parameters are changed. This was done so that could be confirmed and a good explanation could be given.

Introduction

I. INTRODUCTION

A. Reliability Models for Machine Repair Systems

Queuing and reliability models are being used more and more to study how well multiple machining system functional processes work. Many queueing theorists and practitioners are interested in Markov modeling of machine repair systems because it lowers the overall cost of running an organization or system and improves the quality of service for customers. This is the case because the things it sells are so good. The machine repair issue is a good example of a finite population queueing system because it is useful in many different fields, from auto repair shops to the space industry. Here are a few examples of these sectors: A machining system will always have problems, but they should be fixed quickly and cheaply so that they don't have a big effect on how well the system works. As more machines are used in a system and machines break down more often, interference problems start to happen. With the rise of software-embedded machining systems, where computers are used to automate the allocation of different work processes, there has been a rise in interest in studying finite population queueing systems and the problems of machine maintenance and reliability. When individual machines in a machining system break down, it can cause a chain reaction of problems,  such as lost revenue, downtime, inefficient use of resources, and so on. We need to do more than just regular maintenance to get this problem under control. We need to set up a system of backup machines. The Automated Manufacturing System (AMS) is a good example of this idea. The AMS is a way to make machine parts using automated technologies like CNC machines, robotic arms, etc. But, like any other system, the parts that make up AMS could stop working. If one of the computers stops working, the other one will take over right away. When a machine breaks down, it is sent to a shop where people work to fix it. But there are only so many repairmen, so if several machines break down at the same time, the shop can fall behind. If there were more delays, the company's operating costs would go up. Reneging is a behavior that costs the system more money because it makes the system less efficient. A person who is in charge of fixing broken equipment may decide to leave the line after waiting for a while. The word for this kind of rejection is "reneging." In the event that a machine breaks down and needs to be replaced by a standby machine, there is a window of time when switching errors can happen. Because of this, there is a chance of wrong switching, which could affect how the redundancy process works. Production manufacturing systems, encountered production manufacturing systems, and any other machining system must be able to find problems and fix them in order to lower the organization's total operating costs and make it more profitable. This question is about a common problem with machine maintenance in a setup that can switch between full-capacity operation and a shorter "short mode" shift depending on how many machines are available.

Operating machines in "short mode," which is when fewer machines are running than are needed for the normal operation of the system, have a higher failure rate than operating machines in "normal mode," which is when the right number of machines are running. This is because too many machines are sharing the load. In the field of queueing theory, this is often referred to as the "m,M policy." In this part, we'll put together a Markov model for three different uses. For the redundant machine repair problem, it is first necessary to come up with steady-state and transient-state performance indicators that take into account geometric reneging, standby switch failures, and a large number of repairmen. Some of the many system performance measurements that need to be set are the throughput of the system, the average number of running and standby machines, the average reneging rate and switching failure rate, machine availability and operative utilization, and many more. The mean time to failure (MTTF) and the number of times something breaks down are also measured. As the second step in our process, we make a cost model that looks at the best values for using repairmen and standbys at the same time in order to keep costs as low as possible. Third, we do sensitivity tests on the dependability characteristics to see how changing some of the system's parameters affects the overall performance. The goal of these analyses is to figure out how the changes will affect the reliability features.

II. REVIEW OF LITERATURE FOR MARKOV MODEL FOR MACHINE REPAIR SYSTEMS

Since the Markov model for machine interference in the textile industry was first introduced, many review papers have been written on this subject (Palm, 1943). Academics have paid a lot of attention to the question of machining systems with standby machines. Jain and Gupta made the perfect policy for a system that could be fixed. This plan was realistic because it included things like hazy fault coverage and breaks, which are common in the real world.

If a problem is found in a machined part, it may be replaced with a backup part that is just as easy to get. Having a backup plan in place makes sure that the system can keep running normally even if a part breaks down for no apparent reason. This gives the broken part time to be fixed or replaced. If an operating machine breaks down, it's hard to rule out switching failures that happen when the machine goes from "standby" mode to "operational" mode. Some academics looked at switch failure while making reliability models for problems with machine maintenance (cf. Kumar and Agarwal, 1980; Lewis, 1996; Wang et al., 2006; Wang et al., 2007; Wang and Chen, 2009). Jain and Rani (2013) looked into the performance of a multi-server, multi-component machining system by taking switching and failures caused by the same thing into account. Jain et al. (2014) used a matrix technique with successive over relaxation to figure out how well a redundant m, M machining system works when hot machines fail to switch. To do this, the differential difference equations that govern the system were made. Shekhar et al. looked at the mean time to failure (MTTF) and the availability of redundant machine repair when a switch fails and it takes a while to start up again (2014). Kuo and Ke looked at steady-state availability for repairable systems with standby switching failure (2016). Ke et al. (2016) were able to figure out how many backup computers to have on hand by using the Probabilistic Global Search Lausanne (PGSL) method. This was done so that the least expensive way to fix a broken standby switching mechanism in a computer could be found. The traditional reneging problem in machine repairs uses the amount of time spent waiting in line at the shop as a proxy for how likely it is that the machine's owner will give up and leave the machine (cf. Ke and Wang, 2002; Choudhury and Medhi, 2011). This chapter looks at a probabilistic form of reneging in a geometric setting. The goal is to study MRP with imperfect switching and standby support. Dimou and Economon used a single server queue with disasters following a Poisson distribution and geometric reneging to find the right formulas and a way to compute them (2013). Yang et al. (2015) used a standby system and an unstable server to find the best way to measure the dependability of a multi-component machining system. In this system, the number of machines that break down could go up by a factor of three. Shekhar et al. (2016) came up with the idea of geometric reneging queues to solve the problem of taking care of machines with N policies.

III. MARKOV MODEL

A. The Specifications of the Model

A Markov model with geometric type reneging has been made for the multi-component machining system, which includes the supply of spare parts and the multi-repair facility. In the mathematical description of the problem of maintaining the machine, the following points and assumptions are made: The machining system is made up of M different machines that work together as a single unit. You can always use one of the S heated standby machines in case of an emergency or a sudden break down. This is done to make sure that business will go on as usual. The system needs M operating computers in normal mode for optimal operation, although it can also operate in short mode with the right setting has m (? M) working machines;  The structure fails utterly if less than m (? M) machineries are in the functioning state also denote L ? M ? S ? m ?1.

Both the main machines and the backup machines have the same chance of breaking down, and their expected life spans follow the same exponential function ? and ? ?? ? ??, respectively. When all of the machines in the standby pool are being used and the system is in "short mode," the number of machines breaking down is cut down ?d because the machines that are left can't handle the work. So, the rate of failure of the devices as a function of state can be written as.

• If the switchover goes smoothly, a running machine that isn't working right will be replaced by a warm standby machine. A switched warm standby machine has the same chance of breaking down as an active machine.
• If the first try fails, more standby machines will try the switchover one at a time in a geometric pattern until either the switchover is successful or all the standby machines are used. The chance that a switch won't work is q .
• If either the main machine or the backup machine breaks down, it is quickly taken to the service station, where one of the R repairmen on call will make the needed changes. An exponential distribution shows that the average rate at which the technician fixes the broken equipment grows faster and faster ?.

B. Fixing Broken Equipment is Prioritized by the server according to the FIFO (First-in, First-out) rule.

• When a damaged computer is fixed, it works just like a new one and can instantly go into mode of operation or standby mode, depending if the operating system is in quick mode or regular mode.
• If a computer in the system isn't working right, the administrator may decide to take it out of the system one at a time, using a geometric distribution-based probability parameter ?. A parameterized exponential distribution is followed by the time required to renege r. Machine failure and routine maintenance are both random events that have nothing to do with each other. In particular, we need a mathematical overview of the current model right now so that we can t , the state of the structure Denoted  by the figure of botched machinery in the system at instance t i.e.                      

The status probability is distinct by.

 N ?t ? .

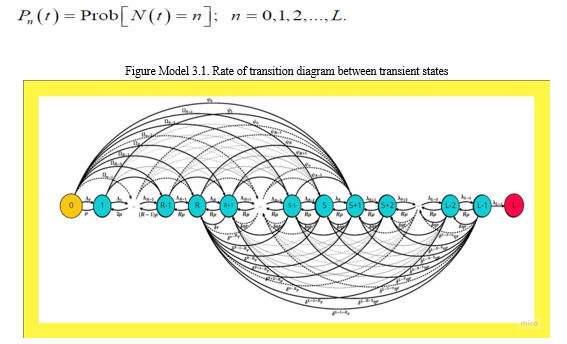
E. Results from Calculations and a Sensitivity Study

Up until now, performance has been described by the predicted value of irregular state vector based on state possible outcomes, reliability characteristics, and estimated total cost. In the tables and figures below, you can check that the calculated equations are correct and quickly get an idea of how to build the best machining system. For ease of calculation, the following defaults have been set for all parameters:

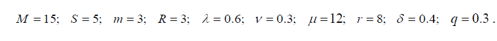
Figure 3.2 present the graph for the difference of the consistency of the scheme R Y??t?? with esteem to time t in the gap [0,100] unit time for a variety of system parameter. Figure 3.3(i)-3.3(vi) demonstrate the decrement of R Y??t?? as point in time grow. Other obvious results can be experiential from the Figure 3.2 in which reliability of the system decrease when the failure rate of working machines goes up, both the chance that a standby machine will break and the rate at which switching machines break go up by a lot. There is no doubt that a more advanced service center could make the system more reliable from Figure 3.2(iii). It is also experimental that the reliability of the structure is growing function of reneging rate r and reneging probability ??. So, the system's reliability goes up when broken machines choose to go to an outside repair shop for the same price instead of using it to fix their problems.

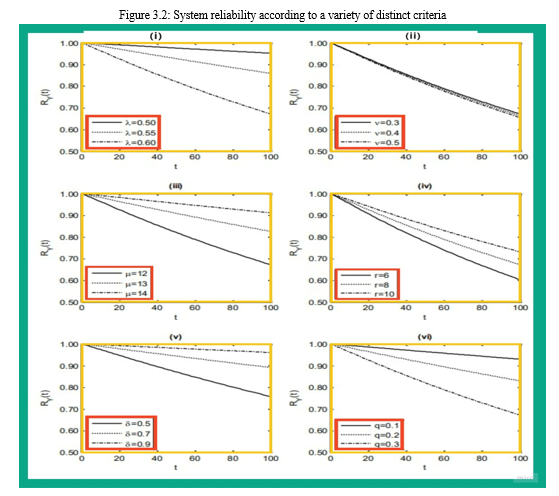
at this time, the relative sensitivity of the reliability ????process the proportion modify in the ? R Y??t?? has a strong judgment about the proportional shift in the structural descriptor ??. The growth or decrease in value may be explained by either the positive or negative sign of the asset. of R Y??t?? when there is growth in structural descriptor ??. Its magnitude reflects the degree of sensitivity that is associated with the pertinent structural parameters.. Figure 3.3(i) shows the same pattern that was seen in Figure 3.2; It seems that the structure's reliability will diminish in proportion to the value as it is increased of ??,??and q while it increase by rising the parameters ?, r and ??. Furthermore, it can be plainly shown that the dependability of the structure is responsive to the structure description included in the instruction r ???????????????q The outcomes of this study enable the system user to conclude that the preventative safeguarding instrument must be used routinely in order to keep up with the breakdown of operating machines and the switching failure of standby equipment.

References

[1] Beaudry, M. Danielle. \"Performance-related reliability measures for computing systems.\" IEEE Transactions on Computers 27.06 (1978): 540-547. [2] Bellman, Richard. Introduction to matrix analysis. Society for Industrial and Applied Mathematics, 1997. [3] Bobbio, Andrea, and Kishor S. Trivedi. \"An aggregation technique for the transient analysis of stiff Markov chains.\" IEEE Transactions on computers 35.09 (1986): 803-814. [4] de Souza e Silva, Edmundo, and H. Richard Gail. \"Calculating availability and performability measures of repairable computer systems using randomization.\" Journal of the ACM (JACM) 36.1 (1989): 171-193. [5] Donatiello, Lorenzo, and Balakrishna R. Iyer. \"Analysis of a composite performance reliability measure for fault-tolerant systems.\" Journal of the ACM (JACM) 34.1 (1987): 179-199. [6] Gear, C. William. \"Numerical initial value problems in ordinary differential equations.\" Prentice-Hall series in automatic computation (1971). [7] Fox, Bennett L., and Peter W. Glynn. \"Computing poisson probabilities.\" Communications of the ACM 31.4 (1988): 440-445. [8] Kulkarni, Vidyadhar G., Victor F. Nicola, and Kishor S. Trivedi. \"On modelling the performance and reliability of multimode computer systems.\" Journal of Systems and Software 6.1-2 (1986): 175-182. [9] Lambert, John Denholm, and John Denholm Lambert. Computational methods in ordinary differential equations. Vol. 5. John Wiley & Sons Incorporated, 1973. [10] Maire, Raymond A., Andrew L. Reibman, and Kishor S. Trivedi. \"Transient analysis of acyclic Markov chains.\" Performance Evaluation 7.3 (1987): 175-194. [11] Reibman, Andrew, and Kishor Trivedi. \"Numerical transient analysis of Markov models.\" Computers & Operations Research 15.1 (1988): 19-36. [12] Siewiorek, Daniel P. \"Multiprocessors: Reliability modeling and graceful degradation.\" Infotech State of the Art Conference on System Reliability. 1977. [13] Smith, Roger M. \"Markov reward models: Application domains and solution methods.\" (1989): 1809-1809. [14] Smotherman, Mark Kelly. Parametric error analysis and coverage approximations in reliability modeling. Diss. University of North Carolina at Chapel Hill, 1984. [15] Trivedi, Kishor Shridharbhai. Solutions manual: Probability and statistics with reliability, queuing and computer science applications. Prentice-Hall, 1982. [16] Van Loan, Charles. \"The sensitivity of the matrix exponential.\" SIAM Journal on Numerical Analysis 14.6 (1977): 971-981. [17] Wilkinson, J. H., and C. Reinsch. \"Singular value decomposition. Linear Algebra, vol 2. Handbook for automatic computation.\" (1971).

Copyright

Copyright © 2022 Sonam Bansal , Dr. Sharon Moses . This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.