Multiple Image Watermarking Approach Based on ANFIS for Copyright Protection and Image Authentication

Abstract

Watermarking software is one of the most important methods for protecting copyrights, certifying ownership, and combating software piracy. The advancement of communication technology has resulted in an enormous amount of digital data that needs to be protected. Watermarking is a technique for concealing private information in an original signal while improving its overall performance. Multipleiwatermarking, which involves inserting more than oneiwatermark into a singleimultimedia product, is another hot topic in the world of digital picture watermarking. Using simply a digital watermarking approach, a trademark or copyrightmessage is discreetly inserted in the medical image. Many academics have collaborated to create ANFIS, which includes a watermark in the principal (cover) image. Watermarking embedding locations can be chosen based on regions of interest (ROIs). We first deconstruct the cover image into four sub-bands with 3-L LWT, then modify the singular values inside each band with SVD. Following various attacks on the watermarked image, such as blurring, addinginoise, pixelation, rotation, rescaling,icontrast adjustment, gammaicorrection, histogram equalisation, cropping,isharpening, lossy compression, and so on, the original insertediwatermark image is extracted from allibands and compared using MSE and PSNR values. The trials reveal that changing all frequencies makes our watermarked image more resistant to a wide range of image processing attacks (including standard geometric attacks), i.e. we can effectively recover the watermark from some of the four sub-bands using ANFIS.

Introduction

I. INTRODUCTION

Due to the rapid growth of internet activity, a great deal of digital information is widely distributed. Digital watermarking was developed to hide digital data while protecting the copyright of multimedia signals including audio, video, and photos. Because the discrete-time wavelet transform (DWT) provides a useful platform, many DWT-based algorithms for digital watermarking have been presented in recent years. Watermarking in the spatial domain [1–11] is often more fragile than watermarking in the frequency domain [12–29] with the same embedding capacity, due to the fact that spatial-domain approaches are generally more vulnerable to image-processing operational processes and other attacks [23–25]. The spatial-domain singular value decomposition (SVD) for picture watermarking was first introduced by Liu et al. [8]. By modifying the singular values of the host image in the spatial domain using a spread-spectrum approach, the authors were able to insert a watermark in this work. Some authors attached watermarks to U and V components to boost embedding capacity [9, 10], whereas Ghazy et al. [11] suggested a blockby-block SVD-based image-watermarking approach. The spatial domain robustness of SVD-based picture watermarking, on the other hand, is restricted. In recent years, many image-watermarking techniques have merged DWT with SVD to improve transparency and robustness [17, 18, 24, 25]. Bao et al. [17] proposed a novel, yet basic, picture-adaptive watermarking system for image authentication by employing a simple quantization index-modulation technique on each single unique value of the blocks in the wavelet domain. Their watermarking method is blind and resistant to JPEG compression, but it is especially prone to malicious manipulations such as filtering and random noise. Ganic et al. [18] applied SVD to all details, approximating a portion of the DWT, and the watermark picture to increase embedding capability. Gaurav and Balasubramanian [24] implanted a watermark into the reference image by replacing the singular values of the reference image with the singular values of the watermark. The robustness has been improved slightly. On the other hand, the computation has been substantially improved. Lai and Tsai [25] simplified the algorithm in [24] by directly embedding the watermark into the singular values in the wavelet domain. We divide the DWT middle frequency components LH3 and HL3 into several square blocks to obtain huge embedding capacity. Rather than employing a spread-spectrum technique on single singular values, we use several singular value quantizations to include a watermark bit [24, 25].

While keeping a high embedding capacity, it achieves remarkable resistance to median filtering. On the other hand, an optimal quality formula is proposed by reducing the difference between original and watermarked singular values. As a matriced performance statistic, the peak signal-to-noise ratio (PSNR) is first established. Using an optimised quality functional, the performance index is then linked to the quantization technique. Finally, the Lagrange Principle is employed to generate a high-quality formula that is then used to make watermarks. Experiments show that the watermarked image can maintain a high PSNR and achieve a better bit error rate even as the number of coefficients for embedding a watermark bit rises (BER). The resistance to median filtering, in particular, has improved dramatically. The following is a breakdown of the structure of the paper. In Section II, we go through some mathematical fundamentals. Section III goes over the suggested watermark embedding and extraction methods. In Section IV, PSNR is rebuilt as a performance index. The optimized-quality issue, which is based on an optimized-quality equation that relates the performance index to the quantization restriction, is frequently solved using the Lagrange Principle. The solution is used to embed the watermark, and the effect is fantastic: the watermark can be retrieved without the original image being removed. In Section V, we present some experiments and a performance table to evaluate the proposed scheme's performance. Finally, conclusions are drawn in Section VI.

II. PRELIMINARIES

Some associated stages for the suggested image watermarking technique are reviewed in this section.

A. Discrete-Time Wavelet Transform (Dwt)

The wavelet transform (WT) is widely used in signal analysis, both stationary and nonstationary. The removal of electrical noise from signals, the detection of abrupt discontinuities, and the compression of vast volumes of data are all examples of these uses. As seen by publications published in the literature [31–33], the use of WT in corrosion experiments is not uncommon.

Similar to the Fourier transform (FT), which represents a signal with sine and cosine functions of limitless duration, the WT can split a signal into a number of constituent signals known as wavelets, each with a well defined, dominating frequency. Wavelets are short-duration transient functions in WT, that is, functions with a restricted duration centred around a certain time. The FT's drawback is that information about what happens in time is lost while moving from the time domain to the frequency domain. It is straightforward to discern the frequency content of the signal being studied by looking at the frequency spectrum acquired using the FT, but it is not able to determine when the components of the signal in the frequency spectrum appear or depart. Unlike the FT, the WT allows for analysis in both the time and frequency domains, providing data on the evolution of a signal's frequency content over time [34]. The WT has been discretized, just like the FT, and is now known as a discrete wavelet transform (DWT), which offers a significant benefit over classic FT approaches. The WT decomposes a signal into numerous scales representing distinct frequency bands, and the position of the WT at each scale can be established at the critical time characteristic with which the electrical noise may be identified and removed successfully. Information can be retrieved from high-frequency components using short-time wavelets. Electrical noise is more likely to exhibit high-frequency variations, therefore this knowledge is crucial for removing it [35]. Low-frequency information can be extracted using long-term wavelets. We can create a threshold and zero the frequencies below the unwanted threshold of the electric noise using the high and low frequency information [36].

Donoho and Johnstone [36] proposed the use of a threshold for the removal of Gaussian white electrical noise in signals, which led to the pioneering work of removing electrical noise from signals using the WT. Similar works, but using the undecimated discrete wavelet transform (UWT), are presented subsequently, allowing for the elimination of electrical noise using a nonlinear technique proposed by Coifman and Donoho [37].

The DWT is considered a suitable tool for the elimination of electric noise as a novel alternative to procedures of attenuation of electrical noise with the use of low-pass filters of systems Lock-In Amplifier or fast Fourier transform (FFT) that alone can be used in circumstances where the electrical noise has a very small overlap of bands or is completely different and separated from the signal and noise to be able to use the method of filtering,

The Discrete Fourier Transform (DFT) decomposes a signal into sinusoidal basis functions of various frequencies in Fourier analysis. This transformation does not lose any information; in other words, the original signal may be fully recovered from its DFT (FFT) representation. The Discrete Wavelet Transform (DWT) decomposes a signal into a set of mutually orthogonal wavelet basis functions in wavelet analysis. These functions differ from sinusoidal basis functions in that they are spatially localised, meaning that they are nonzero only across a portion of the whole signal duration. Wavelet functions are also dilated, translated, and scaled variants of the mother wavelet, which is a common function. The DWT is invertible, just like Fourier analysis, therefore the original signal can be reconstructed completely from its DWT form. Unlike the DFT, the DWT refers to a collection of transforms, each with its own set of wavelet basis functions. The Haar wavelets and the Daubechies wavelets are two of the most popular.

It is important to note the following important properties:

1. Wavelet functions are spatially localized;
2. Wavelet functions are dilated, translated and scaled versions of a common mother wavelet; and
3. Each set of wavelet functions forms an orthogonal set of basis functions.

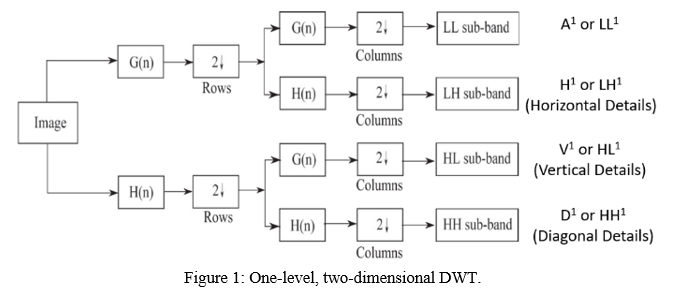
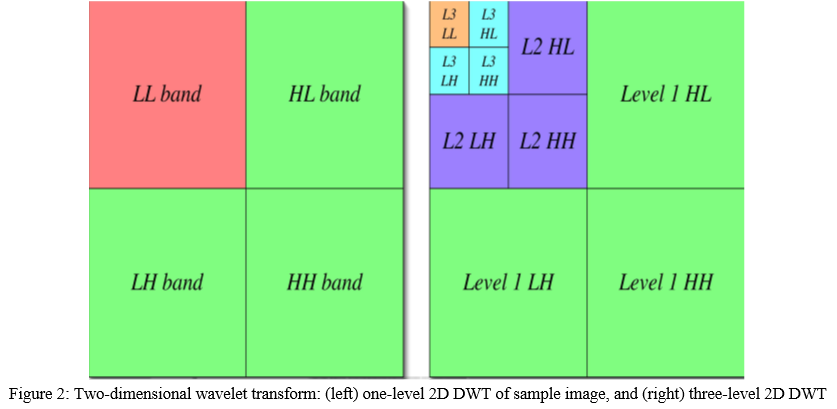
The fundamental, one-level, two-dimensional DWT technique is shown in Figure 1. First, we run a one-level, one-dimensional DWT across the image's rows. Second, along the columns of the altered image from the first step, we apply a one-level, one-dimensional DWT. The consequence of these two sets of processes, as shown in Figure 2 (left), is a modified image with four unique bands: (1) LL, (2) LH, (3) HL, and (4) HH. The letters L and H stand for low-pass and high-pass filtering, respectively. The LL band generally corresponds to a two-fold downsampled rendition of the original image. In the original image, the LH band tends to maintain localised horizontal characteristics, while the HL band tends to preserve localised vertical features. Finally, the HH band isolates high-frequency point features in the image that are confined.

We don't necessary want to stop there, as in the one-dimensional example, because the one-level, two-dimensional DWT retrieves only the highest frequencies in the image. Lower frequency features in the image can be extracted using additional layers of decomposition; these new levels are applied solely to the LL band of the converted image at the previous level. Figure 2 (right) shows a three-level, two-dimensional DWT applied to a sample image.

B. Singular Value Decomposition (Svd)

The singular value decomposition (SVD) of a mn real - valued function matrix A with m n continues to perform analagous row and column functions on A in such a manner that the ensuing matrix is tangential, and diagonal results (singular values) are organised in reducing value and relate with the square root of AT*T Eigen values [49]. The columns of the millimeter, U matrix, as well as the sections of the nn, V structure, have mutually perpendicular unit vectors. The matrix U and V are diagonal, i.e.

S is a pseudo-diagonal matrix with absolute scores for main diagonal. We can re-create the diagonal A by adopting following method:

The SVD approach has a few key qualities that make it ideal for digital watermarking:

III.ADAPTIVE NEURO FUZZY INFERENCE SYSTEMS (ANFIS)

An ANFIS blends fuzzy logic with neural network techniques to create a fuzzy inference system. ANFIS is a fuzzy logic inference system based on Takagi-Sugeno fuzzy logic inference systems. To get the best value for the fuzzy inference system's design variables, an artificial neural network is used. By training the artificial neural network with data sets, the fuzzy inference system has acquired an adaptable property. A hybrid strategy is used to train the neural network, which combines the well-known back-propagation active learning method with the regression method [38].

The following features of ANFIS controllers make them ideal for nonlinear and time-varying applications:

1. Because of its adaptable capability, it is directly applicable to adaptive control.
2. Capacity to learn
3. Effective Knowledge representation that is structured
4. Improved compatibility with various control design techniques
5. Parallel operation flexibility.

ANFIS permits data sets to be used to determine the rule base and membership functions for this purpose.

Because of the ANFIS design, the rules can be built but with a decompositional technique. ANFIS is a multi-layer feed-forward network that can be divided into two types: adaptive and fixed networks. On the received signal, each node (neuron) performs a specific function. The rules are retrieved at the neural network's individual node level, then aggregated to reflect the system's overall dynamics (Jang 1993). Fuzzy if-then rules with appropriate membership functions provide the first stated input-output pairings, and these membership functions acquire their final forms over training thanks to regression and optimization approaches.

The gradient vector is a measurement of how effectively the system imitates the specified training data set for a variety of parameters. Optimization methods are used to change the parameters after getting the gradient vector in order to decrease a defined error criteria. The system conforms whenever the training and checking mistakes are still within an acceptable range.

The first-order Sugeno fuzzy model will be used to illustrate the blind control system because it is a first-order process. We shall employ the first order Sugeno fuzzy model for dynamic application again because of its effectiveness and accountability (Zilouchian and Howard 2001). Sugeno models with more levels of complexity add to the system's complexity without adding much value. As a result, the blind control system [66] is configured as a first-order system.

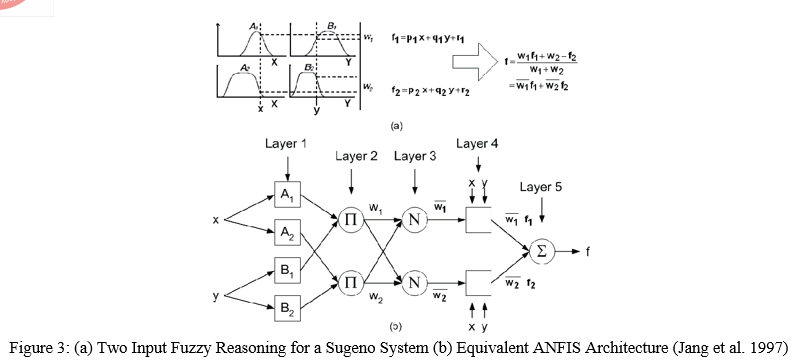
Because there is no computationally difficult defuzzification technique, each rule has crisp output, as illustrated in Figure 4.4 (a) on the linked page, and the total output is calculated using a weighted average to reduce calculation time. The crisp output was necessary whenever the fuzzy system was employed as a controller. Because of these features, the Sugeno system is the most popular choice for sample-based fuzzy modelling, which we used in our study.

A two-input first-order sugeno fuzzy model with two rules is shown in Figure 3. (a). The rule basis of a two-rule fuzzy set is supplied by

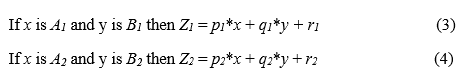
IV. OPTIMIZATION SOLVER

Some optimization strategies are given in [29–31] to identify the extreme of the matrix function. The matrix function's operations are first demonstrated as follows:

1. Extract a four-bit block from the secret image in question (s)
2. Create a four-bit covert image block set for each block.
3. Retrieve the next progressively possible 2x2inon overlapping sub block matrix of either the cover image and apply forward transformation with the very first three pixel bytes as shown here, leaving the fourth pixel byte alone, in row major order. Consider that the digits to the right of the relevant sub matrix number M are [D5D4D3D2D1D0], with a 512x512 colour cover image having up to 6 digits.
4. Extract the concealed bits one by one, starting with four-bit blocks.

Calculate the next immediate bigger multiple value of (N+4) w.r.t the matrix integer M as R as well as the LSB location P for bit placement utilising the two top right MSB bits of the transformed pixel byte to conceal a bit throughout the first transformed matrix element.

Determining the LSB position L value for bit insertion as a means of hiding a bit in the second conversion elementL=[((D5+D4+D3+D2+D1+D0)%4+(D1D0)%4)x(D5+D4+D3+D2+D1+D0) +Ke+Kf]%4.

There's a little something concealed inside the third modified matrix element. A concealed bit is hidden using the fourth matrix element. Execute inverse transformation on the initial three bit embedded matrix component data.

If necessary, change the values of the intermediate matrix components to keep their exact values inside the spatial domain ranges (0-255).

(5) Repeat the first and second stages until all of the hidden image's secret bits have been devoured.

(6) Stop.

The steps of extraction process are as follows,

1. Readinext consecutive 2x2inon overlappingisub matrix.

2. For eachisuch sub blockimatrix do the followingitasks

               2.1 Apply forwarditransform on the firstithree matrix elements asiin Fig1 and separate theiriinteger part.

               2.2. Extractibit from the firsticoded matrixielement.

               2.3 Extract bit from the second coded matrix element.

               2.4 Extract bitifrom the third codedimatrix element.

               2.5 Extractibit from the fourthicoded matrixielement.

               2.3 Arrange theifour extracted secret bitsiin proper order orisequences to form the secretiwatermark image.

3. Repeatistep1 and step2 for completioniof the total secretibit extraction processias per the size of theiwatermark images.

4. Stop.

V. PROPOSED WATERMARKING SCHEMES

The proposed watermarking scheme is introduced in this section. The watermark is extracted without the original image.

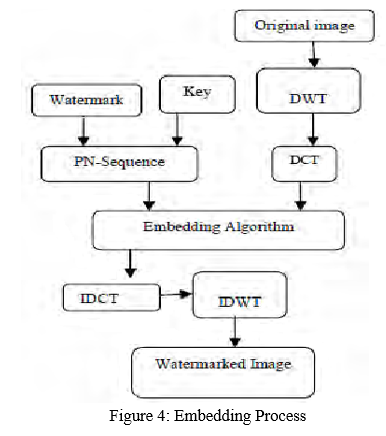
A. Embedding Algorithm

1. Input: Cover Image and Watermark Image
2. Output: Watermarked Image

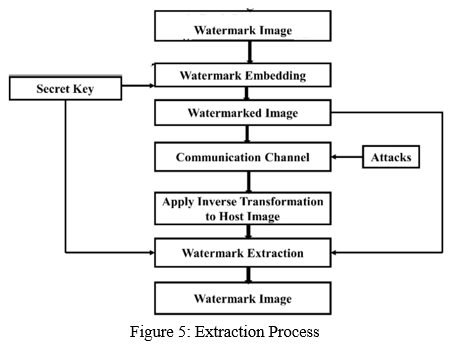
B. Extraction Algorithm

1. Input: Watermarked Image
2. Output: Attacked Image

VI. RESULTS

Original image or input images have a RGB combination. Image processing begins with an image acquisition process. The two elements are required to acquire digital images.

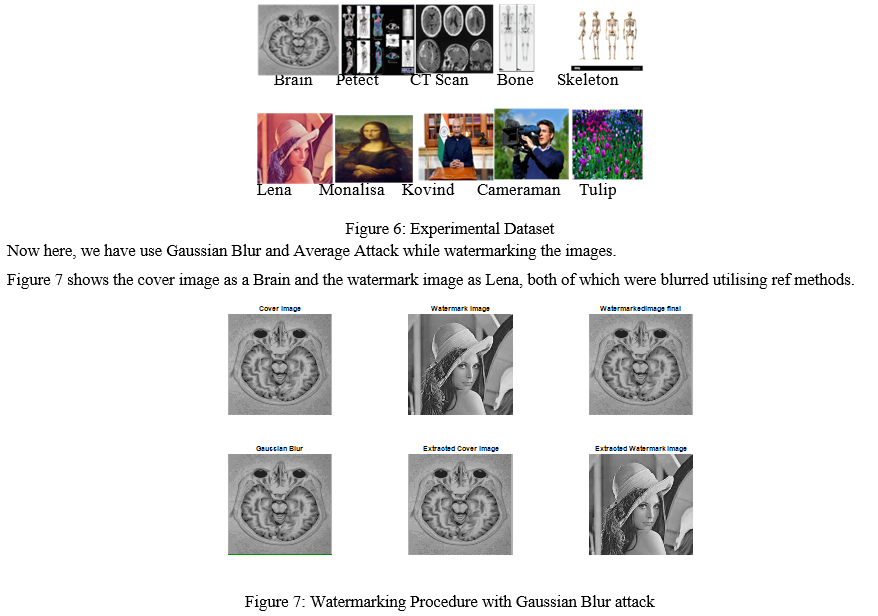
The following figure 6 has been taken to test the system.

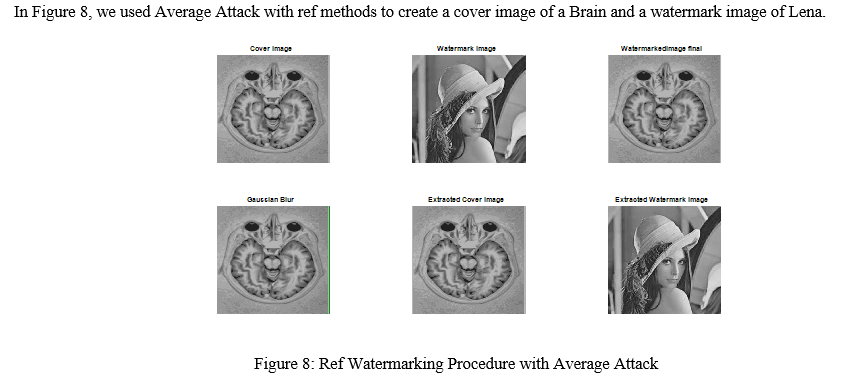
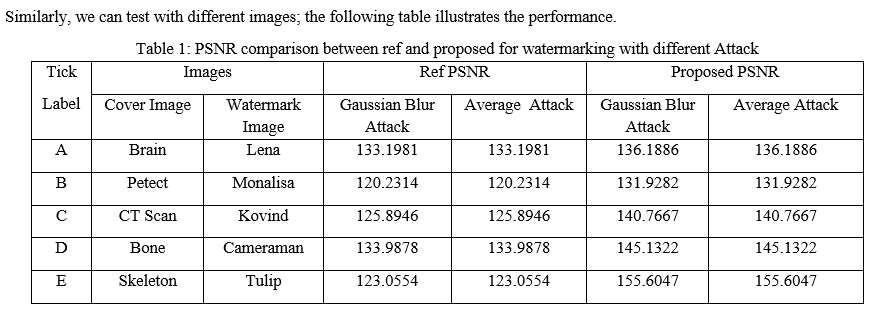
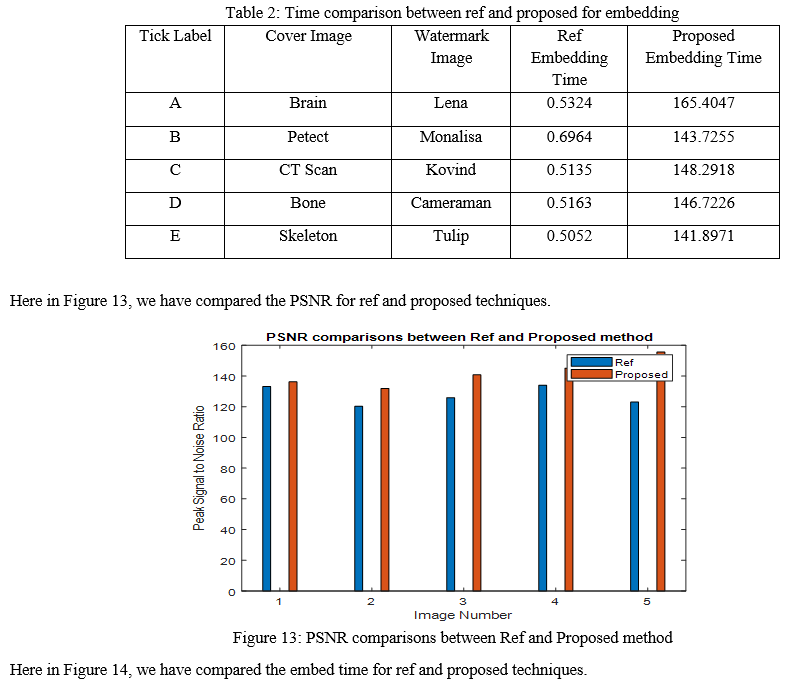
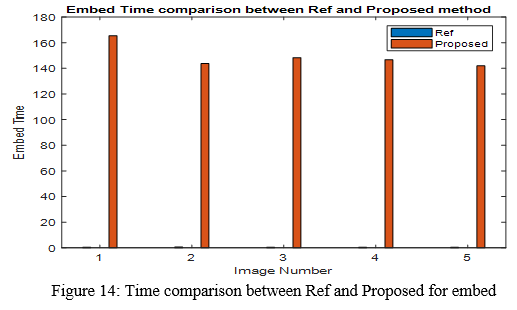
The purpose of calculating the performance of the image and after that comparison between ref and proposed methods will show which method is better for image watermarking. Such method is mainly due to highly accurate detection with various attacks. The (Peak signal to noise ratio) PSNR, (Signal to noise ratio) SNR is high; (mean squared error) MSE is low. This proposed method is a fast method for image watermarking.

Conclusion

This study used optimization-based quantization on multiple singular values in the wavelet domain to increase the robustness of classical SVD-based Digital image watermarking. Experiments indicate that even when the number of coefficients for embedding a watermark bit increases, the watermarked image can maintain a high PSNR and obtain a lower MSE. The robustness against JPEG compression, Gaussian noise, and median filtering has all improved greatly. The topic of strengthening robustness against rotation will be the focus of future work.

References

[1] U. Mustafa, U. Guzin and V. V. Nabiyev, “Medical image secu-rity and EPR hiding using Shamir\'s secret sharing scheme,” Journal of Systems and Software, vol. 84, no. 3, pp.341-353, 2011. [2] M Alghoniemy, AH Tewfik, Geometric distortion correction in image watermarking, in Proceedings SPIE Security and Watermarking of Multimedia Contents II 3971, 2000, pp. 82–89 [3] G. Coatrieux, C. L. Guillou, J. M. Cauvin, and C. Roux, “Re-versible watermarking for knowledge digest embedding and re-liability control in medical images”, IEEE Transactions on In-formation Technology in Biomedicine, vol. 13, no. 2, pp.158-169, 2009 [4] B Chen, GW Wornell, Quantization index modulation: a class of provably good methods for digital watermarking and information embedding. IEEE Trans. Inf. Theory 47, 1423–1443 (2001) [5] S. Makhmasi, F. Taher, H. Al-Ahmad and T. McGloughlin, “A novel multiple watermarking algorithm for patient identification and integrity control,” UKSim-AMSS 17th International Con-ference on Modeling and Simulation, UK, 2015 [6] MU Celik, G Sharma, AM Tekalp, E Saber, Lossless generalized-LSB data embedding. IEEE Trans. Image Process. 14(2), 253–266 (2005) [7] LC Lin, YB Lin, CM Wang, Hiding data in spatial domain images with distortion tolerance. Elsevier: Computer Standards and Interfaces 31, 458–464 (2009) [8] Y. A. Y. Al-Najjar and D. C. Soong, “Comparison of image quality assessment: PSNR, HVS, SSIM, UIQI,” International Journal of Scientific and Engineering Research, vol. 3, no. 8, pp. 1-5, 2012 [9] C-C Chang, P Tsai, C-C Lin, SVD-based digital image watermarking scheme. Pattern Recogn. Lett. 26(10), 1577–1586 (2005) [10] KL Chung, WN Yang, YH Huang, ST Wu, YC Hsu, On SVD-based watermarking algorithm. Application. Math. Comput. 188, 54–57 (2007) [11] RA Ghazy, NA El-fishawy, MM Hadhoud, MI Dessouky, FEA El-Samie, An efficient block-by-block SVD-based image watermarking scheme, in 2007 Radio Science Conference, Cairo, 2007, pp. 1–9 [12] SF Lin, SC Shie, JY Guo, Improving the robustness of DCT-based image watermarking again JPEG compression. Elsevier: Computer Standards and Interfaces 32, 57–60 (2010) [13] S. S. M. Ziabari, “Enhancement of genetic image watermarking robust against cropping attack,” International Journal in Founda-tions of Computer Science and Technology, vol. 4, no. 2, pp. 21-26, 2014 [14] H Qaheri, A Mustafi, S Banerjee, Digital watermarking using ant colony optimization in fractional fourier domain. J. Inform. Hiding. Multimedia. Signal. Process. 1(3), 179–189 (2010) [15] CH Manuel, GU Francisco, NM Mariko, HM Pérez-Meana, Robust hybrid color image watermarking method based on DFT domain and 2D histogram modification. Springer: Signal Image and Video Processing 8(1), 49–63 (2014) [16] M. A. Suhail and M. S. Obaidat, “Digital Watermarking-Based DCT and JPEG Model,” IEEE Transactions on Instrumentation and Measurement,vol. 52, no.5, pp. 1640-1647, 2003 [17] P Bao, X Ma, Image adaptive watermarking using wavelet domain singular value decomposition. IEEE Transactions on Circuits and Systems for Video Technology 15(1), 96–102 (2005) [18] E Ganic, AM Eskicioglu, Robust embedding of visual watermarks using DWT-SVD. J. Electronic. Imaging. 14(4), 1–13 (2005) [19] A. Nikolaidis and I. Pitas, “Asymptotically optimal detection for additive watermarking in the DCT and DWT domains,” IEEE Trans. on Image Processing, vol. 12, no. 5, pp. 563–571, 2003. [20] CT Li, Reversible watermarking scheme with image-independent embedding capacity. IEEE Proceedings on Vision, Image, and Signal Processing 152(6), 779–786 (2006) [21] CV Serdean, MK Ibrahim, A Moemeni, MM Al-Akaidi, Wavelet and multiwavelet watermarking. IET Image Process. 1(2), 223–230 (2007) [22] C-Y. Lin, M. Wu, J.A. Bloom, M.L. Miller, I.J Cox, and Y.M. Lui, “Rotation, Scale, and Translation Resilient Watermarking for Images,” IEEE Transactions on Image Processing, vol. 10, no. 5, pp. 767-782, May 2001. [23] N Li, X Zheng, Y Zhao, H Wu, S Li, Robust algorithm of digital image watermarking based on discrete wavelet transform. International Symposium on Electronic Commerce and Security, 2008 [24] B Gaurav, R Balasubramanian, A new robust reference watermarking scheme based on DWT-SVD. Elsevier: Computer Standards and Interfaces, 2009, pp. 1–12 [25] CC Lai, CC Tsai, Digital image watermarking using discrete wavelet transform and singular value decomposition. IEEE Trans. Instrum. Meas. 59(11), 3060–3063 (2010) [26] S. Voloshynovskiy, F. Deguillaume, and T. Pun, “Multibit digi-tal watermarking robust against local nonlinear geometrical dis-tortions,” In IEEE International Conference on Image Pro-cessing, ICIP, pp. 999-1002, Thessaloniki, Greece, 2001. [27] K Loukhaoukha, JY Chouinard, MH Taieb, Optimal image watermarking algorithm based on LWT-SVD via multi-objective and colony optimization. J. Inform. Multimedia. Signal. Process. 2(4), 303–319 (2011) [28] A Mishra, C Agarwal, A Sharma, P Bedi, Optimized gray-scale image watermarking using DWT- SVD and firefly algorithm. Elsevier: Expert Systems with Applications 41, 7858–7867 (2014) [29] S-T Chen, H-N Huang, W-M Kung, C-Y Hsu, Optimization-based image watermarking with integrated quantization embedding in the wavelet domain. Springer: Multimedia Tools and Applications, 2015. doi:10.1007/s11042-015-2522-8 [30] S-T Chen, G-D Wu, H-N Huang, Wavelet-domain audio watermarking scheme using optimisation-based quantisation. IET Proceedings on Signal Processing 4(6), 720–727 (2010) [31] S-T Chen, H-N Huang, C-C Chen, K-K Tseng, S-Y Tu, Adaptive audio watermarking via the optimization point of view on wavelet-based entropy. Elsevier: Digital Signal Processing, 2013, pp. 971–980. [32] L. A. Montejo and L. E. Suárez, “Aplicaciones de la Transformada Ondícula (“Wavelet”) en Ingeniería Estructural,” in Mecanica Computacional, vol. XXVI, pp. 2742–2753, Córdoba, Argentina, October 2007. [33] M. Bitenc, D. S. Kieffer, and K. Khoshelham, “Evaluation of wavelet denoising methods for small-scale joint rougness estimation using terrestrial laser scanning,” in Proceedings of the ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, vol. II-3/W5, ISPRS Geospatial Week 2015, La Grade Motte, France, 28 Sep–03 Oct 2015, 28 Sep-03 Oct 2015. [34] S. G. Chang, B. Yu, and M. Vetterli, “Adaptive wavelet thresholding for image denoising and compression,” IEEE Transactions on Image Processing, vol. 9, no. 9, pp. 1532–1546, 2000. [35] D. L. Donoho and J. M. Johnstone, “Ideal spatial adaptation by wavelet shrinkage,” Biometrika, vol. 81, no. 3, pp. 425–455, 1994. [36] D. L. Donoho, “De-noising by soft-thresholding,” IEEE Transactions on Information Theory, vol. 41, no. 3, 1995. [37] R. R. Coifman and D. L. Donoho, Translation-Invariant De-Noising, Spriger, New York, USA, 1995. [38] G. C. Goodwin and K. S. Sin. Adaptive filtering prediction and control. Prentice-Hall, ENglewood Cliffs, N.J., 1984

Copyright

Copyright © 2022 Anmol Awasthi, Madhu Lata Nirmal. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.