Ijraset Journal For Research in Applied Science and Engineering Technology

Abstract

Neural Cryptography is a new thread that integrates cryptography and neural networks for cryptanalysis and encryption applications. We show that Neural Networks can execute symmetric encryption in an adversarial context in this paper, and we build on the existing literature on the subject. Cryptography\'s purpose is to make it difficult to decipher a cypher and recreate the plain text without the associated key. Your messages are encrypted with excellent cryptography in such a way that brute force attacks against the algorithm or key are nearly impossible. Good cryptography is secure because it employs extremely long keys and encryption techniques that are resistant to various types of attack. The neural net application is the next step in the evolution of good cryptography. This paper discusses the use of neural networks in cryptography, including how to create neural networks that can be utilized in cryptography.

Introduction

I. INTRODUCTION TO CRYPTOGRAPHY

The creation of new security methods that safeguard anyone from trespasser reading is the focus of cryptography. Data privacy systems are referred to as "cypher systems." The cypher key is a set of rules that are used to encrypt all data. The process of transforming open text, such as a message, into encrypted text using rules is known as encryption. Cryptanalysis of the news is the inverse technique, in which the recipient of the encryption converts it back to the original text. The cypher key must comprise a number of crucial qualities. The best illustration is the singularity of encryption and cryptanalysis. Letters, digits, and punctuation marks in the international alphabet are all the same. All the while with mystery of data the propensity for perusing the code news without realizing the code key was advanced. Code keys were observed intently. The primary objective of cryptology is to figure the code news and to recreate the utilized keys with the assistance of good examination of code news. It utilizes numerical insights, variable based math, numerical phonetics, and so on, just as realized slip-ups made by figures as well. The legitimateness of the open text and the applied code key are reflected in each code framework. Further developing the code key assists with diminishing this legitimacy. The wellbeing of the code framework lies in its insusceptibility against interpretation.

The objective of cryptanalysis is to make it conceivable to take a code message and imitate the first plain message without the comparing key. Two significant strategies utilized in encryption are symmetric and hilter kilter encryption. In symmetric encryption, two gatherings share a solitary encryption-unscrambling key (Khaled, Noaman, Jalab 2005). The sender scrambles the first message (P), which is alluded to as plain message, utilizing a key (K) to create an obviously irregular hogwash, alluded to as code message (C), i.e.:[4]

                              C = Encrypt (K,P)

When the code text is created, it can be sent. Upon receipt, the code text can be changed back to the first plain text by utilizing a decoding calculation and the very key that was utilized for encryption, which can be communicated as follows:

                              P = Decrypt (K,C)

In asymmetric  encryption, two keys are utilized, one key for encryption and one more key for unscrambling. The length of a cryptographic key is quite often estimated in bits. The more pieces that a specific cryptographic calculation permits in the key, the more keys are conceivable and the safer the calculation becomes.[4]

A. Introduction to Symmetric Encryption

Symmetric encryption is a type of encryption in which the sender and receiver use the same key to encrypt and decrypt plaintext and ciphertext, respectively.[4] Block or stream cyphers have traditionally been employed in symmetric encryption algorithms. It has been shown, however, that with end-to-end adversarial training, a system of neural networks may learn how to conduct types of 'encryption' and 'decryption' without the usage of a specific cryptographic algorithm.[4]

???????B.  Introduction to Artificial Neural Networks

A neural organization is an organization or circuit of neurons, or in this day and age, a counterfeit neural organization consisting of fake neurons or hubs.[1] Along these lines, a neural organization can be either natural (composed of natural neurons) or counterfeit (composed of fake neurons) and used to tackle computerized reasoning (AI) challenges. Counterfeit neural organizations model the associations of natural neurons as loads between hubs. An excitatory connection has a positive weight, while inhibitory associations have a negative weight. A weight is applied to all contributions before they are added. A direct mix is the name for this action.Finally, the yield's sufficiency is constrained by actuation work.[1][2] For example, an adequate yield range is ordinarily somewhere in the range of 0 and 1, in spite of the fact that it may likewise be somewhere in the range of 1 and 1.

II. LITERATURE SURVEY

1. A Neural Network based Approach for Cryptographic Function Detection:-

They suggested an unique neuralnet-based technique for identifying cryptographic features in malware in this research, and we constructed a prototype system. Their design is made up of two key parts: Instruction-2-vec, which extracts the semantic information from assembly instructions and converts it into 100-dimensional vectors, and an enhanced neural network. K-Max-CNN- Calculate function embeddings and complete the process of categorizing cryptographic functions with care.

2. Deep Neural Networks based key concealment schemes

To keep the Internet-of-things (IoT) environment secure, employing a cryptographic function to various IoT devices has become vital. An important factor to consider is how to store a cryptographic key (or passwords) securely. A popular method is to store the key in the storage protected by some hardware-based security functions. This paper presents a novel concept to conceal cryptographic keys into deep neural networks (DNNs), named DNNs-based key concealment scheme. In this scheme, a key can be concealed into a proper deep neural network model which is trained with secret input data. We demonstrate the practical applicability of our concept by presenting an instance and a use-case scenario of the DNNs-based key concealment scheme and show its correctness. To prove its robustness, two fundamental security evaluation methods are proposed for investigating the security of the instantiation. To the best of our knowledge, this is the first attempt of its kind.

3. Neural Cryptography based on Complex Valued Neural Networks

A public key exchange technique based on the notion of neural network synchronization is known as neural cryptography. The two neural networks adjust their own weight by sharing output from each other using a neural network's learning method. The weights of the two neural networks are the same after the synchronization is complete. The secret key may be created using the neural network's weights. All existing research, on the other hand, is based on the real-valued neural network paradigm. Rarely are papers on neural cryptography based on a complex-valued neural network model published. A neural cryptography based on the complex-valued tree parity machine network is presented in this technical note.

4. Neural Cryptography Based on Topology Evolving Neural Networks

Mathematical theory is used to build modern encryption methods. Recent research demonstrates a new approach in cryptography based on neural networks. A cryptographic scheme is developed automatically rather than knowing a specific technique. While one type of neural network is employed to implement the method, it is uncertain if the notion of neural cryptography can be accomplished using other neural network design. This attribute is used in this study to develop a neural cryptography scheme based on the Spectrum-diverse unified neuroevolution architecture, a novel topology changing neural network architecture.

5. Neural Cryptography: From symmetric encryption to Adversarial Steganography

Neural Cryptography is an emergent field that aims to combine cryptography with Neural Networks for applications in cryptanalysis and encryption. They (1) demonstrate that Neural Networks may perform symmetric encryption in an adversarial scenario and improve on the existing research on the subject in this study.

They also (2) demonstrate that by putting Neural Networks through known cryptographic games based on Ciphertext Indistinguishability, they may discover known cryptographically unsafe communication. Finally, they (3) discuss more work in Neural Steganography, including building neural end-to-end steganographic (imagein-image, text-in-image, video-in-video) algorithms in the face of adversarial networks seeking to censor.

6. Use of Neural Networks in Cryptography: A Review

Secret information is made illegible for unauthorized users using cryptography. Many cryptographic methods exist, but they are more complicated procedures that demand more processing capacity. This study examines how neural networks aid cryptography and how neural networks and cryptography may be used together to improve security.

7. Neural Network based Cryptography

The use of neural networks for cryptography is demonstrated in this study. There are two steps to the system. In the first stage, neural network-based pseudo-random numbers (NPRNGs) are generated, and the outputs are checked for randomness using randomness tests developed by the National Institute of Standards and Technology (NIST).

8. Cryptography based on Neural Networks

The neural net application is the next step in the evolution of excellent cryptography. This paper discusses the use of neural networks in cryptography, including how to create neural networks that can be utilized in cryptography. An experimental demonstration is also included in this publication.

9. Cryptography using Artificial Neural Networks

Different neural network topologies for an Adder are compared, and their benefits and drawbacks are highlighted. A finite state sequential machine was successfully developed using a Jordan (Recurrent network) trained using the back-propagation technique. The resulting sequential machine was utilized for encryption, with the initial key serving as the decryption key. A chaotic neural network with weights determined by a chaotic sequence was also used to accomplish cryptography.

10. Neural Cryptography

The first iteration of ANNs in cryptography was addressed in this study, as well as its advantages over other approaches (symmetric encryption)

III. PROPOSED MODEL

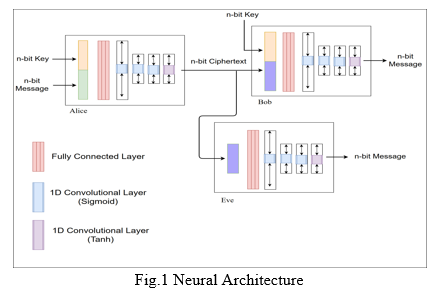
The proposed project aims to create three neural networks, Alice, Bob and Eve. Alice and Bob participate in a conversation protected by symmetric encryption. Simultaneously, Eve eavesdrops the conversation. As a result both the receiver and Eve have access to the cipher-text. However, the receiver does have the associated n-bit key. On the other hand, Eve doesn’t have the associated key. While the receiver deciphers the cipher text, Eve does try to decrypt without the associated key.[3][5]

???????A. Dataset

The dataset consists of two equally sized randomly generated strings: one as the plaintext and the second that functions as its associated keys. A uniform random distribution is achieved for this purpose. The generated keys and plaintext have the same length of N bits. The lengths may be 16, 32 or 64 bits. The length may be picked randomly out of the three values.

???????B. Artificial Neural Networks

Artificial neural networks consist of a pool of simple processing units that communicate with each other by sending signals to each other over a  number of weighted links. The set of key aspects of ANN's is:

The activation state yk of each unit, corresponding to the output of  units. connections between  units. In general, each connection is defined by the weight wjk . This determines the effect of the signal on unit j  on unit k.  Propagation rule that determines the effective input sk of the unit from the external  input. Activation function Fk that determines the new activation level  based on the valid input sk (t) and the current activation yk (t) (ie update).[6][7][8]

 External input of each unit (also called bias or offset) θk.

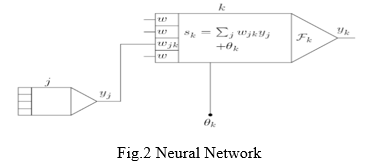
The figure above depicts the basic structure of an artificial neural network and its different components. For the purpose of this project, we construct three neural networks acting as sender, receiver and adversary respectively[6][7][8]. This proposed model, for the purpose of demonstration, includes four layers that make the structure of the convolutional neural networks[4].

???????C.  Convolutional Neural Networks

A Convolutional Neural Network (ConvNet/CNN) is a Deep Learning system that can take an input image, assign relevance (learnable weights and biases) to various aspects/objects in the image, and distinguish between them. When compared to other classification methods, the amount of pre-processing required by a ConvNet is significantly less. While basic approaches require hand-engineering of filters, ConvNets can learn these filters/characteristics with enough training.

CNN encryption's robustness against crypto assaults was not examined, because it is beyond the scope of this research. The final results show how well a particular neural network may be used for symmetric cryptography[11]. For the purpose of demonstration in this context, there are three neural networks. They are as follows:

1. Alice: Assuming that the sending or initiating network is Alice, the generation of the dataset is done in this neural network. A  uniform random generator is implemented for the said generation of the dataset. This stage produces two strings of equal length: the plaintext or message and its associated key. These strings of n-bit each are then passed over to a fully connected layer of this network. The next step for this network is to convert the message and key into a 2n-bit vector, which is then passed to the fully connected layer. It takes in 2n bits and produces a n bit output. This is then passed through a series of sigmoid convolutional layers. At last, the output of the sigmoid layers is then passed to a non-linear tanh layer which scales it to n-bits within the range of -1 to 1 as required.[10]

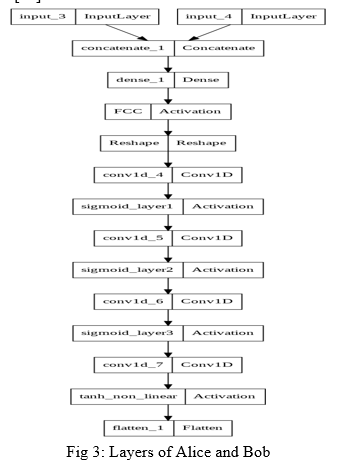
The purpose of each layer is studied later on in this paper.

2. Bob: Consider Bob as the neural network as the receiver of the message. The architecture of Bob is an exact replica of Alice’s. It consists of a fully connected layer, followed by three sigmoid convolutional layers and a non-linear tanh layer. The input to Bob, however, is the n-bit cipher text generated by the sender, in this case Alice, and the key used for the symmetric encryption. All layers perform the same operation as Alice and the output produced is the deciphered text that is the same as the one that was the input to Alice. This process concludes the last stage of symmetric encryption.[10]

3. Eve: In the scenario in consideration, Eve is the adversary, performing a man-in-middle attack.Traditionally, a man-in-the-middle would be able to view messages in transit by eavesdropping through the network. By using machine learning, the neural networks are able to learn crypto-operations and thus eliminates the need for exchanging keys with every message. Here, the architecture of the adversary networks is the same as the others. The inputs to this ANN, however, is only the ciphertext (an identity string is also passed along with the cipher text). This ANN attempts to crack the ciphertext without the use of the secret key known only to Alice and Bob. The primary purpose of this is to test the strength and reliability of using ANNs for symmetric encryption while saving human effort.[10]

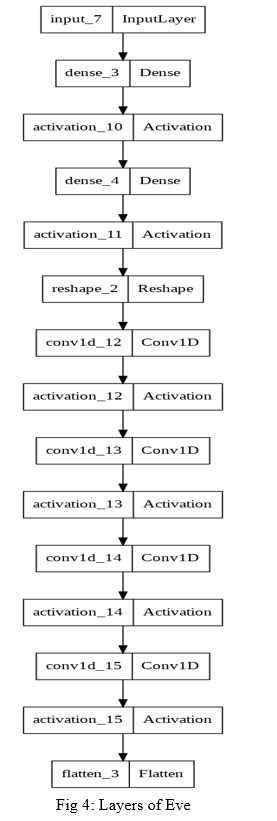
???????D. Proposed Neural Network Architecture

The proposed architecture of each ANN consists of four layers. They are as follows:

1. Fully Connected Layer: FCNNs are a sort of artificial neural network in which all of the nodes, or neurons, in one layer are connected to the neurons in the following layer. While this type of technique is often used to process certain types of data, it has certain limitations when it comes to image identification and classification. Such networks require a lot of processing power and are prone to overfitting. When such networks are also 'deep,' that is, when there are multiple layers of nodes or neurons, they can be very difficult to comprehend for humans.

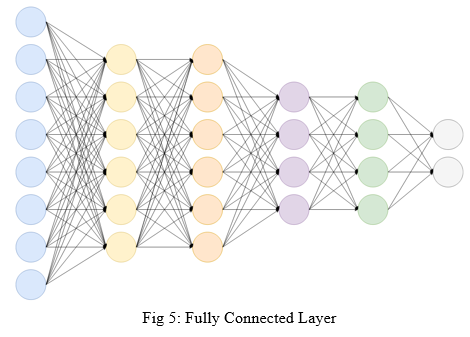
2. Sigmoid Layer: The sigmoid function is a type of logistic function that is commonly symbolised by the  o(x) or sig (x). It is provided by:

σ(x) = 1/(1+exp(-x))

In neural networks, the sigmoid function is utilized as an activation function. An activation function is used to pass a weighted sum of inputs through, and the output is used as an input to the following layer. When a neuron's activation function is a sigmoid function, the output of this unit will always be between 0 and 1. The output of this unit would also be a nonlinear function of the weighted sum of inputs, as the sigmoid is a nonlinear function. A sigmoid unit is a type of neuron that uses a sigmoid function as an activation function[12].

3. Tanh Layer: The Tanh (also "tanh" and "TanH") function is another name for the hyperbolic tangent activation function. It resembles the sigmoid activation function in appearance and even has the same S-shape. The function accepts any real value as input and returns a value between -1 and 1. The larger the input (more positive), the closer the output to 1.0, and the smaller the input (more negative), the closer the output to -1.0.

This is how the Tanh activation function is calculated:

(e^x – e^-x) / (e^x + e^-x)

Where e is the base of the natural logarithm and is a mathematical constant[13].

???????E.  Encrypting and Decrypting Images

The model proposed above works only for text messages. In order to work with files and media content like images, this proposes a combined implementation of chaos maps and the model proposed above. Chaotic theory is a branch of mathematics that studies the dynamic behavior of natural and manmade systems that are affected by initial conditions such as weather, climate, and road traffic. It can be investigated using a chaotic mathematical model, as well as recurrence plots and Poincare maps. Emerging technologies such as neurology, cardiology, control and circuit theory, weather prediction, and others use chaos theory. Chaos is defined as "when the present determines the future, yet the approximate present cannot approximate the future." In chaos, even little changes in the original conditions can result in a sequence that is completely unrelated. For our purpose we have used logistic chaotic maps.[14]

1. Logistic Maps

Mathematically, the logistic map is represented using the equation

      f (x) = rx(1 − x)

      xn+1 = f (xn ) …(1)[14].

Here, xn  depicts the chaotic sequence ranging between  0 and 1 as illustrated in Figure 5.

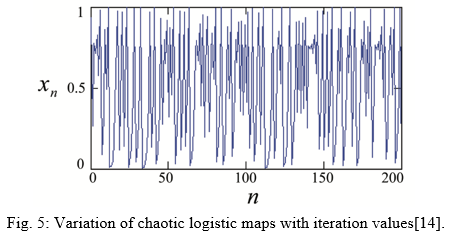
Initially, the map is in the xn=0 = x0 ∈[0,1] state. The variable r takes a value between 0 and 4.When r is between 0 and 1, xn = 0 regardless of the beginning conditions x0. When r is between 1 and 3, the value of xn stabilizes at (r 1) r, regardless of the initial conditions x0. When r is between 3 and 1+ 6 (about 3.45), the value of xn oscillates between two values for as long as r is between 3 and 1+ 6 (roughly 3.45)[14]. The value of xn oscillates between four values forever when r is between 3.45 and 3.54 (roughly). The value of xn oscillates between 8 values when r is somewhat larger than r, then 16, 32, and so on. The commencement of chaos occurs at roughly 3.57 r, at the end of the period doubling cascade[14]. Small changes in the starting state produce significantly different effects over time in this region, which is a key feature of chaos. Beyond 3.57, the behavior is chaotic, but there are isolated values of r that appear to be non-chaotic; these are commonly referred to as islands of stability.[14].The logistic map is a one-dimensional discrete-time map with an astonishing level of complexity despite its formal simplicity. It was historically one of the most important and archetypal systems in the early days of deterministic chaos study[15].

2. Image Encryption

There are three major processes in the encryption algorithm. The chaotic sequences are generated in the first stage. To create the requisite encrypted image, the second stage confused the pixel values, and the third step shuffled the pixel position. Let f be a picture with the dimensions M N. The pixel of f is represented by f(i,j), where i and j are in the range of 1<=i<=M and 1<=j<=N. The grey value at the pixel position (i, j) of the picture f is now denoted by f(i,j). The logistic map's initial condition is derived from a 256-bit (32-character) secret key written in ASCII as K = K1K2 K3......K32 (Ki signifies the 8-bit key character in the i-th key position).[14]

The step by step procedure for logistic encryption using Chaos Maps is as follows[14]:

Step 1: Convert the picture of size M N pixels into an array of P = P,P,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L,P,L Then, using the mod operation, transform the pixel values to an unsigned integer in the range of 0 to 255.The initial values of the chaos map is recalculated after every pixel encryption based on the previous encryption value as well as the key value.

Step 2: With the initial condition x0 and the parameter r = 3.999, generate n number of chaotic sequences xi ={x1,x2,x3,L,xn} in the range 0 to 1 using the logistic map mentioned in Eq. (1). Then, using the mod operation, turn xi into an unsigned integer in the range of 0 to 255.

Step 3: To confuse iii the pixel value, generate the sequence C = P x. The bitwise XOR operation is indicated by the symbol.

Step 4: To get the image f′, convert Ci = {C1,C2,C3,L,Cn} to an array of size MN. Then, to get X, add one to the unsigned integer sequence xi = {x1, x2, x3,L, xn} and convert it to an array of size M N.

Step 5: Finally, perform the pixel shuffling procedures below to obtain the needed encrypted image f. The values of j and k range from 1 to 255. The sign indicates that the values of two pixel positions of f ′ are swapped.

f′(X(j,j),k)⇔ f′(X(j+1,j+1),k)

f′(k,X(j,j))⇔ f′(k,X(j+1,j+1)). (4)

The final encrypted image is now f.

3. Image Decryption

The process of decrypting an image is the inverse of encryption.

4. Proposed Methodology for Image-based Cryptography:

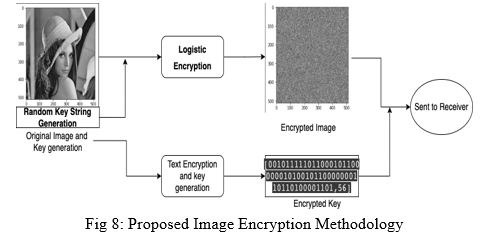
For the purpose of implementing image encryption in our demonstration, we use logistic encryption with key mixing. The generation of the chaos sequence is according to the steps mentioned above but each time a new sequence is generated, it is done with respect to the previous sequence and the key.

The key required for logistic encryption is a string in which only a fixed number of characters are implemented for the purpose of cryptography. This key is then encrypted using the ANN for encryption, in this case Alice, and thus the encrypted key along with the cipher image is transmitted.

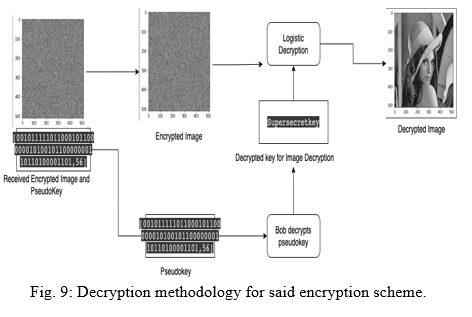
The process of decryption is the reverse of the above process. The encrypted key is first decrypted using the decryption ANN model, in this case Bob. On obtaining the key for image decryption, the “plain” image is then obtained from the encrypted image.

???????F. Advantages

If successfully implemented, this method will have the following advantages:

1. A large number of attackers have been trained, and each new time step  is multiplied to cover the possible internal representation of  the current output.
2. The dynamics of a successful attacker precedes, so the attacker stays while the unsuccessful attacker leaves. A Probabilistic attack in which an attacker attempts to track the probability of each weighting element by calculating the  local field distribution for each input and using  publicly known outputs.
3. As mentioned in point 2 on the learning concept that  weight adjustment is done by accident, this randomization is unknown to the attacker, so these ideas lead to a very distant adjustment range.
4. The need for sharing the secret key every time a message is sent and received (though this method is implemented in some deprecated systems) is eliminated.
5. Once the sender and receiver networks are in a stable synchronization, the need for sharing the key is eliminated as the network itself acts as a key.

???????G. Limitations

1. As it involves machine learning, a lot of time is spent in training the models, which is saved in the traditional Diffe-Hillman algorithms.
2. The limitations of this type of system are minor, but potentially important. This is effectively a private key system where the key is the weight and architecture of the network. Breaking the weights and architecture makes encryption easier. However,  encryption and decryption require both weight and architecture. Knowing  one or the other is not enough to break it.
3. The advantage of this system is that it seems very difficult to break through without knowledge of the methodology behind it.
4. Due to its implementation being through machine learning, it is tolerant towards noise. Most messages cannot be modified by even a single bit with standard encryption schemes. A neural network-based system  allows the encoded message to be varied and still  accurate.

???????H.  Future Possibilities

As huge advances are observed in the field of big data and machine learning, it is obvious that there will be practical implementations of the proposed model with a lot of tweaks and improvements. Furthermore, this paper only discusses symmetric encryption using machine learning and ANNs. Even stronger and reliable are asymmetric encryption algorithms like RSA, etc. which are yet to have an implementation through machine learning. As predicted with symmetric encryption, it is no longer a point to ponder upon that ANNs will supersede the traditional cryptographic functions, provided there is availability of the huge pool of resources and computing power required to do the same. As of writing this paper, there are a few systems capable of performing neural cryptographic operations but steady advantages are being made at a never-seen-before pace in computing power and high performance computing. If it is successfully implemented and made feasible for everyday applications, a drastic decrease in man-in-the-middle attacks will be imminent.

References

[1] Grossi, Enzo & Buscema, Massimo. (2008). Introduction to artificial neural networks. European journal of gastroenterology & hepatology. 19. 1046-54. 10.1097/MEG.0b013e3282f198a0. [2] Zupan, Jure. (1994). Introduction to Artificial Neural Network (ANN) Methods: What They Are and How to Use Them. Acta Chimica Slovenica. 41. [3] T. Dong and T. Huang, \"Neural Cryptography Based on Complex-Valued Neural Network,\" in IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 11, pp. 4999-5004, Nov. 2020, doi: 10.1109/TNNLS.2019.2955165. [4] Chandra, Sourabh & Bhattacharyya, Siddhartha & Paira, Smita & Alam, Sk. (2014). A Study and Analysis on Symmetric Cryptography. 10.1109/ICSEMR.2014.7043664. K. Elissa. [5] O\'Shea, Keiron & Nash, Ryan. (2015). An Introduction to Convolutional Neural Networks. ArXiv e-prints. [6] Volna, Eva & Kotyrba, Martin & Kocian, Vaclav & Janosek, Michal. (2012). Cryptography Based On Neural Network. 10.7148/2012-0386-0391. [7] Sooksatra, Korn & Rivas, Pablo. (2020). A Review of Machine Learning and Cryptography Applications. 591-597. 10.1109/CSCI51800.2020.00105. [8] Kalsi, Shruti & Kaur, Harleen & Chang, Victor. (2017). DNA Cryptography and Deep Learning using Genetic Algorithm with NW algorithm for Key Generation. Journal of Medical Systems. 42. 17. 10.1007/s10916-017-0851-z. [9] P. P. Hadke and S. G. Kale, \"Use of Neural Networks in cryptography: A review,\" 2016 World Conference on Futuristic Trends in Research and Innovation for Social Welfare (Startup Conclave), 2016, pp. 1-4, doi: 10.1109/STARTUP.2016.7583925. [10] T. Kim, T. Y. Youn and D. Choi, \"Deep Neural Networks Based Key Concealment Scheme,\" in IEEE Access, vol. 8, pp. 204214-204225, 2020, doi: 10.1109/ACCESS.2020.3036650. [11] R. Forgá? and M. O?kay, \"Contribution to Symmetric Cryptography by Convolutional Neural Networks,\" 2019 Communication and Information Technologies (KIT), 2019, pp. 1-6, doi: 10.23919/KIT.2019.8883490. [12] https://machinelearningmastery.com/a-gentle-introduction-to-sigmoid-function/ [13] https://machinelearningmastery.com/choose-an-activation-function-for-deep-learning/ [14] Mandal, Mrinal & Dutta Banik, Gourab & Chattopadhyay, Debasish & Nandi, Debashis. (2012). An Image Encryption Process based on Chaotic Logistic Map. IETE Tech. Rev.. 29. 395-404. 10.4103/0256-4602.103173. [15] https://www.complexity-explorables.org/flongs/logistic/

Copyright

Copyright © 2022 Dr. Amol Dhakne, Prasann Shimpi, Sanket Halake, Shivam Dharmshetti, Shashank Singh. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.