Numerical Investigation of Radiation Effects on MHD Convective Heat and Mass Transfer Flow Past a Semi-Infinite Vertical Moving Porous Plate in the Presence of Chemical Reaction

Abstract

The numerical solutions for heat and mass transfer by laminar flow of a Newtonian, viscous, electrically conducting and heat generation/absorbing fluid on a continuously vertical permeable surface in the presence of a radiation, a first-order homogeneous chemical reaction and the mass flux are considered. The plate is assumed to move with a constant velocity in the direction of fluid flow. A uniform magnetic field acts perpendicular to the porous surface, which absorbs the fluid with a suction velocity varying with time. The Equations of continuity, linear momentum, energy and diffusion, which govern the flow field, are solved by using a Finite Element Method. The results of the velocity, temperature, concentration, skin- friction, Nusselt number and Sherwood number has been discussed for variations in the governing parameters.

Introduction

I. INTRODUCTION

Heat as well as mass conversion issues combined with a chemical reaction are of significance in several procedures and have, consequently, conventional a substantial amount of awareness in latest years. In strategies, for instance, drying, dissemination at the surface of a stream organization, Energy exchange a wet cooling tower and the stream in a wilderness cooler, heat and mass exchange occur at the similar time. The potential usages of this stream can be seen in several industries. For instance, in the control industry, amongst the strategies for producing electric power is one in which electrical Energy is separated straightway from a moving conducting fluid. In this article especially keen on situations in which dissemination and chemical reaction occur at generally a similar velocity. At the point when diffusion is a lot quicker than a chemical reaction, at that point just chemical components impact the chemical reaction rate. At the point when diffusion isn't significantly quicker than reaction, the diffusion and kinetics interface to convey inside and out various effects. The investigation of heat production ingestion impacts in moving liquids is significant on account of a few physical issues, for example, liquids experiencing a heat liberated or heat absorbed chemical reaction. Because of the quick development of electronic innovation, powerful refrigerating of electronic gear has develop justified and refrigerating of electronic hardware ranges from singular transistors to centralized server PCs and from Energy providers to phone switch boards and thermal dissemination produce isotopes partition in the combination between gases through particularly light atomic weight (H2 and He) and average sub-atomic weight.

Chambre and Young [1] examined a one-order chemical reaction in the territory of a horizontal plate. Hydromagnetic free convection flows through Porous medium between two coordinate plates were introduced by Rapits et.al. [2]. Helmy [3] explained an unsteady 2-D laminar free convection stream of an in-compressible, electrically directing (Newtonian or polar) fluid through a porous strata boundaryed through the infinite vertical plane surface of stable temperature. D. DastagiriBabu et al. [4] contemplated heat and mass exchange on unsteady MHD free convection pivoting flow through porous strata over an infinite vertical plate with hall impacts. Dekha et al. [5] studied the impact of the one-order homogeneous chemical reaction on the procedure of unsteady stream past a vertical plate with study heat and mass exchange. As of late, Ramana Reddy et al. [6] have inspected the mass transfer and radiation impacts of unsteady MHD free convective fluid flow embedded in Porous medium with heat production/absorption.

The two-dimensional unsteady free convection along with mass transfer flow of an incompressible viscous dissipative as well as electrically directing fluid past an infinite vertical permeable plate were investigated by Gregantopoulos et al. [7]. Gribben [8] introduced the boundary-layer flow over a semi-infinite plate with an adjusted magnetic field within the sight of a pressure gradiant. He acquired answers for huge and little magnetic Prandtl number utilizing the strategy for coordinated asymptotic development. For some modern applications, for example, glass creation and heater structure, and in space innovation applications, for example, cosmical flight optimal design rocket, drive frameworks, plasma material science and rocket ship re-entry aero-thermodynamics that works at higher temperatures, radiation impacts must be huge considerable. Along these lines, the various authors [9]-[16] talked about.

There was a renewed enthusiasm for examining magnetohydrodynamic (MHD) stream and heat exchange in permeable as well as non-permeable media because of the impact of the magnetic fields on the boundary layer stream control and on the presentation of various frameworks utilizing electrically conducting liquids, talked by Numerous authors [17]-[19] 

The examination of heat production or assimilation effects in moving fluids is critical due to not many physical issues, for examples, fluids experiencing heat liberated or heat absorbed chemical reactions. 

Conceivable heat production assets may change the temperature dissemination and subsequently, the molecule statement rate in nuclear reactors, electric chips and semi-conductor wafers. The Influence of the chemical reaction and radiation absorption on free convection flow via porous strata with uneven suction within the sight of uniform magnetic field was concentrated by Sudheer Babu and Satyanarayana [20]. The impacts of chemical reaction, thermophoresis and also uneven thickness on stable hydromagnetic stream along with heat as well as mass exchange over a plane plate in the occurrence of heat production/assimilation were investigated by Seddeek [21]. The MHD free convection fluid flows long-ago a semi-infinite vertical porous plate by means of heat assimilation and chemical reaction were investigated by Ramana Reddy G.V et al. [22]. Radiation effects on MHD convective heat and mass transfer flow past a semi-infinite vertical moving porous plate in the presence of chemical reaction were investigated by Raju .V.N et.al. [23]. Chemical Reaction and Heat Source effects on MHD Free Convective Flow over a linearly Accelerated Moving Vertical Porous plate were investigated by Sweta Matta et.al [24].

Despite the earlier studies, there has been little interest in the transient MHD free convection heat and mass exchange for a heat production/assimilation through radiation assimilation in the occurrence of a reacting mass on a in?nite porous plate. For this reason, the main purpose of this part exists to study the impacts of thermal radiation, chemical reaction, and heat source/sink parameter of an electrically conducting liquid past an in?nite vertical permeable plate focused too unpredictable suction. The plate is considered to be installed in a uniform Porous medium and travels with a fixed velocity in the stream direction within the sight of a crosswise magnetic field. The temperature is high; changing drastically from time to time. With the help of a finite element method in this problem we are going to solve the equations of continuity, linear momentum, Energy and diffusion, which govern the flow field. The conduct of the velocity, temperature, concentration, Cf, Nu and Sh has been examined for varieties in the governing boundaries.

II. MATHEMATICAL FORMULATION

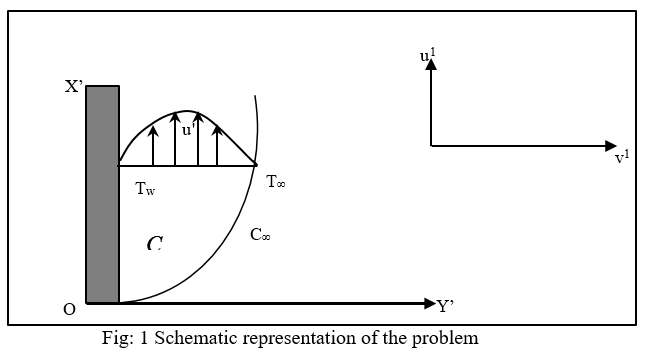
Consider the unsteady two-dimensional stream of a laminar, viscous, electrically directing along with exothermic liquid past a semi-infinite vertical penetrable moving plate surrounded in a uniform Porous medium exposed in the direction of a uniform crosswise magnetic field within the sight of thermal also concentration buoyancy impacts. It is expected with the intention that there is no applied voltage which suggests the non-attendance of an electrical field.

The liquid properties believed to be steady aside from that the influence of density variation along with temperature has been viewed as just in the body-force term. The concentration of diffusing mass is little in contrast with new chemical mass, the grouping of mass a long way from the wall, is infinitesimally little and thus the Soret and Dufour impacts are disregarded. At this time the chemical reaction is occurring in the stream as well as all thermo physical properties are thought to be steady of the linear momentum equation which is estimated by the Boussinesq estimation. Because of the semi-infinite flat surface supposition, the stream variables are functions of as well as the time  as it were. Above these assumptions, the governing equations for the issue assumed in this section depend on the parities of mass, linear momentum, Energy and concentration mass and corresponding equations are as presented below:

Continuity Equation:

Exterior the boundary-layer, equation (2) gives

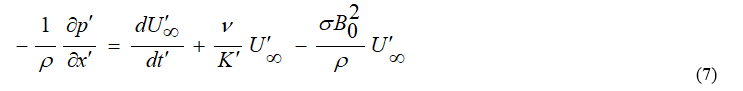
By utilizing the Rosseland dispersion approximation as well as subsequent among different specialists, is the radiative heat ?ux and it is presented as

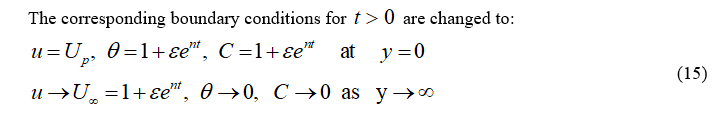
III. SOLUTION OF THE PROBLEM:

The above sets of coupled non-linear partial differential equations subject to the boundary conditions are solved by Finite Element Technique. The fundamental steps comprising the method are as follows.

1. Step 1: Discretization of the domain into elements.
2. Step 2: Derivation of the element equations.
3. Step 3: Assembly of element equations.
4. Step 4: Imposition of Boundary Conditions.
5. Step 5: Solution of the assembled equations.

The problem heat and mass transfer by laminar flow of a Newtonian, viscous, electrically conducting and heat generation/absorbing fluid on a continuously vertical permeable surface in the presence of a radiation, a first-order homogeneous chemical reaction and the mass flux presented in this study. Numerical solutions have been carried out for the non-dimensional Temperature Concentration C, velocity (u) keeping the other parameters of the problem fixed. Numerical calculations of these results are presented graphically in the figures from (2) to (17). These results show the effect of different parameters on the velocity, temperature distribution and concentration profiles at the wall. To find out the solution of this problem, we have placed an infinite vertical plate in a finite length in the flow. Hence, we solve the entire problem in a finite boundary.

The skin-friction, Sherwood number as well as Nusselt number are significant objective parameters designed for this form of boundary-layer flow

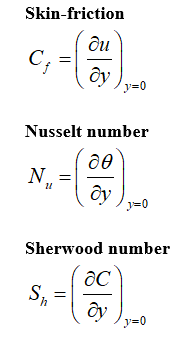
IV. RESULT AND DISCUSSION

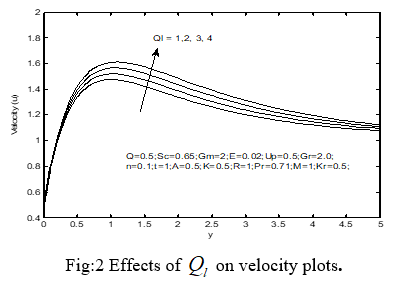
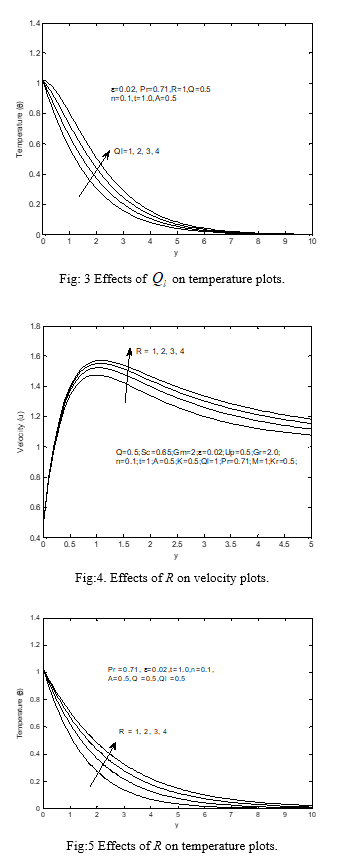
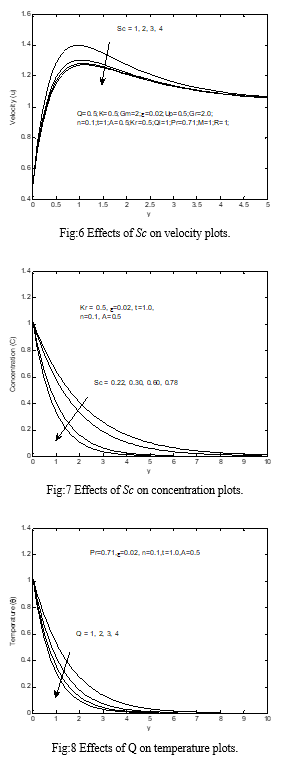
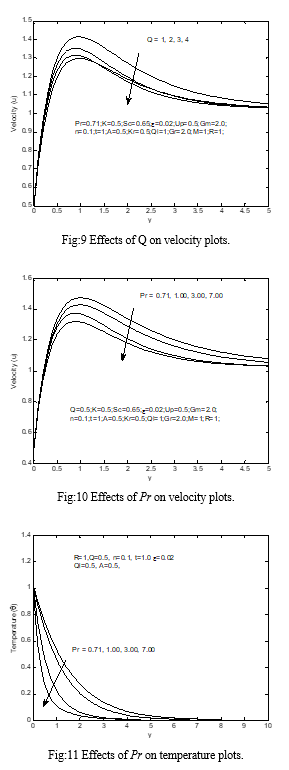
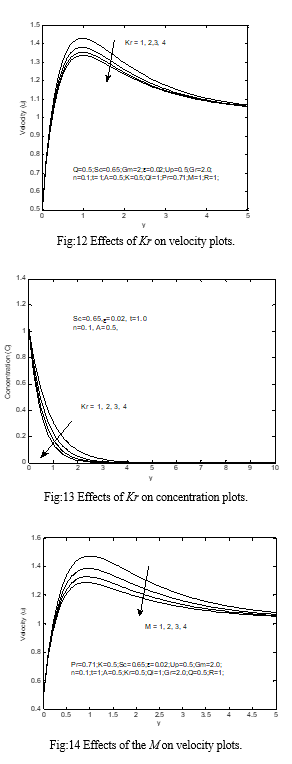
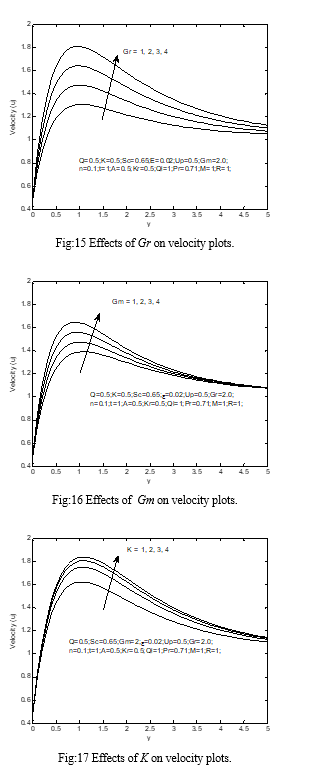
The impact of the magnetic field on velocity plots in the boundary-layer is delineated in the impact of expanding the estimation of the  on the velocity is demonstrated Fig: 2 here seen in this figure expanding the estimation of the absorption of the radiation parameter because of the expansion in the buoyancy force quickens the stream rate. The impact of assimilation of the radiation boundary on the temperature profile is appeared in Fig: 3 The effect of the compound of radiation can be observed from this figure enhance the heat in the boundary-layer like the radiated heat is wrapped up through the liquid, which enhences the temperature of the liquid near the permeable boundary-layer and its effect decreases far away from the boundary-layer. Fig: 4 clarify the velocity plots for various estimations of the R, observably as R increments the extreme estimations of the velocity will in common increment. Fig: 5 demonstrate the temperature plots for various estimations of the R, plainly as R has increment the extreme estimations of the temperature will in general increment. Fig: 6 show the effects of Sc on velocity plots. When the Sc has increment the velocity field declines. This decreases the fluid velocity due to buoyancy effects. The decreases in the velocity plots are joined through the instantaneous decreases in the velocity boundary-layers. Fig: 7 illustrate the impacts of Sc on the concentration plots. As the Sc has increment the concentration diminishes. Fig: 8 are designed to represent the variety of temperature plots against y for various estimations of Q by solving other physical parameters. From this figure, it is observed that temperature diminishes with increment in the Q since when the heat is wrapped up; the buoyancy force diminishes the heat plots. The effect of intensifying the estimate the Q is to diminish the boundary-layer as appeared in Fig: 9 with Q, the buoyancy and stream rate reduce which in turn dimishes the velocity plots. Fig: 10 illustrate the velocity plots for various estimations of Pr. The mathematical outcomes display that the impact of increasing estimations of Pr outcomes in diminishing velocity. Fig: 11 delineate the temperature plots for various estimations of Pr. It are seen that the temperature decline as a Pr has increment. The explanation is that little estimations of Pr are alike to increment in the warm conductivity of the fluid and hence heat can diffuse left from the heated surface more quickly for higher estimations of Pr. Henceforth on account of littler Pr the thermal boundary-layer is thicker as well as the rate of heat transfer is diminished. Fig: 14 explained that the velocity begins from lowest amount estimation at the surface and increment till it achieves the pinnacle estimation and afterward begins diminishing until it approaches to the lowest amount estimation toward the end of the boundary-layer for all the estimations of the M. It is fascinating to note down that the impact of the M is to diminish the estimation of the velocity plots through the boundary-layer. This sort of opposing force slows down the fluid velocity as appeared in this figure. Figs: 12 and 13 shows the velocity and concentration dissemination u against y for various estimations of Kr. At this time seen that the velocity and concentration decline with enhances Kr. For the instance of various estimations of thermal Gr, the velocity plots in the boundary-layer are appeared in Fig: 15 it is seen that an increment in Gr show the way to an increment in the estimations of velocity because of upgrade in buoyancy force. At this time, the positive evaluation of Gr relate to refrigeration of the surface. Fig: 16 presents complicated velocity plots in the boundary-layer for various estimations of the Gm, while every single additional parameter are set aside at some predetermined estimations. The velocity distribution achieves a particular most extreme assessment in the neighborhood of the plate surface and afterward declines appropriately to move toward the free stream esteem. As expected, the liquid velocity increments and the extreme value more distinctive due to increment in the concentration buoyancy effects represented by Gm. This is clear that in the increment in the estimation of u as Gm increments. Fig: 17 display the velocity plots for various estimations of the K, obviously, as K increments the extreme estimations of the velocity will in general increment.

Conclusion

The numerical outcomes for mass and heat transfer flow a Newtonian, viscous, heat generation/absorbing alongside electrically conducting liquid on a continuous vertical surface with pores, radiation and with a one order homogeneous chemical reaction also the mass flux has been examined and the prevailing equations for the velocity fluid, temperature as well as concentration by utilizing finite element method in relations of dimensionless parameters. Following conclusions are given the brief results of the present study 1) The velocity enhances with increases of R, Sc, Gr, Gm, K. 2) The velocity declines with increases of Q, M, . 3) The temperature enhances with increases of R, . 4) The temperature declines with increases of Q, . 5) The concentration enhances with the increases of Sc. 6) The concentration declines with the increases of . A. Nomenclature M signifies magnetic field parameter, K signifies permeability parameter, Gr signifies thermal Grashof number, Gm signifies Solutal Grashof number, Pr signifies Prandtl number, signifies Chemical reaction number, Q signifies heat absorption parameter, signifies absorption of radiation parameter, R signifies thermal radiation parameter, t signifies time, signifies Velocity Components, signifies the thermal temperature, -the speci?c heat, g -the gravitational increment of velocity B. Greek Symbols ? -the ?uid density, -the Darcy permeability’ Sc -Schmidt number, D -the diffusion coefficient -the heat ?ux and are the thermal also concentration extension coefficients ? -the electric conductivity - Dimensionless temperature

References

[1] Chambre, P.L., Young, J.D.; ‘‘On Diffusion of a Chemically Reactive Mass in a Laminar Boundary-layer Flow’’, Physics of Fluids, 1, 1958, 40-54. [2] Raptis, A., Massalas, A., Tzivanidis, G., “Hydromagnetic Free Convection Flow through a Porous Medium Between Two Parallel Plates”, Physics Letter A, 90 (6), 1982, 288-289. [3] Helmy, K.A., “MHD Unsteady Free Convection Flow Past a Vertical Porous Plate”, ZAMM, 78, 1998, 255-270. [4] DastagiriBabu, D., Venkateswarlu, S. and Keshava Reddy, E., “Heat and Mass Transfer on Unsteady MHD Free Convection Rotating Flow through a Porous Strata over an Infinite Vertical Plate with Hall Effects”, AIP Conference Proceedings 1859, 020077, 2017, 1-9. [5] Dekha, R., Das, U.N. and Soundalgekar, V.M., “Effects on Mass Transfer on Flow Past an Impulsively Started Infinite Vertical Plate with Constant Heat Flux and Chemical Reaction”, Forschungim Ingenieurwesen, 60, 1994, 284-309. [6] Ramana Reddy, G.V., Ramana Murthy, Ch.V., Bhaskar Reddy, N., “Mass Transfer and Radiation Effects of Unsteady MHD Free Convective Fluid Flow Embedded in Porous Strata with Heat Production/Absorption”, Journal of Applied Mathematics and Fluid Mechanics, 2(1), 2010, 85—98 [7] Rajkumar, K.V.B., Balamurugan, K.S., Ramana Murthy, Ch.V., Umasenkara Reddy, M., “Chemical Reaction and Viscous Dissipation Effects on MHD free Convective flow Past a Semi-Infinite Moving Vertical Porous Plate with Radiation Absorption”, Global Journal of Pure and Applied Mathematics, 13(12), 2017, 8297-8322. [8] Gribben, R.J., “The Magnetohydrodynamic Boundary-layer in the Presence of a Pressure Gradient”, Proc. Royal. Soc., London, 287(1408), 1965, 123-141. [9] Hossain, M.A., Takhar, H.S., “Radiation Effect on Mixed Convection along a Vertical Plate with Uniform Surface Temperature”, Heat Mass Transfer, 31, 1996, 243-248. [10] Kim, Y.J, and Fedorov, A.G., “Transient Mixed Radiative Convection Flow of a Micro Polar Fluid past a Moving Semi-Infinite Vertical Porous Plate”. International Journal of Heat Mass Transfer, 46(10), 2003, 1751-1758. [11] Ramana Murthy, M.V., SrinivasaRaju, R., AnandRao, J., “Heat and Mass Transfer Effects on MHD Natural Convective Flow past an Infinite Vertical Porous plate with Thermal Radiation and Hall Current”, International Conference on Computational Heat and Mass Transfer-2015, Procedia Engineering, 127, 2015, 1330 – 1337. [12] Mohamed, R.A., “Double Diffusive Convection-Radiation Interaction on Unsteady MHD Flow over a Vertical Moving Porous Plate with Heat Production and Soret Effect was Studied”, Applied Mathematical Scieces, 3(13), 2009, 629-651. [13] Mohamed Abd El-Aziz, Aishah, S. Yahya., “Heat and Mass Transfer of Unsteady Hydromagnetic Free Convection Flow through Porous Strata Past a Vertical Plate with Uniform Surface Heat Flux”, Journal of Theoretical and Applied Mechanics, Sofia, Vol. 47( 3), 2017, 25-58. [14] Muthukumaraswamy, D. R., “Effects of a Chemical Reaction on a Moving Isothermal Surface with Suction”, ActaMechanica 155, 2002, 65-72. [15] Muthukumaraswamy, R., Meenakshisundaram, S., “Theoretical Study of Chemical Reaction Effects on Vertical Oscillating Plate with Variable Temperature”, Theoret. Appl. Mech., 33(3), 2006, 245-257. [16] Muthuraj, R., Srinivas, S., “Fully Developed MHD Flow of a Micro polar and Viscous Fluid in a Vertical Porous Space using HAM”, Int. J. Appl. Mathematics and Mechanics, 6(11), 2010, 55-78. [17] Patil, P.M., Kulkarni, P.S., “Effects of Chemical Reaction on Free Convective Flow of a Polar Fluid through a Porous Strata in the Presence of Internal Heat Production”, Int. J. of Thermal Sciences, 47(8), 2008, 1043-1054. [18] Ramachandra Prasad, V., Bhaskar Reddy, N., “Radiation Effects on an Unsteady MHD Convective Heat and Mass Transfer Flow Past a Semi-Infinite Pertical Permeable Moving Plate Embedded in a Porous Strata”, Journals of Energy Heat and mass transfer,30, 2008, 57-68. [19] Satyanarayana, P.V., Venkataramana, S., “Hall Current Effect on Magneto Hydrodynamics Free-Convection Flow Past a Semi-Infinite Vertical Porous Plate with Mass Transfer”, S.V. University, Ph.D thesis, 2007. [20] SudheerBabu, M. SatyaNarayana, P.V., “Effects of the Chemical Reaction and Radiation Absorption on Free Convection Flow Through Porous Strata with Variable Suction in the Presence of Uniform Magnetic Field”, J.P. Journal of Heat and mass transfer, 3, 2009, 219-234. [21] Seddek, M.A., “Finite-Element Method for the Effects of Chemical Reaction, Variable Viscosity, Thermophoresis and Heat Production/Absorption on a Boundary-Layer Hydro Magnetic Flow with Heat and Mass Transfer Over a Heat Surface”, ActaMechanica, 177, 2005, 1-18. [22] Ramana Reddy, G.V., “MHD Free Convection Fluid Flow Past a Semi-Infinite Vertical Porous Plate with Heat Absorption and Chemical Reaction”, International Journal of Chemical Sciences, 13(1), 2015, 525-540. [23] Raju, V. N., Hemalatha, K., & Babu, V. S., ‘‘Radiation effects on MHD convective heat and mass transfer flow past a semi-infinite vertical moving porous plate in the presence of chemical reaction, international journal of engineering sciences & research technology, 7(8), 2018, 146-161. [24] Sweta Matta, Bala Siddulu Malga, Lasksmi Appidi, P.Pramod kumar, ‘‘Chemical Reaction and Heat Source effects on MHD Free Convective Flow over a linearly Accelerated Moving Vertical Porous plate, Indian Journal of Science and Technology, 14(13), 2021, 1044-1055.

Copyright

Copyright © 2022 Nagaraju Vellanki, Dr. V. Srihari Babu, CH. Srilakshmi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.