Optimization of Heat Transfer Rate in Fins by CAE

Abstract

Overheating and excessive increase in the temperature of the compressors body causes thermal loading on the compressors surfaces. The life of the compressor mainly depends upon the abrupt change in the thermal stresses and the pressure stress induced in the body. The life of the compressor can be successfully improved and optimized by working on the compressor body. Specifically speaking the compressors fin areas is the heat affected area. Change in small cross section area can significantly change the convective heat transfer. This project report focuses on providing economical methods which are optimized and also easily implementable solutions in the existing manufacturing setup. The above techniques are implemented on compressor head body. All possible attempts are made to change the cross section and the shape of the heat transfer areas so that maximized heat transfer reached in the operating process. The implementation of the optimize techniques is carried out by analyzing different cross sections such as straight, trapezoidal and parabolic. The scope of revising the strategies ultimately helps to increase productivity, efficiency, pointing to increase the profit. The only aim to propose the solution is to optimize the heat transfer rate by the change in the design.

Introduction

I.  INTRODUCTION

A. Compressor- Heat Transfer Medium

Compressor becomes almost an integral part of the mechanical industry and many other commercial applications. The compressed air is used in many other applications such as the Mechatronics system where high amount of high pressurized air is required. The electrical energy is not only used for increasing the pressure of the fluid or the gas, but there is simultaneous increase of the temperature of the fluid as well. In most case the heat is removed by some passive means since the temperature is not high as the IC engines. Still the increase of the temperature is quite enough for creating the temperature patterns which increases the thermal loading and the thermal stresses. This generated temperature stresses as well as the flow induced stresses are quite enough for the defining the overall effective operating life of the compressor.

This removal of the heat transfer becomes an essential issue while designing the compressor body. The distribution of the heat is totally taken care by the fin design that is present on the outer surface of the compressor body. The only aim that is related while designing is to increase the maximum surface area so that the heat is dissipated through the fins. The convective heat transfer is enhanced by addition of the fins. Similarly if the change in the flow from laminar to turbulent is focused in that scenario there is effective mixing of the hot and cold air removes heat quickly. [1]

The CFD approach has almost replaced the experimental technique method which saves the time and the cost involved.  Figure 1.1 shows the fin design of an automobile component.

B. Aluminium Material

Selecting Aluminium material is the best option due to it physical characteristics. Aluminium alloys that are use for die casting process have a specific gravity of approximately 2.7 g/cc, placing them among the lightweight structural metals. Six major elements constitute the die cast aluminium alloy system: silicon, copper, magnesium, iron, manganese, and zinc. Each element affects the alloy both independently and interactively. Different types of material that are generally used for die casting process are presented in Appendix A. [2-7]

C. Statement of the Problem

The designs of the fins that are present of the any mechanical component for the purpose of the heat dissipation are very important as far as the life of the fin body is concerned. The components where the fins are used are not subjected electrical energy that increase the pressure but also increase the temperature of the respective body. This inculcation of the heat as well as the temperature is responsible for creating different types of thermal loading which is responsible for defining the life span of the fin body.

The problem identified for dissertation work is to concentre on the designing and manufacturing of the compressor head having fins. Optimizing of different design parameters is proposed to increase the life of the compressor head body. Parameters such as the thickness of the fin, length, cross section of the fin, the pitch between adjacent fins are some parameter which is closely assessed for increasing span by improving the thermal conditions of the physical component.

D. Objective of the Study

Following objectives are coin for the die casting of automobile components viz:

1. Increasing the life span of the compressor body.
2. Increase the heat transfer rate through the body.

Finding the various heat transfer rate distribution for the same body by changing the cross section such as rectangle, trapezoidal and parabolic

E. Limitations of the Study

The analysis is done on the compress body having the fixed bore diameter. The diameter can’t be altered since it’s a constraint of the physical assembly. The heat transfer can be enhanced by increasing the diameter of the bore i.e. increasing the physical heat transfer area.

II. LITERATURE REVIEW

A. Introduction

There has been a lot of research done by various people on the design of the fin body which will enhance the heat transfer rate. The various methods which are implemented by designer may be in terms of thickness of the fin, or the profiles cross section of the fin area, creation of special cuts which will increase the area of heat transfer. The Literature reviews presented in this chapter discuss the different and innovative methods of manufacturing of the fin body.

B. Physically Tested fin Model and Design

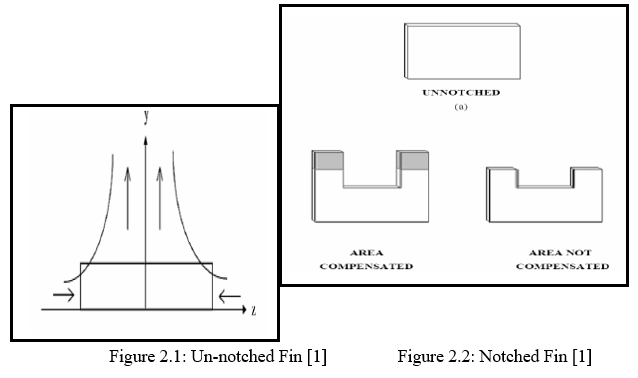
Towards setting up an ideal design, Shivdas Kharche et al. [1] has reported the possible attempts can be made in cross section areas of the fin. The authors have much more focus on the analysis of the rectangular fin. As per author experimental analysis and the theoretical testing of the rectangular fin is made. There are two case analyzed for plotting the optimized heat transfer in case of fins. In case I normal testing is done on a rectangular cross section which is also called as the single flow chimney pattern figure 2.1 shows the details for the same, similarly in case II a notch is made in a rectangular section. The rectangular notch is present at the centre of one of the edges, which will in turn create a “c” section for the analysis figure 2.2 shows the notched fin.                       

The author reveal about the material saying that a lot of work is carried on aluminium material. Hence the above test is carried on copper material which can be used as one of the alternative material for aluminium.

As per the author the best material for fin design is the aluminium and copper. Conclusion can be laid by considering the parameters such as fin spacing, fin height, fin length and the fin temperature difference. The experimental setup is shown in figure 2.3.

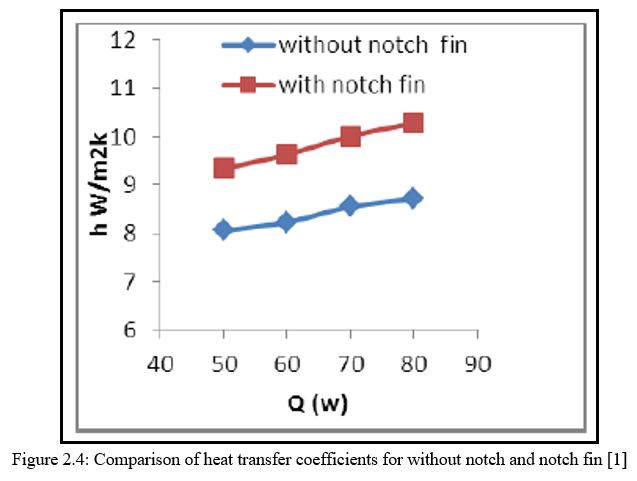
The author finally reveals about the results about the test carried for the above design parameters which are as follows, the heat transfer is increased by increasing the height(H) of the fin and decreasing the length(L) of the fin. H/L ratio is responsible for the increasing the heat transfer rate. Figure 2.4 shows the comparative results for heat transfer coefficients for both processes.

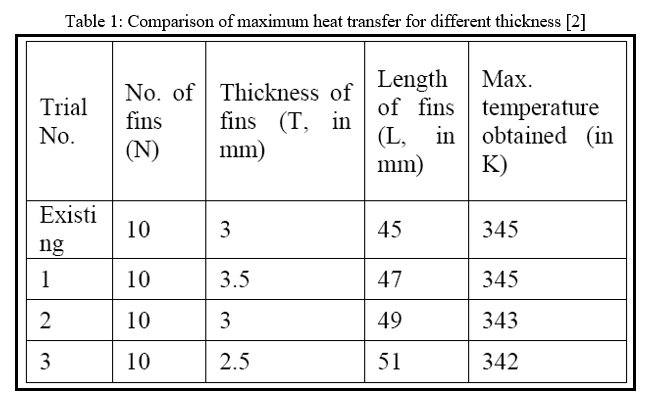
Further P. Raghupati and Dr. Sivakumar [2] explains about thickness to length ratio to be taken for an ideal design for optimization of the heat transfer rate through the compressor body. In the test carried by the author the number of fins in the test are taken are constant. These are 10 in numbers. The alteration for maximum heat transfer is obtained by the change in the thickness to length ratio. Depending on the economical aspect of the material thickness lies between 2-3 mm. Necessary length for maximum heat transfer is found out by physical testing for different lengths.

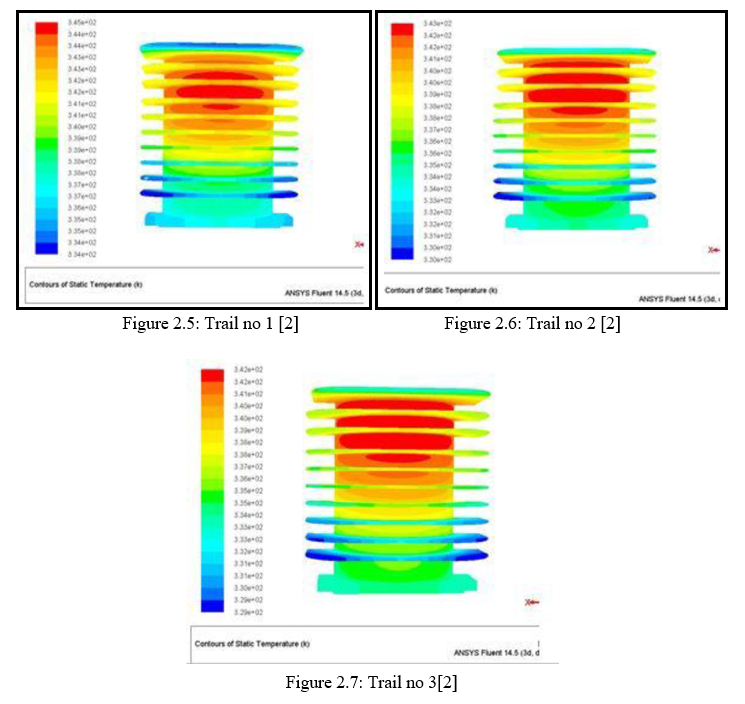
The author carried out 2 tests for 3mm thickness keeping the length of the fins as 45mm and 49 mm respectively. Another test of 3.5mm thickness was carried out on 47mm length. The results shows that temperature difference obtained for 3 mm thickness is 345K and 343K for 45 and 49mm respectively, similarly 345K is obtained for 3.5mm thickness. The results are tabulated in table no 1 [2]. Refer figure 2.5-2.7

Mohammad Mashud et al. [3] have discussed much more on the keeping cylindrical fin as the base fin. Some minor changes are brought in act on the cylindrical profile which will be responsible increase in the heat transfer through the compressor body. The analysis for heat transfer is carried out on a plain cylindrical fin, circular cylindrical fin and threaded cylindrical fin. The diameter of the cylindrical fin is 20mm with a length of 150mm. Convective heat loss reduces sharply as pressure is decreased. It is because as the pressure inside the pressure reduction chamber is reduced, a low-density situation arises. In low-density circumstances the mean free path of the gas molecules is large enough, and as density reduces this distance increases. The larger this distance becomes, the greater the distance required to communicate the temperature of a hot surface to a as in contact with it. This means, it cannot be assumed that the layer or air in the immediate neighbourhood of the surface of the fin will not have the same temperature as the heated surface. This causes a considerable reduction in convective heat transfer coefficient, h [3]. Refer figure 2.8

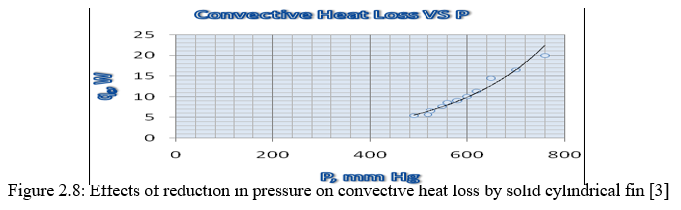
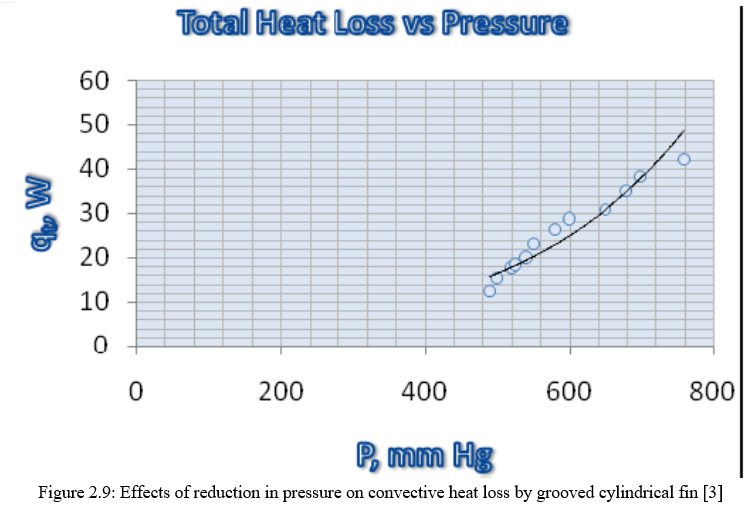
  The effect of pressure reduction on the heat transfer through the cylindrical fin with circular grooves is shown figure 2.9. It is observed that, with the increase of vacuum pressure there is a considerable reduction in heat transfer rate. At atmospheric pressure heat loss is about 42 W. For a pressure of 490mm Hg heat loss is about 12.4, which is 29.52% of the total heat loss corresponding to the atmospheric pressure. From Figure 2.8 it is observed that heat loss due to convection reduces more rapidly with pressure for circular grooved cylindrical fin. The curve obtained from above figure 2.8 has much higher slope than the curve obtained from figure 2.9 for solid cylindrical fin. This indicates higher performance of grooved cylindrical fin than solid cylindrical fin. [3]

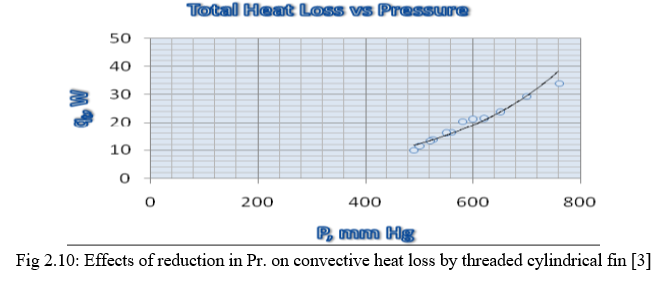
The curves obtained for threaded fin are discussed in figure 2.10 shows the effect of variation of absolute pressure on total heat loss by a threaded cylindrical fin, which includes the effect of convective as well as radiative heat losses. It is observed that, with the increase of vacuum pressure there is a considerable reduction in total heat transfer rate. At atmospheric pressure heat loss is about 33.9 W. For a pressure of 490mm Hg heat loss is about 10, which is 29.49% of the total heat loss corresponding to the atmospheric pressure.

From this experimental study it has been found that the grooved radiating fin loses approximately 1.23 times greater heat per unit area, compared to the threaded pin fin, and 2.17 times greater heat per unit area, compared solid to the solid pin fin at a pressure lower than atmospheric pressure. As pressure decreases heat loss reduces and contribution of radiation heat transfer on total heat loss increases. [3]

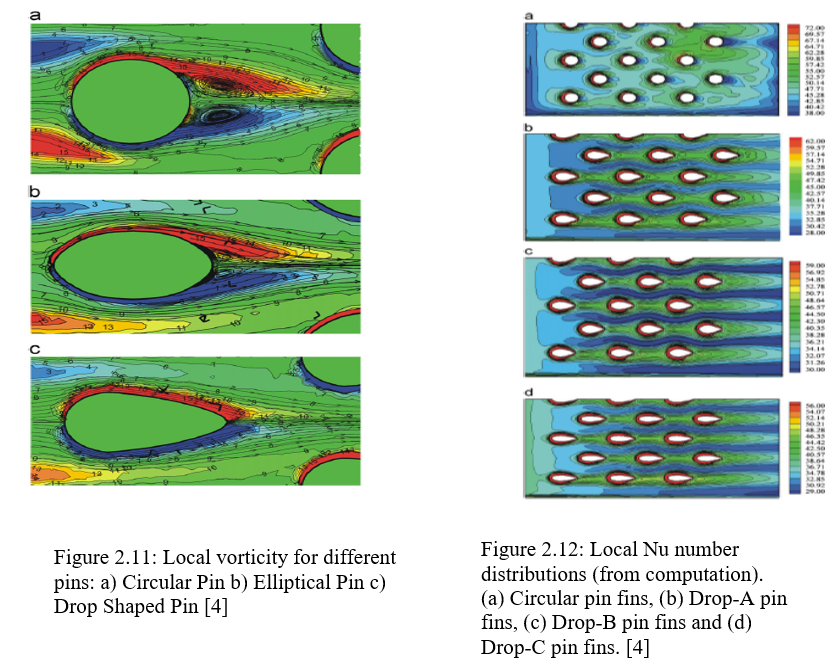
Fengming Wang, Jingzhou Zhang et al. [4] made an experiment setup for acquiring the maximum heat transfer characteristics in a rectangular fin. The test was carried on family of similar cross section such as a circular fin, elliptical fin and dropped shape fin. The diameter of the circular fin is 6mm, the major and minor axis of the ellipse are 4.24mm and 2.12mm respectively. Lastly the dropped fin has 4.6, 4.2 and 3.8 as the minor axis; similarly is having 8.5, 9.2 and 10.1 as the major diameter. The results which were obtained on actual testing were as follows:

1. Flow characteristics
2. Heat transfer characteristics.

The graph shown in figure 2.11 and 2.12 shows the local vorticity for different cross sections. The detailed local vorticity distributions on the mid-height plane of the flow channel for different pins. Two vortical structures dominated the vorticity distribution: horseshoe and wake vortices. The occurrence of these vortical structures depends on the interaction of the primary flow and pin fins. Horse- shoes are formed in the flow around a blunt body and roll up at the pin rim. Wakes are induced by flow separation when the windward flow is exposed to a blunt body and manifests near the trailing edge of a pin. The horseshoe is a considerably smaller structure with a negligible effect on the aerodynamic penalty compared to wake vortices.

Further figure shows the local Nusselt (Nu) number distribution for different pins. Circular pins seemed to have the strongest convective heat transfer intensity among the five cases in the current study. In addition, the windward blockage by a circular pin fin array was maximal for all cases; the flow was forced to follow a more twisted path around the pins, which decreased the pressure drop. Final conclusion can be made as follows, the more streamlined drop-shaped pin fins are better at delaying or suppressing separation when a flow passes through them, which reduces the aerodynamic penalty compared to circular pin fins. Similarly heat transfer characteristics shows that heat transfer enhancement of drop-shaped pin fins is weaker than that of circular pin fins. The reduction in average Nusselt number between the drop-shaped and circular pins was about 24% for drop-A, 26% for drop-B, and 27% for drop-C.

Mehendi Ehteshum et al. [5] has explained the effects of per formation on the rectangular fin body. The aim in making per formation is to increase the area, so that maximum heat transfer can be possible. Table no 2 explains about the detail and different possible construction features made on a rectangular fin.

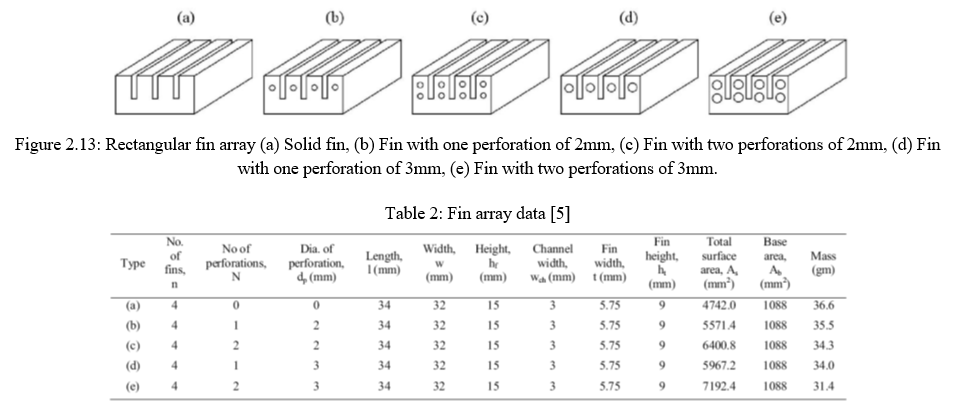
Different combinations are made in rectangular fins so that maximum heat transfer is obtained. This is done by designing cross section as shown in figure 2.13. Figure 2.13a shows the initial basic design of rectangular fin, figure 2.13b shows the hole of diameter 2 made at the centre of the fin, figure 2.13c shows the hole of diameter 2 made at the centre of the fin but there are two rows instead of one. Similarly figure 2.13d and 2.13e are similar to 2.13b and 2.13c having the change in the diameter from 2 mm to 3mm respectively. Table 2 shows the actual parameters of the fin design that are exactly available on the fin area.

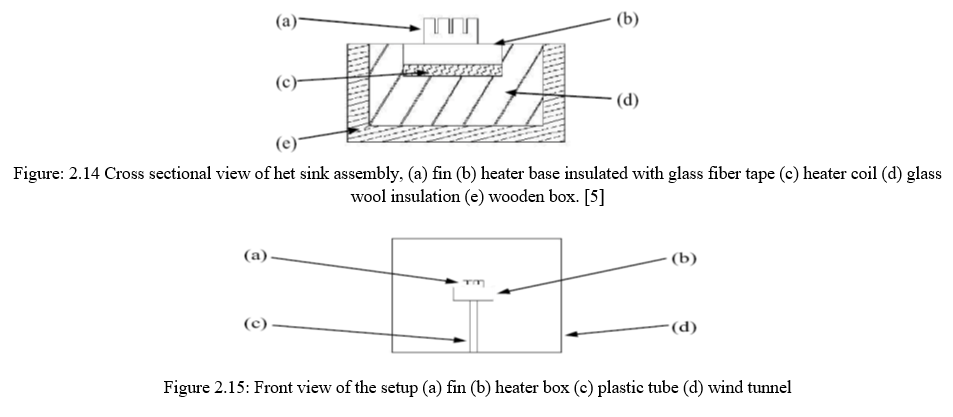
The setup is placed in a wooden box as figure 2.14 and 2.15. The fins are heated by electrical heater insulated by 1.6mm glass-fiber tape with a thermal conductivity of 0.04W/m-K. Further the heater is insulated by glass-wool having a thermal conductivity of 0.04W/m-K. The fins are manufactured from aluminium (Al) block having 23704W/m-K as its thermal conductivity. The bottom surfaces of the heater coil are provided so that the fins can be placed. The whole setup is placed on a plastic tube which stands inside a wind tunnel.

The result that are obtained from the above setup gives relationship between the heat transfer coefficient  and the Nusselt number for different fins corresponding to different Reynolds number(Re) shown in figure 2.16 and 2.17 respectively. The results shown perforated fins have high and effective heat transfer rate as compared to the solid fin, both the efficiency and effectiveness is decreased with increase in air velocity (Re).

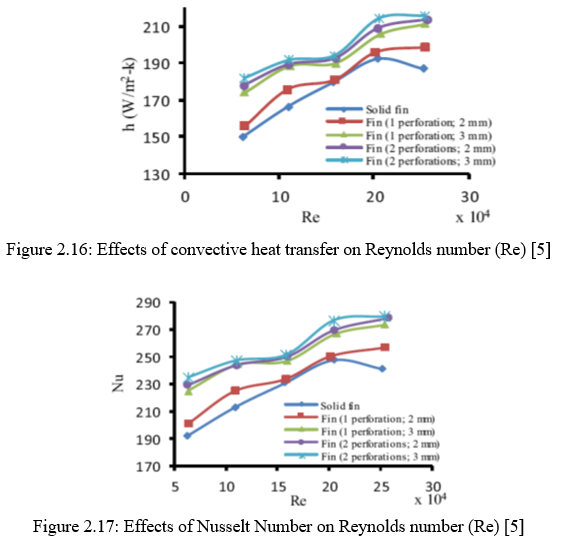
Further the results show that heat transfer coefficient rate is significantly increased with fin having higher diameter over fin having smaller diameter i.e. fin having diameter 3mm has higher heat transfer coefficient than fin having 2mm diameter. Nusselt number which is a dimension less number also shows results on the similar basis as that of the heat transfer coefficient. Figure 2.17 shows the graph of effects of Nusselt number on Reynolds number. Finally to conclude increase in Reynolds number increases both the heat transfer coefficient and Nusselt number as well decreases the thermal resistance. Solid fin has maximum thermal resistance than perforated fin. The value of the thermal resistance decrease as the diameter of the perforation goes on increasing.

S M Wange et al. [6] has again focused on the notch creation which makes an attempt to increase heat transfer, same as explained by Shivdas Kharche et al. [1]

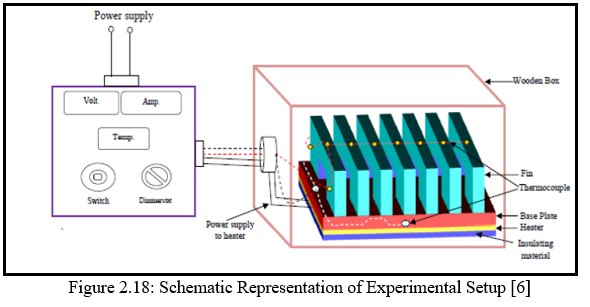
The experimental setup is shown in figure 2.18. The fin array consists of number of fins fixed to the base plate by using aluminum welding operation. Heating coil placed in the base portion of the fin array. The heating coil is fixed in an insulating box. An assembled array is placed in insulating box to base portion to minimize heat loss by conduction through base and sides of the fin array. Calibrated thermocouples (k-Type) with temperature indicator are used to measure temperatures at various locations of fin array. A calibrated wattmeter is connected to measure heater input. Experiments are performed and steady state observations are recorded.

ANSYS Fluent 12 software is used for Computational fluid dynamic analysis. The fin surfaces, with base are assumed as a source, held at uniform temperature. Laminar natural convection is the mechanism for heat transfer from the fin array. Radiation heat loss is not considered. The Boussinesq approximation is employed. ANSYS-workbench is used to create geometry of model. Geometry and meshing capabilities within ANSYS Workbench is done. The 3D geometric model of inverted notch fin array is created. Figure 2.19 shows the 3D geometry model which is created in ANSYS fluent consisting the fin array assembly and enclosure for natural convection condition. After creating the geometry, the next step is to prepare the mesh, accuracy of the CFD analysis depends on the quality of mesh. Mesh generation involves the application of elements and nodes on existing geometry.  The unstructured mesh is used to mesh the solid model. The tetrahedral element is used for meshing the model. Figure no 2.20 shows the meshed model in ANSYS Fluent software.

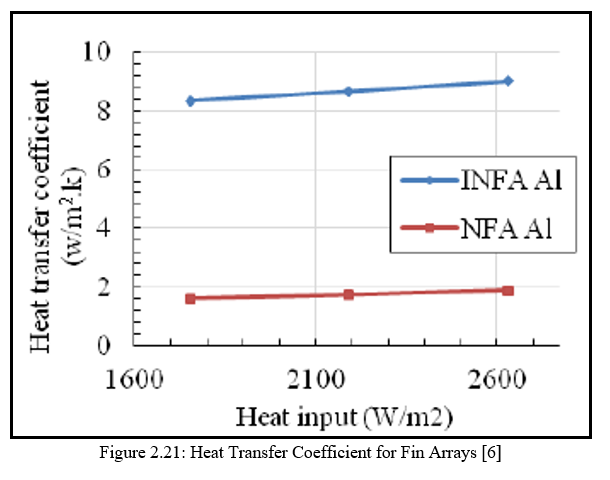
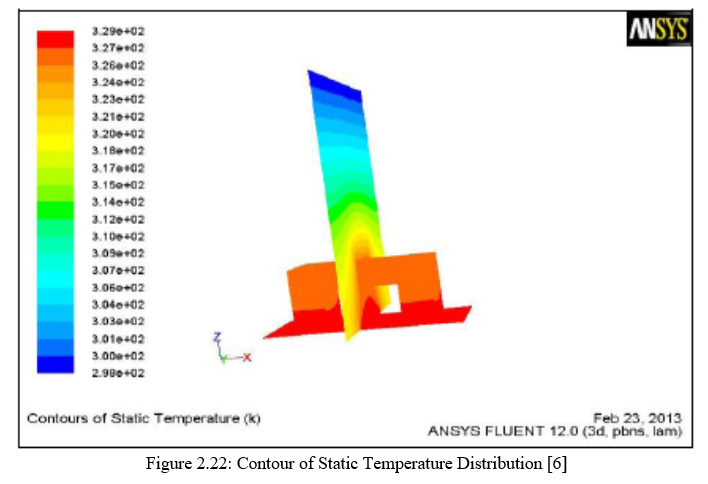
Figure 2.21 shows that effect of heat input on heat transfer coefficient for inverted notch fin array and normal fin array. The value of Lc for without notch fins is 0.0585 m and for notch fins the value of Lc 0.03234 m. The heat transfer coefficient is value of h is depends upon the ratio Nu/Lc. The heat transfer coefficient is directly proportional to Nusselt number. The value of Nu is affected as Lc is increase or decrease. In notch fins the value of Lc is less than without notch fins. Hence the value of h is more in notch fins than without notch fins. It is observed that more temperature difference in notch fins hence ultimately increase the value of heat transfer coefficient. The temperature distribution over the entire body is calculated by the CFD analysis. The contour of static temperature distribution is shown in figure 2.22.

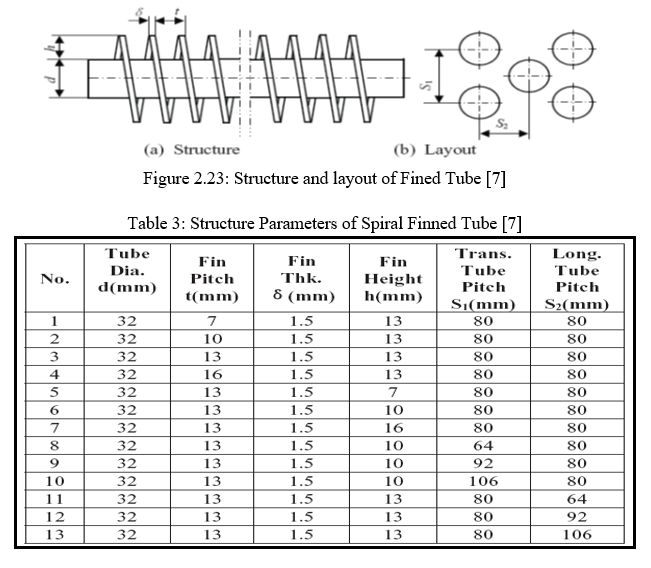
He FaJiang et al. [7] has explained about the physical setup and analysis done on the on various fin structures. The author and the team have performed the complete analysis on design of experiments (DOE). Figure 2.23 explains model for which the design of experiments are performed. He has done 13 parameters with 2 layers. Table 3 show the same.

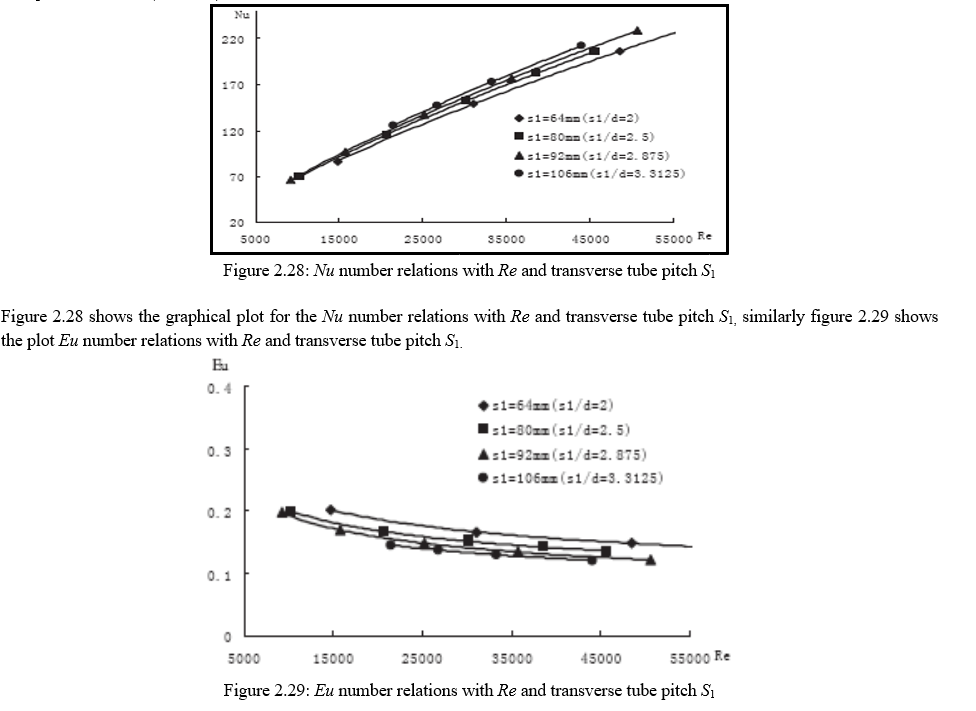
Experimental analysis shows the relationship between the Nusselt Number (Nu) and flowing resistance (Eu) with the Reynolds Number (Re). Figure 2.24 the graphical representation of Nusselt number (Nu) with the Reynolds number (Re), Similarly figure 2.25 shows the representation of Eu with the Reynolds number (Re).

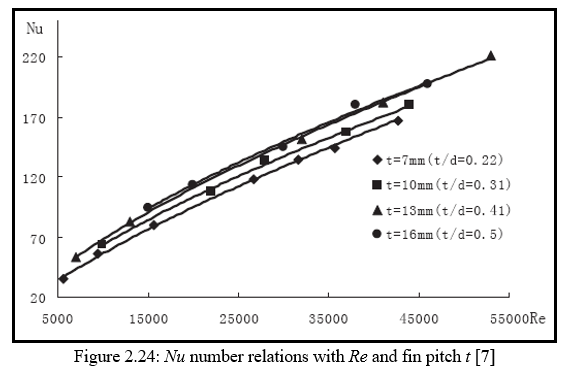
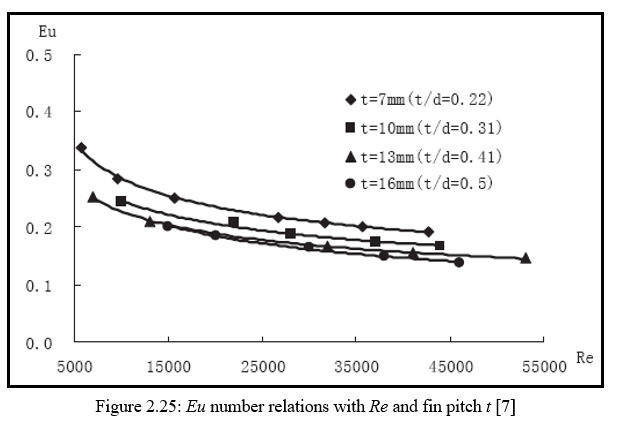
Following are the parameters that are used for performing Heat transfer Nu number and flowing resistance Eu number relations with Re number (Re=5×103~5.5×104) and fin pitch t under constant tube diameter (d=32mm), fin thickness (δ=1.5mm), fin height (h=13mm), transverse tube pitch S1=80mm(S1/d=2.5), longitudinal tube pitch S2=80mm(S2/d=2.5)

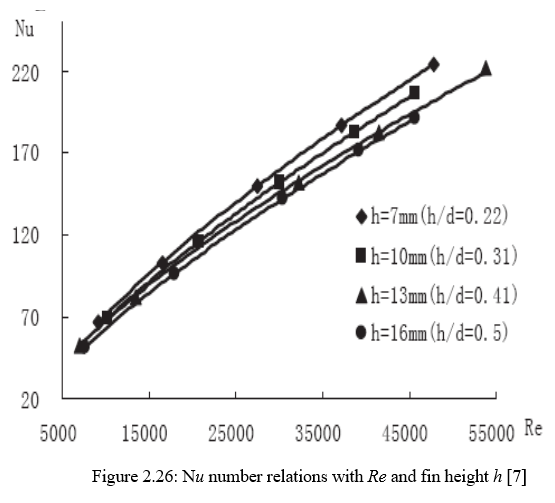
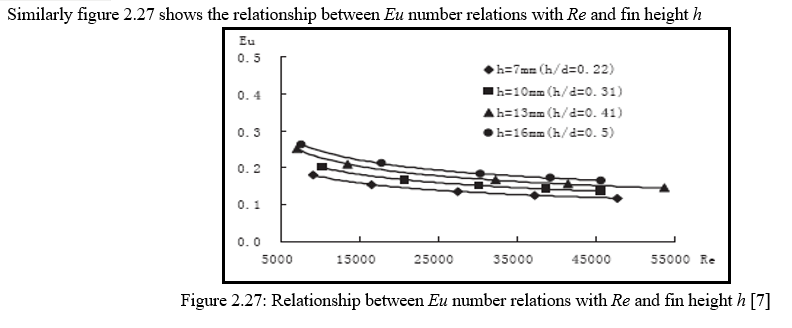
Further the author still to find the relationship of heat transfer and the flowing resistance with the fin height. The parameters that are use are as follows Heat transfer Nu number and flowing resistance Eu number relations with Re number (Re=5×103~5.5×104) and fin pitch t under constant tube diameter (d=32mm), fin thickness (δ =1.5mm),fin height (h=13mm), transverse tube pitch S1=80mm(S1/d=2.5), longitudinal tube pitch S2=80mm(S2/d=2.5). Figure 2.26 shows the Nu number relations with Re and fin height h

Further the author speaks about the effect of transfer pitch on the heat transfer and the flowing resistance. The parameter which were used were as follows

Heat transfer Nu number and flowing resistance Eu number relations withRe number (Re=5×103~5.5×104) and transverse tube pitch S1 under constant tube diameter (d=32mm), fin thickness (δ =1.5mm), fin pitch (t=13mm), pitch height (h=10mm), longitudinal tube pitch S2=80mm (S2/d=2.5)

Esmail M.A. Mokheimer [8] has investigated the performance of annular fins of different profiles which are subjected to locally variable heat transfer coefficients. The working performance is measured in terms of the efficiency of the fin, which is further a function of the ambient temperature and the geometry of the fin. The overall performance is obtained is measured from the curves which are plotted called as the “fin efficiency curves” the author further reveals about the calculations and the performance is based upon the constant heat transfer coefficient. If the natural heat transfer coefficients dominates the constant heat transfer coefficient at that times local heat transfer coefficient are been used for such cases. The aim in using the local heat transfer coefficient is that it is the function of the local temperature. The results that have obtained are for various annular profiles having cross section such as rectangular, triangular, concave parabolic and convex parabolic

Following are some of the assumptions made while the author is carrying the study:

1. Steady heat flow.
2. The fin material is homogeneous and isotropic.
3. There are no heat sources in the fin itself.
4. The heat flow to or from the fin surface at any point is directly proportional to the temperature difference between the surface at that point and the surrounding fluid.
5. The thermal conductivity of the fin is constant.
6. The heat transfer coefficient is the same over the entire fin surface.
7. The temperature of the surrounding fluid is constant.
8. The temperature of the base of the fin is uniform.
9. The fin thickness is so small compared to its length and width that temperature gradient normal to the surface may be neglected.
10. The heat transferred through the outermost edge of the fin is negligible compared to that passing through the sides.

The author has done study on the local heat transfer coefficient along the upper and the lower surface of the fin. The fin performance is represented by the fin efficiency. Figure 2.30 depicts the annular fin profile and shows the important main geometric profile parameters. The fin profiles are defined by the change in the thickness of the fin along the length of the fin. The general equation is given by:

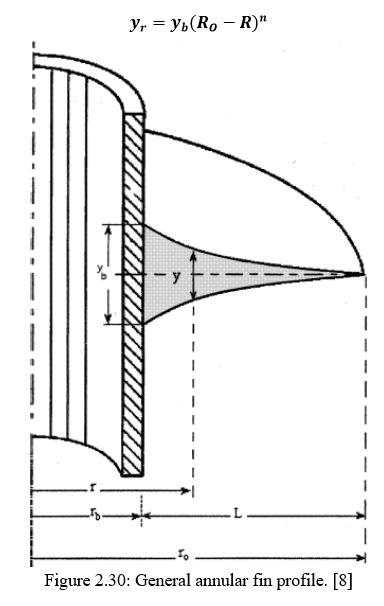
In all of the above equations there are 2 dimensionless controlling parameters in addition to the index n. The 2 parameters are namely the dimensionless variable m and the fin radius ratio.

The results that were obtained for annular fin subjected to variable heat transfer coefficient are shown in figure 2.31-2.35 for rectangular, constant flow area, triangular, concave and convex profile respectively. Figures 2.31 and 2.32 shows the available analytical solution plotted by dotted lines which is the actual deviation between the constant heat transfer coefficient and the variable heat transfer coefficient.

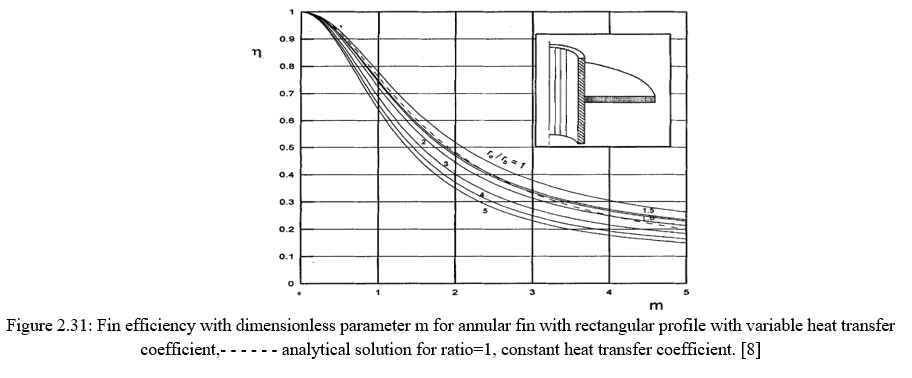
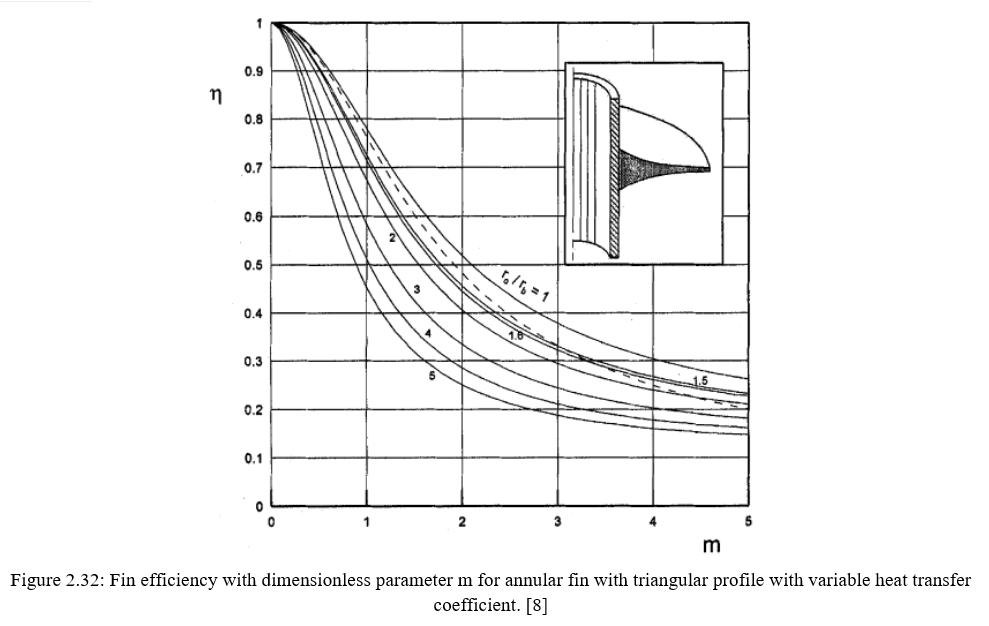
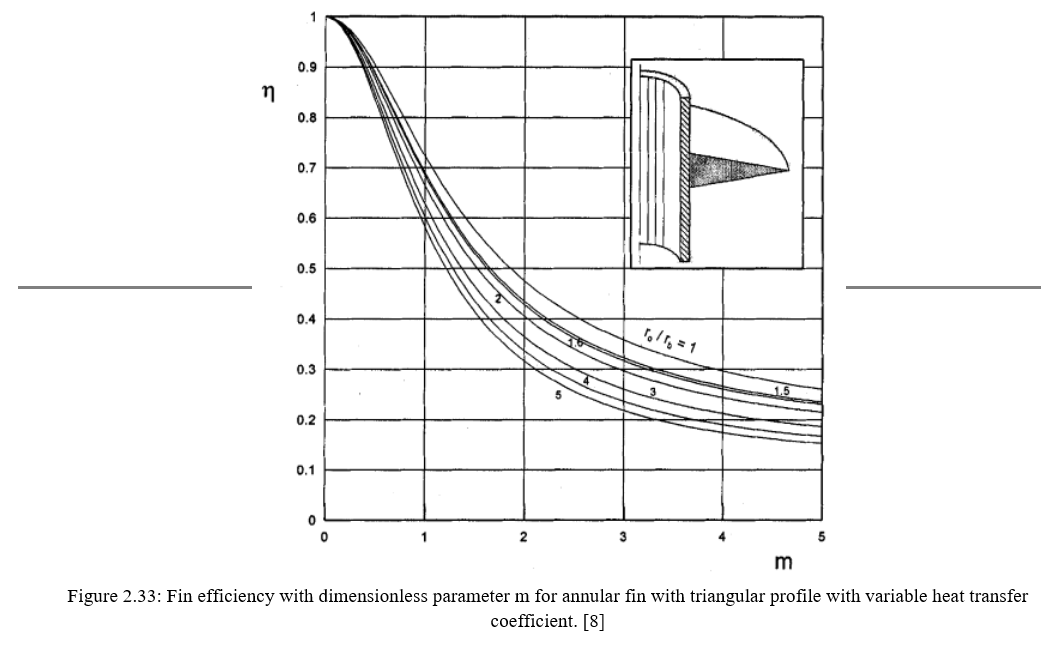
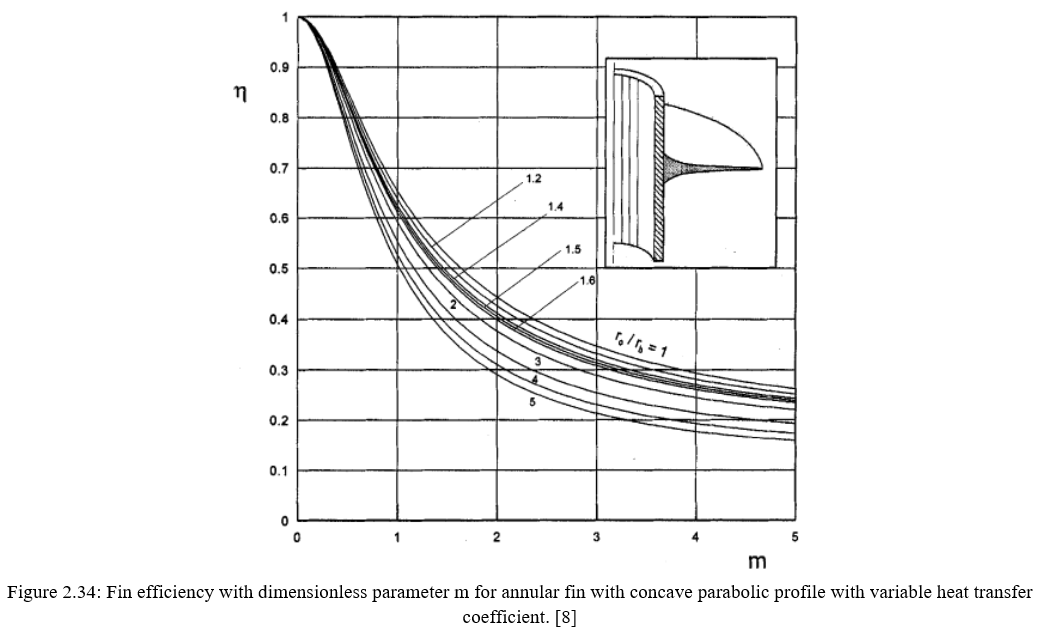
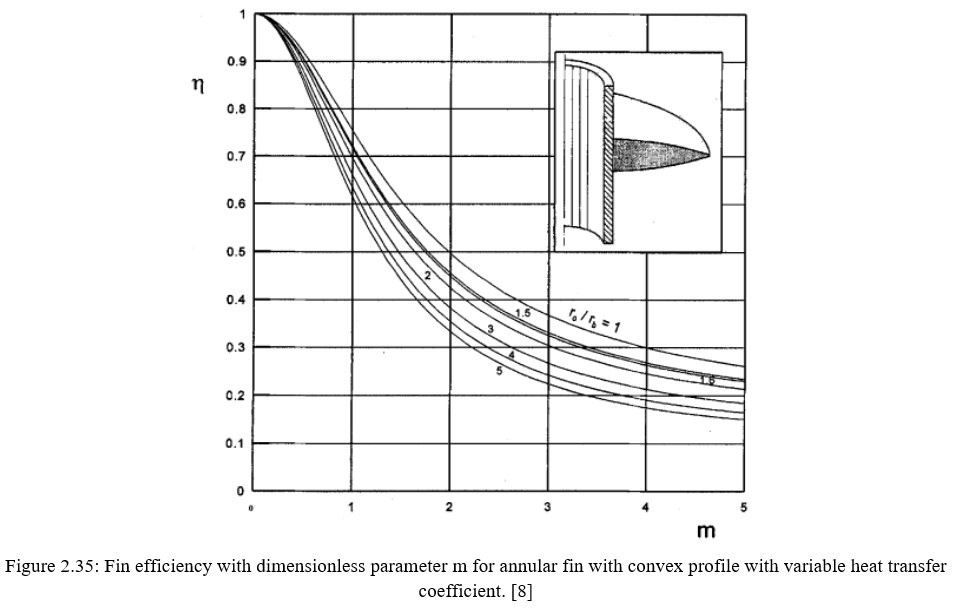
Finally to conclude the author says the deviation between the fin efficiency calculated based on constant heat transfer coefficient and that calculated based on variable heat transfer coefficient increases with both the dimensionless parameter m and the radius ratio of the fin. The use of the present results obtained for  heat transfer equipment that involve annular fins subject to natural convection heat transfer mode would result in a considerable reduction in the extended surface area and hence a significant reduction in the weight and size of the heat transfer equipment.

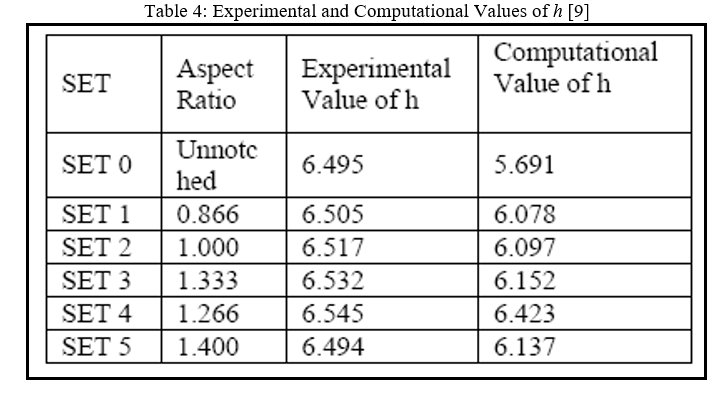
S. H. Barhatte, M. R. Chopade [9] has experimentally proved that increasing the area of heat transfer will definitely help in increase the heat transfer rate. The author reveal about the ideal of developing a triangular not at the base of the fin base. The idea behind doing is to increase the overall heat dissipating area. The notch shown in figure 2.36 is been made on the solid model and tested in ANSYS for the heat transfer analysis. Now further the author says about the shape of the triangle that has to be constructed is also important. The ratio of height of the triangle to the base of the triangle called as the aspect ratio is also of importance.

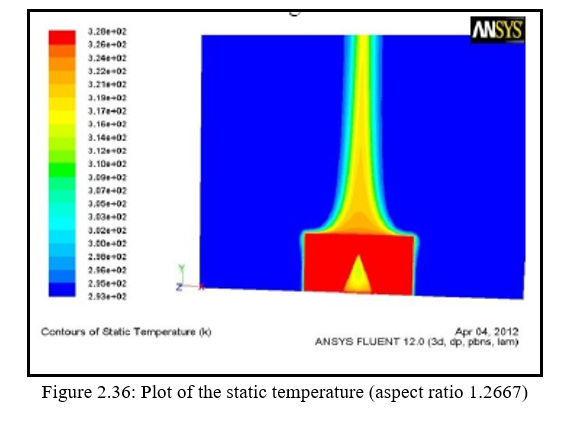
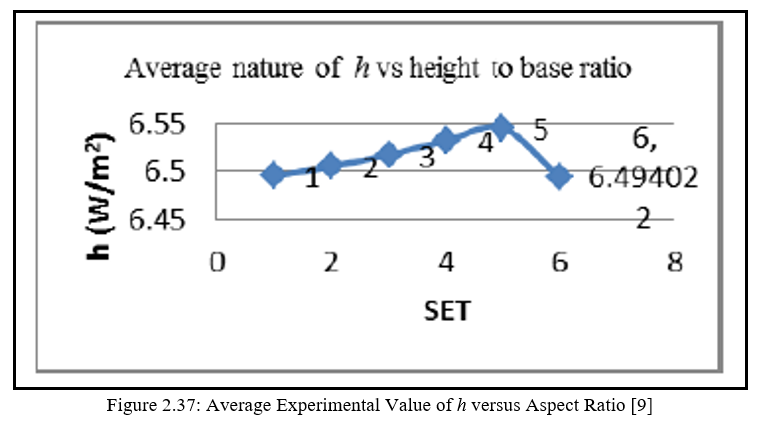
Further the he has performed some test by changing the aspect ratios. Table 4 gives the details for the same, it also explains about the value of heat transfer “h” for both the experimental and the computational method. The triangular notch having the aspect ratio of 1.266 has the maximum value of the heat transfer, for aspect ratio 1.266 the corresponding value of h is 6.545 experimental and 6.423 computationally. These both value of heat transfer is having the maximum value among the group. The same is been showed in graph shown in figure 2.37.

Sikindar Baba.Md et al. [10] has explained some techniques that help in the increasing the heat transfer rate by increasing the surface area. The amount of the surface area determines the amount of conduction, convection and radiation that is transmitted through the body. Increasing the temperature difference the object (fin) and the environment increase the convection heat transfer coefficient.

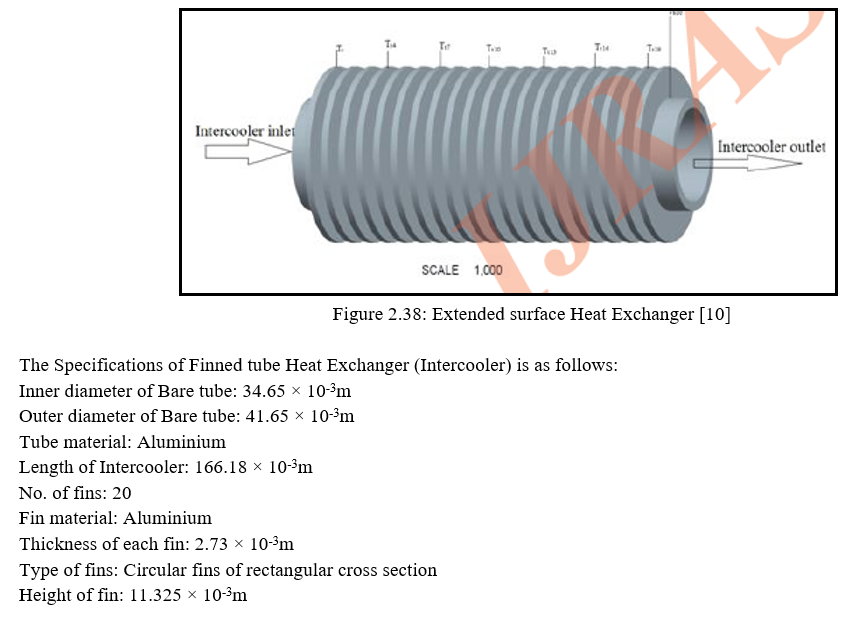
The author has performed some test on the finned tube heat exchanger. Inter cooler of two stage reciprocating air compressor is considered.  It has 20 fins on the body. These fins are also called as the annular fins which have rectangular cross section. Figure 2.38 shows the construction features of the same.

The author has performed some experimental test and found out some results based on test performed. Table 5 explains about the temperature difference between the base of the fin and the tip of the fin. Further he has computed the temperature which lies between the outer

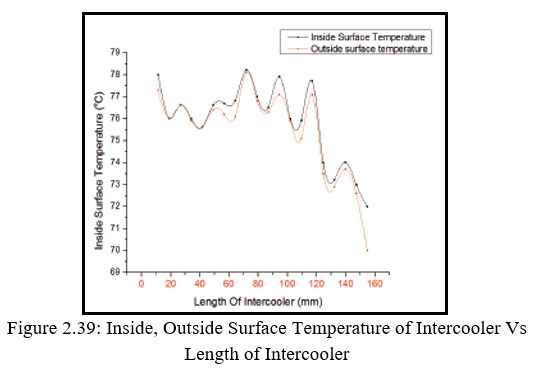
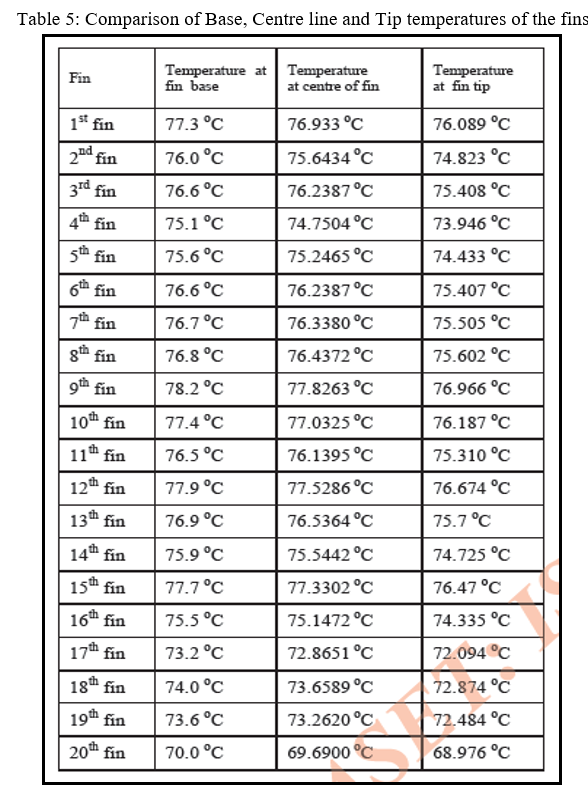
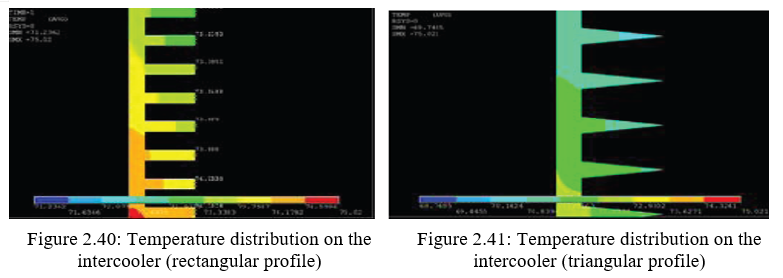
Surface and  inner surface  and which is measured along the  length of the inter cooler. The temperature difference between those two surfaces is very litter since the thickness is 3mm and the thermal conductivity is very high. Figure 2.40 shows the temperature distribution of the rectangular fin, similarly figure 2.41 shows the temperature distribution for triangular fin. The analysis shows that in the case of triangular shape fins the heat transfer id more and optimized one since the area of heat transfer is increased and material cost is also reduced. If actual results are plotted heat transfer rate is increased by 3.39%. 

III. INNOVATIVE AND OPTIMIZED DESIGN STRATEGIES FOR FIN BODY

A. Introduction

There are many ways by which the heat transfer can be enhanced in the fin body. The various method by which the heat transfer depend upon the various constructional features such as thickness of the body, the cross section of the body, the number of the fins, the distance between the adjacent fin, the length of  the fin from the base of the fin. All of the above parameters individually or in combination are somehow related in increasing the cross sectional area from which the heat dissipates.

All of the above parameters are equally responsible for deciding the heat transfer rate through the fin body. Analyses of various parameters are being done through on a base model which has different cross sections such as rectangular, trapezoidal, parabolic, and concave. Similarly other combination such as the aspect ratios of the cut-out of profiles made in the fins also plays a vital role in defining the performance of the fin. All of the above parameters are consider while executing the project.

B. Component Under Study: Fin body of the Compressor Head 

Figure 3.1 shows the actual fins that are present on the compressor head. These fins that are provided may just be made from the point of view for heat dissipation. The heat which is generated in the system (compressor) may not be dissipated in an ideal way where the heat transfer rate would be maximum; an attempt is made to study on the above component and try to modify the design parameter for optimizing the heat transfer rate.

. C. Component Nomenclatures of single cylinder air compressor

       

D. Work Methodology for Project

E. Dimensional Parameters of the Existing Design

 

a: pitch, distance between two adjacent fin

b: thickness of the fin at the tip

c: external diameter of the of the central body

d: internal bore diameter of the central body

e: total height of the fin body

f: square base of the fin body

g: distance between the base and the last fin in vertical direction

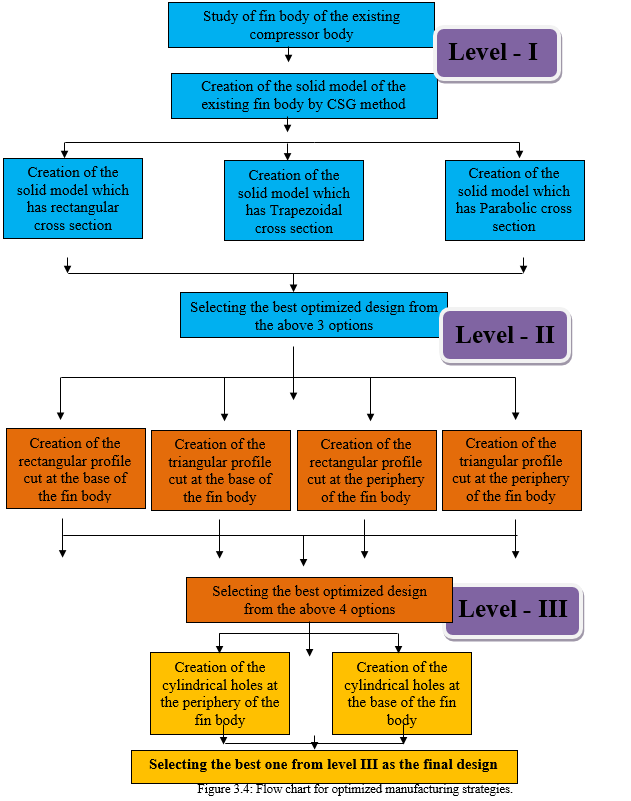
F. Level I Design – Basic cross section

1. Design of Square fin Body: The straight fin is one of the base cross section that analysed during study of heat transfer from a body. The general idea is having a constant diameter ‘d’ projecting uniform cross section are the length of the fin i.e. the length of the fin tip measured to the base of the bore diameter is kept depending upon the physical aspects of manufacturing as well as the available space constraints. Similarly the pitch that is maintained between two adjacent fins is also of utter most importance. This pitch value decides the volume of air that will come in contact with the fin and which is basically responsible for developing the temperature gradient, ?t

The factors that are affecting heat transfer as follows:-

a. Increasing the temperature gradient (?t) between source temperature and the fin tip temperature.

b. Increasing the heat transfer coefficient.

c. Increase the surface area of the body.

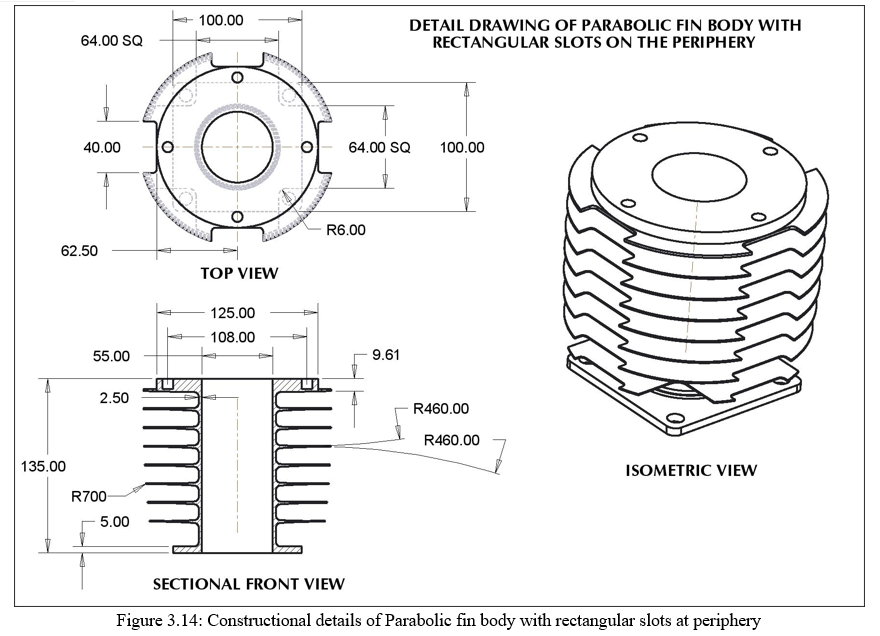
In our design we have kept the diameter of the bore as 55mm, which cannot be changed as constraint dimensions of the component. The maximum diameter of the fin becomes around 130mm +/- 5mm. The length of the fin become an (130-55)/2 = 75/2 = 37.5 mm approximately. The outer periphery of the body is having a radius of R700 maintained between toppest and lowest height of the fin. The thickness of the tip is 2.5mm. The complete body stand on a 64 mm square base. The construction features are showed in figure 3.6. & 3.7

 

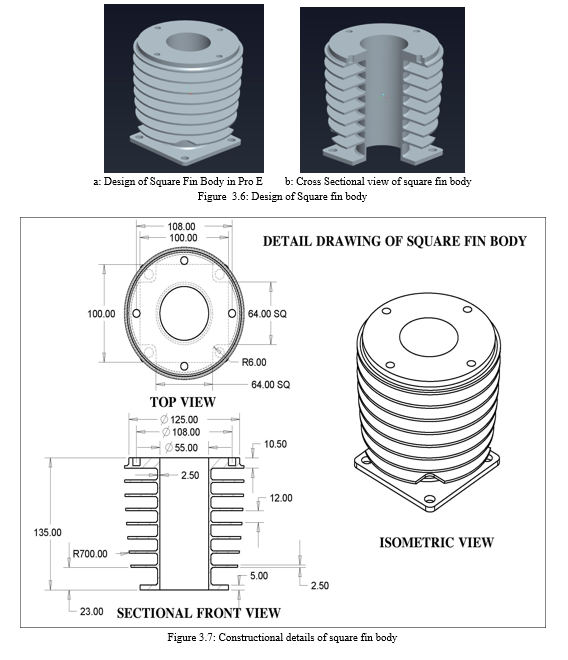
2. Design of Trapezoidal fin Body: The trapezoidal fin is another important crossection that is to be discussed. Already discussed in section 3.5.1, that the length of the fin is 37.5mm, the thickness is around 2.5mm. The heat transfer can be increased by increasing the physical surface area. The surface area can be increased by just giving a draft starting from the tip of the fin. There will be physically increase in the length of the fin that will be exposed to the air. Initial the length of fin i.e. 37.5mm will be having a new length which is greater than 37.5mm. The length will be depending on the degree of draft provided which starts at the tip of the fin. The final result of adding draft to the fin body gives additional strength and rigidity to fins. Since the thickness is greater than 2.5mm. This case is physically applicable for increasing the heat transfer. The material that is for used manufacturing also play an important role. The total weight of the fin body should also be less at a competitive price. Both of the above two points can be achieved by just reducing the thickness of the fin below 2.5mm. This reduction in thickness will have no effects in the increased heat transfer area as well as the weight of the component will be reduced. The final thickness that’s maintained is 0.9mm. The constructional features are shown in fig 3.8 and 3.9

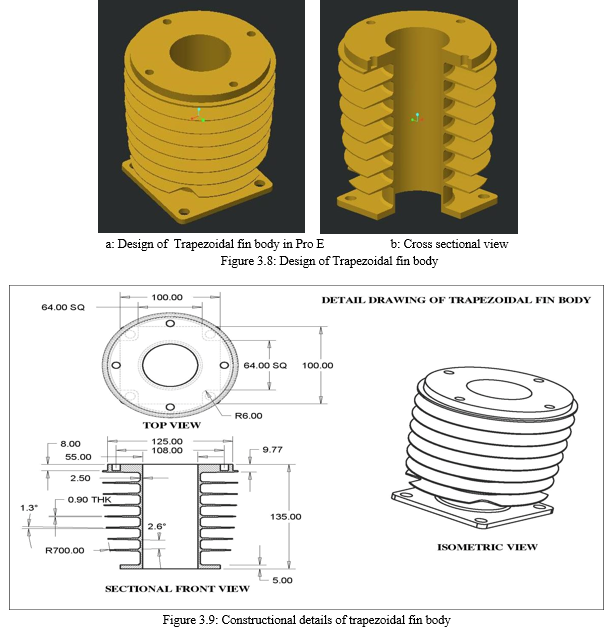
3. Design of Parabolic fin Body: As earlier discussed, that the heat transfer mainly depends upon factors such as, the surface area, heat transfer coefficient, and the temperature gradient (?t). The temperature gradient (?t) and the heat transfer coefficient cannot be altered. In this case the only parameter that can be altered is the physical area of the component. Further enhancement can be done by the change in the surface area. This can be done in terms of changing the cross section from trapezoidal to parabolic in nature. The area is changed from linear to parabolic in nature. This is physically done by replacing the straight line between the bore diameter and the tip of the fin by a curve of parabolic nature.   The surface projected by the parabolic surface will be definitely more than that of the trapezoidal fin body. The parabolic area is created by plotting R460 between the tips and the base of the fin. The constructional features of the fin is showed in figure 3.11

G. Level II Design – Profile pocket on fin area

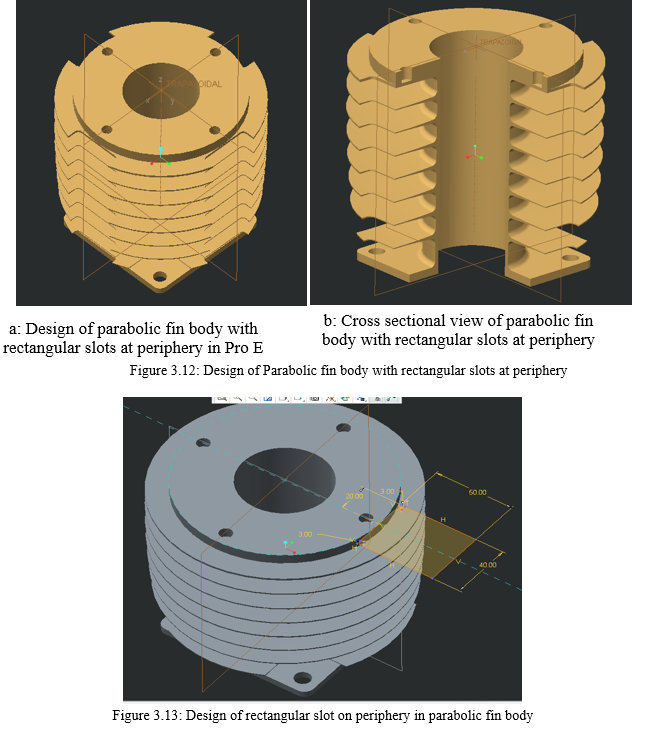
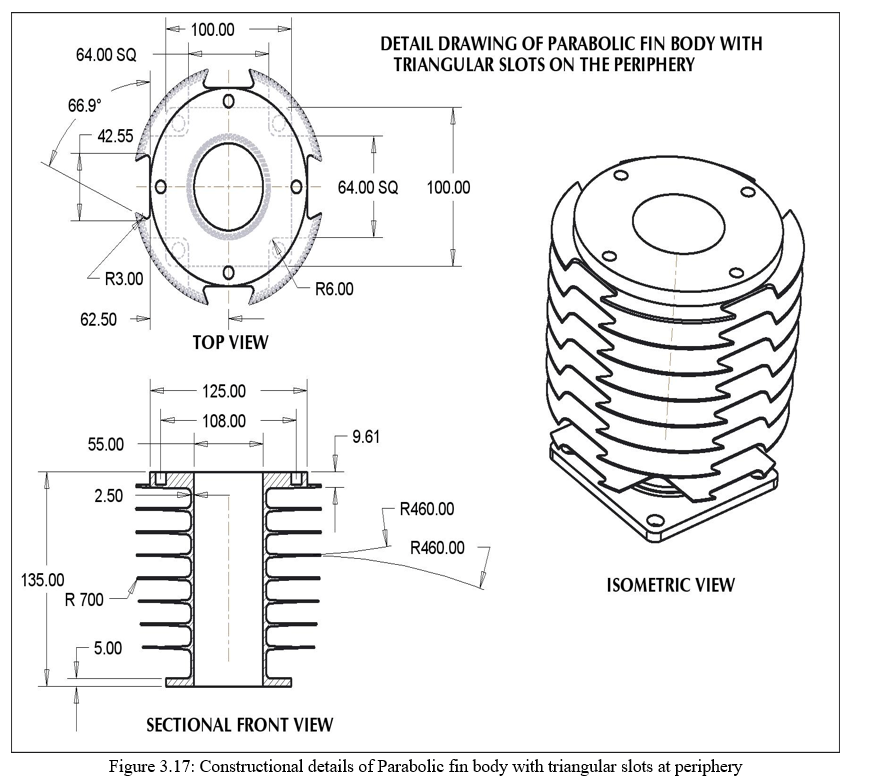
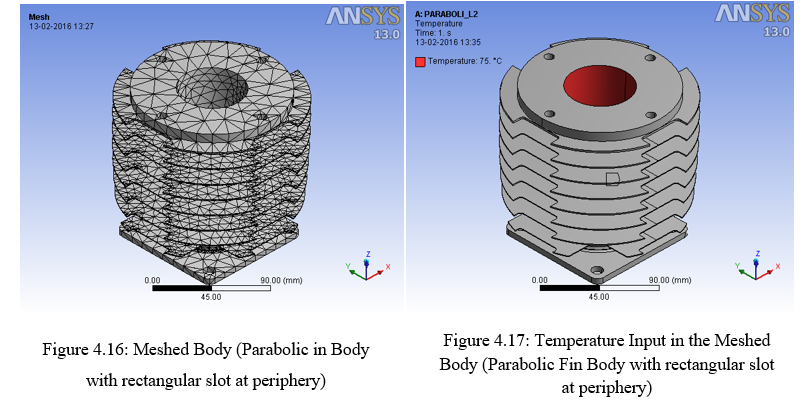
1. Design of Parabolic fin Body with Rectangular Slots At periphery: As earlier discussed the only parameter that can be altered is the physical surface area of the fin body. In level I design we have only made the alterations in the thickness of the fin and the cross section. In level II design an attempt is made to increase the physical surface area at the cost increase in the fin length. The length of the fin is increased in some fixed % which is feasible for manufacturing as well as suit the physical assembly of the existing setup. In our existing design the fin is further extended by 8mm, meaning that there is increase in 21.6% area of the existing area. There rectangular cut made ath he tip of the fin. The dimensions of the rectangular end are about 13.5 x 40 mm wide. 4 slot are made at 90° with adjacent one. This size of cut is just made on the random basis just to check if there is any drop in temperature. Definitely since there is increase in the area, connecting the Level I design; higher temperature gradient will lie across the fin cross section area. The details of the rectangular cut are showed in fig 3.12 and 3.13 respectively. There are six rectangular pockets which are inscribed in 30° between R 41 and R 33.16

          

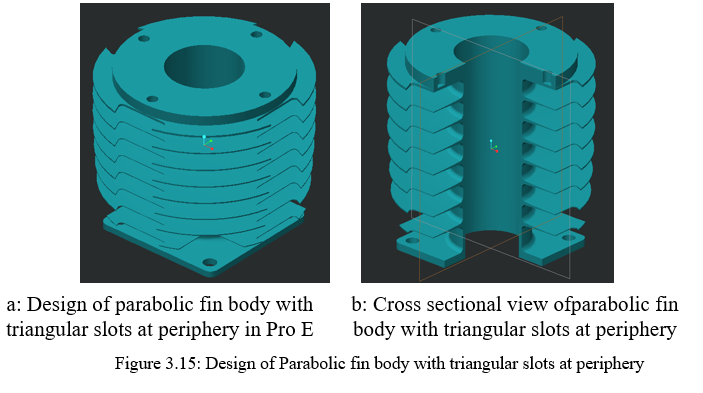
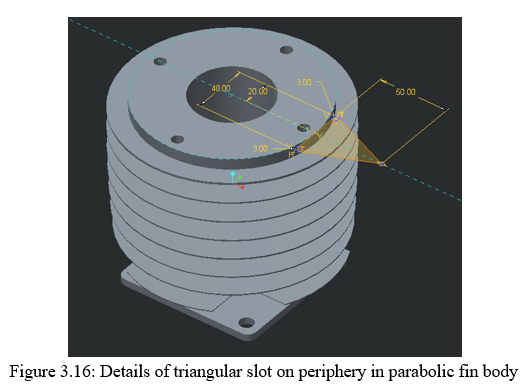
2. Design of Parabolic fin body with Triangular Slots at Periphery: Increase in the surface area can further be explored by altering the different cross section. As we have checked for rectangular cross section area; an implementation is done on the triangular area. Plotting of triangular area against rectangular one will allow more material that will be placed on the fin. The only change done is the triangular profile cut v/s rectangular cut is as follows, the triangular profiles is having a base of 40mm to height of 50mm. The triangular area is removed same in the case of rectangle one. The details of the same are showed in figure 3.15 and 3.16 respectively.

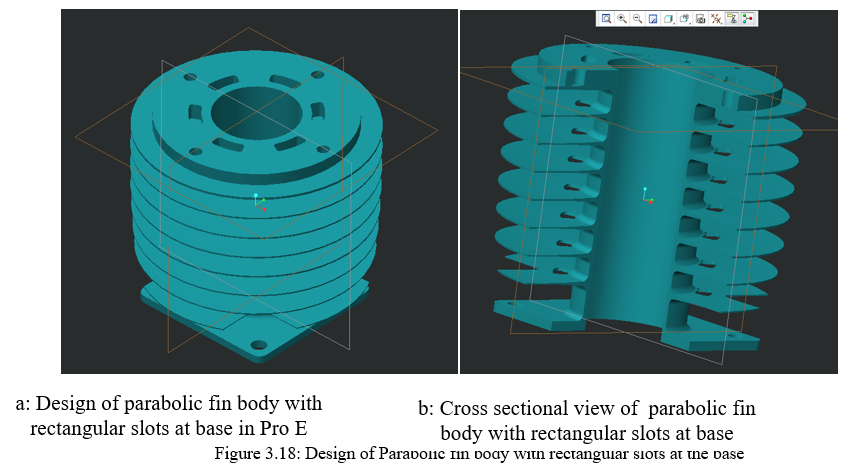
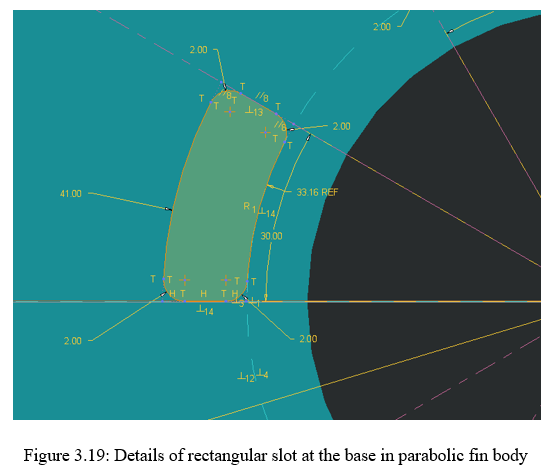
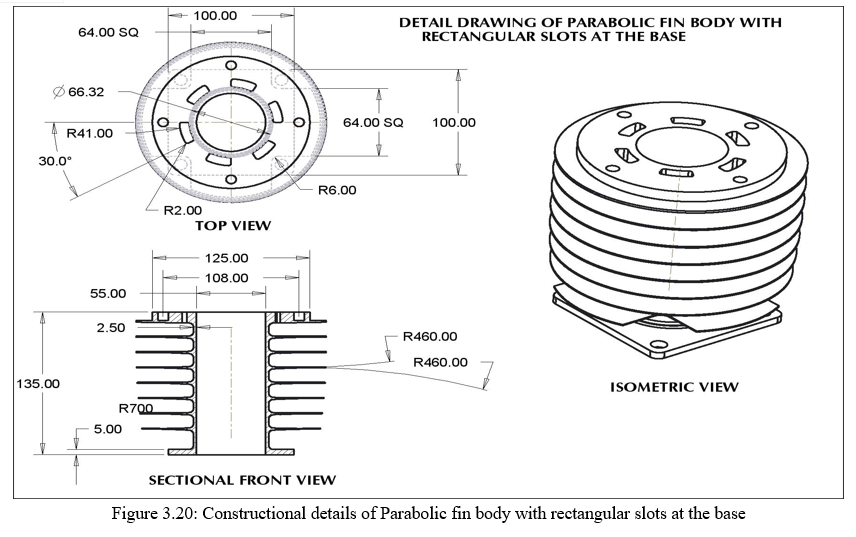
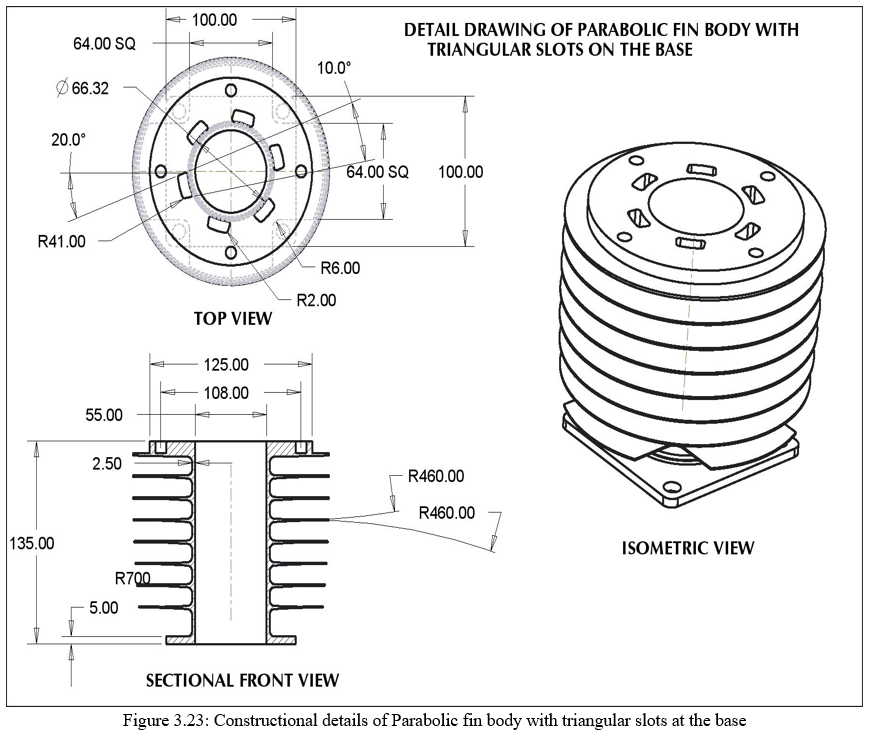
3. Design of Parabolic fin body with Rectangular Slots at the Base: The last two alterations are done on the periphery of the fin body. Alteration at the base of the fin body is also prime importance. A rectangular slot is removed just at the start of the fin length. A rectangular pocket of R41.00mm and R33.10mm as the adjacent sides of the rectangular pockets with the other two ends of the slots are inscribed in 30°. There are in all 6 pockets which are cuts at the base. The size of the rectangular pockets plays an important role because the remaining area that is present on the body should be capable of handling maximum heat transfer at the same time. Similarly it should be able to resist against the physical damage. Considering equal weight age to area 50% of the areas inscribed in the radii is removed in the slot area and 50% is kept on the fin body. The details are of the construction features are shown in figure 3.18 and 3.19 respectively.

4. Design of Parabolic fin body with Triangular slots at the Base: As discussed earlier from 3.5 onwards there should be ample amount of area that should be present on the base of the fin. The adjacent edges that are inscribed in 30° are set back at 20° each which will leave more material on the fin body near the fin base. This will allow maximum heat transfer via maximum area obtain by setting the adjacent edges at 20° each. However, it won’t be commentable by adding more area near the base would increase the heat transfer since it is very close to the source temperature. The physical answers that are obtained in the software’s will guide the importance of adding additional area at the base of the fin. Figure 3.21 and 3.22 explains the constructional for the same.

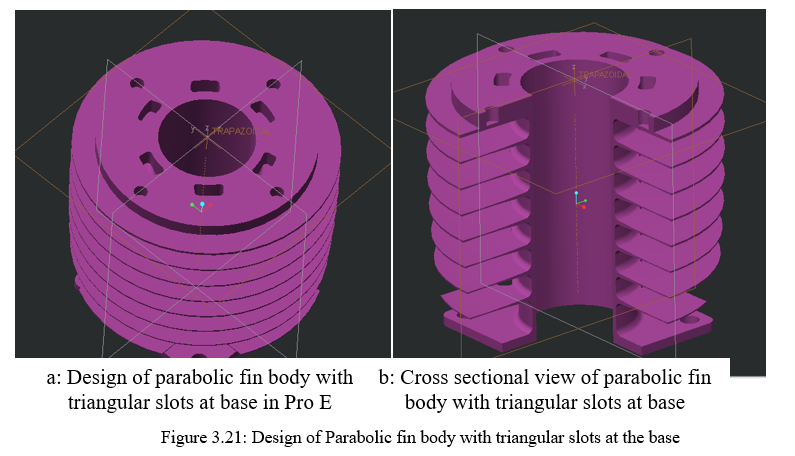
H. Level III Design- Cylindrical slot on fin area

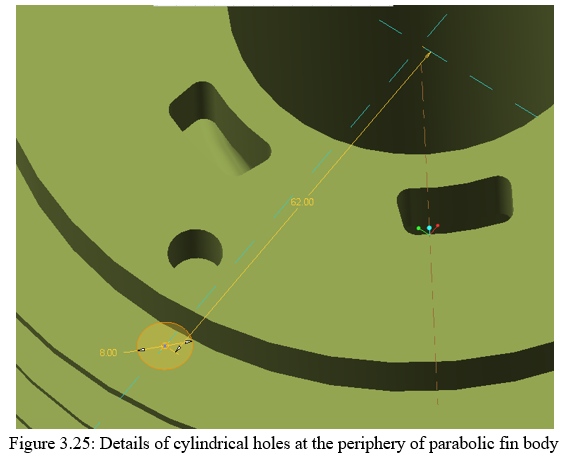
1. Design Of Parabolic Fin Body With Rectangular Slots At Base With Combinations Of Cylindrical Slot At The Periphery Of The Fin Body: The combination of the square pocket or the triangular pocket that is made at the base of the fin is made on the assumption of 50% of area is cut off from the fin area and the remaining is left on the fin for providing maximum heat transfer conditions. There is no scope for creating any additional pocket near the base of the fins because it decreases the strength of the fin.  Further heat transfer can be improved by creating cylindrical slots in between the slots which are created at the base of the fin. Creation of slots will definitely provide more surface are for heat dissipation. Figure 3.24 - 3.26 shows the same.

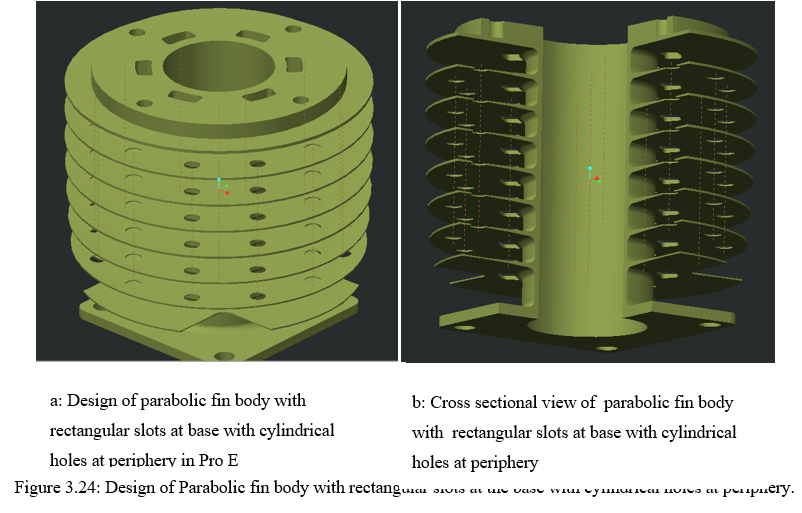
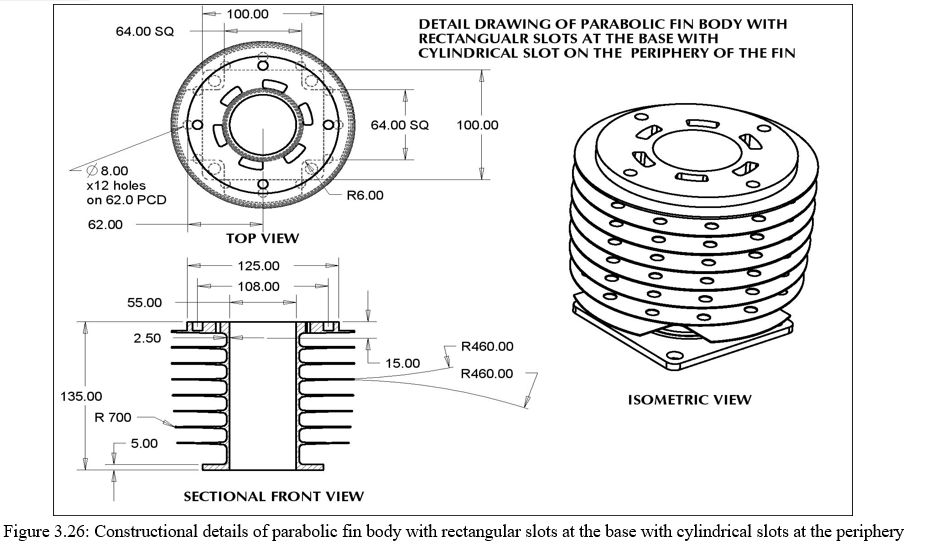
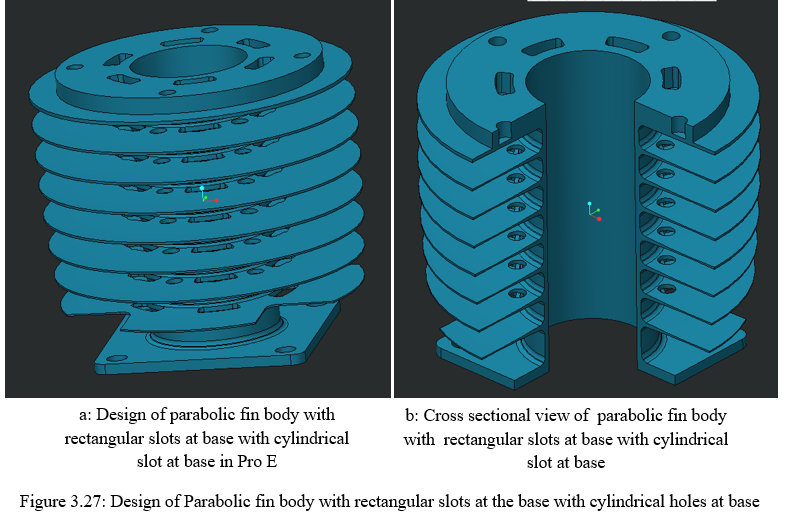
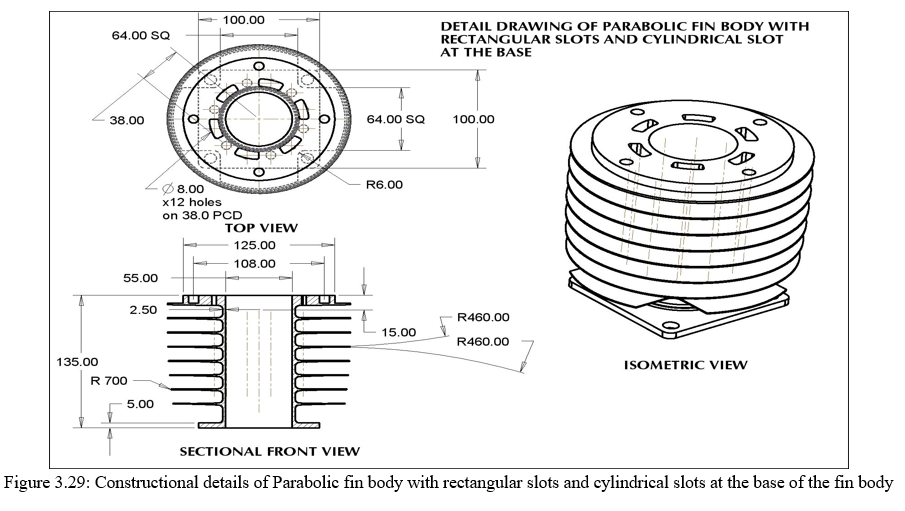
2. Design Of Parabolic Fin Body With Rectangular Slots At Base With Combinations Of Cylindrical Slot At The Base Of The Fin Body: The change in design for this segment as compared to section 3.8.1 is that the holes that are made on the periphery are now shifted to the base of the fins. The size of the hole plays an important role as it is responsible for maximum heat transfer as well as provides high strength. The detail for the same is shown in figure 3.27 -3.29.

IV. CAE ANALYSIS OF VARIOUS CROSS SECTIONS IN ANSYS

A. Introduction

Ansys mechanical software is used plotting the results. The software is finite analysis tool used for structural, static and dynamic, linear and non linear, thermal CFD and etc. In the complete design set Ansys work bench is used as the basic software for analysing the thermal analysis of the compressor fin body. The input to the Ansys software was provided from Pro Engineer software. The IGES format was provided to the software rest all boundary condition and thermal load were applied which plotted temperature distribution total heat flux. The various distributions are explained in section 4.2 in detail.

B. Level I Design: Different cross section of the fin body

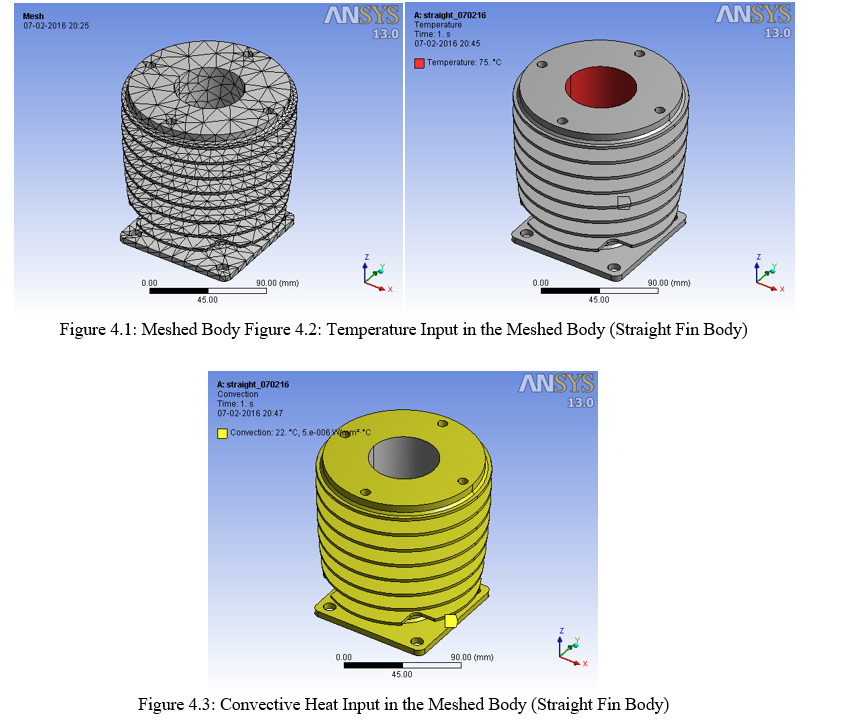
1. Straight Fin Body

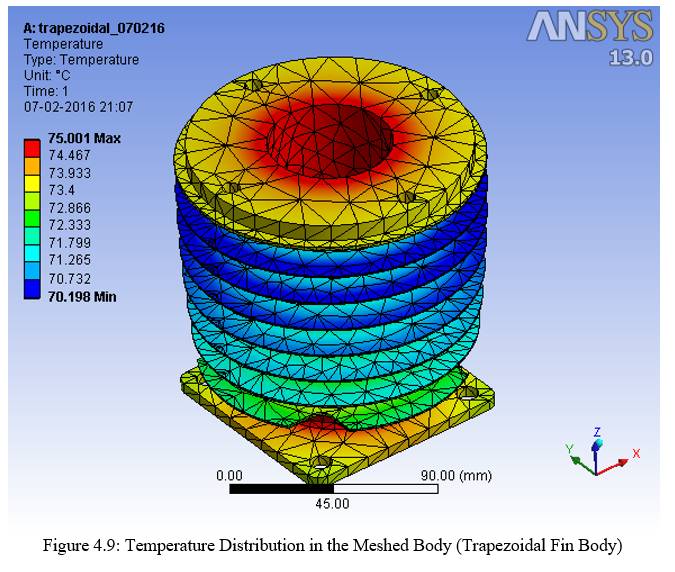
2. Trapezoidal Fin Body

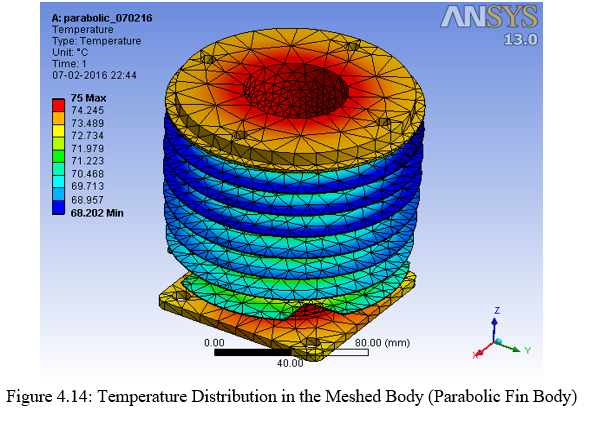
3. Parabolic Fin Body

C. Level II Design: Creation of cut on the Periphery of the Fin

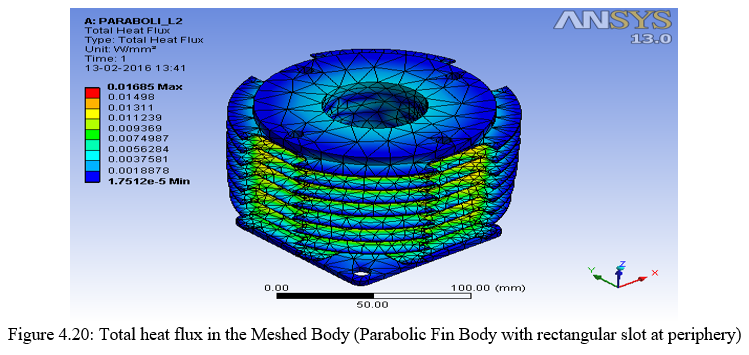
1. Parabolic fin body with rectangular slot on the outer periphery of the fins

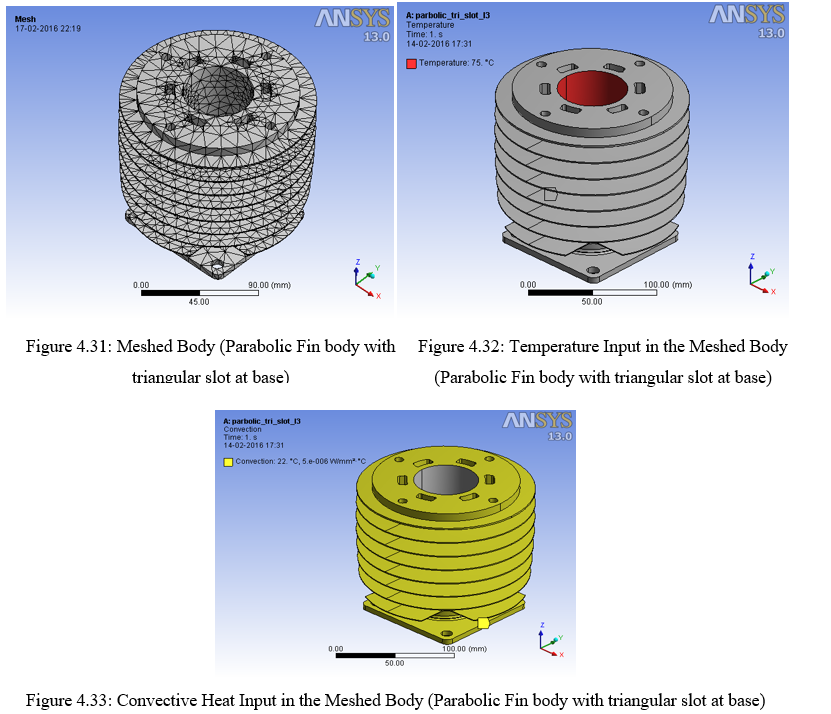
2. Parabolic fin body with triangular slot on the outer periphery of the fins

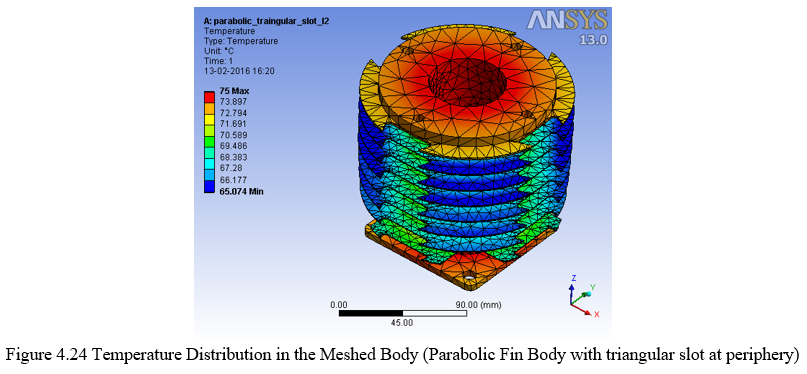
3. Parabolic fin body with rectangular slot at the base of the fins

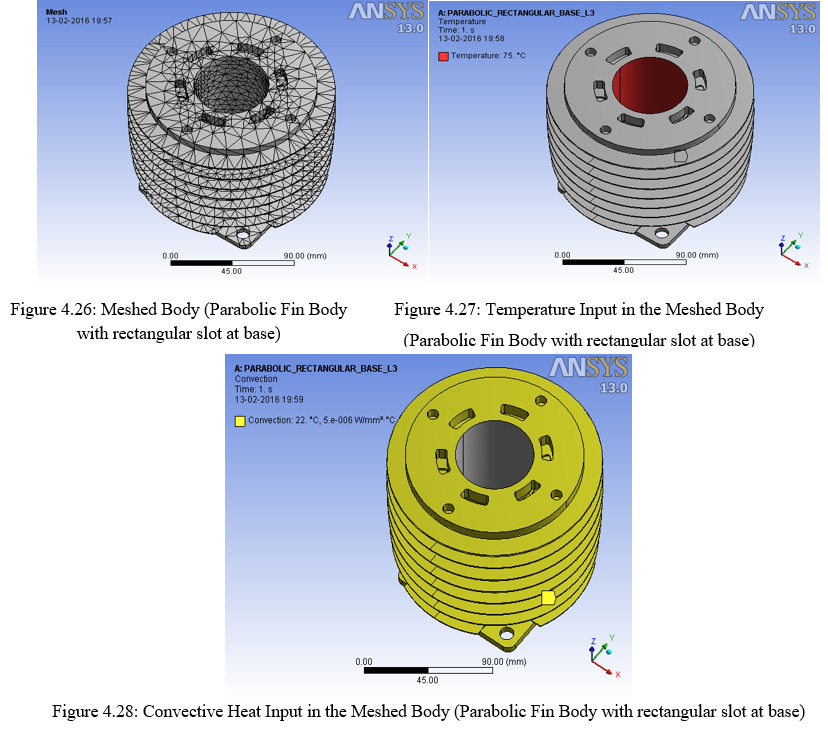
4. Parabolic Fin Body With Triangular Slot At The Base Of The Fins

D. Level III Design: Creation of cylindrical slot

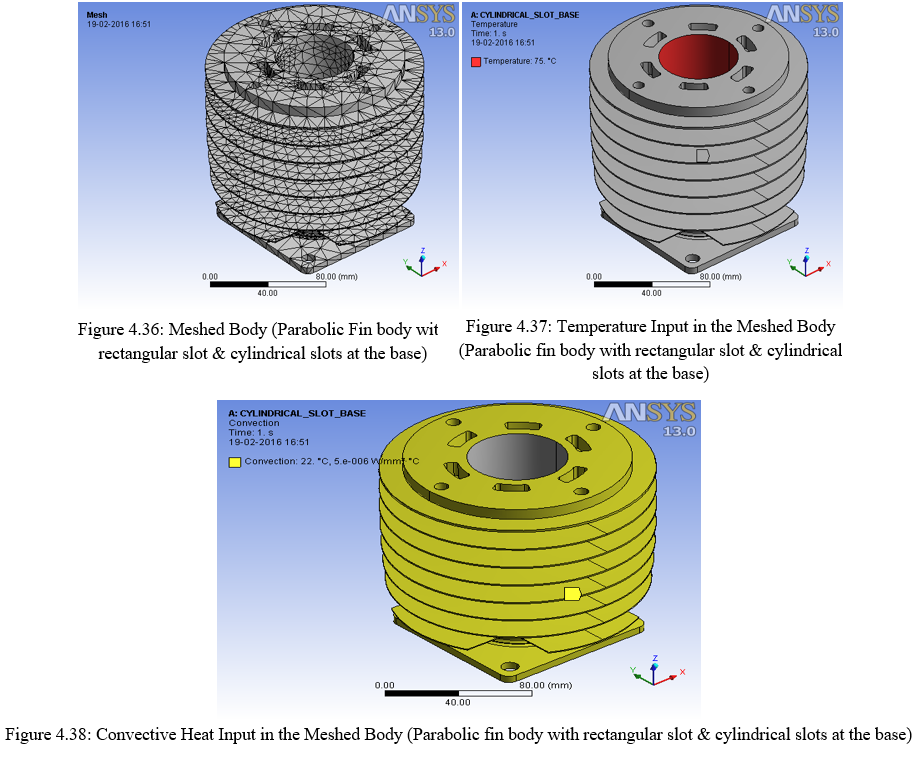
1. Parabolic fin body with rectangular slots at base with combinations of cylindrical slots at the base of the fin body

2. Parabolic Fin Body With Rectangular Slots At Base With Combinations Of Cylindrical Holes At The Periphery Of The Fin Body

V. RESULTS AND DISCUSSION

A.  Results.      

Analysis of various different fin bodies having different cross section is done. The result is carried out in Ansys 13 Work bench. The results that are carried out are under normal working conditions. Mainly more focus is put on the temperature gradient (?t),  that is present between the source temperature and the fin tip temperature. More the temperature gradient obtained, would be the best optimized design. The second important parameter is the total heat flux obtained across the surface area of the fin body. Greater the heat flux better is the heat transfer characteristics. The results that are obtained for the various profiles discussed in chapter 3 are plotted below in section 5.2.  

B. CAE - Results of the Various Compressor fin Body Model at a Glance.

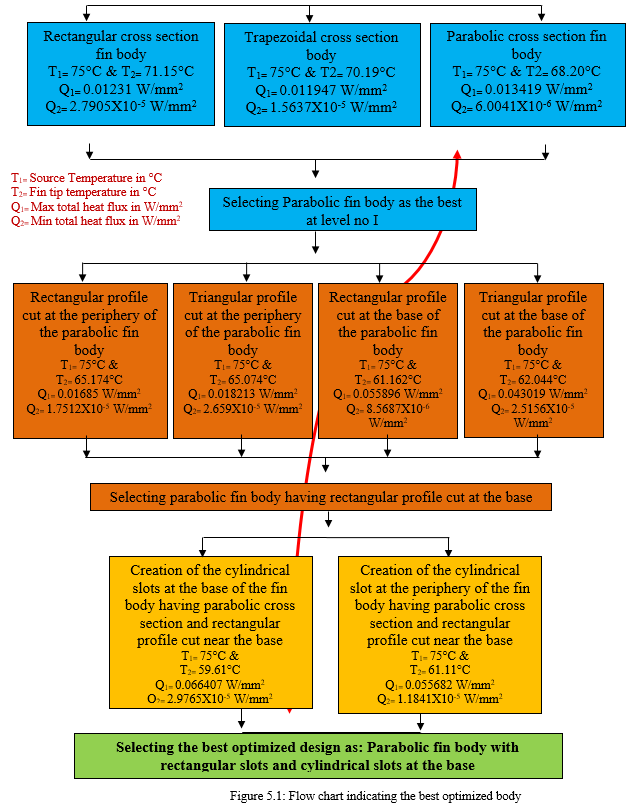
C. Discussion

1. In the complete project due the specific  constraint of the 3D model and the actual assembly conditions that are present, the  only parameter that is consider for improving the maximum heat transfer is the cross section of the fin and the surface area of the fin.
2. In level I design analysis is done on cross section area such as rectangular, trapezoidal and parabolic. The results show that most optimized fin is the parabolic one.
3. The parabolic curve has more heat dissipating area for the same length of the fin.
4. The temperature gradient (?t) that is obtained between the source temperature and the tip of the fin is highest in the parabolic fin body i.e. 75°C -68.20°C = 6.8°C
5. The second highest temperature gradient (?t) that is obtained is that of the trapezoidal fin body i.e. 75°C -70.19°C =4.81°C.
6. The third highest gradient (?t) that is obtained is that of the rectangular fin body i.e. 75°C -71.15 = 3.85°C
7. The ascending order of the ideal heat dissipating fin bodies can be stated as a) parabolic fin body b) trapezoidal fin body c) rectangular fin body.
8. Selecting parabolic fin body as the best and optimized one at level I is done on the above obtained results.
9. Four different options are considered at level II design, i.e.

• Rectangular profile cut at the periphery of the parabolic fin body.
• Triangular profile cut at the periphery of the parabolic fin body.
•  Rectangular profile cut at the base of the parabolic fin body.
• Triangular profile cut at the base of the parabolic fin body.

The rectangular profile cut at the base of the parabolic curve gives the highest temperature gradient ?t = 75°C -61.762°C = 13.838 °C

• The area kept on the fin and the cut must be proportional, hence 50% in profile cut and rest 50 remaining on the base of the fin is kept as the best option for obtaining the maximum heat transfer as well as for proving good strength.
• Triangular profile at the base of the tip will definitely leave more material at the base of the tip as compared   to fin body having rectangular cut at the base. This will allow the fin to take maximum heat transfer and give maximum temperature gradient (?t), hence selecting parabolic curve with rectangular slot at the base as the best optimized fin body at level II.
• Further improvement in the temperature gradient (?t) can be done  which will take care of the strength as well provide maximum heat transfer is done at level  III
• At level III circular slots of diameter 8mm are made at 62.00mm PCD and at 38.00mm PCD respectively. The 62.00mm PCD appears at the periphery side where as the 38.00mm appears on the base side.
• Results shows that the circular slots at the base of the fin shows the highest temperature gradient(?t) 75°C -59.61°C = 15.39 °C

VI.   FUTURE SCOPE

Since in the complete design sets, the size of the overall envelope of the fins body remains constant. In the analysis that is performed in complete design sets the variation of the body dimensions are not done. If the body dimensions are changed then there is a scope revisiting the body shapes, profile cuts that are made over the complete body which will lead exploring new parameters explored.

VII. ACKNOWLEDGEMENT

I sincerely express my deep sense of gratitude to my guide, Prof. Onkar G. Sonare, Department of Mechanical Engineering for his valuable guidance and encouragement during the course of this work. I wish my sincere thanks to Dr. P. D Deshmukh, Head of Mechanical Engineering Department for his valuable guidance.

I am also thankful to Prof. (Dr.) S. D. Sawarkar, Principal and other staff member of Mechanical Engineering Department who are involved in making this part of the project successful.

Lastly, this project would not have been accomplished without help and moral support from my family and friends and I remain profoundly grateful for their contribution in my growth and development.                                     

Conclusion

The results that are plotted in Ansys shows that fin body having parabolic cross section with rectangular profile slots at the base in combination with circular holes at the base are the best optimized design in all design sets.

References

[1] P. Ragupati, Dr V. R. Sivakumar, “Enhancing heat removal by optimizing fin configuration in air compressor,” Journal of Engineering science and Research Technology, ISSN 2277-9655, May-2014 [2] Sp. G. Pantelakis, N. D. Alexopoulos, A. N. Chamos, “Mechanical Performance Evaluation of Cast Magnesium Alloys for Automotive and Aeronautical Applications”, Journal of Engineering and Technology, 422 / Vol. 129, July 2007. [3] Avedesian, M., and Baker, “Magnesium and Magnesium Alloys”, ASM Specialty Handbook, ASM International, Metals Park, OH. [4] Davis, J. R., 1993, “Aluminum and Aluminum Alloys,” ASM Specialty Handbook, ASM International, Metals Park, OH. [5] Alexopoulos, N. D., and Pantelakis, Sp. G. , “Evaluation of the Effects of Variations in Chemical Composition on the Quality of Al–Si–Mg, Al–Cu, and Al–Zn–Mg Cast Aluminum Alloys,” Journal of Materials Engineering and Performance, 12(2), pp. 196–205, 2003 [6] S.Selvaraja, P.Venkataramaiah, “Design and Fabrication of an Injection Moulding Tool for Cam Bush with Baffle Cooling Channel and Submarine Gate” International Conference On Design And Manufacturing, IConDM 2013, Procedia Engineering 64, 1310 – 1319, 2013 [7] B. Vijaya Ramnath, C.Elanchezhian, Vishal Chandrasekhar, A. Arun Kumar, S.Mohamed Asif, G. Riyaz Mohamed, D. Vinodh Raj ,C .Suresh Kumar, B “Analysis and Optimization of Gating System for Commutator End Bracket”, 3rd International Conference on Materials Processing and Characterisation (ICMPC 2014). Procedia Materials Science 6, 1312 – 1328, 2014 [8] Esmail M.A. Mokheimer, “Performance of annular fins with different profiles subject to variable heat transfer coefficient, International” Elsevier, Journal of Heat and Mass Transfer 45, 3631–3642, 2002 [9] S. H. Barhatte, M. R. Chopade “Experimental and Computational Analysis and Optimization for Heat Transfer through Fins with Triangular Notch” International Journal of Emerging Technology and Advanced Engineering Website, ISSN 2250-2459, Volume 2, Issue 7, July 2012 [10] Sikindar Baba, Md Nagakishore.S, Prof.M.Bhagvanth Rao “Thermal Analysis on a Finned Tube Heat Exchanger of a Two Stage Air Compressor International Journal for research in applied science and engineering technology, IJRASET Volume 2 Issue V, ISSN: 2321-9653, May 2014 [11] Bejan A. and Morega A. M., “Optimal Arrays of Pin Fins and Plate Fins in Laminar Forced Convection”, J. Heat Transfer, Volume 115, pp. 75-81. [12] Barhatte. S. H, Chopade. M. R, Kapatkar V. N, “Experimental and Computational Analysis and Optimization for Heat Transfer through Fins with different types of Notches”, Journal of Engineering Research and Studies, Volume II, Issue I, January-March 2011. [13] Poulikakos, A. and Bejan, A., “Fin Geometry for Minimum Entropy Generation in Forced Convection” ASME Journal of Heat Transfer, Volume 104, pp. 616-623. [14] W. W. Lin and D. J. Lee, “Second-law analysis on a flat plate-fin array under cross flow” International Communications in Heat and Mass Transfer, Volume 27, Issue 2, February 2000. [15] Islam Md. Didarul, Oyakawa Kenyu, Yaga Minoru and Senaha Izuru, “Study on heat transfer and fluid flow characteristics with short rectangular plate fin of different pattern” Experimental Thermal and Fluid Science, Volume 31, Issue 4, February 2007. [16] P. R. Kulkarni, “Natural Convection heat transfer from horizontal rectangular fin arrays with triangular notch at the center.” Paper presented at NCSRT-2005. Nov 18-19, 2005, Pg. No.: 241-244. [17] Yunus A. Çengel, 2004, “Heat Transfer- A Practical Approach”, SI units 2nd Edition, Tata McGraw Hill Co., Pg. No. : 156-168, 333-352 & 459-500 [18] P. K. Nag, 2006, “Heat & Mass Transfer”, 2nd Edition, Tata McGraw Hill Co. Pg. No. : 86-108 & 425-449 [19] Y. A. Çengel, “Heat Transfer- a Practical Approach”, SI units 2nd Edition, Tata McGraw Hill, pp. 240-275, 2004. [20] F. P. Incropera, D. P. DeWitt, “Fundamentals of heat and mass transfer”, 4th Edition, John Wiley & Sons, ISBN 100.07.06.345376, pp. 147-172, 1996. [21] B. Senol, S. Mecit, and O. Murat, “Parametric study of natural convection heat transfer from horizontal rectangular fin arrays”, International Journal of Thermal Science, 39, pp. 797–805, 2006. [22] D. Soodphakdee, M. Behnia, and D. Copeland, “A comparison of fin geometries for heat sinks in laminar forced convection: part1- Round, elliptical and plate fins in staggered and In-line con Figure rations”, International Journal of Microcircuits and Electronic Packaging, pp. 3510-3517, 2001. [23] M. Christensen, “Static Heat Transfer analysis of Fins”, Department of Mechanical Engineering, The University of British Columbia, pp. 2-10, 2004. [24] S. S. Sane, N. K. Sane, G. V. Parishwad, “Computational analysis of horizontal rectangular notched arrays dissipating heat by natural convection”, 5th European Thermal-Sciences Conference, The Netherlands, pp. 126-133, 2008. [25] B. Yazicioglu, and Yuncu, “A Correlation for Optimum Fin Spacing Of Vertically-Based Rectangular Fin Arrays Subjected To Natural Convection Heat Transfer”, Journal of Thermal Science and Technology, pp. 99-105, 2009 [26] M. J. Sable, S. J. Jagtap, P. S. Patil, P. R. Baviskar, S. B. Barve, “Enhancement of natural convection heat transfer on vertical heated plate by multiple v-fin arrays”, International Journal on Heat and Mass Transfer, 2010, pp. 123-128. [27] S. V. Naidu, V. Dharma Rao, B. Govinda Rao, A. Sombabu, and B. Sreenivasulu, “Natural convection heat transfer from fin arrays-experimental and theoretical study on effect of inclination of base on heat transfer”, ARPN Journal of Engineering and Applied Sciences. Vol. 5, NO. 9, pp. 7-15, 2010 [28] M.V.Matkar, Thermal Analysis of Copper Fin by FEA, pp. 1229-1236, 2011. [29] Dong-Kwon Kim, “Thermal optimization of plate-fin heat sinks with fins of variable thickness under natural convection”, International Journal of Heat and Mass Transfer, Department of Mechanical Engineering, Ajou University, Suwon, Republic of Korea, pp. 752-761, 2012. [30] S. S. Kharche, H. S. Farkade, “Heat transfer analysis through fin array by natural convection”, International Journal of Emerging Technology and Advanced Engineering , Volume 2, Issue 4, ISSN 2250-2459, pp. 595-598, 2012. [31] M. Mashud, Md. Ilias Inam, Zinat Rahman Arani and Afsanul Tanveer, “Experimental Investigation of Heat Transfer Characteristics of Cylindrical Fin with Different Grooves”, International Journal of Mechanical & Mechatronics Engineering IJMME Vol. 9, No: 10, pp. 40-45, 2011. [32] Guei-Jang Huang, Shwin-Chung Wong, “Dynamic characteristics of natural convection from horizontal rectangular fin arrays”, International Journal of Applied Thermal Engineering, Department of Power Mechanical Engineering, National Tsing Hua University, Hsin-Chu 300, Taiwan, ROC, pp. 81-89, 2012. [33] S. D. Suryawanshi, N. K. Sane, “Natural Convection Heat Transfer from Horizontal Rectangular Inverted Notched Fin Array”, ASME Journal of Heat Transfer, Vol. 131, Issue 8, pp. 29-42, 2009. [34] S. D. Suryawanshi, N. K. Sane, A. A. Kulkarni, “Parametric Study of Rectangular Inverted Notched Fin Arrays in Natural Convection Heat Transfer”, International Journal of Computing and Applications Vol. 4 No. 2, pp. 1-14, 2009. [35] N. K. Sane and S. D. Suryawanshi, “Natural Convection Heat Transfer from Horizontal Rectangular Inverted Notched Fin Arrays”, International Journal of Engineering Research and Industrial Applications, Volume. 2 No., VII, pp. 312-317, 2009. [36] A. B. Ganorkar, V. N. Kriplani, “Review of Heat transfer Enhancement in Different types of Extended Surfaces”, International Journal of Engineering Science and Technology, Vol. 3 No. 4, pp. 205-213, 2011. [37] S. K. Agrawal, R. Gauda, “Some experimental studies on heat transfer augmentation for flow of liquid through cicular tubes using twisted angles and tapes”, Department of Chemical Engineering, National Institute of Technology, Rourkela, pp. 185-192, 2008.

Copyright

Copyright © 2022 Suprit Narendra Modi, Dr. R. R. Jaware. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.