Optimization Techniques to Solve Travelling Salesman Problem Using Machine Learning Algorithms

Abstract

Travelling Salesmen problem is a very popular problem in the world of computer programming. It deals with the optimization of algorithms and an ever changing scenario as it gets more and more complex as the number of variables goes on increasing. The solutions which exist for this problem are optimal for a small and definite number of cases. One cannot take into consideration of the various factors which are included when this specific problem is tried to be solved for the real world where things change continuously. There is a need to adapt to these changes and find optimized solutions as the application goes on. The ability to adapt to any kind of data, whether static or ever-changing, understand and solve it is a quality that is shown by Machine Learning algorithms. As advances in Machine Learning take place, there has been quite a good amount of research for how to solve NP-hard problems using Machine Learning. This report is a survey to understand what types of machine algorithms can be used to solve with TSP. Different types of approaches like Ant Colony Optimization and Q-learning are explored and compared. Ant Colony Optimization uses the concept of ants following pheromone levels which lets them know where the most amount of food is. This is widely used for TSP problems where the path is with the most pheromone is chosen. Q-Learning is supposed to use the concept of awarding an agent when taking the right action for a state it is in and compounding those specific rewards. This is very much based on the exploiting concept where the agent keeps on learning on its own to maximize its own reward. This can be used for TSP where an agent will be rewarded for having a short path and will be rewarded more if the path chosen is the shortest.

Introduction

I. INTRODUCTION

In today’s day and age, a lot of online websites have started delivery from town to town or city based. It leads to many variations of traveling salesman’s problem, vehicle routing problem, job-shop scheduling problem, and more variants. These problems are classified as Combinatorial Optimization Problems. They are commonly found in domains like transportation, operations research, logistics, and telecommunications. The overall goal is to find an optimal solution, which can be modeled as a sequence of actions/decisions to maximize/minimize the objective function for a specific problem. However, as the scale of the problem grows, the time to find the optimal solution increases exponentially.

TSP is a non-deterministic polynomial-time hard (NP-hard) computational problem with no-known polynomial time solutions yet. There are still many questions open to be answered for the worst-case analysis of exact algorithms for NP-hard problems. Today, due to more research in the field of machine learning, we can compare some well-established machine learning algorithms such as Ant Colony Optimization and Q-learning.

II. LITERATURE SURVEY

III. TSP AND ALGORITHMS

A. Introduction

Traveling Salesman Problem (TSP) is a classical and most widely studied problem in Combinatorial Optimization. It has been studied intensively in both Operations Research and Computer Science since the 1950s as a result of which a large number of techniques were developed to solve this problem. Much of the work on TSP is not motivated by direct applications, but rather by the fact that it provides an ideal platform for the study of general methods that can be applied to a wide range of Discrete Optimization Problems. Indeed, numerous direct applications of TSP bring life to the research area and help to direct future work.

The idea of the problem is to find the shortest route of salesman starting from a given city, visiting n cities only once and finally arriving at origin city.

B. Different Approaches to solve TSP

There are two types of approaches to solving TSP.

One way is to use exact solvers, which implies getting the optimal solution every time by using methods like Interior Point, Branch-and-Bound, and Branch- and-cute. But these come at cost of huge run times, space requirements and are only viable for a fewer number of nodes.

Another way is to use non-exact solvers. These methods offer potentially non-optimal but typically faster solutions.  The way to get better results for solving TSP is to make these types of algorithms more optimized and being fast at the same time to get the ideal solution.

C. State of Art Algorithms

State of the Art heuristic approaches to solve TSP are Ant Colony Optimization and Q-Learning which will be discussed below.

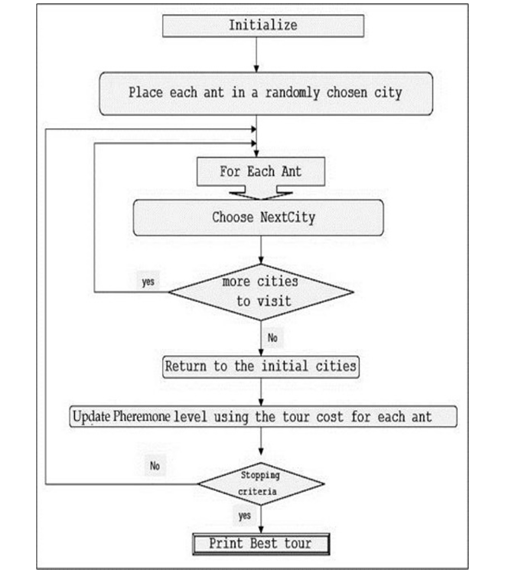
Figure 1: Flowchart of implementation of ACO for TSP

1. Ant Colony Optimization

Ant Colony Optimization is a heuristic algorithm that is inspired by examining ants and their movement. Ants cooperate to find resources by laying down a chemical on the ground called a pheromone for other ants to follow. The more amount of pheromone, the high probability the ants will follow that path. In this fashion, shorter routes to food sources get more amount of pheromone.

By using this phenomenon, researchers have devised an algorithm for optimizing different problems. One of the problems where it is applied is TSP. This algorithm uses the nearest-neighbor search and diffluence strategy.

1. Using ACO for TSP: The algorithm for implementing ACO for solving TSP is shown below in form of a flowchart. The ants are placed at random cities and are made to move to the next city by using a formula that uses the concepts of probability, the pheromone levels, and heuristic value. It donates the probability of ant k that is in city r to go in city s.

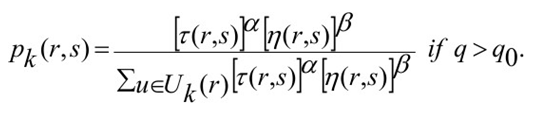
α denotes the importance of pheromone for the ant and β denotes the importance of heuristic values.

2. Drawbacks: This algorithm takes a lot of time for searching and is prone to be trapped in the local minima. Though ACO tries to prevent it by updating local rules, there are other ways to boost it’s performance using machine learning which are being researched.

E. Q-Learning

Q-Learning is a reinforcement learning algorithm that is used on agents for predicting an action for a state the agent is in. This algorithm specializes in maximizing the rewards the agent can get in the current and successive states.

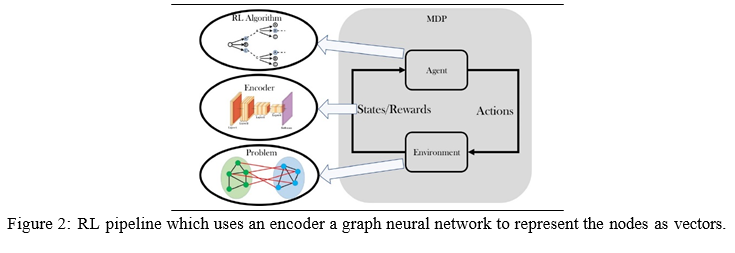
1. Using Q-Learning for TSP: The agent is placed at a random city and it takes action according to the Q-value function giving out different Q values. The Q- values are stored in a Q-Table which can be used to find the shortest path. We use a ? and a learning rate γ. By using the ?-greedy approach, if the ? has the greater value, a city is randomly selected, otherwise using the nearest neighbor. This gives an immediate reward to the agent which makes it adjust its Q-values and checks if the tour length was the shortest from the beginning. If it is found, the rewards are updated by themselves, and the agents are given a reward to the ones who belong to that shortest tour. Then the global minimum tour is constructed by using the Q-values. RL needs a setup of environment enabled with an encoder/decoder system to take necessary actions according to its states. The diagram of an example pipeline is given above [Fig 2].

This algorithm is really useful when applying for different variations of the problem like TSP with refueling(TSPWR). The algorithm from the Ottoni’s paper[] is given above[Fig3] .

2. Benefits

a) Easier to implement various variations like Fueling and time limitations.

b) Self-learning and can be used to handle larger scale problems.

c)Can be used to improve itself over time in a longer duration.

3. Drawbacks

a. Tuning RL parameters are quite hard.

b. Simulating and understanding how the algorithm is behaving to optimize is can get very complex.

c. It needs a lot of testing for real world applications against very quick and drastic changes.

F. Experimental results

After discussing the working of the algorithm, here are a few experimental results of the same. The algorithms are compared with other popular methods to solve TSP like Nearest Neighbour and Genetic Algorithm and the Optimal time has been given as well. The instances are from several TSPLIB instances for which the solutions are already given. The results are presented as the best out of 15 trials. As one can see, Q-Learning comes quite close to the optimal values and can be improved with additional research and work. As the number of cities increases, ACO and QL remains the nearest ones to the optimal value.

IV. APPLICATIONS

There are many applications for TSP and by using these algorithms, we can solve TSP with different variations. Here are a few applications:

A. Maps application considering time rejection and fuel.

B. Delivery Applications like food delivery or parcels where food hotness and delivery time are a few variables to be considered.

C. Logistics applications.

D. Planning and scheduling.

E. Manufacturing microchips where the robot has to go from one point to another to solder components.

F. Astronomy where telescopes are used, where the telescope has to go from one point to another in minimum time and different variables.

Conclusion

Machine learning can help us solve different complex problems included Combinatorial Optimization Problems. The algorithms derived are very useful where heuristic results. that is, results which are fast and near-optimal solutions are sufficient. As we studied through two most promising heuristic algorithms, we can notice that both of them are quite promising and can be improved if more research is done for the same. ACO can really benefit from machine learning as seen in Yuan Sun’s paper [6]. Q-Learning is relatively newer, is still going through a vigorous study by machine learning scientists, and takes a lot of time and trial and error to fine-tune. This can be improved much more in the future to get better results. For the future, more variables can be introduced like Fuel + Time or traffic to see whether these algorithms can perform well there as well.

References

[1] Nina Mazyavkina, Reinforcement Learning for Combinatorial Optimization. [2] Rongkai Zhang, Deep Reinforcement Learning for Travelling Salesman Problem with Time Rejection Windows.DOI: 10.1109/IJCNN48605.2020.9207026 [3] Jeremiah Ishaya,A comparative analysis of the traveling salesman problem: Exact and machine learning techniques.DOI:10.30538/psrp-odam2019.0020 [4] Andr´e L. C. Ottoni,Erivelton G. Nepomuceno,Marcos S. de Oliveira,Daniela C. ,R. de Oliveira, Reinforcement learning for the traveling salesman problem with refueling.DOI:10.1007/s40747-021-00444-4 [5] Yuan Sun, Sheng Wang, Yunzhuang Shen, Xiaodong Li, Andreas T. Ernst, Michael Kirley, Boosting Ant Colony Optimization via Solution Prediction and Machine Learning

Copyright

Copyright © 2022 Prince Nathan S, Onkar Saudagar , Rutika Shinde. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.