An Overview of the Ancient Indian Vedic Mathematics Techniques

Abstract

This study examined at how Vedic Mathematics solves basic math problems using Vedic Mathematics. The ancient approach of Indian mathematics is known as Vedic mathematics. It employs a one-of-a-kind computation method based on the 16 sutras and 13 sub-sutras including a variety of modern mathematical problems such as trigonometry, arithmetic, geometry, factorization, quadratic equations, and calculus. This study summarizes some important sutras from Vedic mathematics with examples. Additionally, we highlight some recent applications of Vedic mathematics from existing literature.

Introduction

I. INTRODUCTION

Vedic Mathematics arose in India more than two thousand years ago, shortly after the invention of the number system. Vedic mathematics was developed and taught in the form of Sutras in the Rig Veda throughout ancient times. This Vedic mathematics simplifies calculations in the context of large numbers. Perhaps astrological and astronomical computations were performed in ancient times using this Vedic Mathematics. Shree Jagad Guru Bharti Krishna Tirthji Maharaj was the founder of Vedic mathematics, who discovered the sixteen sutras of mathematics between 1911 and 1918. During those six years, Shree Garuda compiled those sutras from the Atharva Vedas, an ancient Indian calculating system. These sixteen sutras are now known as Vedic mathematics. These sutras are drawn from the Ganit Sutras, which are popular as a simple mathematical system, or from the Shulabh Sutras [1].

Vedic mathematics simplifies calculations in the context of large numbers. Perhaps astrological and astronomical computations were performed in ancient times using this Vedic Mathematics addition, multiplication, divisibility, square and cube roots, auxiliary fractions, and complex numbers are all simplified by Vedic mathematics. It gives answers in a single line by skipping numerous steps in traditional maths.

Raikhola, Panthi, Acharya, and Jha [2] conclude in their study that Vedic Math is more streamlined, unified, and speedier than the standard system. They find the significance of the Vedic techniques as follows:

1. Vedic Math provides flexibility, enjoyment, and enormous gratification, transforming a dull topic into a delightful one that anybody can acquire knowledge with a smile.
2. Vedic Math, with its unique qualities, has the ability to alleviate the intellectual issue of mathematical concern.
3. Vedic techniques boosts both the speed and accuracy of the calculations. Vedic mathematics provides mental, one-line, and super-fast procedures and rapid cross-checking systems.
4. Vedic sutras give a complementary, transparent, and basic mathematical system.
5. The development of the Vedic mathematics approach is a remarkable and intriguing invention that has led to numerous applications in all areas.

Mandloi [3] discussed that Vedic sutras allow a human being to answer mathematical questions more quickly. It aids in the decision-making process for both basic and difficult challenges. Further, it alleviates the load of remembering tough topics and improves a person's concentration and motivation to learn and grow his talents.

Sharma, Khubnan and Subramanyam, [4] provided a variety of advancements and developments in the subject of Vedic maths, with a goal of the formation of multipliers and algorithms such as the algorithms of Urdhva Tiriyagbhyam and Nikhilam, etc. In combination with NEP2020, they also give an overview of Vedic Mathematics.

Priya, Goel, and Kumar [5] present Vedic sutras for elementary calculus with examples. Parajuli [6] compared the results of Vedic sutras with the conventional techniques for elementary algebraic equations. Chauhan and Ali [1] discussed Vedic sutras in the context of multiplication only.

As far as we know, no research exists in the literature in which the three-topic covered in a single study. In this paper, we discuss the Vedic sutra for each case of simple calculations, algebra, and for calculus.

The remainder of the article is as follows:   Section II provides the use of Vedic mathematics in different disciplines like elementary calculations, Elementary Algebra, and elementary calculus. In section III we highlight the modern application based on Vedic Mathematics Techniques. The conclusion has been presented in Section IV.

II. USE OF VEDIC MATHEMATICS IN DIFFERENT DISCIPLINES

In this section, we discuss some important sutras from Vedic mathematics which are helpful in easy calculations and implementation in applications. First, we list the 16 sutras with sub-sutras and then find the use of some sutras in calculations, algebra, and calculus. The name of these sutras as follows sutras and subsutras [7] :

1. Ekadhikina Purvena (Sub sutra-Anurupyena) Its meaning is “By one more than the preceding one   (proportionality)”.
2.  Nikhilam Navatashcaramam Dashatah (Sub sutra: Sisyate Sesasamjnah) All of them are from 9 and the last one is from 10. (Remainder remains constant).
3. Urdhva-Tiryagbyha(Sub sutra:Adyamadyenantya-mantye-na) Vertically and crosswise (First to last and last to first).
4. Paraavartya Yojayet (Sub sutra: Kevalaih Saptakam Gunyat) Transpose and adjust (The multiplicand for 7 is 143.)
5. Shunyam Saamyasamuccaye (Sub sutra: Vestanam) When the sum is equal  that sum is zero (Using Osculation)
6. Anurupye Shunyamanyat (Sub sutra:Yavadunam Tavadunam) If one variable is in same ratio, the other variable is zero (Lesser due to a deficiency)
7. Sankalana-vyavakalanabhyam(Sub sutra:Yavadunam Tavadunam Varga) By addition and by subtraction 8. (Whatever the shortage, multiply it by the amount and square it.)
8. Puranapuranabyham (Sub sutra: Antyayordashake) By the completion or non-completion (Last Totalling 10)
9. Chalana-Kalanabyham (Sub sutra: Antyayoreva) Differences and Similarities (only the last terms)
10. Yaavadunam (Sub sutra: Samuccayagunitah) Whatever the extent of its deficiency (The addition of the coefficients in the product).
11.  Vyashtisamanstih(Sub sutra: Lopanasthapanabhyam) Part and Whole (By Alternate Elimination and Retention)
12. Shesanyankena Charamena (Sub sutra: Vilokanam) The remainders by the last digit (By Mere Observation)
13. Sopaantyadvayamantyam(Subsutra:Samuccayagunitah) The ultimate and twice the penultimate (The Product of the Sum is the Sum of the Products)
14. Ekanyunena Purvena: This sutras states “By one less than the previous one “.
15. Gunitasamuchyah: This sutra means that the multiplication of the sum is equal to the sum of the product
16.  Gunakasamuchyah: This sutra states that the additions of the factors is equal to the sum of the factors

 The following subsections show some numerical implementations of the above sutras.

A. Application of Vedic Formulas in Elementary calculations

1. Ekadhikina Purvena

Ekhadhikina Purvena is a powerful sutra useful for finding the squares of numbers and special divisions like 1 divided by a number e.g.: 9,19, 29, etc. It is difficult to divide 1 by integers ending in 9 using the traditional approach, such as 19, 29, and 39. This is because some of these are prime numbers and hence cannot be factored in. We use the sutra Ekadhikena Purvena to reduce such laborious procedures as well as errors.

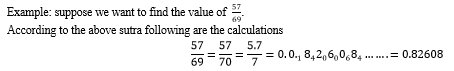
2. Nikhilam Navatashcaramam Dashatah

This approach is used to multiply numbers that are near to the power of ten. All from 9 and last from 10 is the English translation. The powers of ten from which the difference is determined are referred to as the Base. These numbers serve as references to determine whether the number is more or less than the base. The distinctions in these circumstances are termed excesses and deficiencies.

Example: The value of 95*96=9120

3. Urdhva-Tiryagbyham:

Urdhva Tiryagbyham is a shortcut method/ Sutra 3 for the multiplication of all types of numbers in Vedic Mathematics. The English translation for the same is Vertically and Cross-wise. For numbers up to 3 digits, we can easily use the normal process of this method.

Example: suppose we want to multiply two numbers 68 and 37.

For the multiplication result on the unit place, the value will be from the multiplication of two last digits and 7 which is 56 so unit place there will be 6 with 5 left the cross multiplies the digits and find the sum which is (42+24 =66) so on tens place digit is 1 (66+5-=71) and finally, the multiplication of first digit numbers is 18, (18+7) 25 will be taken as the remaining number. So, 68*37=2516.

4. Antyoyedashake

This is also one of the Vedic Mathematics sutras for easy multiplication. To follow this sutra, the sum of the multiplier's last two digits must be equal to 10.

Example: Suppose we want to multiply 92 by 98. We find multiplication (9+1) 10 by 9 and multiplication of the last two digits 2 and 8 and write the multiplication of 92 and 98 as 9016.

B. Application of Vedic Formulas in Elementary algebra

Numerous Vedic formulas can be utilized to solve algebraic issues [6]. This study does not contain all the Vedic techniques. Only some relevant algebraic operations have been chosen.

1)  Anurupye Shunyamanyat

This Sutra is used to solve a particular type of simultaneous equation in which the coefficients of a variable are in the same ratio to the other variable [7].  In such examples, this formula states that the 'other' variable is zero, from which we have two simple equations in the first variable (previously taken) that, of course, provide the same result for the variable.

Example: 5x + 12y = 6 & 3x + 36y = 18. The y-coefficient are in the ratio 12:36 = 1:3, the ratio of the constants is 6:18 = 1:3. Hence putting other variables x = 0 in any one of the above equations we get y=6/12 and x=0.

2)  Paravartya Yojayet

The Paravartya Yojayet is very close to the Remainder Theorem and the Horner process of synthetic division in terms of algebraic division. Horner's synthetic division technique is merely one component of the Paravartya formula, which can be extended to situations where the divisor is quadratic, cubic, or any size polynomial [6].  By adding RHS and LHS under distinct types of headings, the Paravartya sutra can be employed for specific forms of equations. If the sum of the numerators on the LHS equals the single numerator on the RHS.

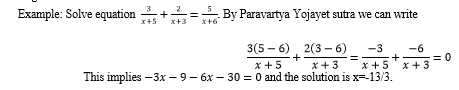
3)  Gunakasamuchyah

The English meaning is the factors of the sum is equal to the sum of the factors means. The sum of the coefficients in the factors equals the sum of the coefficients in the product.

Example:x+1x+4=x2+5x+4   

1+11+4=1+5+4=10

???????C. Application of Vedic Formulas in Elementary calculus

The most significant mathematical achievement is the evolution of the Calculus and Integral Calculus [5]. Differential Calculus is useful in a wide range of real-world situations that demand us to determine the rate of increase or decrease of one variable. Some Sutra for integration and differentiation are as follows

???????III. APPLICATION OF VEDIC MATHEMATICS IN MODERN TIME

Real-world applications, such as managing environmental issues, necessitate a rapid response from the processor to process the obtained information. The multiplier is a crucial component of both signal processing and digital computer systems. Multipliers have a big surface area, a very long latency, and high-electric consumption [7]. As a result, good multiplier architecture boosts a system's efficiency and performance. One example of a high-speed, low-area multiplier architecture is the Vedic multiplier. Vedic techniques teach the fundamentals of fast multiplication. Jie and Ruslan [8] introduced a 2x2-bit multiplier using a 1-bit hybrid full adder with 13 transistors based on vedic technique. They compare performance characteristics like power consumption and response time to existing designs.  Gaikwad and Chavan [9] present a brief review of the Vedic techniques in Digital Signal Processing Operations.

They demonstrate how Vedic mathematics can be applied for fast signal processing. Multipliers can be utilized to reduce power consumption, faster speed, less complexity, and area, among other things by using the techniques of Vedic mathematics. Vedic mathematical methods can be shown to be more efficient than traditional methods in FIR and IIR filters for producing effective outcomes in biomedical signal de-noising. Reddy [10] focuses on square architecture based on the Anurupya Sutra. Their proposed method is an efficient way for dividing a large magnitude number into smaller magnitude numbers and concatenating the smaller magnitude numbers. Senthilkumar [11] presents the application of Vedic multiplier (based on Vedic mathematics algorithm) in biomedical diagnosis which could be a signal or image processor. Shumathi and Indumathi [12] proposed a strategy for detecting breast cancer using the technique of image-processing combined with Vedic sutras in this paper. The primary goal of this work is to help pathologists enhance their accuracy and efficiency in detecting cancer grade, as well as to reduce inter-observer variation. Mandal and Dasgupta [13] describe an application that uses Vedic Math to mathematical calculations on our calculator. They created a user interface for Vedic products and Vedic sum in a calculator made for Android-based smartphones in their proposed application. With the help of Vedic techniques, this program minimizes the complexity of mathematical calculations. Kahar [14] used Urdhva Tiryagbhyam Sutra to fast the speed of the Vedic multiplier. Research by Lavanya and Kalaiselvi [15] shows how Vedic beliefs may be used to develop an Adaptive FIR filter, which is employed in RADAR for weak signal detection. Nanthakumar [16] provides some instances to demonstrate the supremacy of Vedic Mathematics in numerical calculations. To construct efficient cryptographic arithmetic primitives, Kumar and Rai [17] merged reversible logic and Vedic mathematics. The implementation and synthesis have identified significant improvements in performance characteristics like as area, power dissipation, and delay.

The studies mentioned above show that Vedic Mathematics techniques dramatically reduced the computing time of basic mathematical operations. When compared to traditional methods, using Vedic Mathematics basic operations consumes less memory and power because fewer computations are required. The impression of Vedic methodologies that were previously inculcated or integrated into modern mathematical systems, such as Crammer's rule, Horner's synthetic division method, Remainder theorem of polynomials, factorizations of polynomials, cross multiplication method to solve simultaneous equations, partial fractions of proper and improper functions. Except in a few situations, conventional mathematicians are completely unaware of many of the Vedic formulas described in this paper. Even so, there are substantial restrictions to Vedic formulas in particular circumstances involving very basic algebraic solutions.

Conclusion

In this report, we look at the sutras, which are the most useful laws of Vedic Mathematics with applications in fields such as algebra, arithmetic, geometry, and calculus, and we provide instances of these sutras. Given the preceding sutras, we can conclude that Vedic mathematics is a promising methodology in terms of area of application, speed and possibly power as well. Furthermore, Vedic mathematics methods can be acquired with low effort and in a short period of time, making them appealing alternatives for calculations in a variety of modern competitive tests. Mathematics can be made simple and enjoyable by employing the strategies recited in Vedic mathematics. It is simpler and more beneficial for students to solve multiplication problems. In other words, there are several mystical formulas for converting kilometers (Km) into meters, meters into Km, Km into miles, kilos into pounds and Fahrenheit into Celsius. As a result, we have more efficient formulas for transforming each magic calculation. We believe that the present work can be enjoyed by readers by using easy approaches in Vedic Mathematics when compared to modern textbook methods. The reader also contrasts the distinctions between Vedic Mathematics and Modern Mathematics.

References

[1] K.S. Chauhan, and M.F Ali, “Difference between Vedic Mathematics and Modern Mathematics in Multiplication Algorithm,” International Journal of Engineering Research in Current Trends vol,3 pp, 4-6 June 2021. [2] S.S.Raikhola, and V Campus, “ A Thematic Analysis on Vedic Mathematics and Its Importance,” Open Access Library Journal, vol. 7(08), pp 1-9, August 2020. [3] A Mandloi, “Comparative Analysis of Techniques of Vedic Mathematics” International Journal of Mathematics Trends and Technology, vol 68 pp.30-32, April 2022. [4] T. Sharma, R.Khubnani, and C. Subramanyam,. “Study of mathematics through Indian Veda’s: A review,” Journal of Physics: Conference Series vol. 2332, pp.012006, September 2022. [5] D.Priya, P.Goel, and A.Kumar, “Vedic mathematics in derivatives and integration, differential equations and partial differential equations,” Journal of Mathematical Problems, Equations, and Statistics, vol 2, pp 27-32, June 2021. [6] K.K. Parajuli, “Elementary Algebra on Vedic Mathematics,” Mathematics Education Forum Chitwan, vol. 6, pp. 82-94, December 2021. [7] S. Shembalkar, S. Dhole, T. Yadav, and P. Thakre, “Vedic Mathematics Sutras-A Review”. International Conference on Recent Trends in Engineering Science and Technology,vol 4, p.3, 2017. [8] S.J. Lee and SH Ruslan, “A 2x2 Bit Multiplier Using Hybrid 13T Full Adder with Vedic Mathematics Method,” International Journal of Integrated Engineering, vol 20(3), July 2018. [9] K.M. Gaikwad, and M.S.Chavan, “Vedic mathematics for digital signal processing operations: a review,” International Journal of Computer Applications, vol 113(18), 2015. [10] B.N.K. Reddy, “Design and implementation of high-performance and area-efficient square architecture using Vedic Mathematics”. Analog integrated circuits and signal processing, vol 102(3), pp.501-506 2020. [11] Senthilkumar, V.M., Ravindrakumar, S., Nithya, D. and Kousik, N.V., 2019. A Vedic mathematics-based processor core for discrete wavelet transform using FinFET and CNTFET technology for biomedical signal processing. Microprocessors and Microsystems, 71, p.102875. [12] R. Sumathi, and R. Indumathi, “An Effective Automatic Breast Cancer Identification using Vedic Mathematics,” Materials Today: Proceedings, vol 47, pp. 247-250, 2021. [13] L. Mandal, and K. Dasgupta, “Use of Vedic Mathematics to Speed-up Basic Mathematical Operations in Android Based Calculator,” IEEE International Conference on Intelligent Sustainable Systems (ICISS) pp. 162-165, IEEE February 2019. [14] D.K. Kahar, and H. Mehta, “High speed vedic multiplier used vedic mathematics”. IEEE International Conference on Intelligent Computing and Control Systems (ICICCS) pp. 356-359. June 2017. [15] M. Lavanya,and A. Kalaiselvi, “High speed FIR adaptive filter for RADAR applications.” IEEE International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET) pp. 2118-2122, March 2016. [16] A. Nanthakumar, “Vedic Mathematics and its applications.” Technological Advances in Science, Medicine and Engineering Conference June 2021. [17] V.G. Kiran Kumar, and C. Shantharama Rai, “Efficient implementation of cryptographic arithmetic primitives using reversible logic and Vedic mathematics,”. Journal of The Institution of Engineers (India): Series B, vol 102(1), pp.59-74 2021.

Copyright

Copyright © 2022 Reenu Kumari. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.