Performance Analysis of Synchronous Reluctance Generator

Abstract

The synchronous reluctance generators are a species of self-excited generators such as the induction generators. The self-excited synchronous reluctance generator (SynRG) has become a promising and viable replacement of self-excited induction generator because of the supply frequency dependence on the prime speed and not load. The self-excited synchronous reluctance generator has high reliability, low cost and robustness and capacity of variable speed operation. The aim of this research is to carry out performance analysis of shunt connected three-phase synchronous reluctance generator feeding an R-L load. The dynamic analysis is based on the classical d-q model where equations for electrical quantities were derived and implemented using a computer simulation tool, MATLAB®. The equations for steady state analysis were derived from the dynamic equations by setting all time variables to zero. The dynamic analysis was carried out on a 4-pole, speed of 1500 rpm with connected load at a fixed excitation capacitor value of 50uF for a 2.5kVA machine. Effect of excitation-capacitance variation and loading-conditions variation on the generated output voltage and frequency are presented and discussed. The load variations were done based on energy-current perturbation at a fixed power factor of 1.0. The load variations were done at several points and result shows that with the variations in the connected loads, the output frequency of the synchronous reluctance generator remains constant, which makes it a good alternative for induction generator. On the steady state analysis, it was discovered that on increasing the excitation capacitor, the terminal voltage increases as well as the output power. The result specifically revealed that when the capacitance increases from 25uF to 45uF, the terminal voltage and the output power increases from 200volts to 300volts; and 200watt to 1700watt. Therefore, it is recommended that to ensure machine excitation, the capacitor should not be reduced below a certain value. The study is beneficial for operation of an isolated power supply.

Introduction

I. INTRODUCTION

Electrical machines are devices that are used to make work easy. There are two major types of electrical machines by operation namely the static machine (transformer) and the rotating machines (the motors and the generators). Electrical motors convert electrical energy to mechanical energy while generators convert mechanical energy to electrical energy (Okoro, et al., 2006). Electric motors are widely used in the industries for lifting of mechanical loads while electric generators are widely used in electric power plant for power generation.

Electric generators can be classified into two namely the alternating current (AC) generators and direct current (DC) generators. The DC generators where first used in the 1930s before the supply distribution standard was changed from DC to AC (Adkins,1957) and (Fitzgerald,1990). The use of DC machines for power generation involves the brushed type and the brushless generator. The conventional brushed DC machine type is the machine which is furnished with carbon brushes and special device-a mechanical commutation, which convert alternating current into direct current under certain condition. The involvement of brushes in the construction of the DC machine requires cost for regular maintenance of the machine to increase its efficiency and reliability and also increase its life span. To get rid of the maintenance cost, the brushless DC machine was developed with the use of power electronic devices for the excitation of the field winding. But then, DC generators are mainly used in self-contained systems such as airplanes, automobiles, sub-marines etc., as primary source of power. Modern power design generation requires practically three phase AC generations. Therefore, DC machines are not used in most applications in industries, particularly in the electric power sector for power generation.

AC generator also called alternator can further be classified as induction and synchronous generators. The induction or asynchronous machine is widely called the workhouse of industries due to the fact that it is simple and rugged in construction, which gives it an inherently high reliability and robustness. But in terms of power generation, the induction machine has lower power factor, lower power density and lower efficiency than synchronous generator (Sadarangani, 2000). The power factor drops with higher pole numbers due to an increased leakage inductance (Say, 1948).

And the induction generator is not self-sustaining: It has to use lagging reactive power from synchronous machine and/or bank of capacitors to convert its mechanical energy to electrical energy. Again, the speed control of induction generator is complicated and difficult. For example, in order to control a doubly fed induction generator (DFIG), the rotor current needs to be controlled by a power electronic converter (Peterson, 2005) and (Chuong, 2015). However, both magnitude and frequency of the output voltage and current are load dependent, which makes performance prediction difficult and complicates the control strategy (Peter et al, 1989), (Chan 2005).

The synchronous generator is one of the first and most well-known synchronous machine types in terms of power generation. It was in the beginning common in MW-size power range, but is nowadays mainly used for different power range machines. Unlike induction machines in which the power factor is affected by their number of poles, the synchronous machines are not affected in the same manner by their number of poles. The synchronous machines have still a number of advantages which makes them very interesting. This includes: High efficiency, robustness and good controllability. It is therefore being expected that the synchronous generator will continue to play an important role, also in the future (Miller, 1986).

High speed synchronous generator driven by steam turbines differ considerably in their construction from the slow engine-driven machines and are often described as “flywheel-type”. There are two basic constructions: Machines with a cylindrical rotor and machines with a salient-pole rotor. For mechanical reasons, the cylindrical rotor is preferred for two poles machines because of the large centrifugal forces that arise. The salient-pole rotor is usually the more efficient solution for machines with four poles and upwards, both for cost reasons and performance reasons. The rotor can be made of either laminated steel or solid iron. The solid iron rotor is the dominating solution for machines with low pole numbers, because of its robust mechanical properties. This is the machine type that is studied in this work. For machines of higher pole number, a laminated core is often used. Cylindrical rotor is used for high speed applications while salient-pole rotor is used for low speed applications. The traditional applications for salient-pole machines are pump systems, paper mills, ship propulsion and other applications with moderate dynamic requirements.

In terms of rotor excitation winding, the synchronous generator mainly has the wound rotor synchronous generator (WRSG) type and the permanent magnet synchronous generator (PMSG) type as shown in Figure 1.1. The WRSG which is electrically excited type. Though the generator is simple and robust in structure with very low price compared to PM synchronous generator, WRSG generator has high copper losses in the rotor (due to additional rotor windings), lower efficiency, lower power density and less reliability compared to its PM synchronous generator counterpart (Nee et al., 2000).  In PM synchronous machine, the field winding is replaced by magnets. There is no need for external supply for field excitation. Hence, the magnetic field is achieved by using natural magnets but not electromagnets. In this case, the flux remains the same. The efficiency of the machine is improved as copper loss is reduced due to the use of magnets. However, in most cases, aging of the magnets at elevated temperature may totally demagnetize the magnets. Such problem can also happen under high armature reaction on load, or short circuit fault.

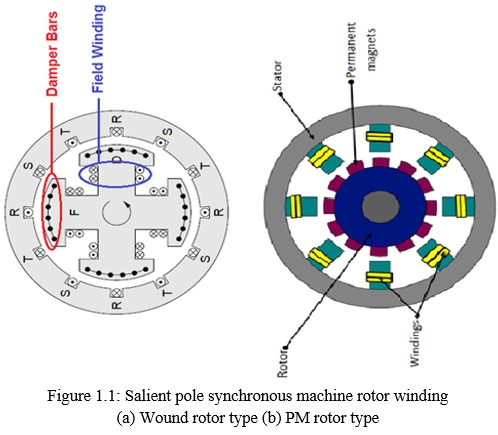
(a) Wound rotor type (b) PM rotor type

A special type of synchronous generator is the synchronous reluctance generator. This generator developed to overcome the weakness of induction generator, which includes frequency change as a result of change in load over time. Hence, the generator combines the features of synchronous generator and that of induction generator because it is self-stating. Like other self-excited AC generators such as the PMSGs, self-excited induction generators. Owning to the recent trend for distributed generation and the need for alternative and renewable energy sources, self-excited synchronous reluctance generators have attracted more attention for wind, tidal and hydro power generation applications.

Compared to conventional synchronous generators, they have the advantages of brushless features, robustness, low cost with no need for a DC excitation. Compared with self-excited induction generator, self-excited synchronous reluctance generator not only has the advantages of simplicity and ruggedness, but can also give high efficiency over a wide range of operation (Chan, 2005). Moreover, its output frequency is determined only by the prime mover speed, rather than by both load and the prime mover speed as in an induction generator, so it can be easily integrated with a power electronic converter to control the output (Nonaka and Kawaguchi, 1996). For the synchronous reluctance generator, the operating temperature is limited only by winding insulation. So with appropriate design consideration, the power/weight ratio can be improved and comparable to permanent magnet synchronous generator. Most fundamental operations of induction motor in the industry constitute about 95% of all rotating electrical machines. The commonest induction motor is the single-phase induction where there is power supply on only one side of the air-gap, while electric currents flow on the other side as a result of induced emf from main supply source. Therefore, the problem of poor output frequency in most machine operations has become a major robust engineering concern, especially in industrial operations where more cost of tariff for energy consumption are incurred most times. Knowing the arrangement of the conventional induction motors problems and the ways to reduce the known problem/disadvantages of not having sufficient magnetic flux density in the stator (Lipo, 1991b).  Although previous studies (Ben-Hail & Rabinovici, 2021; Binns and Kurdali, 1979) have been carried out whereby it was realized that series connected capacitor with generator load can improve the machine power factor. But this research study considered a shunt connected capacitor with the generator load as a means of addressing the need to improve output frequency of this machine which is independent of connected load provided the motor speed is kept constant. This then brings about sustaining self-excitation when appropriate value of a capacitor bank is properly connected across stationary terminals.

II. MATERIALS AND METHODS

The dynamic and transient models of the synchronous reluctance generator as well as the equivalent circuit were developed from a set of differential equations using classical algebra based on Park’s model. The steady state equations were derived by linearizing the dynamic equations. It is very important to introduce a realistic mathematical circuit model. The mathematical model of the stator and rotor voltage equation for synchronous reluctance generator in the arbitrary rotating frame is expressed as:

III. RESULTS AND DISCUSSIONS

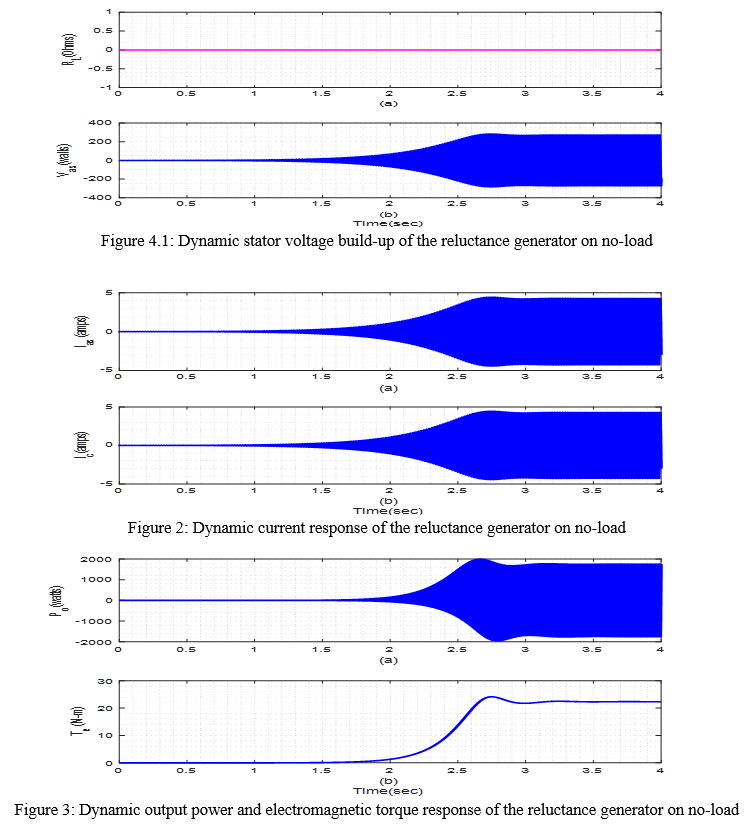
The per phase voltage buildup of the three Synchronous reluctance generator is illustrated in Figure 1. At this point, the generator is operated at almost no-load condition (balance three-phase) with start-connected capacitor bank, with excitation capacitor value of 50µF each and unity load power factor. The voltage then builds-up from 1.5 seconds maintaining a steady-state value up to 3 seconds and above, at peak voltage value of 250 volts. The current profile is illustrated in Figure 2, for the stator current and capacitor current with the peak currents of about 4.5 amps. This means a large portion of current goes to the capacitor. The output power and electromagnetic torque is shown in Figure 3, with the output power given as about 1.7kW and the torque given as about 25N-m.

A. Voltage Profile of Synchronous Reluctance Generator on Ramp Load

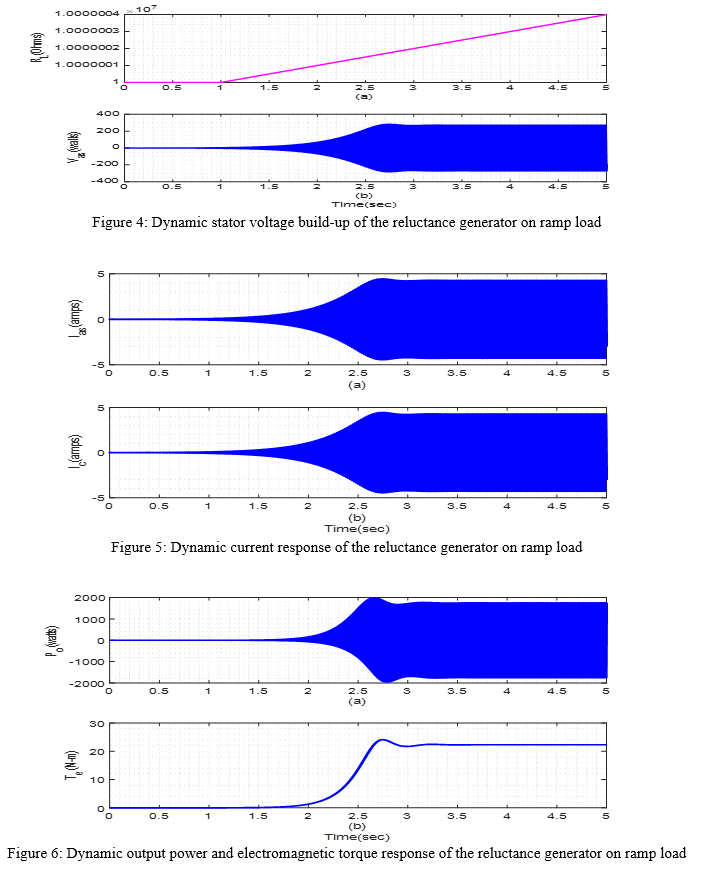
The simulation result in this section presents the voltage built up for existing synchronous reluctance generator on ramp loading operation. This is shown in Figure 4 through Figure 6. The voltage build-up started from 3.0 seconds and lasted to 5.0 seconds, maintaining a steady state voltage of about 230 volts. The current profiles for the stator current and capacitor current is illustrated in Figure 5 while the output power and electromagnetic torque is shown in Figure 6 where the output power is given as about 1800 watts and the electromagnetic torque given as about 24N-m.

B. Voltage Profile Of Synchronous Reluctance Generator On Constant Load

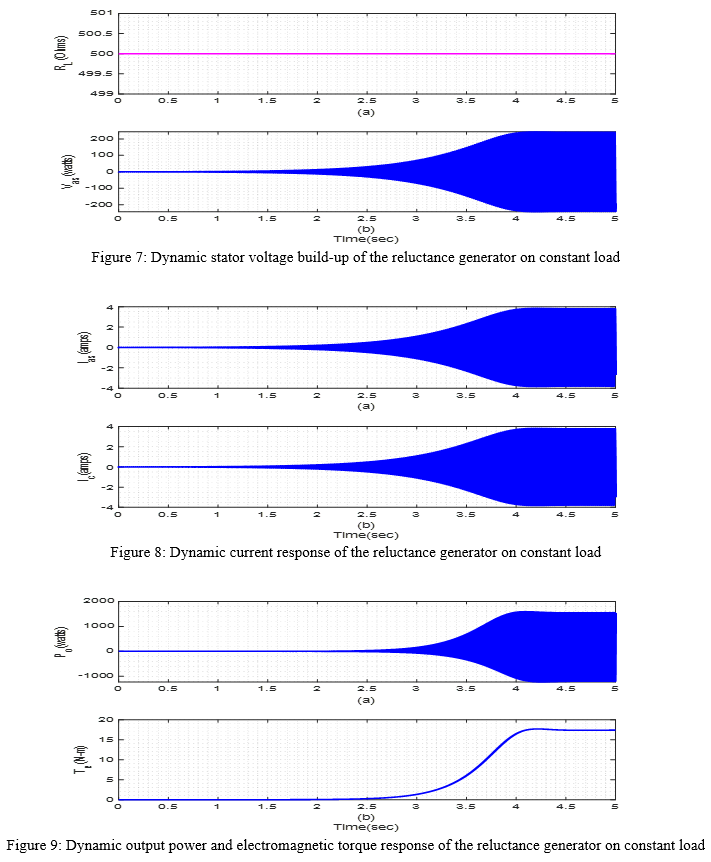
The performance of the synchronous reluctance generator on constant load is illustrated in Figure 7 through Figure 9. The voltage build-up is shown in Figure 7. The constant load is 500?. Here the voltage reduced as more load was applied. The voltage reduced to 220volts. This means the higher the inductive load the lower the terminal voltage of the generator. Reducing the load therefor increases the terminal voltage. This same thing applies to the stator current and capacitor current, which are below 4amps as shown in Figure 8. The output power as well as the electromagnetic torque shown in Figure 9, where the output power reduced to 1600watts and the torque reduced to 17N-m.

C. Voltage Profile of Synchronous Reluctance Generator on Varying Load

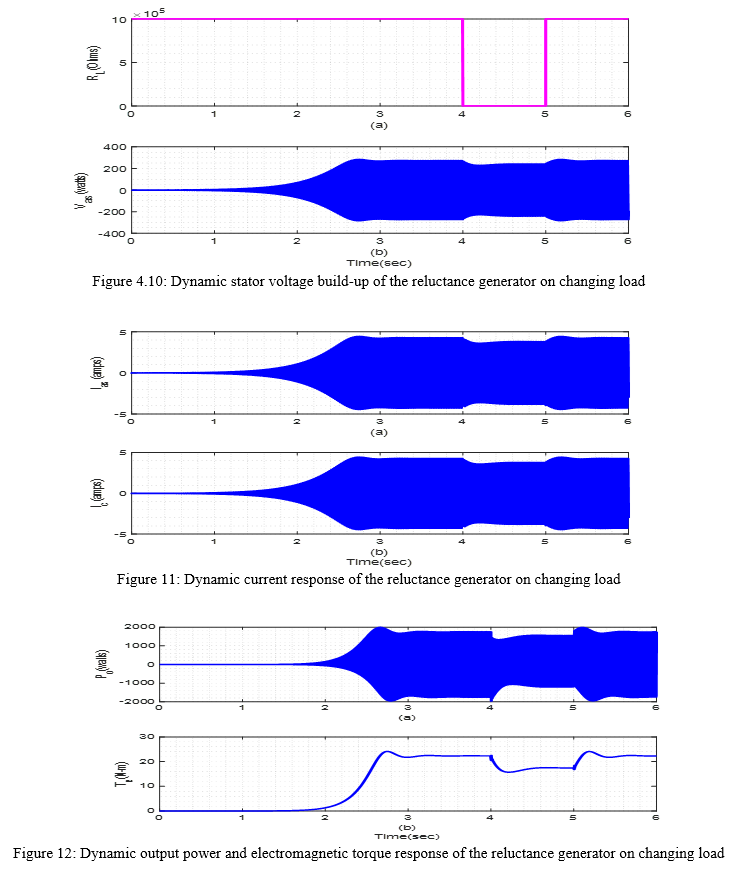
The load of the generator was also made to vary from no-load to full-load and then back to no-load.  A different result was obtained. The profile of the voltage is shown in Figure 10. At no-load, the voltage builds-up to about 250volts. When the load was made full, the voltage reduced to about 220volts. That was from 4.0 seconds to 5.0 seconds, before load was reduced again. The current profile for the stator and capacitor is illustrated in Figure 11. There was also an increase and reduction in current when the load was made low and high. This is also seen for the output power and electromagnetic torque illustrated in Figure 12.

Conclusion

The dynamic and steady state analysis of a three-phase synchronous reluctance generator feeding an R-L load have been carried out in this work. The analysis as based on the d-q model techniques. Equations and equivalent circuits based on these techniques were developed and used to examine the performance of the generator on different loading condition including ramping and transient loss of load condition. The steady state equations and the steady state equivalent circuits were developed from the dynamic equations by setting all time depended variables to zero. The study was successful using MATLAB/Simulink where relevant machine quantities such as output power and terminal voltage were measured. Real machine parameters were used for the creation of the codes. The graph results of the various methods were as well analyzed. It was observed that the generator output power as well as the terminal voltage drops when the load increases. Again, increasing the excitation capacitance increases the overall generator performance.

References

[1] Adkins B. (1957). The General Theory of Electrical Machines, London: Chapman & Hall Ltd. [2] Chan T. F. (2005). Steady-state analysis of a three-phase self-excited reluctance generator, IEEE Trans on Energy Conversion, 2(1), 223-230. [3] Chuong T. T. (2015). The Impact of Wind Power Plant with Doubly Fed Induction Generator on the Power Systems, International Journal of Science and Technology Education Research 4(1), 1 - 10, Available online at: http://www.academicjournals.org/IJSTER. [4] Fitzgerald E. (1990). Electric Machinery, 5th Ed., McGraw-Hill. [5] Hail, N. & Rabinovici R. (2021). Three-phase autonomous reluctance generator: IEE Proc. Elect. Apple, 148(5), 438-442. [6] Binns, K. J. & Kurdali, A. (1979). Permanent magnet a.c generators, Proc. IEE, 127(7). [7] Lipo T. A. (1991b). Novel reluctance concepts for variable speed drives, Mediterranean Electrotechnical Conference, MELECON, 34–43. [8] Miller T. J. E. (1986). Brushless permanent-magnet and reluctance motor drives, New York: Oxford University Press. [9] Nonaka, S. & Kawaguchi T. (1996). A new variable-speed AC generator system using a brushless self-excited-type synchronous machine, IEEE Trans. on Industry Applications, 28(2), 490–496. [10] Okoro O. I., Agu, M. U. & Chinkuni E. (2006). Basic principles and Functions of Electrical machine, A Pacific Journal of Science and Technology, 7(1). [11] Peter F. Ryff, David P. & Joseph A. K. (1989). Electrical Machines and Transformer, principle and Applications, Prentice Hall, Inc.

Copyright

Copyright © 2022 C. G. Enemor, D. C. Idoniboyeobu, S. L. Braide. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.