Numerical Simulation of Reinforced Concrete beam Under Flexure Using Finite Element Method

Abstract

Understanding the response of concrete structural components such as beams, columns, walls during loading is indispensable for the development of safe and efficient structures. The present report deals with the non-linear static analysis of a Reinforced Concrete (RC) beam, having dimensions 4000mmX400mmX 250mm, with 4 nos. of 16mm diameter bar as main reinforcements, 8mm diameter at 200mm c/c as shear reinforcement, with two faces of the beam as fixed modeled and analyzed when subjected to two point loads at one- third span from each fixed support using the Finite Element Analysis software Ansys. The behavior of the analyzed beam has been observed in terms of flexural behavior, load-deflection responses, and crack pattern for various loading conditions until failure load.

Introduction

I. INTRODUCTION

A. Motivation: Why Finite element Analysis?

The safety and serviceability assessment of reinforced concrete structures necessitate the development of accurate and reliable methods and models for their analysis. There are a number of approaches for the study of the behavior of concrete structures, viz., experimental, numerical, theoretical, etc. Experimental based testing on the flexural behaviour of RC beam has been widely used as a means to analyze individual elements and the effects of concrete strength under loading. While this is a method which gives an actual and exact behaviour, it is extremely time consuming and expensive. Finite Element Analysis (FEA) is a numerical method used for the evaluation of structures, providing an accurate prediction of the component's response subjected to various structural loads. The use of FEA has been the preferred method to study the behaviour of concrete as it is much faster than the experimental method and is cost-effective. Finite element analysis method divides the element into smaller parts and analyses the element under given loading conditions and hence evaluates the response of the material. The response of the element is represented in terms of finite number of degrees of freedom as the value of unknown functions in set of nodal points.

When the nature of the exact solution of an element is unknown, a simple function is chosen to represent it; this function is known as the interpolation model. The interpolation model is generally a polynomial, due to the ease with which it can be programmed and operated upon by calculus. However, such an interpolation model must satisfy certain convergence conditions in order that the approximate solution so produced, converges to the exact solution on infinitely increasing the number of elements.

In the case of a 2 dimensional beam element in the xy plane, the interpolation model that satisfies the convergence conditions is: q = a0 + a1x +a2x 2 +a3x 3 (1.4) wherea0, a1, a2and a3 are constants determined by boundary conditions of the element.

The stiffness matrix of this beam is

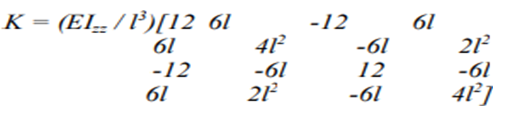
where Izz is the area moment of inertia of the cross section about the z axis, E is the modulus of elasticity of the material of the element, A is the area of cross section of the element and l is the length of the element.

The element stiffness matrix thus compiled can now be used to calculate the linear and angular deformation at each node using the following relation: [P] = [K] [Q] where[P] is the load matrix indicating the force or moment applied on particular degrees of freedom of particular nodes and [Q] is the deformation matrix. In this case, the load matrix is known, the stiffness matrix is compiled using the given data and the deformation matrix is the unknown. Hence, rearranging the equation we can separate the    known quantities from the unknown ones as follows: [Q] = [K]^-1  [P].

Most of the problems are non-linear in nature. Non-linear analysis is a method that simulates the exact behaviour of the material in inelastic range and to identify the potential of high load carrying capacity of the components through redistribution and shear strength. Hence the non-linear analysis is an effective tool to obtain the exact solution.

II. DESCRIPTION OF THE BEAM MODEL

Experimental analysis is widely carried out to study individual component members under two point load conditions at one third of span. This method provides the actual behavior of the structure, but it is time consuming and expensive. With the invention of sophisticated numerical tools for analysis like the finite element method (FEM), it has become possible to model the complex behavior of reinforced concrete beams using Finite Element modeling software like Ansys, student version 2021 which has been used in the present case.

Dimensions of the RC beam considered are 4000mmX400mmX250mm. The beam is fixed at both ends. Two point loads are applied at one- thirds of the span. The details of the beam are shown below:

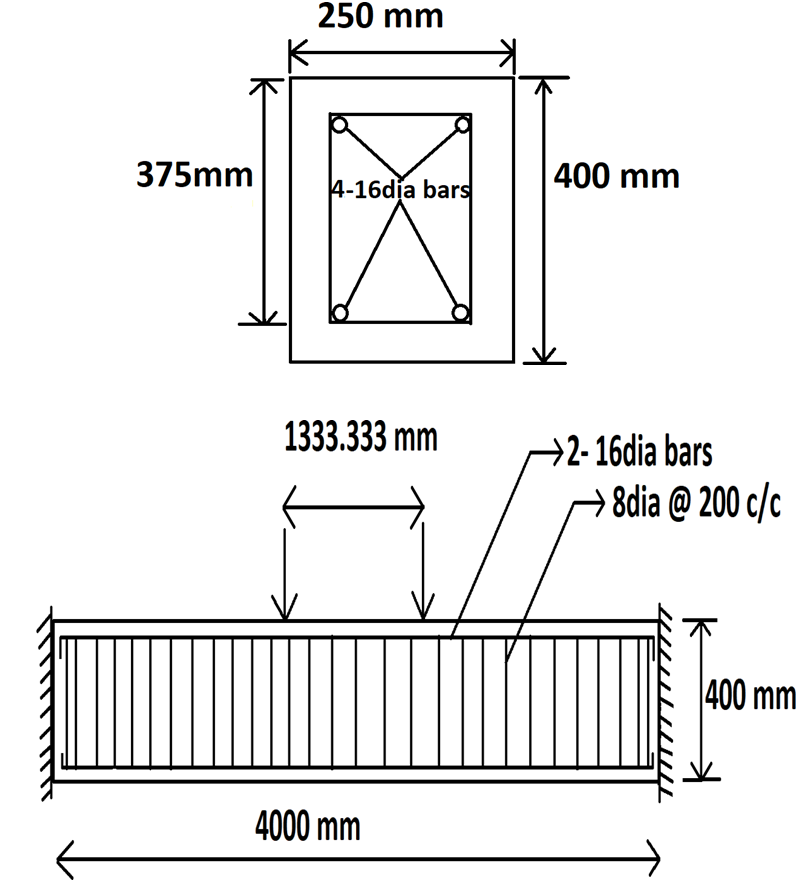
III. MATERIAL PROPERTIES.

1. Concrete Properties: Concrete is a quasi-brittle material and has different behavior in compression and tension. Modeling an    element for the behavior of concrete is a challenging task. In this study, concrete of M30 grade is considered. Modulus of elasticity Ec=5000(fck)^½ as per IS 456:2000 codal provision is calculated and taken as 27386MPa. The shear transfer coefficient for open crack and closed crack are taken as 0.3 and 1 respectively. Uniaxial tensile cracking stress obtained using ft = 0.7 (fck)^½ as per IS 456: 2000 is found out to be 3.834MPa.

Concrete material properties are shown in Table-1.

2. Steel Reinforcement: Steel reinforcement in RC beam is of grade Fe415. The steel for the finite element models has been assumed to be an elastic- perfectly plastic material and identical in tension and compression. Poisson’s ratio of 0.3 has been used for the steel reinforcement in this study. Elastic modulus equal to 200,000 MPa and Poisson’s ratio of 0.3 has been used for all the reinforcing bars. The reinforcing steel was assumed to have bilinear isotropic properties with yield stress of 415 N/mm2 and tangent modulus 20 N/mm2.

IV. ELEMENTS USED FOR MODELING THE BEAM

1. Solid 65: For the finite element modeling of the beam in Ansys, SOLID 65 is used to model the concrete which has three degrees of freedom at each node. The special feature in SOLID65 is cracking in three orthogonal directions, plastic deformation and crushing. The Solid65 element requires linear isotropic and multi-linear isotropic material properties to properly model concrete. The multi-linear isotropic material uses the Von-Misses failure criterion to define the failure of the concrete. Simplified stress strain relationship for concrete  in compression is obtained and is shown below:

2. LINK 180: For modeling steel reinforcement, Link180 spar element with three degrees of freedom at each node is used. LINK180 is a 3D bar that is useful in a variety of engineering applications. The element can be used to model trusses, sagging cables, links, springs, and so on. The element is a uniaxial tension-compression element with three degrees of freedom at each node translations in the nodal x, y, and z directions. As it is a pin jointed element, no bending of the element is considered.

Table2: Material property of Beam model:

V. MESHING AND BOUNDARY CONDITIONS

The beam was meshed such that it consisted of square elements of size 50mm. The necessary mesh attributes were set before the    volume was meshed. Merging of nodes and key points were carried out to avoid errors due to multiple nodes at the same location.

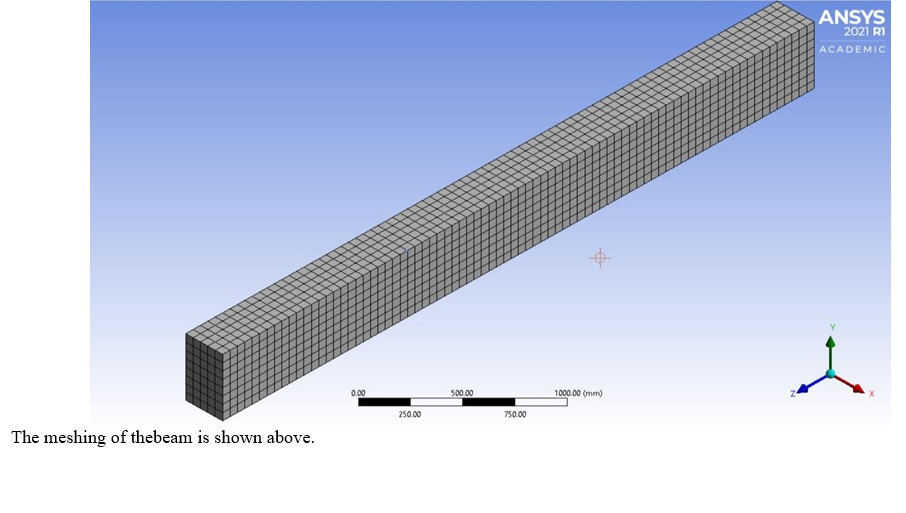
A. Modeling of the RC BEAM

The ANSYS version 2021R1 has been used to model the beam and the analysis part also has been conducted in ANSYS. The concrete beam has been modeled as volume, whereas the reinforcements and stirrups are modeled as line bodies. The model is 4000 mm long with a cross section of 400 mm X 250mm. The finite element model of the beam is shown below

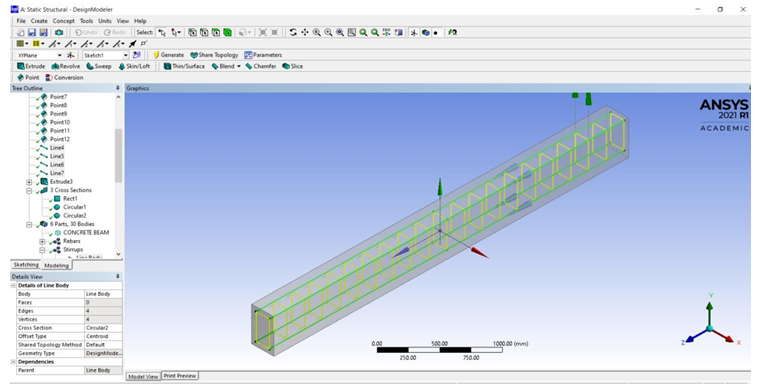
B. Loading and Boundary Conditions

Boundary conditions are required to constraint the model to get a unique solution. The supports were modeled as fixed supports at both end-faces. Self–weight of the concrete beam was taken into account by providing the value of acceleration due to gravity (9.81m/s2) along negative-Y axis. The external loads were applied as concentrated forces at equal one- third distance of the beam. The external loads were applied as concentrated forces acting at one third span.

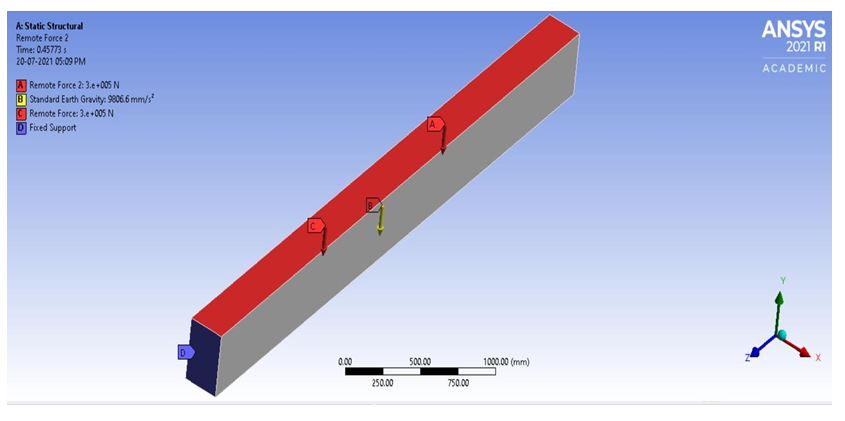
C. Analysis

For the analysis of the model, the static analysis type was utilized. The analysis was carried out for ‘Small displacement static conditions. In order to predict the nonlinear behavior, the total load is to be divided into series of load increments as required by Newton Raphson method. The load increment can be applied over several load steps. The number of load steps required for the study is given and the time for each load step is mentioned. During the initiation of concrete crack, the steel yielding stage and at the ultimate stage where large numbers of cracks occurs, the loads are applied gradually with smaller load increments. Failure of the model is identified where the solution fails to converge even with very low load increment.

VI.  RESULTS

The analysis was seen to terminate at the sub step corresponding to 330.35kN due to non- convergence of solution. Therefore, it was concluded that failure of the beam had taken place and 303 kN was taken as the failure load for the model. The first crack in the FE model was a flexural crack(vertical) near the corner edges of the beam , formed at 34.953kN. The deflections and stresses in the beam were seen to increase with loading. Cracking also progressed consequentially and was observed to increase in the constant moment region before it spread out towards the supports in the form of diagonal cracks. The beam was seen to fail due to excessive cracking of concrete in the tension side. Therefore, failure of the beam was attributed to flexural failure and yielding of the steel reinforcement. The ultimate mid-span deflection of the model was 47.951 mm at 330.35kN.

A. Load-Deflection Curve

Load-Deflection Curve is linear with a sharp slope up to 34.953 KN. At this load first cracking occur. The graph changes its nature after first cracking i.e. its slope is changed continuously. This is due to change in crack depth with the load increment. The location of initiation of the diagonal tension cracking of concrete in curves is in between the 1st cracking loads and steel yielding loads This crack is observed from concrete cracks and crushing plots which is within    250-300 KN.

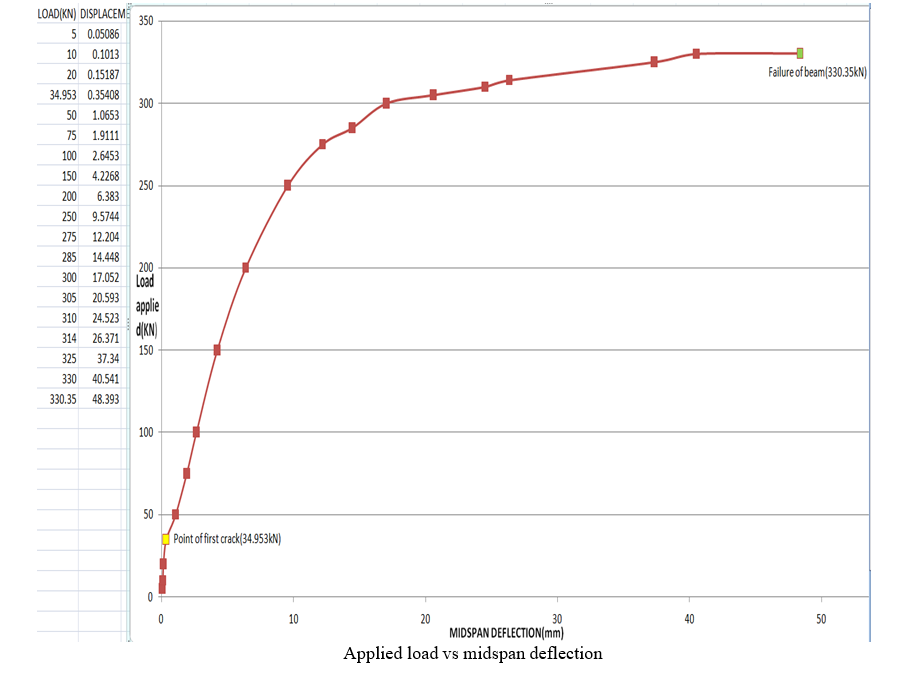
B. Effect of MESH Density

The accuracy and the convergence of the results  primarily depend on the mesh density. An optimum mesh density is arrived by conducting few numbers of trial analyses by varying the mesh density. For the study on mesh density, four trial analyses are carried out using 50mm , 75mm, 100mm and 150mm Solid65 concrete elements. A plot of load versus midspan deflection shows that the behaviour remains almost same up to steel yielding stage. After the yielding of steel, there is a small variation in the load versus deflection behaviour. It is also observed that for model with 150 mm size elements , the analysis terminated at 323.7 kN due to nonconvergence problems. The plot of number of elements versus midspan deflection at ultimate load,cwhich shows little variation of midspan deflection with respect to size of elements from 50 to 200 mm. Hence as a preliminary step a few numbers of trial analyses are carried out to decide the optimum mesh density.

The numerical crack and stress distributions at ultimate load are illustrated in the following figures

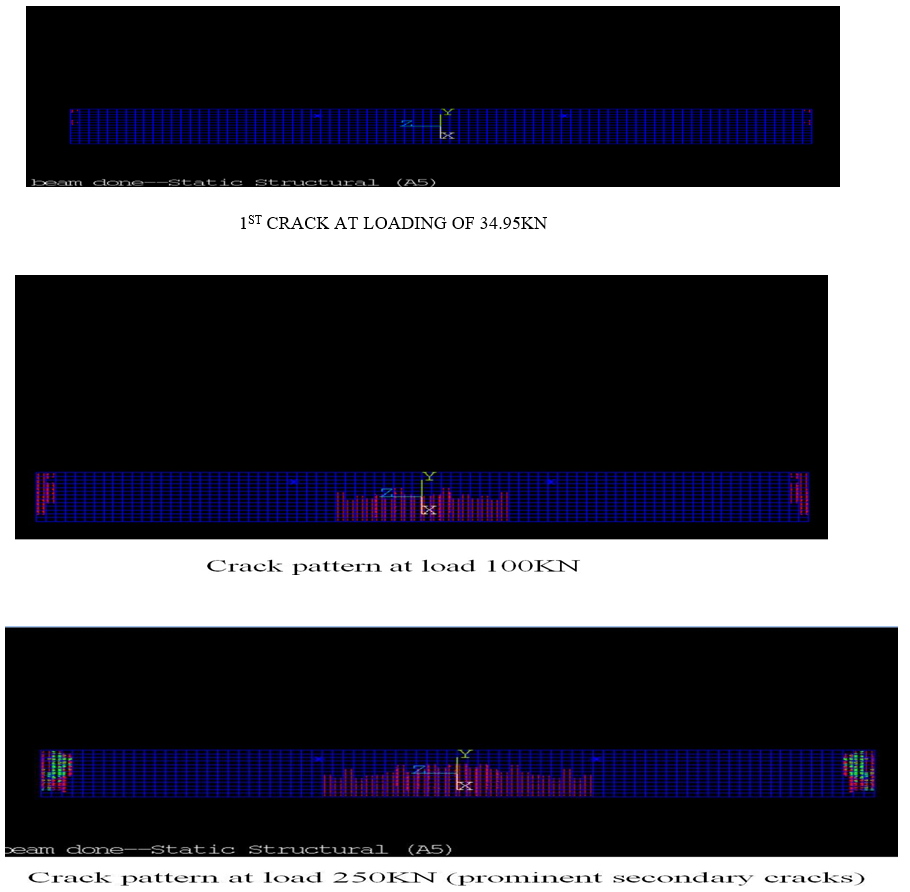
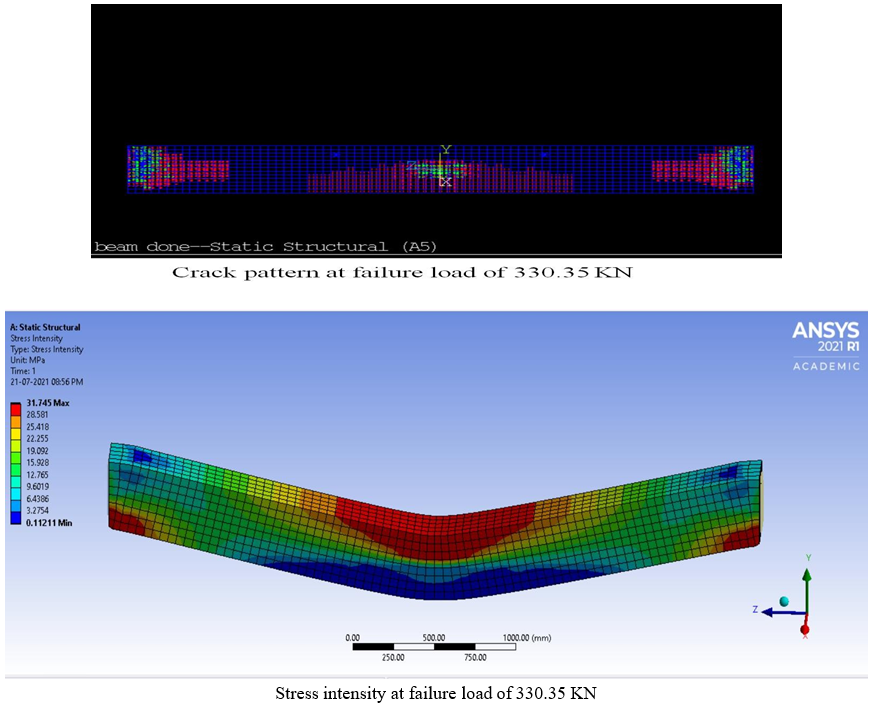
C. Comparison with Theoretical Values

The theoretical value of mid-span deflection of a fixed beam due to point-loads at one-third lengths of the span, was found out to be 5P(L^3)/648EI. Along with it, the self weight of the beam is also considered as a udl of W(inN/mm).

TOTAL DEFLECTION OF THE BEAM =

5P(L^3)/648EI + W(L^4)/384EI where E = 27386 Mpa, I= 15.46 X 10^8 (mm^4)

W= 2.45 N/mm.

Deflection due to self-weight was found out to be 0.0386mm.

Thus, Total deflection= 5P(L^3)/648EI + 0.0386 mm.

The theoretical value of the cracking moment was found out to be 29.8975 X 10^8 mm. Since it was observed that first cracks appear in the beam immediately adjacent to the fixed supports, cracking moment has been  equated with the support moment to get the value of load at which first crack occurs.

The theoretical value of the load at first crack was found out to be 33.634 KN. The reason for a slight decrease in the value of load at first crack ( 34.953 KN on analysis with Ansys while 33.634 KN being the theoretical value) is to be attributed to the 8mm diameter stirrups used which controls the development of crack and its growth. Before initiation of cracking, the deflection values obtained from Ansys is lesser than theoretical deflections at similar loads. A possible reason for this could be due to the   increase of flexural rigidity (EI) owing to the addition of rebars both in compression and tension zone. After cracking starts at 34.953 Kn, the deflection increases non-linearly with crack- growth and the theoretical value of deflection for an uncracked section will then give erroneous values of deflection and thus are not in accordance with the values obtained from finite element software.

Conclusion

In the present study, the response of reinforced concrete beam is analyzed using finite element method. The parameters used in this study are magnitude of load. The load-deflection response, stress intensity, crack patterns have been observed. After compiling and analyzing the model, following conclusions can be drawn: 1) Reinforced concrete beam can be modeled and analyzed using ANSYS 2021 R1 software and obtain accurate results. 2) The total load is to be divided into a number of suitable load steps (load increments) by conducting a few trial analyses until a smooth load versus deflection curve is obtained. 3) From the analysis of the beam under various loads it was found that by increasing the load, stress intensity is increased gradually and consequently deflection also increased. 4) The tension and shear reinforcements are to be precisely incorporated using discrete modelling technique in order to get more accurate behaviour.

References

[1] P. Fanning, “Nonlinear Models of Reinforced and Post-tensioned Concrete Beams”, Electronic Journal of Structural Engineering, Feb February 2001. [2] Diyyala Naga Moulika, Reshma Vasireddy, P. Polu Raju, “MODELLING AND ANALYSIS OF REINFORCED CONCRETE BEAM UNDER FLEXURE USING ANSYS”, International Journal Of Civil Engineering and Technology, March 2017. [3] Anthony J. Wolanski, B.S, “Flexural Behavior of Reinforced and Prestressed Concrete Beams Using Finite Element Analysis”, A Thesis submitted to the Faculty of the Graduate School, Marquette University, May, 2004 [4] Vasudevan. G, Kothandaraman.S, “Parametric study on Nonlinear Finite Element Analysis on flexuralbehaviour of RC beams using ANSYS”, International Journal of Civil and Structural Engineering, Volume 2 Issue 1 2011.

Copyright

Copyright © 2022 Kingshuk Mukherjee. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.