Reliability Characteristics of Machining Systems and Some Queueing Theory Regarding the Machine Repair Problem

Abstract

The article delves into the elements of machine repairable systems that contribute to their dependability, as well as certain parts of queueing theory. The use of reliability theory, which is both a mathematical and physical discipline, has aided in our understanding of the laws that control the incidence of failures in machining systems. Life testing, structural reliability, machine maintenance concerns, and the replacement problem are all subfields of reliability research. When dealing with bottlenecks and delays in complicated machining systems, the idea of queueing is often a useful tool. People wait in lines or line ups in many real-world situations, including at traffic lights, phone assistance lines, petrol stations, airports, hospitals, via communication channels, in computer systems, etc. One important subset of queues is made up of queues with finite source populations. Some of the numerous domains that might profit from this class include production, power generation, manufacturing techniques, information and communication technology, and distribution hubs.

Introduction

I. INTRODUCTION

A. Reliability and its Characteristics of Machining Systems

Reliability theory, a combination of mathematics and physics, has been a huge help in deducing the laws that govern the occurrence of failures in machining systems. Life testing, structural dependability, machine maintenance challenges, and the replacement problem are just a few of the many subfields that fall under the broader umbrella of reliability.

Since it is inconceivable to conceive of technological operation without dependability, the reliability theory is crucial for foreseeing and developing industrial systems in a machining context. Reliability technology is used in many different industries, including defense, biomedicine, mining, electronics and electrical engineering, manufacturing and production systems, communication and computer systems, etc., and has the potential to solve virtually every problem that arises in these areas because of machinery. The term "reliability" is used to indicate the likelihood that an issue will not arise within a certain amount of time. The word "reliability" is used to describe the consistency with which a unit (or component) performs its intended function over a period of time and under certain environmental conditions. A unit may refer to either an individual part of the system or the whole system depending on the context. The reliability of a machining system is a major factor in gauging its overall performance. A component's dependability is contingent on several factors, most of which are, by definition, arbitrary. Valuing it is difficult since there is no dependable measurement equipment. This adds a great deal of complexity to the procedure. Any complex system's dependability is determined by various variables, such as the method of production, the materials used, and the conditions in which the equipment is operated.

The concept of Reliability emphasizes the following four factors:

1. Probability
2. The desired purpose
3. Time
4. The established work environment

If T is the remaining time before the unit fails, followed by the possibility that it will continue to be dependable.

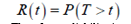
Therefore, reliability is conditional on a number of variables, such as the passage of time and the existence or absence of fluctuating environmental conditions. In all cases, the associated number will be non-negative and less than one, as befits a representation of a probability.i.e.

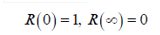
and R (t)  is a function which remains flat within these bounds.

B. Queueing Theory

In many commercial settings, machines tend to break down unexpectedly. With increasing numbers of people depending on them, computers have become an integral part of modern life, enhancing almost every facet of it. Thus, there is an urgent need to use state-of-the-art mathematical methods in order to establish a systematic strategy for investigating phenomena related to machining systems. The concept of queuing is often used as an effective instrument for addressing bottleneck and delay concerns in intricate machining systems. Virtually every aspect of modern life necessitates the usage of line-ups, from traffic lights and phone lines to petrol stations, airports, hospitals, communication channels, computer systems, etc. The queue with a finite source population is a particularly useful class of queues. The supply of power, the management of industrial processes, the construction of computer networks, and the management of distribution networks all fall under this category. The "Finite Source Queuing Model," also known as the "Machine Repair Model" and the "Machine Interference Model," has several practical uses. Various machine shops employ these applications.

It is becoming more difficult for system designers and engineers to keep up with the increasing complexity of machining systems. We assume that any manufacturer that uses a machining system strives to increase output (in terms of both quantity and quality) while simultaneously minimizing production expenses.

Inefficient machining components might sometimes degrade the overall system performance. A repair facility is often included into the system to avoid service interruption and lost productivity. Their goal is to repair faulty systems. Evaluating the success of approaches to the difficulties of real-world machining in and around industrial regions requires the use of mathematical tools and models based on the theory of queuing. Various mathematical methods and models might be used in this inquiry. Businesses, by accepting and executing fresh ideas, and universities, by solving and addressing unique, tough challenges. This has the potential to help both academic institutions and industry by giving universities the opportunity to confront and generate novel, difficult problem statements.

The machine interference models have potential applications in the actual world, particularly in the manufacturing and industrial settings. An FMS, or Flexible Manufacturing System, may be used to facilitate the automation of production over a broad variety of scales, from medium to tiny to even vast. The Machine Repair Problem (MRP) has many applications, but one of the most significant is in the realm of computing. The reliability and accuracy of a computer system depend on both its hardware and its software. Several computers may operate together in a large network.

It's not only the manufacturing sector that may benefit from manufacturing resource planning (MRP).

This dissertation makes an attempt at simulating a real-world industrial setting. We've also done our best to provide some fresh methods for servicing, fixing, and eventually replacing the machining system, as well as some broad, overarching advice for doing so. By assisting with repair facilities and giving access to replacement parts, this goal has been met. Fixing any broken components quickly is essential for keeping the system running as intended. For this reason, preventative maintenance must be included into every machining process. If there are many people on the waiting list, it might be a while before everyone gets seen. As a result, clients may have to wait in lengthy queues to be assisted. However, it is very difficult to anticipate when and how customers will come in and how long it would take to service them. These decisions are not always foreseeable. Increasing the capacity of the service facility to deal with these problems is a costly endeavor. Customers would have to wait in line for longer, but the service would be cheaper if there were fewer service stations. The longer we wait, the more likely it is that society as a whole will lose money due to fewer people buying and producing goods. Consequently, the major objective is to achieve a balance between the cost of delivering the service and the cost of waiting for it to be given. Understanding how long customers typically have to wait, how many customers are typically in the system at any given time, and how to optimize our service needs to incur the lowest possible overall cost in the least amount of time is made possible by the concept of queues. In addition, it considers the sum of all servers, clients, and end users. The major motivation for the creation of queueing theory was the need to reduce client wait times for service.

1. QUEUEING Theory Regarding The Machine Repair Problem

Years of experience have shown that queueing models perform better in practice than deterministic ones. This information has just recently been made readily available.

In nontrivial fields, such as applied industrial research and the more broad disciplines of common sciences like statistics and operations research, queuing models are most often used. In-depth analysis of numerous models of congested service delivery is the focus of queueing theory, a subfield of applied probability theory. This is a nice illustration of the usefulness of probabilistic models in practice. To get the service they have requested, customers join a queuing system, wait in line (if necessary), and then exit (if the service was provided quickly). Queueing theory has been around for quite some time, and in that time it has sought to give answers for a broad variety of fundamental concerns, such as the average response time of systems, the average time required repairing a system, the average time spent waiting in a line, and so on. All of the results are contingent on treating the times involved as random variables, including service time, inter-arrival time, etc.

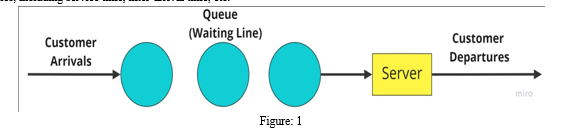
Source: Created by author

Queueing theory is made up of these primary parts:

a. What customers or users do after logging in

b. A breakdown of how the queue's members will be attended to.

c. The service's utilization steps, and eventually the student's departure

• The expected number of customers who will arrive during the service's availability timeframe.
• The length of the queue is relative to the number of individuals waiting at any one moment.
• Anyone or everything that needs a service is a prospective customer. This includes people, items, raw materials, and so on. Remember that the length of a line might be either finite or infinite.

The birth of queueing theory and its subsequent rise to prominence may be traced back to this moment. Erlang's straightforward explanation of statistical equilibrium included Poisson distribution-based answers to the issues of constant service times and arrivals. The financial sector, booking offices, automated equipment, telephone networks, railroads, elevators, the travel and transportation industry, and many more have all made use of the notion of queuing. For each of these applications, it is necessary to design, develop, and implement service facilities that can adapt to unpredictable fluctuations in demand, all while maximizing efficiency and minimizing the time wasted waiting in line. The development of queueing theory had its greatest success in the early 1950s.

2. Application Areas for the Theory of Queuing

There was a quantum leap in queueing theory made by mathematicians of this time. They also established queueing theory as a fertile mathematical ground for exploring and expanding theoretical applications, empirical discoveries, and statistical approaches. One needs a firm knowledge of probability and statistics to adequately appreciate queueing theory.

Since the inception of the very first telephone networks, queueing theory has provided the foundational research essential to comprehending their inner workings and operations. Throughout the whole decade of the 1950s, discussions of these distinct systems were commonplace. Applied research, including areas like queueing theory, underwent a paradigm change after World War II ended. Parallel to the development of probability theory proper was the emergence of reliability theory. Parallel developments occurred in the mathematical literature on this topic of applied probability theory about the same time. Around the same time, a variation on queueing and dependability called the "machine repair model" was developed and has since found widespread use in contemporary statistical analysis. This concept is used often in current debates about statistics.

Simultaneously, it was realized that a queue-based approach gave a far more straightforward and rational means of comprehending and modeling the dependability of apparently complicated systems. The simultaneous emergence of these two findings (arrivals of breakdowns and repair services).

To get a better grasp of the aforementioned domains of application for applied probability theory, the same statistical concepts, techniques, and procedures may be used.

The 1960s saw significant advancements in data transmission technology, which allowed researchers to begin investigating the possibility of modeling computer systems. This allowed for the study of queues, which later became typified by complex service systems, giving rise to the need to analyze and evaluate linked systems. Since the 1970s, there has been a tremendous increase in the range of industrial uses for this area. Since then, there has been a rise in the number of applications in industry.

There is no doubt that queueing network analysis is a fundamental part of the study of communications. Now that computers are so pervasive in large-scale communication systems, we may include newly obtained data on queuing networks into studies of their efficiency.

3. A Concept of Machine Repair Problem (MRP)

The random breakdown and systematic repair of components of machining systems have a substantial effect on the outputs and productivity of machining systems. This is due to the fact that it is the machining systems' components that really perform the necessary functions. Constant and trouble-free operation of the machining system is dependent on effective maintenance and repair procedures. While designing and analyzing the machine, it is essential to predict how a breakdown may affect output in the event of continuous production. For instance, issues with machine interference and machine maintenance are both examples of problems that may be modelled as populations from limited sources that can be sampled. As a result of a lack of upkeep resources or an obstruction in the system's route, congestion may arise in such setups. A main and secondary repair facility might be included into the system to prevent this from happening.

With the standbys support option, for an additional fee, the system may keep running normally by automatically replacing a broken computer with a standby. In order to keep production going smoothly, we quickly locate and swap out any faulty components of the machining system with replacements. However, component shifting may go wrong for a variety of reasons and in a wide range of contexts. So that damaged equipment may be repaired swiftly and the company can keep working, a machine repair center must be built. Factors like machine age, repair wait times, the quantity of malfunctioning machines, and the like may all have an impact on machining systems. With a large number of available specialists, malfunctioning machinery will be given first priority. Until a technician is available, those machines will have to wait. As a result, there is interference loss and output is diminished.

a. Machine Repair Model

Using a finite source queueing model to address machine maintenance issues is a tried and tested method. In this scenario, the machines represent a prospective clientele, new machines replace malfunctioning ones, and maintenance technicians replace the servers. Let's say we have a problem mending PCs and we have M computers running the same OS and R technicians to fix them. The average amount of time it takes to repair a machine follows an exponential distribution with a mean of one, and the maximum amount of time it can run before breaking down follows a similar distribution with failure as the limit.

Let us presume to n P is the probability, under steady state circumstances, that n machines will fail. Below is a state transition diagram for a Continuous-Time Markov Chain (CTMC) model appropriate for predictive maintenance of equipment.

Repairing the malfunctioning components is urgently required to ensure the system's regular operation. For this reason, preventative maintenance must be included into every machining process. If there are a lot of individuals, it might take a while to evaluate everyone. This might lead to significant delays, lines, and service interruptions. However, it's difficult to anticipate when and how damaged devices will arrive, or how long it would take to repair them. The results of such assessments in nature are often unexpected. Increasing the capacity of the service facility to deal with these problems is a costly endeavor. While consolidating service sites into fewer hubs might save money, doing so would likely lead to appreciably higher wait times. The end result will be an intolerable lag in service, costing customers precious time. Whatever the situation may be, the longer the delay, the higher the associated expenditures will be. Thus, the key objective is to find a happy medium between the service's cost and the amount of time required to get it. Using queueing theory, one may make a reasonably accurate prediction of the efficiency of the machining systems. In many machining procedures, success or failure is based on chance. These measures are often derived from random variables such as line length, busyness, and waiting time.

The following formulae may be used to calculate a variety of useful performance indicators:

Conclusion

Not only do defensive systems that depend on electronics, computers, and communication require a backup supply, but so do the majority of other types of systems. Using the right number of spares is one technique to get the most amount of system uptime for the least amount of money. Spare units and reneging together may be necessary in a variety of intricate situations involving machining systems in today\'s technological production processes in order to lower the expected cost function. An overwhelming number of factors may affect the dependability of any particular component; the great majority of these factors are inherently unpredictable. Considering the lack of a standard assessment for dependability, it is difficult to assign a monetary value to it. This adds a great deal of complexity to the procedure. The production method, the kind of materials used, and the operating conditions of the equipment all impact the degree of dependability that may be expected from the many components that make up any complex system. Queueing theory is a subfield of applied probability theory that examines in depth the dynamics of high-volume service settings. Users use the system to request a service, wait for that service to become available (if it isn\'t provided instantly), and then exit the system once it has been provided. Queueing theory has been around for quite some time, and in that time it has sought to give answers for a broad variety of fundamental concerns, such as the average response time of systems, the average time required to repair a system, the average time spent waiting in a line, and so on. All of the results are contingent on treating the times involved as random variables, including service time, inter-arrival time, etc. Thus, the key objective is to find a happy medium between the service\'s cost and the amount of time required to get it. Using queueing theory, one may make a reasonably accurate prediction of the efficiency of the machining systems.

References

[1] Abou-El-Ata, M. O., & Shawky, A. I. (1992). The single-server Markovian overflow queue with balking, reneging and an additional server for longer queues. Microelectronics Reliability, 32(10), 1389-1394. [2] Kalpakam, S., & Hameed, M. A. S. (1984). Availability and reliability of an n-unit warm standby redundant system. Journal of Mathematical and Physical Sciences, 18, 41-50. [3] Gupta, S. M. (1999). N-policy queueing system with finite source and warm spares. Opsearch, 36(3), 189-217. [4] Yadin, M., & Naor, P. (1963). Queueing systems with a removable service station. Journal of the Operational Research Society, 14(4), 393-405. [5] Ke, J. C., & Wang, K. H. (1999). Cost analysis of the M/M/R machine repair problem with balking, reneging, and server breakdowns. Journal of the Operational Research Society, 50(3), 275-282. [6] Zhang, Y. L., Zuo, M. J., & Yam, R. C. (2000). Reliability analysis for a circular consecutive-2-out-of-n: F repairable system with priority in repair. Reliability Engineering & System Safety, 68(2), 113-120. [7] Yam, R. C., Zuo, M. J., & Zhang, Y. L. (2003). A method for evaluation of reliability indices for repairable circular consecutive-k-out-of-n: F systems. Reliability engineering & System safety, 79(1), 1-9. [8] Xiao, G., Li, Z., & Li, T. (2007). Dependability estimation for non-Markov consecutive-k-out-of-n: F repairable systems by fast simulation. Reliability Engineering & System Safety, 92(3), 293-299. [9] Ke, J. C., & Wang, K. H. (2007). Vacation policies for machine repair problem with two type spares. Applied Mathematical Modelling, 31(5), 880-894. [10] Cao, J. H., & Cheng, K. (1986). Introduction to reliability mathematics. Applied Mathematical Modelling, Beijing: Science Press. [11] Cao, J. (2011). Reliability Analysis of Gnedenko System with Multiple Vacations. In Advances in Computer Science, Intelligent System and Environment (pp. 283-287). Springer, Berlin, Heidelberg. [12] Chen, T., Wang, B., & Yin, D. (2017, December). Reliability analysis for single-unit system of warship equipment with one repairman having vacations based on phase-type distribution. In 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM) (pp. 1950-1954). IEEE. [13] Gupta, S. M. (1995). Interrelationship between controlling arrival and service in queueing systems. Computers & operations research, 22(10), 1005-1014. [14] Šeda, M., Ošmera, P., & Petrucha, J. (2011). Systems with Queueing and their Simulation. International Journal of Computer and Information Engineering, 5(1), 51-57. [15] El-Damcese, M. A., & Shama, M. S. (2013). Reliability and availability analysis of a standby repairable system with degradation facility. International Journal of Research and Reviews in Applied Sciences, 16(3), 501-507.

Copyright

Copyright © 2022 Sonam Bansal , Dr. Sharon Moses . This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.