SLIM: A Lightweight Block Cipher for Internet of Health Things.

Abstract

Increased protection of resource-constrained devices, such as radio frequency identification (RFID) systems, is in high demand these days. For high-resource desktop PCs, current encryption techniques are sufficient. Access control systems, transaction banking systems, and payment systems are all examples of high-security applications where RFID technology are used. The attacker tries to deceive RFIDs in order to gain illegal access to services without paying for them or to get around security measures by detecting a secret password. The most difficult problem with RFID systems is ensuring effective protection against such infringements. For RFID systems, lightweight cryptography can give security assurance. SLIM is a novel ultra-lightweight cryptography technique for RFID devices presented in this paper. Since block ciphers are the most commonly used cryptographic and provide highly strong protection for IoT devices, SLIM is a 32-bit block cipher based on the Feistel structure. The most difficult aspect of creating a lightweight block cipher is balancing performance, cost, and security. SLIM, like all symmetric block ciphers, encrypts and decrypts using the same key. The suggested method performs well in both hardware and software contexts, has a small implementation footprint, a reasonable cost/security ratio for RFID devices, and is energy-efficient. SLIM has shown high immunity to the most successful linear and differential cryptanalysis assaults, as well as a substantial margin of defense against them.

Introduction

I. INTRODUCTION

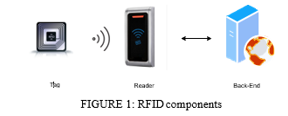
One of the world's most critical demands is the preservation of human existence. As a result, a real-time healthcare tracking system of patients' physical situation is one of the most significant criteria of hospital authorities. The Remote Patient Tracking System (RPMS) is a vital component of today's medical system, and it stores patient data in the cloud using a number of technologies, including the Internet of Things (IoT). In most smart medical systems, detection systems for physiological equipment send medical information from patients to a central healthcare server Control Room (CCR). In a critical situation, medical information will be sent to the doctor via the Global System for Mobile Communication (GSM) module. Individual healthcare information could be sent across an untrusted network or stored in an insecure cloud service, leaving confidential material vulnerable to cyber-attacks. Additionally, a major point must be recognized while broadcasting through source of energy IoHT devices. Conventional techniques cannot be used because of the nature of these devices. The majority of cryptographic algorithms in use today were designed and developed for the personal computing era. In today's world, tiny computing devices are quite ubiquitous; nonetheless, these source of energy devices constitute a potential threat. For software and hardware devices with restricted capacities, such as RFID systems, standard encryption techniques are not well adapted (seeFigure1). An RFID tag, a reader, and a back-end database are the three main components of an RFID system (server). In healthcare, RFID devices are used for patient identification and tracking, equipment and asset tracking, reducing blood and medicine administration errors, and other real-world applications. Apart from that, it has a wide range of real-world applications. Mobile payments, virtual passports, inventory tracking, and other examples are only a few. An RFID tag is connected to these products, which provides important information about products. An RFID tag, or transmitter, is a type of detector that consist of an integrated circuit (IC) and an antenna. The integrated circuit is used to store and compute information. The antenna establishes a connection between the transmitter and the sensor, allow people to interact. They may be attached to any object in the environment due to their inexpensive production costs. The three varieties of RFID tags based on their power supply are active tags, passive tags, and semi-passive tags. In healthcare, RFID devices are used for patient detection and quantification, equipment and asset monitoring, reducing blood and medicine administration errors, and other real-world applications. Aside from that, it offers a wide range of practical applications, such as contactless payments, electronic passports, product tracking, and so on. An RFID tag is connected to these products, which provides important product information.

A transceiver, commonly known as an RFID tag, is a type of identification device that consists of an integrated circuit (IC) and an antenna. The integrated circuit is used to store and compute information. The antenna establishes a connection between the transceiver and the reader, ability to connect. Because of their low production costs, they can be connected to any object in the surroundings. The three varieties of RFID tags based on their power supply are active tags, passive tags, and semi-passive tags. Passive RFID tags are significant in this article because they have very limited memory, power, and processing capability, making traditional security techniques impossible to implement.

This study offers a novel RFID restricted tag-friendly ultra-lightweight encryption method. The suggested approach is designed to keep RFID data and transmission safe. Easy RFID tag procedures will enable it to defend against with a number of risks, make it especially attractive to limited RFIDs. The most widely used cryptographic primitive is therefore block cipher, which provides highly strict security to IoHT devices but could be used for encryption, hashing, authentication, and random bit generation. A stream cipher can be generated by running a block cipher in counter mode, and the primitives of a block cipher are adaptable. Furthermore, the block cipher design is easier to grasp than the stream cipher architecture. The most difficult component of constructing lightweight block ciphers is dealing with trade-offs between performance, cost, and security. It is impossible to provide all three features to resource-constrained devices at the same time. The encryption in this work was carefully built with power and area limits in mind, and every effort was made to avoid any security compromises. The following properties apply to the cipher:

1. The Feistel structure is used to create SLIM, a symmetric block cipher. This means that the encryption and decryption keys are the same.
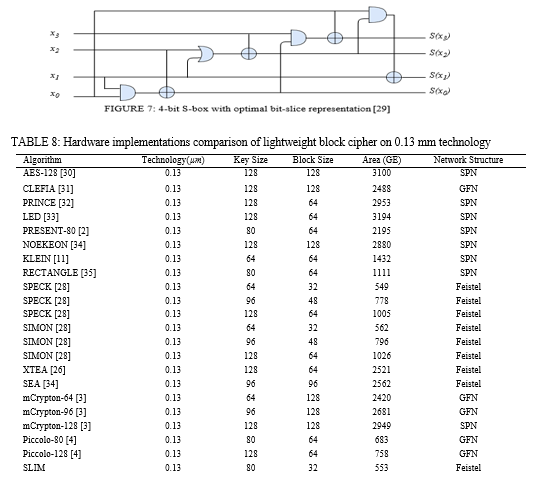
2. SLIM employs four 4 4 S-boxes as a non-linear encryption component that performs a non-linear operation on a 16-bit word.
3. Despite its ease of deployment and design, SLIM has a stiffness profile against the most successful detrimental cryptanalyses "linear and differential attacks."
4. The cipher is well-suited to the Internet of Things, and it can be easily deployed with resource-constrained devices such as RFID.

The following is the format of the paper: Section II provides an overview of the literature as well as contemporary lightweight cryptography approaches. The proposed algorithm architecture and its features are explained in Section III. discussed. Section IV discusses the SLIM algorithm's implementation considerations. In Section V, we'll talk about how to evaluate your performance. The findings of cryptanalysis against linear and differential cryptanalysis are shown in Section VI, demonstrating that the cipher provides enough protection against these two serious attacks. The paper came to a close with a conclusion and references.

II. RELATEDWORK

The amount of storage space available for the cryptographic feature in RFID devices is limited, and the amount of power that can be consumed is also limited. As a result, one of the most appropriate strategies for data confidentiality in these settings is the lightweight cryptographic algorithm. This section includes the most recent state of the art in lightweight primitives or algorithms aimed at overcoming the limitations of low-cost RFID. In that order, we'll look at block ciphers, stream ciphers, hash functions, and random number generators.RFID systems are subject to a wide range of threats. RFID technology is evolving at a rapid pace, and the risks are evolving as well [24]. Because of the nature of RFID tags, a variety of cryptographic algorithms must be used to address security and  privacy problems. Because the implementation of these systems would demand a lot of computational power, memory, and resources, modern encryption techniques built for high-end devices are not suited for RFID tags [25].

One of the most fundamental cryptographic primitives is block ciphers. The TEA block cipher [26] was one of the earliest lightweight block ciphers, appearing in 1997. Table 1 compares some of the most recent suggestions for lightweight block ciphers in terms of their specifications. Hardware implementation area (GE), speed (Kbps) at a frequency of 100 kHz, and CMOS technology are all used to compare ciphers (m). Two well-known lightweight block ciphers on the list are PRESENT [2] and CLEFIA [10].

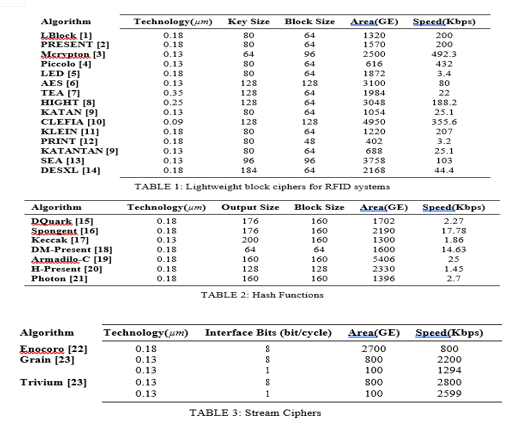
In suggestions for RFID security and privacy protocols, hash functions are widely employed. Table 2 examines the needs of various of the most recent lightweight hash algorithms. The algorithms presented in the table may have numerous variants in terms of block size, output size, or internal state size, but only one variant is mentioned as an example. There aren't as many as there are block ciphers. ideas for stream ciphers that aren't too heavy. Table 3 lists a number of current lightweight stream cipher proposals, including Grain v1 [23], Trivium [23], and Enocoro [22]. Grain v1 and Trivium, two hardware-oriented ciphers featured in the eStream project's portfolio, are the most popular. The Enocoro and Trivium algorithms, on the other hand, are the most used lightweight stream ciphers.

III. STRUCTURE OF THE PROPOSEDALGORITHM

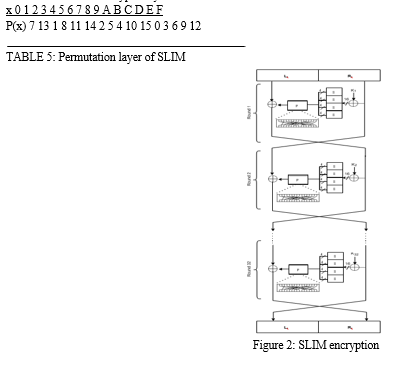
This section explains the structure of the suggested algorithm (SLIM). It's a type of symmetric encryption in which the same key is used for both encryption and decryption (encryption and decryption keys are identical). In both operations, the decryption sub-keys are applied in reverse order. Security and simplicity are two critical design challenges that are addressed in SLIM. By adopting the NIST guidelines report for key length, it establishes protection against the exhaustive search attack (key length 80). Confusion and diffusion are both achieved using SLIM. Confusion is solved using a tiny 4-bit S-box with high non-linearity features. The data is diffused using a combination of procedures in addition to the Feistel structure's nature.Simplicity is achieved, on the other hand, by the S-small box's size and the utilization of internal basic functions. The SLIM block cipher uses 32-bit plaintext and ciphertext blocks and is controlled by an 80-bit key. The main purpose of this algorithm's development is to have the smallest possible footprint for RFID applications. The cryptosystem was designed to be easy to implement in software and hardware. SLIM also consists of 32 rounds, each with 32 16-bit subkeys generated from an 80-bit key. The basic concept of the SLIM encryption method is shown in Figure 2. As seen in this diagram, the SLIM architecture is based on a Feistel structure. The input is divided into right and left sections, which run through multiple rounds, in addition to the created sub-keys (32-round). The key size might be 80 bits, and the input could be 32 bits.

A. Single Round processing

To discover more about SLIM's design, look at the real structure of a single round. The 32-bit input is divided into Li and Ri, which are equal sixteen-bit halves. Equations 1 and 2 show the full processing at each round, in which the XOR operation is used to change the right half of the input Ri and the sub-key Ki. The output of the XORing operation is sent to a substitution box, and the output of the S-boxes is sent to a permutation process. Finally, the output is XORed with the left half to create the right half input for the next round. The right half of the input Ri became the left half of the next round's input, as shown in Equations 1 and 2.

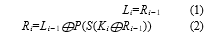
SLIM has addressed previous work constraints and limitations such as S-boxes trapdoors, memory size, speed, look-up tables, P-boxes, key size, complexity, software, and hardware implementations.

B. Substitution Layer

One of the most difficult challenges in cryp- tography is designing S-boxes. Because they are the sole non-linear component in the most current algorithms, they can be regarded the cornerstone of all cryptosystems. As a result, the algorithm as a whole suffers from the poor design of S-boxes. In 1991, Biham [27] proposed differential cryptanalysis, which is based on the presence of DES S-boxes trapdoor vulnerabilities. Furthermore, utilizing the same trapdoors in the S-boxes, Matsui was able to re-attack DES and minimize the time it took to crack it using a linear cryptanalysis approach.As a result, S-boxes must be carefully constructed or selected. SLIM uses the S-box (see Table 4) which is repeated four times in parallel to achieve a small footprint. The S-box must be robust enough to survive linear and differential attacks while still being one of the smallest 4-bit S-boxes [2]. The substitution layer is decided by the linear and differential cryptanalysis of the encryption.

C. Permutation Layer

Permutation is a broad term for rearrangement. In this case, the permutation is the SLIM function's final phase. The permutation box accepts 16-bit inputs and permutes them using a set of rules to produce a 16-bit output. When there is no fixed point, the permutation process is detailed in Table 5 to avoid linearity analysis. The permutation layer is determined depending on the cipher's linear and differential cryptanalysis.

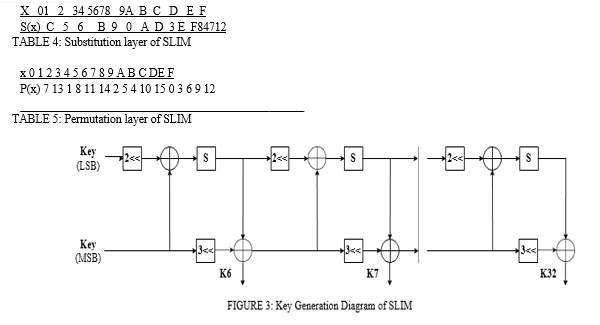
C. Key Generation

32 sub-keys (16 bits) are required for 32 rounds and a 32-bit block, which are created from the 80-bit encryption key (see Figure 3). The following is the generation scheme:

1. The first five sub-keys, labelled K1, K2, and K5, are immediately extracted from the original key, with K1 corresponding to the first (least important) 16-bits, K2 to the next 16, and so on. The 80-bit key is then split in half by a splitter, yielding two 40-bit values labelled KeyMSB and KeyLSB, which are then processed individually.
2. KeyLSB conducts a two-bit circular left shift at the conclusion of each cycle, and the resulting output is XORed by KeyMSB. The output of the XORing process is transferred to a substitution layer. The output of the S- boxes and the rotated KeyMSB (KeyMSB 3) are merged using the XOR technique to form the round sub-key.

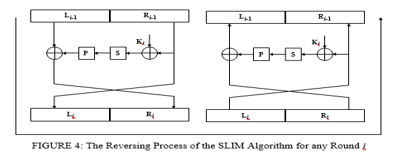
D. Slim Decryptionstructure

The decryption procedure is the same as the encryption process. The same SLIM structure is used for SLIM decryption, but the decryption sub-key is applied in the reverse order, with a different sub-key option. Figure 4 depicts the reverse procedure for both encryption and decryption of round i. Like any symmetric encryption technique, the decryption round structure is comparable to that of encryption. The encryption procedure with the Ki subkey is shown on the left-hand side of Figure 4. In the round output, the coded message is represented by n-bits. On the other hand, the decryption procedure employing the same sub-key Ki is shown on the right side of Figure 4. The round function comes after the other functions in the sequence. In the round output, the original message is represented by n-bits.

IV. IMPLEMENTATION CONSIDERATIONS OFTHE PROPOSED SLIMALGORITHM

As previously stated, the goal of SLIM is to make software and hardware implementation more straightforward. Software implementation is less expensive and more platform-agnostic than hardware implementation. The concepts of software implementation are as follows:

1. Use of sub-blocks: For faultless cipher operations, they must use sub-blocks that are suitable and natural for software in the shape of 4, 8, 16, or 32 bits. Because SLIM can employ either 4 or 16-bit sub-blocks, this is a simple task.
2. Use basic operations: It should be simple to programme addition, subtraction, shifting, complementing, XORing, and other operations. The components of SLIM also meet this requirement.

The following are the hardware implementation design concepts:

a. Encryption and decryption are similar: The only difference between encryption and decryption should be how the key is used, allowing the same device to perform both tasks. The structure of SLIM meets this requirement. as well as the expenses of implementation SLIM employs four 4 4 S-shaped S-shapedS-shapedS-shapedS-shaped S- • Using small S-boxes might help you conserve memory space.

b. Regular structure: For VLSI implementation, the cipher should have a regular structure. SLIM is made up of just one simple modular construction component that can be reused many times.

A. Hardware Implementation Of The Proposed Slim Algorithm

A round-based SLIM implementation is simple to make, however a serialised SLIM implementation poses some challenges to a hardware designer. Focus on the later, which has a 4 bit data path width, rather than the older design's complexities. The permutation stage is the most difficult because it permutes the entire state. As a result, operations on 4-bit chunks are no longer feasible; instead, operations on the complete state (16-bit) are used. Processing all components of the state and conducting one round of SLIM requires four clock cycles in the suggested architecture depicted in Figure 5. Then, for one clock cycle, swapping the contents of the registers as the Feistel structure requires, i.e. acting on the full state. This clock cycle had been used for the permutation operation, but in the proposed design, both halves of the state had already been XORed. As a result, the right halve of prior clock cycles was reversed before being stored as the new left halve. After the XOR total of both halves is permuted, the final step of one SLIM cycle is performed. The following operations are performed when the contents of the registers are swapped:

The circuit area in GE required for the SLIM lightweight cipher is determined using the standard ASIC library IBM 8RF (0.130 ms). D-flip-flops for storing the key and data state, which are standard library values for various gates, take up the space required in the aforementioned implementation. The storage of an 80-bit key takes about 340 GE, while the storage of a 32-bit data state takes about 136 GE [28]. The following are the three sub-functions that make up the circular structure: (XOR, S-box, and permutation).

1. Add Round Key: The SLIM key addition technique uses a 4-bit XOR operation to complete this mixing procedure, which takes around a minute (7.5 GE).
2. Substitution-layer: The non-linear S-box layer in the serial implementation of SLIM is made up of a single 4-bit S-box, which takes up about a megabyte (27 GE).
3. Diffusion-layer: A permutation process is conducted at the end of each SLIM round function, which is simple to implement and takes up no space.

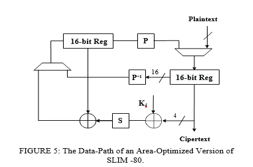
Finally, both halves' extra modulo 2 necessitates a 4-bit XOR operation, which necessitates (7.5 GE). Furthermore, the normal round of SLIM necessitates two 2-to-1 MUXes to select between the input data (plaintext) and the output that emerges at the bottom of the preceding round's data-path; a single 2-to-1 MUX process necessitates (2 2.25 = 4.5 GE). As a result, Table 6 was 2.25 GE. As a result of the multiplexing (selecting), the full encryption process region is represented in gate equivalents.

Figure 6 depicts the fundamental scheduling architecture. The key generator structure is made up of the three sub-functions listed below (XOR, S-box, and shifting).

a. Shifting Procedure: In SLIM, the key segments' right-hand sides (LSBs) are sent via a two-step left circular shifting process that does not require any gates. The key segments' left-hand side (MSBs) are passed through a three-step left circular shifting process that does not require any gates.

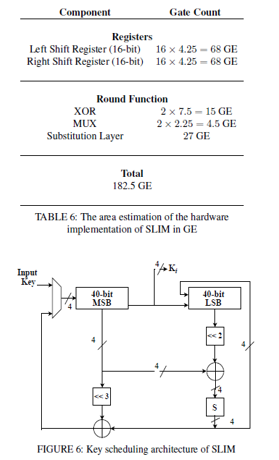
b. Substitution-layer: In SLIM, the Single S-box is used for key scheduling to reduce datapath implementation overhead. The non-linear S-box layer, shown in Figure 7, is made up of a single 4-bit S-box (4-AND, 4-XOR) that takes roughly a second to compute (13 GE).

c. XORing Process: The key generator requires two 4-bit XOR operations to alter the distinct inputs in SLIM, which takes roughly (2 7.5 = 13 GE).

Finally, a single 2-to-1 MUX is required to pick between the input key and the result that appears at the bottom of the preceding round's data-path; a single 2-to-1 MUX costs 2.25 GE. As a result, Table 7 shows GE's primary scheduling calculations for this architecture's hardware implementation.

V. ANALYSIS OF THE PROPOSED SLIMALGORITHM

The cryptographic strength features of the SLIM are as follows, as shown in this section:

1. Block Length: The block length should be long enough to avoid statistical analysis. This also applies to SLIM, which use a 32-bit block.
2. Key Length: The key length should be long enough to avoid lengthy key searches. SLIM is secure in this region for the time being, thanks to its 80-bit length.
3. Confusion: The ciphertext should be based on the plaintext and key in a complicated and related manner. The goal is to make it more difficult to determine how plaintext statistics affect ciphertext statistics. A powerful 4-bit S-box is used by SLIM to do this.
4. Diffusion: Each plaintext bit should affect each ciphertext bit, and each key bit should affect each ciphertext, allowing the plaintext statistical structure to be spread across several ciphertext bits. SLIM utilises a permutation method in addition to interchanging the two halves of the plaintext each round. This structure takes two (n/2)-bit plaintext values as input and produces two (n/2)-bit sub-keys from the key. Each output bit is dependent on each plaintext input bit and each sub-key bit in the first round. This core structure is repeated m times by the algorithm.

Table 8 compares the results of SLIM's hardware implementation to those of other algorithms. Because they are lightweight block ciphers built on 0.13m technol- vary on the kind of FF, technology, library, and other factors [9], the statistics should be treated with caution. The ogy has been captured on tape. The table also includes Gates/Memory Bit, which indicates the size (in GE) of the 1-bit memory device used for the key and states. SPECK32-64 has a smaller implementation area, but it only uses a 64-bit key.

VI. CRYPTANALYSIS OFSLIM

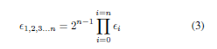
Linear and differential cryptanalysis are the most significant cryptanalytic tools. In all cryptanalysis methodologies, the attacker tries to find a linear or differential path through the multiple rounds of cipher. Finding an optimal approach is the most difficult problem of such assaults due to the large search space of choices. Dwivedi et al. [36] proposed a Nested search based heuristic strategy to locate the differential path in many block ciphers. However, applying such a technique directly to any cipher is not as simple as plugging it in; it necessitates a high level of coding expertise to alter the cipher in the needed format. In most block ciphers, such approaches may be used to discover the linear or differential route.The code is written in Python and can be found on GitHub [37] by clicking here.

A. Linear Crypt Analysis

Matsui [38] invented linear cryptanalysis in 1993, and it has since become the most powerful method for decrypting any encryption. The primary idea is to approximate the relationship between plaintext (input) and ciphertext (output) bits using a linear approximation. Such a link should hold with probability 0.5 (bias = 0) for a safe cipher. If an attacker can find a relationship where bias 6=0, it could be turned into an attack. To find linear paths in cipher, first make a linear approximation table for the S-box. In each round, the Nested approach tries to find the best bias from the approximation table and offer the best path. Matsui presented a formula for estimating total bias in his paper [38]. The differential path (see Table 9) could only be determined for the first 11 rounds, so cipher is safe for the total number of rounds.

B. Differential Crypt Analysis

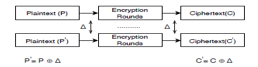
Biham et al. [27] presented One of the most powerful approaches for decrypting any encryption is differential cryptanalysis. In the case of a selected plaintext ciphertext situation, when an intruder can access the encrypted text by selecting any plaintext as the cipher's input, differential cryptanalysis is performed. To do differential cryptanalysis, the attacker must first get a pair of plaintexts with a constant difference between them. The mismatch could be due to a 2n modular addition or an XOR operation (see Figure 8).

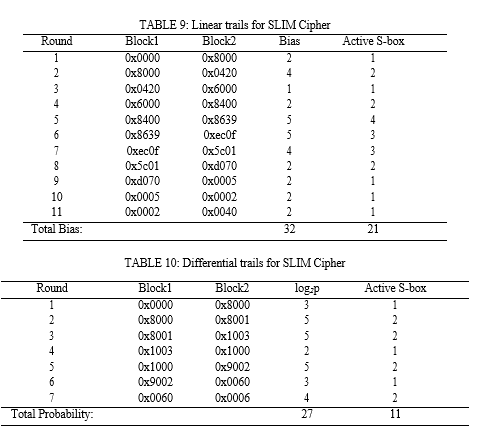
A distinct path (sometimes called a trail or a characteristic) is a set of variations formed by cipher encryption over multiple rounds. Attackers are mostly interested in non-linear components when hunting for the differential path (in this example, the S-box). There could be several output differences for a given input difference (through Sbox). As a result, the attacker builds an S-box difference distribution table that shows the likelihood of a specific output over another. We adopted the Nested tree search heuristic technique suggested by Dwivedi et al. [39], [40] to locate a differential path in SLIM in this research. To begin, we created a difference distribution table based on S-box criteria and attempted to design a differential path using that table. We were only able to identify the differential path (see Table 10) for the first seven rounds, hence the encryption is safe for the entire amount of rounds.

Conclusion

SLIM is a novel ultra-lightweight cryptography technique for RFID devices introduced in this research. RFID systems are susceptible to a variety of cyber-threats. The most difficult problem with RFID systems is ensuring effective resistance against these assaults. Because they require a lot of CPU power, memory, and resources to execute, modern encryption algorithms optimized for maximum devices are not appropriate for RFID systems. In RFID systems, the amount of available cryptographic storage space is restricted, and the amount of power that may be consumed is severely limited. Lightweight cryptographic algorithms are one of the most acceptable solutions for protecting information in these scenarios. The proposed SLIM ultra-lightweight cryptography solution is well suitable for use in RFID systems that have limitations. SLIM is a block cipher with a 32-bit block size based on a Feistel structure. SLIM uses a long key length of 80 bits to avoid exhaustive key searches. To investigate how ciphertext statistics rely on plaintext statistics, SLIM employs a strong four fourfour substitution box. With a small implementation area of just 553 GE, an appropriate cost/security for RFID devices, and energy-efficient behaviour, the suggested algorithm performs well in both hardware and software settings. SLIM has demonstrated strong immunity and a considerable protection margin against the most successful linear and differential cryptanalysis attacks. The suggested technique is appropriate for wireless networks, particularly Wireless Sensor Networks (WSNs) and Internet of Things (IoT) applications, where data transmissions are often only a few bytes long. In comparison to other known and implemented algorithms, SLIM proved to be extremely efficient.In the future, SLIM will be installed on a healthcare IoT framework in order to assess it for sensitive applications.

References

REFERENCES [1] W. Wu and L. Zhang, “Lblock: A lightweight block cipher,” in Applied Cryptography and Network Security - 9th International Conference, ACNS 2011, Nerja, Spain, June 7-10, 2011. Proceedings (J. López and G. Tsudik, eds.), vol. 6715 of Lecture Notes in Computer Science, pp. 327–344, 2011. [2] A. Bogdanov, L. R. Knudsen, G. Leander, C. Paar, A. Poschmann, M. J. B. Robshaw, Y. Seurin, and C. Vikkelsoe, “PRESENT: an ultra-lightweight block cipher,” in Cryptographic Hardware and Embedded Systems - CHES 2007, 9th International Workshop, Vienna, Austria, September 10-13, 2007, Proceedings (P. Paillier and I. Verbauwhede, eds.), vol. 4727 of Lecture Notes in Computer Science, pp. 450–466, Springer, 2007. [3] C. H. Lim and T. Korkishko, “mcrypton - A lightweight block cipher for security of low-cost RFID tags and sensors,” in Information Security Applications, 6th International Workshop, WISA 2005, Jeju Island, Korea, August 22-24, 2005, Revised Selected Papers (J. Song, T. Kwon, and M. Yung, eds.), vol. 3786 of Lecture Notes in Computer Science, pp. 243– 258, Springer, 2005 [4] K. Shibutani, T. Isobe, H. Hiwatari, A. Mitsuda, T. Akishita, and T. Shirai, “Piccolo: An ultra-lightweight blockcipher,” in Cryptographic Hardware and Embedded Systems - CHES 2011 - 13th International Workshop, Nara, Japan, September 28 - October 1, 2011. Proceedings (B. Preneel and T. Takagi, eds.), vol. 6917 of Lecture Notes in Computer Science, pp. 342–357, Springer, 2011. [5] L. Batina, A. Das, B. Ege, E. B. Kavun, N. Mentens, C. Paar, I. Ver- bauwhede, and T. Yalçin, “Dietary recommendations for lightweight block ciphers: Power, energy and area analysis of recently developed architec- tures,” in Radio Frequency Identification - Security and Privacy Issues 9th International Workshop, RFIDsec 2013, Graz, Austria, July 9-11, 2013, Revised Selected Papers (M. Hutter and J. Schmidt, eds.), vol. 8262 of Lecture Notes in Computer Science, pp. 103–112, Springer, 2013. [6] J. Daemen and V. Rijmen, The Design of Rijndael: AES - The Advanced Encryption Standard. Information Security and Cryptography, Springer, 2002. [7] D. J. Wheeler and R. M. Needham, “Tea, a tiny encryption algorithm,” in Fast Software Encryption: Second International Workshop. Leuven, Belgium, 14-16 December 1994, Proceedings (B. Preneel, ed.), vol. 1008 of Lecture Notes in Computer Science, pp. 363–366, Springer, 1994. [8] D. Hong, J. Sung, S. Hong, J. Lim, S. Lee, B. Koo, C. Lee, D. Chang, J. Lee, K. Jeong, H. Kim, J. Kim, and S. Chee, “HIGHT: A new block cipher suitable for low-resource device,” in Cryptographic Hardware and Embedded Systems - CHES 2006, 8th International Workshop, Yokohama, Japan, October 10-13, 2006, Proceedings (L. Goubin and M. Matsui, eds.), vol. 4249 of Lecture Notes in Computer Science, pp. 46–59, Springer, 2006. [9] C. D. Cannière, O. Dunkelman, and M. Knezevic, “KATAN and KTAN- TAN - A family of small and efficient hardware-oriented block ciphers,” in Cryptographic Hardware and Embedded Systems - CHES 2009, 11th International Workshop, Lausanne, Switzerland, September 6-9, 2009, Proceedings (C. Clavier and K. Gaj, eds.), vol. 5747 of Lecture Notes in Computer Science, pp. 272–288, Springer, 2009. [10] T. Sugawara, N. Homma, T. Aoki, and A. Satoh, “High-performance ASIC implementations of the 128-bit block cipher CLEFIA,” in International Symposium on Circuits and Systems (ISCAS 2008), 18-21 May 2008, Sheraton Seattle Hotel, Seattle, Washington, USA, pp. 2925–2928, IEEE, 2008. [11] Z. Gong, S. Nikova, and Y. W. Law, “KLEIN: A new family of lightweight block ciphers,” in RFID. Security and Privacy - 7th International Work- shop, RFIDSec 2011, Amherst, USA, June 26-28, 2011, Revised Selected Papers (A. Juels and C. Paar, eds.), vol. 7055 of Lecture Notes in Computer Science, pp. 1–18, Springer, 2011. [12] L. R. Knudsen, G. Leander, A. Poschmann, and M. J. B. Robshaw, “Printcipher: A block cipher for ic-printing,” in Cryptographic Hardware and Embedded Systems, CHES 2010, 12th International Workshop, Santa Barbara, CA, USA, August 17-20, 2010. Proceedings (S. Mangard and F. Standaert, eds.), vol. 6225 of Lecture Notes in Computer Science, pp. 16–32, Springer, 2010. [13] F. Standaert, G. Piret, N. Gershenfeld, and J. Quisquater, “SEA: A scalable encryption algorithm for small embedded applications,” in Smart Card Research and Advanced Applications, 7th IFIP WG 8.8/11.2 Interna- tional Conference, CARDIS 2006, Tarragona, Spain, April 19-21, 2006, Proceedings (J. Domingo-Ferrer, J. Posegga, and D. Schreckling, eds.), vol. 3928 of Lecture Notes in Computer Science, pp. 222–236, Springer, 2006. [14] G. Leander, C. Paar, A. Poschmann, and K. Schramm, “New lightweight DES variants,” in Fast Software Encryption, 14th International Workshop, FSE 2007, Luxembourg, Luxembourg, March 26-28, 2007, Revised Se- lected Papers (A. Biryukov, ed.), vol. 4593 of Lecture Notes in Computer Science, pp. 196–210, Springer, 2007. [15] J. Aumasson, L. Henzen, W. Meier, and M. Naya-Plasencia, “Quark: A lightweight hash,” J. Cryptology, vol. 26, no. 2, pp. 313–339, 2013. [16] A. Bogdanov, M. Knezevic, G. Leander, D. Toz, K. Varici, and I. Ver- bauwhede, “spongent: A lightweight hash function,” in Cryptographic Hardware and Embedded Systems - CHES 2011 - 13th International Workshop, Nara, Japan, September 28 - October 1, 2011. Proceedings (B. Preneel and T. Takagi, eds.), vol. 6917 of Lecture Notes in Computer Science, pp. 312–325, Springer, 2011. [17] G. Bertoni, J. Daemen, M. Peeters, and G. Van Assche, “Keccak Sponge Function Family Main Document.” http://keccak.noekeon.org/ Keccak-main-2.1.pdf. [18] A. Y. Poschmann, Lightweight cryptography: cryptographic engineering for a pervasive world. PhD thesis, Ruhr University Bochum, 2009. [19] S. Badel, N. Dagtekin, J. N. Jr., K. Ouafi, N. Reffé, P. Sepehrdad, P. Susil, and S. Vaudenay, “ARMADILLO: A multi-purpose cryptographic prim- itive dedicated to hardware,” in Cryptographic Hardware and Embedded Systems, CHES 2010, 12th International Workshop, Santa Barbara, CA, USA, August 17-20, 2010. Proceedings (S. Mangard and F. Standaert, eds.), vol. 6225 of Lecture Notes in Computer Science, pp. 398–412, Springer, 2010. [20] A. Bogdanov, G. Leander, C. Paar, A. Poschmann, M. J. B. Robshaw, and Y. Seurin, “Hash functions and RFID tags: Mind the gap,” in Cryptographic Hardware and Embedded Systems - CHES 2008, 10th International Workshop, Washington, D.C., USA, August 10-13, 2008. Proceedings (E. Oswald and P. Rohatgi, eds.), vol. 5154 of Lecture Notes in Computer Science, pp. 283–299, Springer, 2008. [21] J. Guo, T. Peyrin, and A. Poschmann, “The PHOTON family of lightweight hash functions,” in Advances in Cryptology - CRYPTO 2011-31st Annual Cryptology Conference, Santa Barbara, CA, USA, August 14-18, 2011. Proceedings (P. Rogaway, ed.), vol. 6841 of Lecture Notes in Computer Science, pp. 222–239, Springer, 2011. [22] D. Watanabe, T. Owada, K. Okamoto, Y. Igarashi, and T. Kaneko, “Update on enocoro stream cipher,” in Proceedings of the International Symposium on Information Theory and its Applications, ISITA 2010, 17-20 October 2010, Taichung, Taiwan, pp. 778–783, IEEE, 2010. [23] M. Feldhofer and J. Wolkerstorfer, Hardware Implementation of Symmet- ric Algorithms for RFID Security, pp. 373–415. Springer, 1 ed., 2008. [24] S. L. Garfinkel, A. Juels, and R. Pappu, “RFID privacy: An overview of problems and proposed solutions,” IEEE Secur. Priv., vol. 3, no. 3, pp. 34– 43, 2005. [25] A. Poschmann, G. Leander, K. Schramm, and C. Paar, “New light-weight crypto algorithms for RFID,” in International Symposium on Circuits and Systems (ISCAS 2007), 27-20 May 2007, New Orleans, Louisiana, USA, pp. 1843–1846, IEEE, 2007. [26] R. M. Needham and D. J. Wheeler, “Tea extensions.” http://www.cix.co. uk/~klockstone/xtea.pdf, 1997. Accessed on 2020-08-30. [27] E. Biham and A. Shamir, “Differential cryptanalysis of des-like cryptosys- tems,” J. Cryptology, vol. 4, no. 1, pp. 3–72, 1991. [28] R. Beaulieu, D. Shors, J. Smith, S. Treatman-Clark, B. Weeks, and L. Wingers, “The SIMON and SPECK lightweight block ciphers,” in DAC, pp. 175:1–175:6, ACM, 2015. [29] V. Grosso, G. Leurent, F. Standaert, and K. Varici, “Ls-designs: Bitsliceen- cryption for efficient masked software implementations,” in Fast Software Encryption - 21st International Workshop, FSE 2014, London, UK, March 3-5, 2014. Revised Selected Papers (C. Cid and C. Rechberger, eds.), vol. 8540 of Lecture Notes in Computer Science, pp. 18–37, Springer, 2014. [30] P. Hämäläinen, T. Alho, M. Hännikäinen, and T. D. Hämäläinen, “Design and implementation of low-area and low-power AES encryption hardware core,” in Ninth Euromicro Conference on Digital System Design: Archi- tectures, Methods and Tools (DSD 2006), 30 August - 1 September 2006, Dubrovnik, Croatia, pp. 577–583, IEEE Computer Society, 2006. [31] T. Akishita and H. Hiwatari, “Very compact hardware implementations of the blockcipher CLEFIA,” in Selected Areas in Cryptography - 18th International Workshop, SAC 2011, Toronto, ON, Canada, August 11-12, 2011, Revised Selected Papers (A. Miri and S. Vaudenay, eds.), vol. 7118 of Lecture Notes in Computer Science, pp. 278–292, Springer, 2011. [32] J. Borghoff, A. Canteaut, T. Güneysu, E. B. Kavun, M. Knezevic, L. R. Knudsen, G. Leander, V. Nikov, C. Paar, C. Rechberger, P. Rombouts, S. S. Thomsen, and T. Yalçin, “PRINCE - A low-latency block cipher for pervasive computing applications (full version),” IACR Cryptol. ePrint Arch., vol. 2012, p. 529, 2012. [33] J. Guo, T. Peyrin, A. Poschmann, and M. J. B. Robshaw, “The LED block cipher,” in Cryptographic Hardware and Embedded Systems - CHES 2011-13th International Workshop, Nara, Japan, September 28 - October 1, 2011. Proceedings (B. Preneel and T. Takagi, eds.), vol. 6917 of Lecture Notes in Computer Science, pp. 326–341, Springer, 2011. [34] T. Plos, C. Dobraunig, M. Hofinger, A. Oprisnik, C. Wiesmeier, and J. Wiesmeier, “Compact hardware implementations of the block ciphers mcrypton, noekeon, and SEA,” in Progress in Cryptology - INDOCRYPT 2012, 13th International Conference on Cryptology in India, Kolkata, India, December 9-12, 2012. Proceedings (S. D. Galbraith and M. Nandi, eds.), vol. 7668 of Lecture Notes in Computer Science, pp. 358–377, Springer, 2012. [35] W. Zhang, Z. Bao, D. Lin, V. Rijmen, B. Yang, and I. Verbauwhede, “RECTANGLE: A bit-slice ultra-lightweight block cipher suitable for multiple platforms,” IACR Cryptol. ePrint Arch., vol. 2014, p. 84, 2014. [36] D. A. Dhar, P. Morawiecki, and S. Wójtowicz, “Finding differential paths in arx ciphers through nested monte-carlo search,” International Journal of Electronics and Telecommunications, vol. vol. 64, no. No 2, 2018. [37] A. D. Dwivedi, “Slim: An ultra-lightweight block cipher algorithm suit- able for rfid systems.” Available at https://github.com/ashudhar7/Agile, 2020. [38] M. Matsui, “Linear cryptanalysis method for DES cipher,” in Advances in Cryptology - EUROCRYPT ’93, Workshop on the Theory and Application of of Cryptographic Techniques, Lofthus, Norway, May 23-27, 1993, Proceedings, pp. 386–397, 1993. [39] A. D. Dwivedi and G. Srivastava, “Differential cryptanalysis of round- reduced LEA,” IEEE Access, vol. 6, pp. 79105–79113, 2018. [40] A. D. Dwivedi, “Security analysis of lightweight iot cipher: Chaskey,” Cryptography, vol. 4, no. 3, 2020.

Copyright

Copyright © 2022 Ankit Ruhil, Dr. Manjot Kaur Bhatia, Pooja kumari. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.