Solving Economic Load Dispatch Problem Using Grey Wolf Optimization Algorithm

Abstract

This article presents a new evolutionary optimization approach named grey wolf optimization (GWO), which is based on the behavior of grey wolves, for the optimal operating strategy of economic load dispatch (ELD). Nonlinear characteristics of generators like ramp rate limits, valve point discontinuities and prohibited operating zones are considered in the problem. GWO method does not require any information about the gradient of the objective function, while searching for an optimum solution. The GWO algorithm concept appears to be a robust and reliable optimization algorithm is applied to the nonlinear ELD problems. The proposed algorithm is implemented and tested on two test systems having 40 Thermal generators. The results confirm the potential and effectiveness of the proposed algorithm compared to various other methods available in the literature. The outcome is very encouraging and proves that the GWO is a very effective optimization technique for solving various ELD problems.

Introduction

I. INTRODUCTION

Economic load dispatch (ELD) is a process used in power systems to determine the optimal distribution of power output from various generating units to meet the system demand while minimizing the operating costs. This is achieved by optimizing the output of each generator in the system, subject to the operating constraints of the system such as transmission capacity, voltage limits, and stability limits. The ELD problem is a nonlinear optimization problem that requires solving a set of equations to determine the optimal operating point for each generator. The solution is typically obtained using mathematical optimization techniques such as linear programming; nonlinear programming but these mathematical methods are having various disadvantages such as the increased computational complexity of techniques with the size and complexity of the problem. As a result, it may be difficult or even impossible to solve large-scale non convex optimization problems using these techniques. On the other hand, heuristic optimization methods can handle nonlinear and non-convex problems effectively by searching the solution space using a population of solutions and applying evolutionary operators such as mutation, crossover, and selection etc., also ELD problems involve multiple constraints such as power balance, generator output limits, transmission capacity limits, and voltage limits.

Evolutionary algorithm can handle multiple constraints by incorporating penalty functions or constraints handling techniques into the fitness function. In recent literature various heuristic algorithms are reported to solve the ELD problems.  Gaing proposed particle swarm optimization (PSO) to solve the ELD problem in power systems and compared with Genetic Algorithm. Several nonlinear characteristics of the generator such as ramp rate limits, POZs and non-smooth cost functions were considered [1]. In [2], Firefly algorithm [FA] was used to determine optimal solution  for the ELD problems FA emulates social conduct of fire flies dependent on their blazing  quality. Dubey, pandit and panigrahi [3] presented modified flower pollination algorithm [MFPA]  to deal the  ELD problems. In the MFPA neighborhood fertilization of FPA was constrained by a scaling component and a concentrated exploitation stage was added to determine the best solutions. A continuous version of quick group search optimizer (QGSO) algorithm was proposed to realize me ELD formulation with VPL effect POZs, transformation losses and ramp rate limits [4]. Cuckoo search algorithm (CSA) was developed for solving both convex and non-convex ELD problems [5]. It was inspired from the obligate brood parasitism of some cuckoo species by laying their eggs in the nests of other host birds of different species. Simulated annealing technique has been applied to determine the optimal generation schedule for economic dispatch problems in a power system [6]. Hybrid evolutionary programming (HEP) [14] is used to obtain best optimal solution.[7]. In [8] authors used Evolutionary programming method for solving ELD problems .

This paper presents a new swarm based optimization algorithm known as Gray wolf optimization (GWO) developed by  proposed by Mirjalili et al. in 2014 [9]. This algorithm is inspired by the hunting nature of the gray wolf. To assess the effectiveness of the GWO, Two test system having different constraints are taken in to consideration and optimized for best optimal fuel cost. Obtained results are compared with the other heuristic methods in the literature.

Organization of this research article as follows: In Section 2, the formulation of the economic load dispatch problem is discussed. In Section 3, the applied Gray wolf optimization algorithm is explained, as well as its implementation process for the ELD problem. In Section 4, Simulation results are presented to compare GWO’s effectiveness to that of the original algorithm and other algorithms. Final section summarizes this research work.

D. Attacking prey (exploitation)

The grey wolves stop the hunting by attacking the prey when it stop moving. It depends on the value of a* AM is a random value in the interval [-2a, 2a]. In GWO, search agents update their positions based on the location of alpha, beta, delta wolves mentioned in hunting phase and attack towards the prey.

E. Grey wolf optimization applied to ELD

The different steps of GWO algorithm for solving ELD problems are described below.

1. Step 1: Active power generation of all the generating units initialized randomly within their lower and upper real power operating limits
2. Step 2: Evaluate fitness of each solution of current population using (1)–(3). Each fitness value represents the distance of the individual wolf from the prey.
3. Step 3: Sort the population from best to worst. The best, second best and third best solutions respectively, represent the positions of ????, β and δ categories of wolves.
4. Step 4: Modify the position of each search agents using the searching prey, encircling prey, hunting and attacking prey concepts. The position of each search agent represents a potential solution comprised of active power generation of ELD problem.
5. Step 5: Check whether the operating limits of the active power of all generating units except last unit are violated or not. If any power generation is less than the minimum level, it is made equal to minimum value. Similarly, if it is greater than the maximum level, it is assigned its maximum value. Subsequently, last unit of the power generation is evaluated using (5) and whether it satisfies all the inequality constraints or not is checked. The infeasible solutions are exchanged by the best feasible solutions.
6. Step 6: Go to Step 2 until termination criteria is met. The GWO is stopped executing when the maximum number of iterations (generations) is reached or there is no noteworthy improvement in the solution. In this paper, the ending criterion is the maximum number of iterations for which most of the grey wolves or search agents are idle.

IV. CASE STUDIES AND NUMERICAL RESULTS

In order to validate the feasibility of the proposed GWO method for the ELD problems, it is employed on a relatively large system consisting of 40 generating units. The load demand used in the simulations is 10500 MW. In order to judge the efficacy of the proposed in nonlinear environment, the valve-point effect and prohibited operating zones are considered. Data for the test system is referred from [10]. The developed algorithm is simulated and tested in MATLAB 7.1 Software on 2 GHz Pentium IV, 1 GB RAM personal computer. The population size and the maximum iteration number are taken as 50 and 500 respectively for the test systems under consideration.

Test Case 1: 40-unit system without valve point loading effect and without Transmission loss.

Test Case 2: 40-unit system including valve point loading effect and Transmission Loss.

A Test System 1

In this 40 unit test system Valve point effects and Transmission losses are not considered for the simulation. The results obtained by applying the GWO algorithm and other heuristic method known as variable scaling hybrid differential evolution (VSHDE) [11]  are summarized in Table 1 for 40-unit power system without considering the effects of valve-point loading without transmission losses. Analyzing the data, it can be observed that the GWO method succeeds in finding a satisfactory solution.

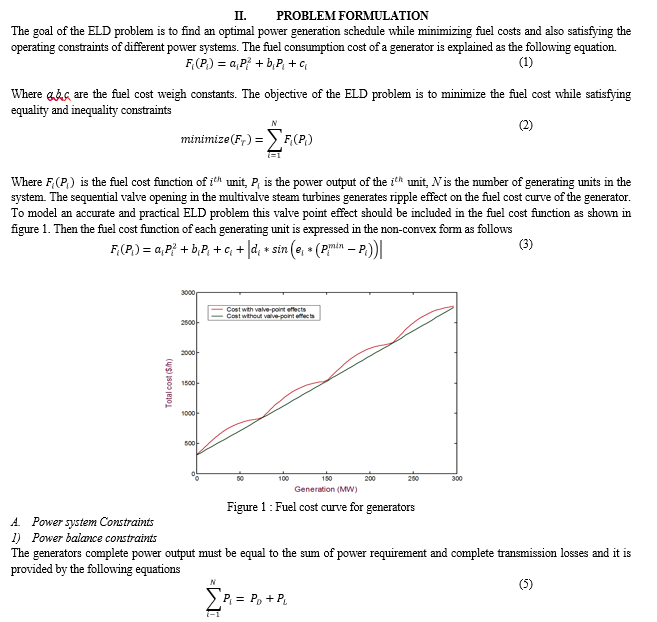
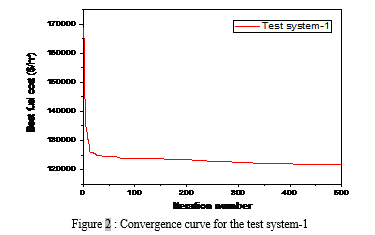
The minimum cost obtained by the proposed GWO method was given by 121244 $/hr, which is the best cost found so far. The analysis of these comparative results demonstrates that the proposed approach shows superior performance compared to other method reported in the literature. Convergence curve for this test system is shown in figure 3.

Table 1 : Best fuel cost Simulation test results for the Test system 1

B. Test system 2

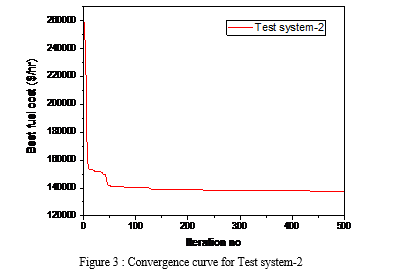
The simulation results obtained by proposed GWO method for 40- unit test system considering transmission losses and valve point loading effects are compared with GA-API [12],SDE [10],TLBO [13] in Table 2. From Table 2, it was observed that GWO outperforms other optimization methods. In this case, the GWO obtained total cost 2267.8 $/hr, 560.3 $/hr, 217 $/hr lesser than the GA-API, SDE, and TLBO algorithms respectively. Convergence curve for this test system is shown in figure 3. The simulation results clearly suggest that GWO produces feasible solutions. To judge the superiority and robustness,

Table 2 : Best fuel cost Simulation test results for the Test system 1

Conclusion

In this work, an efficient meta-heuristic algorithm named GWO is proposed to solve the ELD problem taking the valve point loading effects, prohibited operating zone, ramp rate limits into consideration. Two case studies are employed to demonstrate the applicability of the GWO method. The benefit of the proposed GWO is that it does not impose any convexity limitations on the generating unit characteristics. Numerical results show that the GWO method has superior features, advantages over other algorithms in terms of robustness, avoids premature convergence, simple applicability and stable convergence characteristic. Although, the proposed algorithm is applied to solve ELD problems in the current study, it seems from its unique feature that GWO has the potential to solve many other optimization problems in the field of power system planning and operation.

References

[1] Z.-L. Gaing, “Particle swarm optimization to solving the economic dispatch considering the generator constraints,” IEEE Trans. Power Syst., vol. 18, no. 3, pp. 1187–1195, Aug. 2003, doi: 10.1109/TPWRS.2003.814889. [2] X.-S. Yang, S. S. Sadat Hosseini, and A. H. Gandomi, “Firefly Algorithm for solving non-convex economic dispatch problems with valve loading effect,” Appl. Soft Comput., vol. 12, no. 3, pp. 1180–1186, Mar. 2012, doi: 10.1016/j.asoc.2011.09.017. [3] H. M. Dubey, M. Pandit, and B. K. Panigrahi, “A Biologically Inspired Modified Flower Pollination Algorithm for Solving Economic Dispatch Problems in Modern Power Systems,” Cognit. Comput., vol. 7, no. 5, pp. 594–608, Oct. 2015, doi: 10.1007/s12559-015-9324-1. [4] M. Moradi-Dalvand, B. Mohammadi-Ivatloo, A. Najafi, and A. Rabiee, “Continuous quick group search optimizer for solving non-convex economic dispatch problems,” Electr. Power Syst. Res., vol. 93, pp. 93–105, Dec. 2012, doi: 10.1016/j.epsr.2012.07.009. [5] M. Basu and A. Chowdhury, “Cuckoo search algorithm for economic dispatch,” Energy, vol. 60, pp. 99–108, Oct. 2013, doi: 10.1016/j.energy.2013.07.011. [6] K. P. Wong and C. C. Fung, “Simulated annealing based economic dispatch algorithm,” IEE Proc. C Gener. Transm. Distrib., vol. 140, no. 6, p. 509, 1993, doi: 10.1049/ip-c.1993.0074. [7] A. K. Swain and A. S. Morris, “A novel hybrid evolutionary programming method for function optimization,” in Proceedings of the 2000 Congress on Evolutionary Computation. CEC00 (Cat. No.00TH8512), pp. 699–705, doi: 10.1109/CEC.2000.870366. [8] Hong-Tzer Yang, Pai-Chuan Yang, and Ching-Lien Huang, “Evolutionary programming based economic dispatch for units with non-smooth fuel cost functions,” IEEE Trans. Power Syst., vol. 11, no. 1, pp. 112–118, 1996, doi: 10.1109/59.485992. [9] S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey Wolf Optimizer,” Adv. Eng. Softw., vol. 69, pp. 46–61, Mar. 2014, doi: 10.1016/j.advengsoft.2013.12.007. [10] A. Srinivasa Reddy and K. Vaisakh, “Shuffled differential evolution for large scale economic dispatch,” Electr. Power Syst. Res., vol. 96, pp. 237–245, Mar. 2013, doi: 10.1016/j.epsr.2012.11.010. [11] J.-P. Chiou, “Variable scaling hybrid differential evolution for large-scale economic dispatch problems,” Electr. Power Syst. Res., vol. 77, no. 3–4, pp. 212–218, Mar. 2007, doi: 10.1016/j.epsr.2006.02.013. [12] I. Ciornei and E. Kyriakides, “A GA-API Solution for the Economic Dispatch of Generation in Power System Operation,” IEEE Trans. Power Syst., vol. 27, no. 1, pp. 233–242, Feb. 2012, doi: 10.1109/TPWRS.2011.2168833. [13] P. K. Roy and S. Bhui, “Multi-objective quasi-oppositional teaching learning based optimization for economic emission load dispatch problem,” Int. J. Electr. Power Energy Syst., vol. 53, pp. 937–948, Dec. 2013, doi: 10.1016/j.ijepes.2013.06.015.

Copyright

Copyright © 2023 Ramamoorthi R, Balamurugan R. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.