Sudoku Solving Using Quantum Computer

Abstract

: We use ability of quantum computing such as superposition and entanglement to solve the sudoku. In recent years, quantum computers have shown promise as a new technology for solving complex problems in various fields, including optimization and cryptography. In this paper, we investigate the potential of quantum computers for solving Sudoku puzzles. We present a quantum algorithm for solving Sudoku puzzles, and compare its performance to classical algorithms. Our results show that the quantum algorithm outperforms classical algorithms in terms of both speed and accuracy, and provides a new tool for solving Sudoku puzzles efficiently. Additionally, we discuss the implications of our results for the development of quantum algorithms for solving other combinatorial problems.

Introduction

I. INTRODUCTION

Sudoku is a popular puzzle where one must arrange numbers such that no row, column, or block contains a number more than once. The most common variant of Sudoku consists of a 3x3 grid of 3x3 blocks, wherein every 3x3 block, rows, and columns must have the numbers between 1 and 9 including both exactly once, and where some of the numbers are revealed to facilitate finding the solution.There are couple of Sudoku problems which takes lesser time to solve. A sudoku problem is classically solved by trying all the possibilities in the empty spaces without violating its rules. The time complexity for such classical approach is O(p^q), where p denotes the count of empty positions and q denotes the total possibilities for a position which is 9 for 3x3 sudoku. Talking about quantum computing, the problem can be solved in miraculously O(log(n)) time complexity.

Sudoku is an important type of constraint satisfaction problems. Problem difficulty of sudoku comes with two main aspects. First being the complexity of individual steps which are independent and the second aspect being the figuring out of dependency with independent steps, i.e., in other words either steps are independent (can be applied parallelly) or are dependent (done sequentially) .

We are yet to design an alogrithm which can solve NxN sudoku deterministically.  In the present work, we propose to solve the simplest 4 x 4 Sudoku (also known as Shi Doku) using quantum computing and implement the concept of duality computing using a probabilistic approach[7]. Sudoku is a puzzle that was introduced over 40 years ago but reached its global popularity around 2005. It is not just a popular puzzle, but is also a common topic of researchers, among some mathematicians and computer scientists.

A partially completed n2 n2 grid of cells makes up a Sudoku puzzle. The objective is to fill in the empty cells in such a way that each row, column, and n-box (together, the Sudoku's groups) precisely includes the numbers 1 through n2.

A Sudoku is considered legitimate if just one possible solution exists. The most popular Sudoku variation has n = 3 and features a 9X9 grid. Backtracking search is a strategy for solving sudoku. Backtracking entails starting with a sub-solution at first, when that sub-solution doesn't lead to the right answer in the end, just going back and changing it. We'll approach our Sudoku in a same manner. Probabilistic approaches to solve sudoku. 1/9, if you’ve assigned digit labels randomly. None of the 9 digits has any special property relative to the others within the constraints of Sudoku, so each is equally likely to appear in the middle square.

II. QUANTUM COMPUTING

Quantum computing is process that compute by using the laws  of quantum mechanism which is very emerging technology that harness the power of quantum mechanics too solve problems which are knotty for classical computer. Like

Quantum computer break encryption standard that we use today by finding prime factors of large integer in just minutes instead of thousand of years it word take for a classical computer to do. We don’t need to worry, we have real quantum hardware today is not quite powerful enough to do that just yet. However technology is advancing faster then ever. The cell phone we have today are more powerful than the mainframe that we used to send people to the moon. Today, New hardware available to thousands of developers. Engineers are constantly working towards developing the world's most powerful quantum machines, to bring the benefits of quantum computing to everyone. These machines are entirely different from the classical computers that have been around for decades. Researcher believe that we will soon be entering an era of quantum advances where quantum computer will we used to accelerate classical computer, just like GPUs

A. Why Quantum Computers are Faster

Quantum computer uses special bits called qubits. Unlike classical computer which binary bits which can hold value from 0 to 1 which are like switches. This way of computing has serve us well, So well, in fact that almost that all modern computers work this way. However this approach doesn’t solve all the problem that we have today, problem that grow exponentially that would take a classical computer  decade to solve. Problems like encryption, optimization ,chemistry simulation .

While the qubit can 0 or 1 or any linear combination of the two. This spectrum of state is what we call a superposition.

A classical computer use bits 1 and 0  and arranges into core processor made up classical component process them using arithmetic and logical operation and gets an answer. In case of quantum computer we start with different definition of bits which are in super position of ones and zeros in other word it is sort of ones and zeros in parallel at same time

Let's see a example where quantum computers can succeed where classical computers fail: 

Despite the fact that a supercomputer is effective in difficult things such as sorting via a big database of protein sequences, it may not be as efficient at seeing the subtle patterns that decide how those proteins are behave.

Proteins are a sequence of amino acids that can fold into complex shapes in order to become correct biological machines. finding out exactly how proteins will retract is a problem with an   important significance for multiple fields.

A binary bits supercomputer might try to retract a protein using brute force, leveraging its many cpu to check on each way of turn the compound chain before  coming to a solution but since the protein sequences go longer and more advanced, the supercomputer stalls. a series of 100 amino acids can theoretically fold in a number of different ways, e. g. to create any one of thousands of different proteins. Even if you had the world 's most powerful computer, it has limited working memory and so would only be able to handle a few dozen or so configurations. Quantum computer finds new algorithm approach to these to sort complex problems by creating Multifaceted space where the patterns are linked from data points. A protein folding problem can often be solved by looking at the lowest energy possible; meaning you are going to want to look at all of the possible combinations that need the least energy. Classical computers cannot be replaced by Quantum computers but the problem of code-breaking  even cannot be solve by our most advanced supercomputers .It will take time almost equal to lifespan of our solar Systems . Qubits make it possible. Qubit is the superposition of 1 and 0 ,it don’t use the absolute value (complete value) 0 and 1.It is hybrid state(qubits don’t have values) of 0 and 1at once.In  traditional one computer if you have 4 bits you can hold one of the 16  traditional state(0000,0001,0010.......1111), but by having 4 Qubits can be in emplacement of 16 traditional states. Let take a easy example to make it more understand about qubits, if you have traditional one computer which uses 64-bits Intel Core i7 processor operates 3,20,00,00,000 operations/sec. hold any of 2 ^64 states at any instance. Even by having these specifications  it will take more than 100 years to evaluate 2^64 states . Quantum computer having sufficient qubits will process them at once because of superposition .IBM and Microsoft  are the two major companies which uses quantum computing(IBM’s Qiskit and Microsoft’s Q#).In qiskit we used python and Q# used.

In my quantum journey,  grover’s  algorithm is the most efficient searching algorithm .Grover’s algorithm works on unsorted or unstructured data. It finds high probability of finding the unique input using black box function. Using the Grover’s algorithms  ,we can find the input in less than O(n) ,also it will not provide polynomial time solutions for NP-complete problems.

III. GROVER'S ALGORITHM

In quantum computing, Grover's algorithm, also known as the quantum search algorithm, refers to a quantum algorithm for unstructured search that finds with high probability the unique input to a black box function that produces a particular output value, using just 0(\sqrt N) evaluations of the function, where 0(N) is the size of the function's domain. It was devised by Lov Grover in 1996 [1]. It is a quantum algorithm for finding the input value x* of a function f(x) with f(x*)=1 and f(x) for all value of x. A problem in classical computation can't be solved in the quickest possible fashion when the number of evaluations is linear, or O(N) (because half of the domain must be evaluated on average to find a 50% chance of it being correct).

Grover 's algorithmic rule is asymptotically optimal. Traditional solutions for NP- complete problems take a lot of time , but Grover 's algorithm can Offers maximum a quadratic fast solution over a classical solution for unstructured search. This is to say that Grover's algorithm will not solve NP-complete problems in polynomial-time(as the square root of an exponential function is an exponential, not polynomial, function)[5].

Grover’s algorithm implements amplitude amplification to increase the probability of observing the correct answer (the object of the search)

• Increases probability amplitude associated with answer |ket>
• Decreases all other probability amplitudes

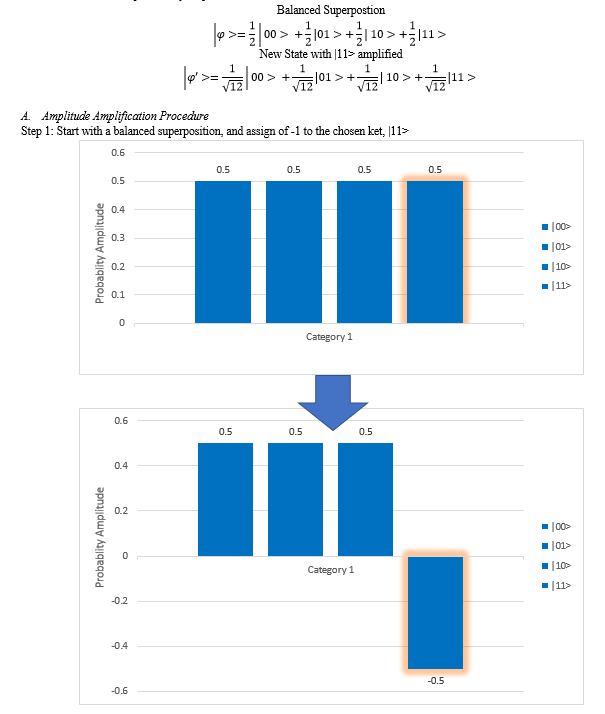
E. 2x2 sudoku

Qiskit’s Grover’s algorithm completes with the algorithm that solves sudoku of order 2x2. A valid solution can be reached without much efforts even without the concepts of quantum computing just that a number may appear only once in a row and column. It’s a great place to start and it is magnificent to evaluate sudoku of order 2x2 using quantum computing concepts, I am prompt to stretch this analysis to Sudokus of larger order.

Using Qiskit’s textbook wording: it may be difficult to find a solution to a regular 9x9 Sudoku but, given one, it is easy to verify that it is a valid one. The graph coloring problem (find the coloring of n nodes where pairs connected by vertices cannot have the same color) can also be formulated in these terms, and examples of that are found in Q# and Katas tutorials.[6]

My Quantum solver for Sudoku is based upon the Quantum tutorial on graph coloring using Grover’s search alogrithm and follow the plan on superpositions from Katas - challenges

A first step to solving a Sudoku is to convert the numbers into binary so a series of 0 and 1 can represent an easy-to-read solution.

F. Approach 1

Grovers algorithm helps us unstructured search problem so we convert it into search problem in best case  checking all the elements will eventually would rest in O(n), and it would make N/2 comparison.

However on quantum computer this type f problem can be solved in O(√N) times by the general ideas of Grover’s algorithm we need to amplify the amplitude of the solutions so we can measure it easily.

we have to initialized the system to have uniform distribution so as to have the same amplitude in every N state by This can we done by qubits register initialized in the state |0 >*N and applying Hadamard-gate over all qubits with H⊗n.

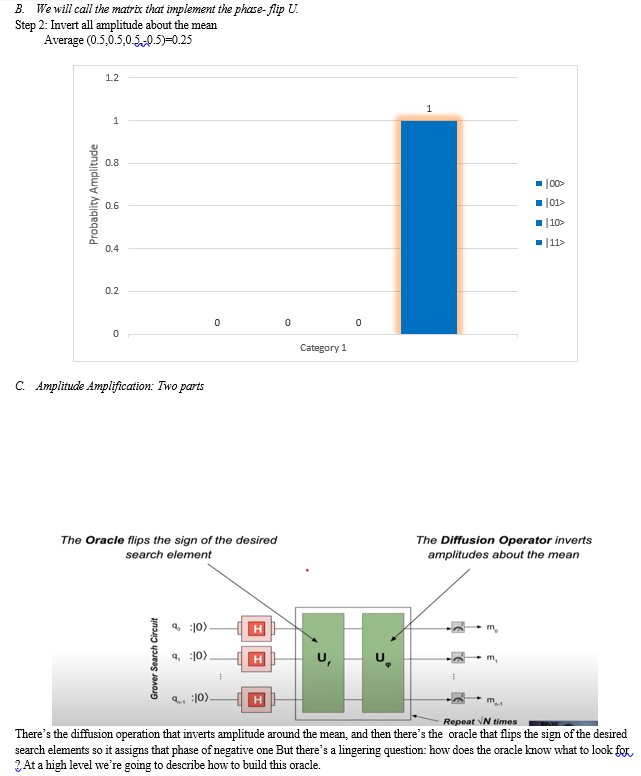
This lead to superpositions of state so due to this probability of getting correct answer world be 1/N, so we need to increase the amplitude of certain state, to did so we need to resign the diffuser. The effect of diffuser on states would be inversion about average in easy word we can say the oracle marks the solution  state with negative sign to encode the information  about the specific translating into a phase shift over system state  while the diffuser amplifies this marked state amplitude over all the others.

1. Steps

a. Initialization Application of of H⊗n to first n qubit and HX to last ancilla.

b. Oracle invert the aptitude of |x> that are solution

c. Diffuser amplifies those solution’s amplitudes by inverting them over the average of all the amplitudes

d. The measurement yields the solution, probability of solution is more than others.

2. Code

from qiskit import *

import numpy as np

from qiskit.providers.aer import QasmSimulator

from qiskit.visualization import plot_histogram

from operator import itemgetter

a_string = QuantumRegister(1, name='a string')

b_string = QuantumRegister(1, name='b string')

c_string = QuantumRegister(1, name='c string')

d_string = QuantumRegister(1, name='d string')

all_0_ancilla_ab = QuantumRegister(2, name='all 0  ancilla ab')

all_0_ancilla_cd = QuantumRegister(2, name='all 0  ancilla cd')

all_0_ancilla_ac = QuantumRegister(2, name='all 0  ancilla ac')

all_0_ancilla_bd = QuantumRegister(2, name='all 0  ancilla bd')

out = QuantumRegister(1,name='output')

classical = ClassicalRegister(4, name='measure')

qc = QuantumCircuit(a_string, b_string, c_string, d_string, all_0_ancilla_ab,

    all_0_ancilla_cd, all_0_ancilla_ac, all_0_ancilla_bd, out, classical)

#out in -

qc.x(out)

qc.h(out)

#superposition of input

qc.h(a_string[0])

qc.h(b_string[0])

qc.h(c_string[0])

qc.h(d_string[0])

qc.barrier()

def oracle(qc):

    # comparator ab

    qc.x(b_string[0])

    qc.mct([a_string[0], b_string[0]], all_0_ancilla_ab[0])

    qc.x(a_string[0])

    qc.x(b_string[0])

    qc.mct([a_string[0], b_string[0]], all_0_ancilla_ab[1])

    qc.x(a_string[0])

    qc.cnot(all_0_ancilla_ab[0], all_0_ancilla_ab[1])

    qc.barrier()

    # comparator ac

    qc.x(c_string[0])

    qc.mct([a_string[0], c_string[0]], all_0_ancilla_ac[0])

    qc.x(a_string[0])

    qc.x(c_string[0])

    qc.mct([a_string[0], c_string[0]], all_0_ancilla_ac[1])

    qc.x(a_string[0])

    qc.cnot(all_0_ancilla_ac[0], all_0_ancilla_ac[1])

    qc.barrier()

    # comparator cd

    qc.x(d_string[0])

    qc.mct([d_string[0], c_string[0]], all_0_ancilla_cd[0])

    qc.x(c_string[0])

    qc.x(d_string[0])

    qc.mct([d_string[0], c_string[0]], all_0_ancilla_cd[1])

    qc.x(c_string[0])

    qc.cnot(all_0_ancilla_cd[0], all_0_ancilla_cd[1])

    qc.barrier()

    # comparator bd

    qc.x(b_string[0])

    qc.mct([d_string[0], b_string[0]], all_0_ancilla_bd[0])

    qc.x(d_string[0])

    qc.x(b_string[0])

    qc.mct([d_string[0], b_string[0]], all_0_ancilla_bd[1])

    qc.x(d_string[0])

    qc.cnot(all_0_ancilla_bd[0], all_0_ancilla_bd[1])

    qc.barrier()

def diffuser(qc):

    qc.h(a_string[0])

    qc.h(b_string[0])

    qc.h(c_string[0])

    qc.h(d_string[0])

 qc.x(a_string[0])

    qc.x(b_string[0])

    qc.x(c_string[0])

    qc.x(d_string[0])

    qc.h(a_string[0])

    qc.mct([ b_string[0], c_string[0], d_string[0]], a_string[0])

    qc.h(a_string[0])

   qc.x(a_string[0])

    qc.x(b_string[0])

    qc.x(c_string[0])

    qc.x(d_string[0])

    qc.h(a_string[0])

    qc.h(b_string[0])

    qc.h(c_string[0])

    qc.h(d_string[0])

  qc.barrier()

#n is the number of iteration of Grover operator

n = 2

for i in range (n):

    oracle(qc)

    qc.mct([all_0_ancilla_ab[1], all_0_ancilla_ac[1],all_0_ancilla_cd[1],

        all_0_ancilla_bd[1]], out)

    qc.barrier()

    oracle(qc)

    diffuser(qc)

qc.measure(a_string[0],classical[0])

qc.measure(b_string[0],classical[1])

qc.measure(c_string[0],classical[2])

qc.measure(d_string[0],classical[3])

print(qc)

def print_sudoku(dict):

    list=[]

    for item in dict:

        for a in item:

            list.append(a)

        data=np.array(list)

        shape=(2,2)

        sudoku=data.reshape(shape)

        print(sudoku)

        print('\n')

        list.clear()

#start simulation

backend = QasmSimulator()

result = execute(qc, backend=backend, shots=1024).result()

answer = result.get_counts()

plot_histogram(answer).show()

#return N max values

res = dict(sorted(answer.items(), key=itemgetter(1), reverse=True)[:2])

#print the sudoku schemas

print('the solutions are:')

print_sudoku(res)

References

[1] Grover, Lov K. (1996-07-01). \"A fast quantum mechanical algorithm for database search\". Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing. STOC \'96. Philadelphia, Pennsylvania, USA: Association for Computing Machinery: 212–219. arXiv:quant-ph/9605043. Bibcode:1996quant.ph..5043G. doi:10.1145/237814.237866. ISBN 978-0-89791-785-8. S2CID 207198067. [2] towardsdatascience.com [3] C. .Lavor Grover’s Algorithm: Quantum Database Search at Instituto de Matem´atica e Estat´?stica [4] Marlan O. Scully and M. S. Zubairy, Quantum optical implementation of Grover\'s algorithm [5] Quantum and Blockchain for Computing Paradigms Vision and Advancements by Neha gupta [6] Get started in Quantum Computing | by Sergio Capape | Towards Data Science [7] A Pal, S Chandra, V Mongia, BK Behera, PK Panigrahi , Solving Sudoku game using quantum computation

Copyright

Copyright © 2023 Varun Singh, Varun Sharma, Vasu Bachchas . This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.