An Overview of Application of Fuzzy Planar Graph in Orbit Positioning for Satellite

Abstract

A graph is a convenient way of representing information involving relationship between objects. Now-a-days, Fuzzy graph plays the most important role in the research area due to its wide range of application. Fuzzy graph theory is of two subclasses, namely (i) Fuzzy multi-graph and (ii) Fuzzy planar graph. Fuzzy planar graph is a very important subclass of fuzzy graph. In this paper, the fuzzy planar graph is studied with its properties. Also in this paper, one of its application say, orbit positioning for satellites are discussed.

Introduction

I. INTRODUCTION

It is quite well known that graphs are simply models of relations. A graph is a convenient way of representing information involving relationship between objects. The objects are represented by vertices and relations by edges. When there is vagueness in the description of the objects or in its relationships or in both, it is natural that we need to design a 'Fuzzy Graph Model'. A graph is a symmetric binary relation on a nonempty set. Similarly, a fuzzy graph is a symmetric binary fuzzy relation on a fuzzy subset.

The concept of fuzzy sets and fuzzy relations was introduced by L.A.Zadeh in 1965[1] and further studied[2]. Later, it was Rosenfeld who considered fuzzy relations on fuzzy sets and developed the theory of fuzzy graphs in 1975. During the same time Fuzzy Graph Theory: A Survey byR.T.Yeh[4] and S.Y. Bang have also introduced various connectedness concepts in fuzzy graphs. Yeh and Bang’s[4] approach for the study of fuzzy graphs were motivated by its applicability to pattern classification and clustering analysis.

They worked more with the fuzzy matrix of a fuzzy graph. Techniques of fuzzy clustering analysis is also studied[4].  After the pioneering work of .Rosenfeld [3] and R.T.Yeh and S.Y. Bang [4] in 1975, where some basic fuzzy graph theoretic concepts and applications have been indicated, several authors have been finding deeper results, and fuzzy analogues of many other graph theoretic concepts.

Introducing the notion of fuzzychordal graphs, W. L.Craine [5] has obtained the fuzzy analogue of the characterizations of interval graphs. The notion of fuzzy graphs is generalized to fuzzy hyper graphs. Bhattacharya has extended the definitions of eccentricity and centre based on the metric in fuzzy graphs defined in [3]. A. Somasundaram and S. Somasundaram [7] introduced the concepts of domination and total domination in fuzzy graphs and determined the domination number for several classes of fuzzy graphs and obtained bounds for the same. A Somasundaram [6] studied several operations on fuzzy graphs such as union, join, composition, Cartesian product and obtained their domination parameters. The structural property of fuzzy finite graphs provided a tool that allowed for the solution of operations research problems. In the same paper the authors examined the properties of various types of fuzzy cycles, fuzzy trees, fuzzy bridges, and fuzzy cut nodes in fuzzy.

AssiaAlaoui extended the concepts of internal stability, external stability, external domination and some of their combinations to fuzzy graphs.

The concept of strong arc in maximum spanning trees [8] and its applications in cluster analysis and neural networks [9] were studied by Sameena and Sunitha. Geodetic distance (g-distance) in fuzzy trees, strong degree of a node and g-self centered fuzzy graphs were also studied by the same authors in [9]. Applications of fuzzy graphs to database theory, to problem concerning the group structure and also to chemical structures are found in literature.

A. Graph

A graph G = (V, E) is finite if V and E both are finite sets. An infinite graph is one with an infinite set of vertices or edges or both.

B. Fuzzy Graph

A fuzzy graph G = (V,s,m) is a non-empty set V together with a pair of function s=V ®[0,1] and m:V ´V®[0,1] such that all x, yÎV, m(x, y) £s(x) Ùs(y) where s(x) and m(x, y) represent the membership values of the vertex x and of the edge (x, y) in G respectively.

C. Fuzzy Planar Graph

If a fuzzy graph G can be drawn on a plane such that no two of its edges intersect than G is called fuzzy planar graph. Otherwise the fuzzy graph is non-planar fuzzy graph.

Example

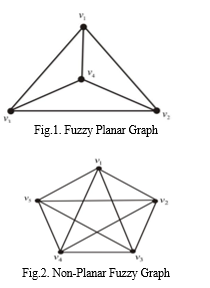
Here, the Fig2. is non-planar, since the edges in this graph intersects.

II. WHAT IS SATELLITE

A Satellite is a moon, planet or machine that orbits a planet or star. For example, Earth is a satellite because it orbits the sun. Likewise, the moon is a satellite because it orbits Earth. Usually, the word "satellite" refers to a machine that is launched into space and moves around Earth or another body in space. Satellite is an artificial object which is makes to rotate around the earth in order to collect the information and for communication. The satellite serves as a relay station between earth stations at different locations.

A satellite doesn't necessarily have to be a tin can spinning through space. The word "satellite" is more general than that: it means a smaller, space based object moving in a loop (an orbit) around a larger object. The Moon is a natural satellite of Earth, for example, because gravity locks it in orbit around our planet. The tin cans we think of as satellites are actually artificial (human-built) satellites that move in precisely calculated paths, circular or elliptical (oval), at various distances from Earth, usually well outside its atmosphere. In the context of spaceflight, a satellite is an artificial object which has been intentionally placed into orbit. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as Earth's Moon.

Satellites are specifically made for telecommunication purpose. They are used for mobile applications such as communication to ships, vehicles, planes, hand -held terminals and for TV and radio broadcasting. They are responsible for providing these services to an assigned region (area) on the earth. The power and bandwidth of these satellites depend upon the preferred size of the footprint, complexity of the traffic control protocol schemes and the cost of ground stations. A satellite works most efficiently when the transmissions are focused with a desired area. Satellites antenna patterns play an important role and must be designed to best cover the designated geographical area (which is generally irregular in shape). Satellites should be designed by keeping in mind its usability for short and long term effects throughout its life time.

A. Satellite Positioning

Within the last twenty years Global Positioning System (GPS) receivers have revolutionised navigation. Integrated devices are capable of providing time, position, height, direction, heave and attitude to accuracies of a few nanoseconds time, 1cm position or 0.01 degree heading. All potentially displayed on a digital chart background with radar and auto-identification system overlays. In this first we look at current Satellite Positioning systems, how they work and how we can make them better.

B. Satellite Navigation

Each Global Navigation Satellite System (GNSS) satellite transmits a number of carrier frequencies upon which are a number of codes. These include timing intervals, satellite positioning information, an ionosphere model and a code specific to the satellite, allowing multiple satellites to transmit on the same frequencies. Receivers may use some or all of these frequencies and codes and this will determine to a large extent the positioning performance.

The GNSS receiver has multiple receiver channels and generates its own internal version of the GNSS signal to compare against the signals received. The difference in time between these two can be converted to a pseudo range distance by using the speed of light. An ephemeris (set of satellite position information) stored in the receiver may then be used to determine initial receiver position by trilateration. We need three simultaneous pseudo ranges from different satellites geometrically well spaced to solve for latitude, longitude and height. The satellites have onboard atomic clocks synchronised via the system Master Control Station to a master atomic clock on the ground that contributes to the fundamental timing infrastructure of the planet. Synchronised atomic time standards are too expensive to put in typical satellite-receiver user equipment, so a fourth satellite pseudo range observable is required to calculate the receiver clock offset to the synchronised system atomic time.

C. Signal Variability

To get more accurate positioning we need to consider more variables, as shown in Figure 4.

Orbit is the difference between the broadcast position and the true position. The total electron content (TEC) is based upon solar activity which is related to time of day, position with respect to the geo-magnetic equator and where we are in the eleven-year solar cycle. We are currently approaching a solar-cycle minimum but TEC can still be high, especially at 15 degrees north and south of the geo-magnetic equator at 14:00 local time. TEC affects each frequency differently and slows down pseudo ranges but advances carrier phases by equal amounts. A ratio of dual-frequency GNSS measurements can be used to correct for TEC-induced effects. Alternatively, a position and time-based ionosphere model can be used for single-frequency receivers. This typically corrects for 40-60% of TEC. Ionosphere models use an altitude of 350-400kms and provide a regular grid of zenith TEC values which have to be converted to slant delays via an elevation look-angle mapping function.

III. SATELLITE PRECISE POSITIONING – NECESSITY

The original motivation for satellite navigation was for military applications. Satellite navigation allows precision in the delivery of weapons to targets, greatly increasing their lethality whilst reducing inadvertent casualties from mis-directed weapons. Satellite navigation also allows forces to be directed and to locate themselves more easily, reducing the fog of war.

Now a global navigation satellite system, such as Galileo, is used to determine users location and the location of other people or objects at any given moment. The range of application of satellite navigation in the future is enormous, including both the public and private sectors across numerous market segments such as science, transport, agriculture etc. The ability to supply satellite navigation signals is also the ability to deny their availability. The operator of a satellite navigation system potentially has the ability to degrade or eliminate satellite navigation services over any territory it desires.[14] Satellites are specifically made for telecommunication purpose. They are used for mobile applications such as communication to ships, vehicles, planes, hand -held terminals and for TV and radio broadcasting. Satellite’s antenna patterns play an important role and must be designed to best cover the designated geographical area (which is generally irregular in shape). Satellites should be designed by keeping in mind its usability for short and long term effects throughout its life time. Scientific research satellites provide meteorological information, land survey data (e.g. remote sensing), Amateur (HAM) Radio, and other different scientific research applications such as earth science, marine science, and atmospheric research.

IV. WHY ORBIT POSITIONING FOR SATELLITES IS IMPORTANT

Actually, when the position of satellite and its orbit is not properly fixed, then there may crash happen between two satellites.  In order for a satellite to go into orbit around the earth, it must have some forward motion.  When a satellite is launched, it is given both vertical and forward motion.  Forward motion produces inertia, which tends to keep the satellite moving in a straight line.  Gravity tends to pull the satellite towards the earth. The inertia of the satellite is equalized by the earth’s gravitational pull.  The satellite constantly changes its direction from a straight line to a curved line to rotate about the earth.

To say, NASA and other U.S. and international organizations keep track of satellites in space. Collisions are rare because when a satellite is launched, it is placed into an orbit designed to avoid other satellites. But orbits can change over time. And the chances of a crash increase as more and more satellites are launched into space. In February 2009, two communications satellites - one American and one Russian - collided in space. This, however, is believed to be the first time two man-made satellites have collided accidentally. This is the major reason, that is, the orbit positioning for satellites need to be properly fixed. For such a thing, a special kind of graph say planar graph is applied.  Specifically Fuzzy planar graph is used to determine the orbit positioning for satellites.

V. INTER- SATELLITE COMMUNICATION

The communication between the satellites is defined as the inter-satellite communication. This is possible by the inter-satellite links.

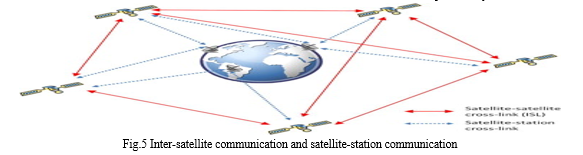
Inter-Satellite Links (ISLs) are intended to improve precision of orbit determination and satellite clock estimation. The ISLs provide a precise pseudorange measurements between satellites in a specific constellation.Inter-Satellite Links (ISLs) are considered to be a fundamental component of future Global Navigation Satellite Systems (GNSS) to improve the positioning accuracy and orbit determination. ISLs provide precise pseudorange measurements between satellites in a specific constellation. The combination of ISL and GNSS measurements is one of the key requirements for improving orbit determination.

Connections between satellites(Fig.6) can be used to transfer information, which might shorten the ephemeris update interval and improve navigation (Gong et al. 2019). One of the advantages of the ISL system is the potential to establish links outside of the atmosphere, and thus the ISL measurements are not affected by atmospheric delays and they are also less impacted by multipath and interference than GNSS measurements. It has also been suggested that satellites could determine their orbit autonomously by processing ISL measurements. Therefore, ISLs could make a great contribution to onboard processing and represent a step towards fully autonomous constellations in the future.

The concept of ISL exploitation was first proposed to support autonomous satellite navigation in Global Positioning System (GPS). It provided a possibility for satellites to self-navigate by using data exchanged with other satellites (Ananda et al. 1990; Huang et al. 2019; Sun et al. 2018; Tang et al. 2018; Xu et al. 2012; Zhou et al. 2018). GPS started introducing technology similar to ISLs in 1997 and used an ultra-high frequency (UHF) with Time Division Multiple Access (TDMA) scheme in Block IIR series. The current plans about the ISLs in next-generation GPS blocks are not publicly known.

At present, the BeiDou Navigation Satellite System (BDS) is the most advanced system to introduce ISLs. Since March 2015, new generation satellites have been launched to validate, among others, the ISL system. All in-orbit BDS-3 operational satellites are equipped with ISLs. The ISL payload enables observation of other satellites and ground stations with Ka-band single frequency pseudorange measurements. However, even with additional ISL measurements, the constellation is still affected by external environmental and technological effects. Observations to anchor stations, described as Ground-Satellite Links (GSLs), use the same communication and measurement system as ISLs.

VI. FUZZY PLANAR GRAPH REPRESENTATION OF SATELLITE COMMUNICATION

In the representation of the graph, the satellites are considered as the vertices and the path that connect the satellites are considered here as edges.

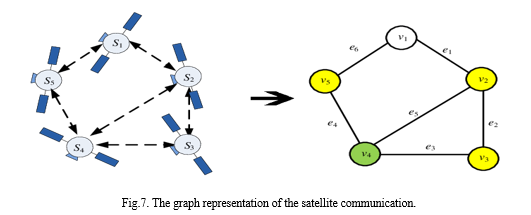
When inter-satellite communication is considered, it may be either planar or non-planar.

1. If it is planar then the satellite orbit positioning is fixed to the respective orbit.
2. If it is non-planar then the satellite orbit positioning is changed to another position and again it is checked either it is planar or non-planar. 

The inter satellite communication graph must be planar, because in non-planar graph the edges will intersect one another, which may leads to the miscommunication.  Thus, it is necessary to check whether the communication is planar or non-planar, before positioning the orbit for a satellite.

Conclusion

In this paper, we have discussed about the basics of fuzzy planar graph and satellite positioning. Also, in this study, we explored the possible behaviour of the estimation process based on GNSS observations combined with ISL measurements. However, Planarity is important in inter-satellite communication, which helps in the positioning of an orbit for the satellite. So fuzzy planar graph is an important topic for these positioning. In this paper, fuzzy planar graph for positioning the satellite’s orbit is described.

References

[1] L.A.Zadeh, Fuzzy sets, Information and Control, 8 (1965) 338-353. [2] L.A.Zadeh, toward a generalized theory of uncertainty (GTU)-an outline, Information Sciences, 172 (1-2) (2005) 1-40. [3] A.Rosenfeld, Fuzzy graphs, In: L.A.Zadeh, K.S.Fu and M.Shimura, Eds, Fuzzy Sets and their Applications, Academic Press, New York, (1975) 77- 95 [4] R.T.Yeh and S.Y.Bang, Fuzzy relations, fuzzy graphs and their applications to clustering analysis, In: L.A.Zadeh, K.S.Fu, M.Shimura, Eds, Fuzzy Sets and their Applications, Academic Press, (1975) 125-149 [5] W.L.Craine, Characterizations of fuzzy interval graphs, Fuzzy Sets and Systems, 68 (1994) 181-193. [6] A.Somasundaram, Domination in Fuzzy Graphs-II, Journal of Fuzzy Mathematics, 13 (2) (2005) 281-288. [7] A.Somasundaram, Domination in products of fuzzy graphs, International Journal of Uncertainity, Fuzziness and Knowledge Based Systems, 13(2) (2005) 195-204. [8] K.Sameena and M.S.Sunitha, Strong arcs and maximum spanning trees in fuzzy graphs, International Journal of Mathematical Sciences, 5(1) (2006) 17-20. [9] K.Sameena and M.S.Sunitha, On g-distance in fuzzy trees, International Journal of Mathematics and Systems, 19 ( 4) (2011) 787 – 791. [10] S. Samanta, M. Pal, and A. Pal, “New concept of fuzzy planar graph.” International Journal of Advanced Research in Artificial Intelligence, 3(1) (2014): 52-59. [11] Nirmala, G., and Prabavathi, S., “Mathematical Models in Terms of Balanced Signed Fuzzy Graphs with Generalized Modus Ponens Method.” International Journal of Science and Research (IJSR), 4(7) (2015): 2415-2419. [12] G. Nirmala and K. Dhanabal, “Special planar fuzzy graph configuration.” International Journal of Scientific and Research Publications, 2(7) (2012): 1-4. [13] C.Sujitha, “Connected fuzzy Planar Graph with Fuzzy if-then rule – A study.” Journal of Information and Computational Science (2019), ISSN: 1548-7741 [14] \"Applications\" www.gsa.europa.eu. 2011-08-18. Retrieved 2019-10-08 [15] M. Oliver and E. Gill, Satellite Orbits, Physics and Astronomy, May 2000. [16] R. Dach and S. Schaer, “Activities at the CODE analysis center,” in Proceedings of the IGS Workshop 2010 28, Newcastle upon Tyne, England, July 2010. [17] R. Dach, S. Lutz, M. Meindl, and G. Beutler, “Combining the observations from different GNSS,” in Proceedings of the European Geosciences Union General Assembly 2010, Vienna, Austria, May 2010. [18] B. Zhou and Y. Li, “Autonomous orbit determination for two spacecraft with measurement conversion,” in Proceedings of the 2019 Chinese Control Conference (CCC), pp. 4055–4059, IEEE, Guangzhou, China, July 2019. [19] B. Hou, D. Wang, T. Dong, J. Wang, and H. Zhou, “Monocular sequential images-based relative orbit determination method for near-range non-cooperative target,” in Proceedings of the 2020 International Symposium on Autonomous Systems (ISAS), pp. 201–206, IEEE, Guangzhou, China, December 2020. [20] Amarillo, F., Gerner, J.L., Lucas, R., et al. Inter-satellite ranging and inter-satellite communication links for enhancing satellite broadcast navigation data. In: 1st Colloquium in Scientific Applications of Galileo, Toulouse, 2007. [21] Fernández FA (2011) Inter-satellite ranging and inter-satellite communication links for enhancing GNSS satellite broadcast navigation data. Adv Sp Res 47:786–801. https://doi.org/10.1016/j.asr.2010.10.002 [22] Gong X, Huang D, Cai S, Zhou L, Yuan L, Feng W (2019) Parameter decomposition filter of BDS-3 combined orbit determination using inter-satellite link observations. Adv Sp Res 64:88–103. https://doi.org/10.1016/j.asr.2019.03.017

Copyright

Copyright © 2022 Naveen L, Uma N, Harsavarthini K R. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.