An Approch for Representation of Node Using Graph Transformer Networks

Abstract

In representation learning on graphs, graph neural networks (GNNs) have been widely employed and have attained cutting-edge performance in tasks like node categorization and link prediction. However, the majority of GNNs now in use are made to learn node representations on homogenous and fixed graphs. The limits are particularly significant when learning representations on a network that has been incorrectly described or one that is heterogeneous, or made up of different kinds of nodes and edges. This study proposes Graph Transformer Networks (GTNs), which may generate new network structures by finding valuable connections between disconnected nodes in the original graph and learning efficient node representation on the new graphs end-to-end. A basic layer of GTNs called the Graph Transformer layer learns a soft selection of edge types and composite relations to produce meaningful multi-hop connections known as meta-paths. This research demonstrates that GTNs can learn new graph structures from data and tasks without any prior domain expertise and that they can then use convolution on the new graphs to provide effective node representation. GTNs outperformed state-of-the-art approaches that need pre-defined meta-paths from domain knowledge in all three benchmark node classification tasks without the use of domain-specific graph pre-processing.

Introduction

I. INTRODUCTION

Deep networks can analyze structured inputs like molecules or social networks thanks to graph neural networks (GNNs). GNNs learn mappings from the structure and characteristics in their surroundings to calculate representations at graph nodes and/or edges. This local-neighborhood aggregation makes use of the relational inductive bias represented by the connectedness of the network [1]. By stacking layers, GNNs may gather data from outside of local neighborhoods similarly to convolutional neural networks (CNNs), hence expanding the GNN receptive field.

Since the creation of Transformers [2], which are now the top-performing neural network designs for handling long-term sequential datasets like sentences in NLP, there has been a huge amount of progress made in the field of natural language processing (NLP). This is accomplished through the employment of the attention mechanism [3], in which each word in a phrase pays attention to the words around it and integrates the information it receives to produce abstract feature representations. This technique of learning word feature representations by merging feature information from other words in a sentence may instead be considered as an instance of a GNN applied on a fully connected graph of words [5] from a message-passing paradigm [4] in graph neural networks (GNNs) viewpoint.

Graph Neural Networks (GNNs) have gained significant traction in recent years for a variety of graph-related tasks, including graph classification [22, 23, 24], link prediction [25, 26, 27], and node classification [28, 29, 30]. State-of-the-art performance in a range of graph datasets, including social networks [31,29,32], citation networks [33,30], the functional structure of brains [34], and recommender systems [35,36,37], has been demonstrated to be possible using the representation learned by GNNs. GNNs make use of the underlying graph structure to either execute convolution in the spectrum domain using the Fourier basis of a particular graph, i.e., the eigenfunctions of the Laplacian operator [38,3], or to operate convolution directly on graphs by passing node information [4,29] to neighbors.

However, a drawback of the majority of GNNs is that they presumptively function on fixed, homogenous graph structures. Since the fixed graph structure determines the previously stated graph convolutions, a noisy graph with missing or false connections yields an inefficient convolution with incorrect neighbors on the graph. Additionally, creating a graph to run GNNs is not always simple in some applications. For instance, a citation network is referred to as a heterogeneous graph because it has several node types (such as authors, papers, and conferences) and edges that are determined by the relationships between them (such as author-paper, and paper-conference). Neglecting the node/edge types and treating them as they are in a homogenous network is a naive approach (a standard graph with one type of node and edges).

This is not ideal because models cannot make use of the type of information. A more recent solution is to manually create meta-pathways, or paths joined by heterogeneous edges, and convert a heterogeneous network into a homogeneous graph that is defined by the meta-paths. The altered homogeneous graphs can then be used as input for standard GNNs [40, 41]. This strategy involves two stages and calls for individually created meta-paths for every issue. The selection of these meta-paths can have a big impact on how accurate downstream analysis is.

Modern performance on numerous NLP applications has been achieved using models based on transformers [6,7,8]. However, graph neural networks (GNNs) have shown to be the most successful neural network designs on graph datasets and have made substantial progress in a variety of fields, including physics [12,13], social sciences [11], and knowledge graphs [9,10]. In particular, GNNs take advantage of the flexible graph structure that is provided to learn the feature representations for the nodes and edges, and then they apply the learned representations to subsequent tasks.

For many computer vision tasks, such as object identification [14], picture classification [15], segmentation [16], facial recognition [17], and captioning [18], convolutional neural networks (CNNs) have become the de facto standard. The monkey visual system served as the inspiration for the inductive bias in CNNs, and the layer activations of these networks have been utilized to explain neural activations inside them [19]. Understanding the representations and techniques picked up by CNNs trained on well-known datasets like ImageNet has received a lot of attention recently [20,21]. Behavioral analysis analyzing model categories to learn more about the underlying representations—takes the form of much of this.

II. LITERATURE REVIEW

For a variety of purposes, several classes of GNNs have been created recently. They are divided into spectral [42] and non-spectral techniques [31] approaches. [42] suggested a method for performing spectral convolution in the spectrum domain by exploiting the Fourier basis of a certain graph, which is based on spectral graph theory. [33] convolution of the spectral graph with simplified GNNs of the first order. The definition of convolution operations, on the other hand, is done directly on the graph using spatially close neighbors in non-spectral techniques. Examples include [30]'s use of various weight matrices for nodes with various degrees and [29]'s learnable aggregator functions, which condense neighboring nodes' information for graph representation learning.

For many years, node categorization has been investigated. Traditionally, hand-crafted features like graph kernels, basic graph statistics, and engineering characteristics from a local neighbor structure have been utilized. These features lack flexibility and have subpar performance. Recently, node representation learning approaches using random walks on graphs have been suggested in Deep Walk [44], LINE [47], and node2vec [48], and have improved performance in part because of deep learning model tricks (such as skip-gram). All of these techniques, however, exclusively use the graph structure to learn node representation. The representations are not task-specifically optimized. GNNs learn a potent representation for the tasks and data they are given since CNNs have been so successful in representation learning. Generalized convolution based on spectral convolution [49, 50], attention mechanism on neighbors [51, 30], subsampling [43, 31], and inductive representation for a big network [29] have all been researched to enhance performance or scalability. Although these techniques produce excellent results, they are all constrained to work with homogeneous graphs.

But a lot of real-world issues frequently can't be modeled by a single homogenous graph. The graphs are delivered as heterogeneous graphs with a range of node and edge types. A two-stage method is one straightforward answer because most GNNs are made to work with a single homogenous graph. It pre-processes the heterogeneous graph into a homogeneous graph using meta-paths, which are the composite relations of various edge types and then learns representation. While HAN [40] learns graph representation learning by converting a heterogeneous graph into a homogeneous graph formed by meta-paths, the metapath2vec [51] learns graph representations by employing meta-path-based random walks. These methods, however, rely on manually chosen meta-paths made by subject matter experts, which means they might not be able to capture all significant linkages for each issue. Furthermore, the choice of meta-paths can have a big impact on performance. This Network Transformer network, in contrast to previous methods, can operate on a heterogeneous graph and transform it for tasks while learning end-to-end node representation on the altered graphs.

The over-smoothing issue is addressed by many suggested solutions using intermediate pooling processes resembling those in current CNNs. By typically condensing neighborhoods into a single node, graph pooling procedures continuously coarsen the graph in consecutive GNN layers [52, 53]. By removing unnecessary nodes and shortening the distance information must travel, hierarchical coarsening should, in principle, improve long-range learning. No graph pooling method, however, has been discovered to be as broadly applicable as CNN pooling. Modern results are frequently achieved using models that do not coarsen the intermediate graph [54], and some findings imply that neighborhood-local coarsening may be unnecessary or harmful [55]. This study mentions an alternative method for learning long-range dependencies in GNNs and pooling graphs.

This approach is similar to hierarchical pooling in that it substitutes purely learned operations like attention for some of the atomic operations that directly incorporate significant relational inductive biases (e.g., convolutions or spatial pooling in CNNs or neighborhood coarsening in GNNs) [56, 57].

III. METHODOLOGY

Our system, Graph Transformer Networks, is designed to concurrently create new graph structures and learn node representations on the learned graphs. Using several candidate adjacency matrices, GTNs search for novel graph topologies to execute more efficient graph convolutions and learn more potent node representations, in contrast to conventional CNNs on graphs that assume the graph is supplied. Finding meaningful multi-hop connections and meta-paths connected with different types of edges is a necessary step in learning new graph architectures. A brief review of the fundamental ideas of meta-paths and graph convolution in GCNs before proposing this methodology.

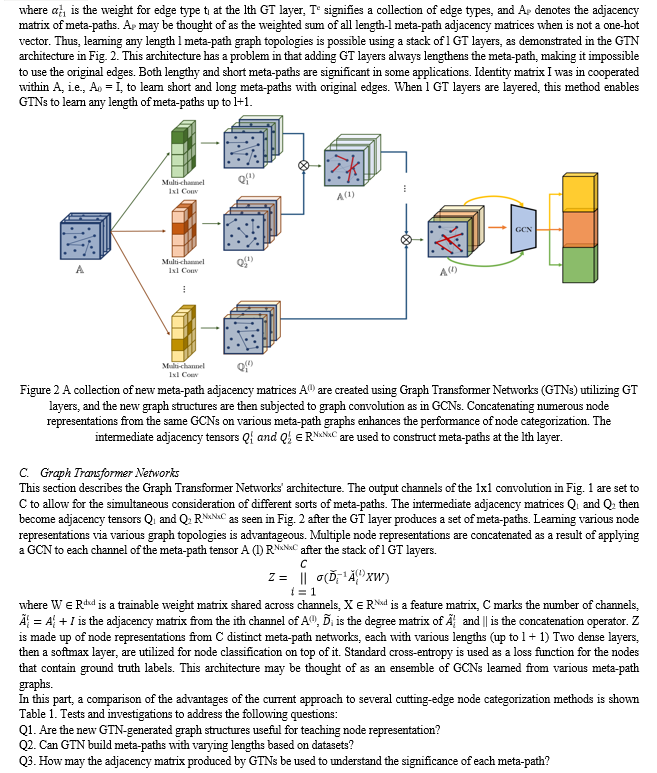
Conclusion

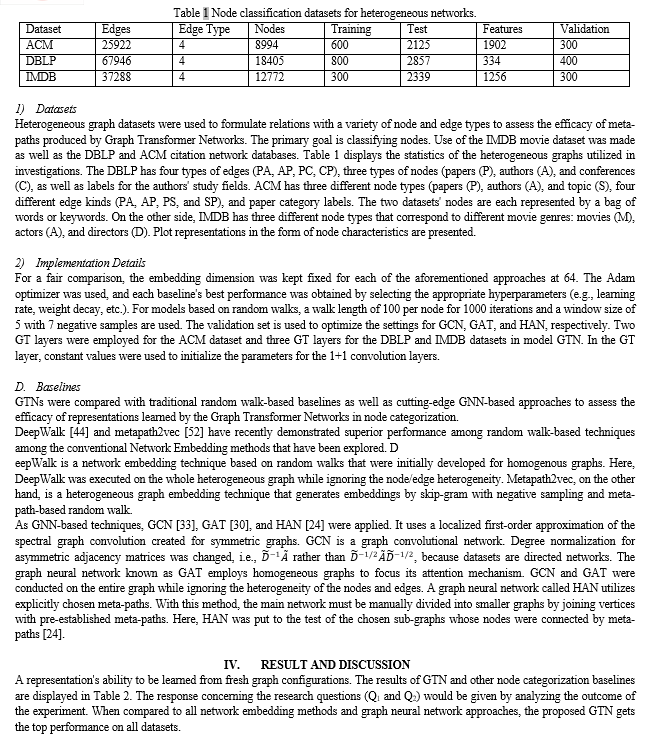
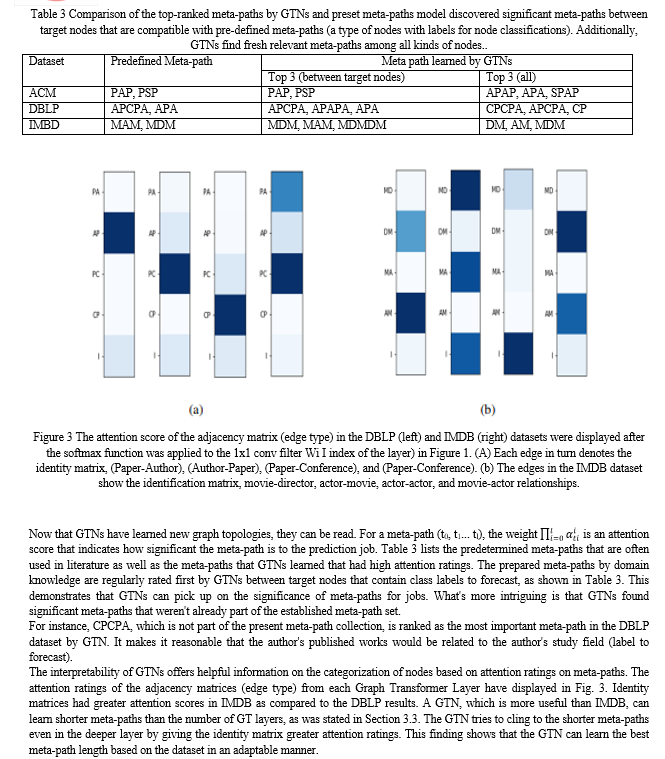
For learning node representation on a heterogeneous graph, this research introduced Graph Transformer Networks. This method learns node representation by convolution on the learned meta-path graphs while transforming a heterogeneous network into numerous new graphs defined by meta-paths with variable edge types and lengths up to one fewer than the number of Graph Transformer layers. With no specified meta-paths from domain knowledge, the learned graph topologies produce a state-of-the-art performance on all three benchmarks for node classification on heterogeneous networks. It’s observed that this framework creates new opportunities for GNNs to optimize graph structures on their own to operate convolution based on data and jobs without any human efforts since these Graph Transformer layers can be integrated with current GNNs. Future research should examine the effectiveness of GT layers paired with various kinds of GNNs rather than GCNs. Applying GTNs to the other tasks might be interesting future paths as well, since various heterogeneous graph datasets have recently been examined for other network research tasks, such as link prediction [61,62] and graph categorization [63, 64].

References

[1] P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez, V. Zambaldi, M. Malinowski, A. Tacchetti, D. Raposo, A. Santoro, R. Faulkner, C. Gulcehre, F. Song, A. Ballard, J. Gilmer, G. Dahl, A. Vaswani, K. Allen, C. Nash, V. Langston, C. Dyer, N. Heess, D. Wierstra, P. Kohli, M. Botvinick, O. Vinyals, Y. Li, and R. Pascanu. Relational inductive biases, deep learning, and graph networks. ArXiv preprint, abs/1806.01261, 2018. URL https://arxiv.org/abs/ 1806.01261. [2] Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A. N.; Kaiser, ?.; and Polosukhin, I. 2017. Attention is all you need. In Advances in neural information processing systems, 5998–6008. [3] Bahdanau, D.; Cho, K.; and Bengio, Y. 2014. Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473 . [4] Gilmer, J.; Schoenholz, S. S.; Riley, P. F.; Vinyals, O.; and Dahl, G. E. 2017. Neural message passing for quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning-Volume 70, 1263–1272. JMLR. org. [5] Joshi, C. 2020. Transformers are Graph Neural Networks. The Gradient . [6] Devlin, J.; Chang, M.-W.; Lee, K.; and Toutanova, K. 2018. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805 . [7] Radford, A.; Narasimhan, K.; Salimans, T.; and Sutskever, I. 2018. Improving language understanding by generative pre-training. [8] Brown, T. B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. 2020. Language models are few-shot learners. arXiv preprint arXiv:2005.14165 . [9] Schlichtkrull, M.; Kipf, T. N.; Bloem, P.; Van Den Berg, R.; Titov, I.; and Welling, M. 2018. Modeling relational data with graph convolutional networks. In European Semantic Web Conference, 593–607. Springer. [10] Chami, I.; Wolf, A.; Juan, D.-C.; Sala, F.; Ravi, S.; and Re,´ C. 2020. Low-Dimensional Hyperbolic Knowledge Graph Embeddings. arXiv preprint arXiv:2005.00545 . [11] Monti, F.; Frasca, F.; Eynard, D.; Mannion, D.; and Bronstein, M. M. 2019. Fake news detection on social media using geometric deep learning. arXiv preprint arXiv:1902.06673 . [12] Cranmer, M. D.; Xu, R.; Battaglia, P.; and Ho, S. 2019. Learning Symbolic Physics with Graph Networks. arXiv preprint arXiv:1909.05862 . [13] Sanchez-Gonzalez, A.; Godwin, J.; Pfaff, T.; Ying, R.; Leskovec, J.; and Battaglia, P. W. 2020. Learning to simulate complex physics with graph networks. arXiv preprint arXiv:2002.09405 . [14] Ren, S., He, K., Girshick, R., & Sun, J. (2015). Faster R-CNN: Towards real-time object detection with Region Rroposal Networks. In Advances in Neural Information Processing Systems (pp. 91–99). [15] Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems (pp. 1097–1105). [16] Girshick, R., Donahue, J., Darrell, T., & Malik, J. (2014). Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (pp. 580–587). [17] Schroff, F., Kalenichenko, D., & Philbin, J. (2015). FaceNet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (p. 815-823). [18] Chen, L., Zhang, H., Xiao, J., Nie, L., Shao, J., Liu, W., & Chua, T.-S. (2017). SCA-CNN: Spatial and channel-wise attention in convolutional networks for image captioning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (pp. 5659–5667). [19] Yamins, D. L. K., Hong, H., Cadieu, C. F., Solomon, E. A., Seibert, D., & DiCarlo, J. J. (2014). Performanceoptimized hierarchical models predict neural responses in higher visual cortex. Proceedings of the National Academy of Sciences, 111(23), 8619–8624. [20] Geirhos, R., Meding, K., & Wichmann, F. A. (2020). Beyond accuracy: Quantifying trial-by-trial behaviour of CNNs and humans by measuring error consistency. In Advances in Neural Information Processing Systems [21] Hermann, K., Chen, T., & Kornblith, S. (2020). The origins and prevalence of texture bias in convolutional neural networks. In Advances in Neural Information Processing Systems (pp. 19000–19015). [22] D. K. Duvenaud, D. Maclaurin, J. Iparraguirre, R. Bombarell, T. Hirzel, A. Aspuru-Guzik, and R. P. Adams. Convolutional networks on graphs for learning molecular fingerprints. In Advances in neural information processing systems, pages 2224–2232, 2015. [23] J. Lee, I. Lee, and J. Kang. Self-attention graph pooling. CoRR, 2019. [24] R. Ying, J. You, C. Morris, X. Ren, W. L. Hamilton, and J. Leskovec. Hierarchical graph representation learning with differentiable pooling. CoRR, abs/1806.08804, 2018. [25] T. N. Kipf and M. Welling. Variational graph auto-encoders. NIPS Workshop on Bayesian Deep Learning, 2016. [26] M. Schlichtkrull, T. N. Kipf, P. Bloem, R. Van Den Berg, I. Titov, and M. Welling. Modeling relational data with graph convolutional networks. In European Semantic Web Conference, pages 593–607, 2018. [31] C. Shi, Y. Li, J. Zhang, Y [27] M. Zhang and Y. Chen. Link prediction based on graph neural networks. In Advances in Neural Information Processing Systems, pages 5165–5175, 2018. [28] S. Bhagat, G. Cormode, and S. Muthukrishnan. Node classification in social networks. In Social network data analytics, pages 115–148. 2011. [29] W. L. Hamilton, R. Ying, and J. Leskovec. Inductive representation learning on large graphs. CoRR, abs/1706.02216, 2017. [30] P. Velickovi ? c, G. Cucurull, A. Casanova, A. Romero, P. Liò, and Y. Bengio. Graph attention ´ networks. In International Conference on Learning Representations, 2018. URL https: //openreview.net/forum?id=rJXMpikCZ. [31] J. Chen, T. Ma, and C. Xiao. FastGCN: Fast learning with graph convolutional networks via importance sampling. In International Conference on Learning Representations, 2018. [32] D. Wang, P. Cui, and W. Zhu. Structural deep network embedding. In Proceedings of the 22Nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 1225–1234, 2016. [33] T. N. Kipf and M. Welling. Semi-supervised classification with graph convolutional networks. In International Conference on Learning Representations (ICLR), 2017. [34] S. I. Ktena, S. Parisot, E. Ferrante, M. Rajchl, M. C. H. Lee, B. Glocker, and D. Rueckert. Distance metric learning using graph convolutional networks: Application to functional brain networks. CoRR, 2017. [35] R. v. d. Berg, T. N. Kipf, and M. Welling. Graph convolutional matrix completion. arXiv preprint arXiv:1706.02263, 2017. [36] F. Monti, M. Bronstein, and X. Bresson. Geometric matrix completion with recurrent multigraph neural networks. In Advances in Neural Information Processing Systems, pages 3697– 3707, 2017. [37] R. Ying, R. He, K. Chen, P. Eksombatchai, W. L. Hamilton, and J. Leskovec. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pages 974–983, 2018. [38] M. Defferrard, X. Bresson, and P. Vandergheynst. Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in neural information processing systems, pages 3844–3852, 2016. [39] M. Henaff, J. Bruna, and Y. LeCun. Deep convolutional networks on graph-structured data. CoRR, abs/1506.05163, 2015. [40] X. Wang, H. Ji, C. Shi, B. Wang, P. Cui, P. Yu, and Y. Ye. Heterogeneous graph attention network. CoRR, abs/1903.07293, 2019. [41] Y. Zhang, Y. Xiong, X. Kong, S. Li, J. Mi, and Y. Zhu. Deep collective classification in heterogeneous information networks. In Proceedings of the 2018 World Wide Web Conference on World Wide Web, pages 399–408, 2018. [42] J. Bruna, W. Zaremba, A. Szlam, and Y. LeCun. Spectral networks and locally connected networks on graphs. arXiv preprint arXiv:1312.6203, 2013. [43] J. Chen, J. Zhu, and L. Song. Stochastic training of graph convolutional networks with variance reduction. arXiv preprint arXiv:1710.10568, 2017. [44] B. Perozzi, R. Al-Rfou, and S. Skiena. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining, pages 701–710, 2014. [45] S. V. N. Vishwanathan, N. N. Schraudolph, R. Kondor, and K. M. Borgwardt. Graph kernels. Journal of Machine Learning Research, 11(Apr):1201–1242, 2010. [46] D. Liben-Nowell and J. Kleinberg. The link-prediction problem for social networks. Journal of the American society for information science and technology, 58(7):1019–1031, 2007. [47] J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan, and Q. Mei. Line: Large-scale information network embedding. In WWW, 2015. [48] A. Grover and J. Leskovec. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016. [49] M. M. Bronstein, J. Bruna, Y. LeCun, A. Szlam, and P. Vandergheynst. Geometric deep learning: going beyond euclidean data. IEEE Signal Processing Magazine, 34(4):18–42, 2017. [50] F. Monti, D. Boscaini, J. Masci, E. Rodolà, J. Svoboda, and M. M. Bronstein. Geometric deep learning on graphs and manifolds using mixture model cnns. CoRR, abs/1611.08402, 2016. [51] Z. Liu, C. Chen, L. Li, J. Zhou, X. Li, L. Song, and Y. Qi. Geniepath: Graph neural networks with adaptive receptive paths. arXiv preprint arXiv:1802.00910, 2018. [52] Y. Dong, N. V. Chawla, and A. Swami. metapath2vec: Scalable representation learning for heterogeneous networks. In KDD ’17, pages 135–144, 2017. [53] M. Defferrard, X. Bresson, and P. Vandergheynst. Convolutional neural networks on graphs with fast localized spectral filtering. In D. D. Lee, M. Sugiyama, U. von Luxburg, I. Guyon, and R. Garnett, editors, Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, December 5-10, 2016, Barcelona, Spain, pages 3837–3845, 2016. [54] Z. Ying, J. You, C. Morris, X. Ren, W. L. Hamilton, and J. Leskovec. Hierarchical graph representation learning with differentiable pooling. In S. Bengio, H. M. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett, editors, Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, December 3-8, 2018, Montréal, Canada, pages 4805–4815, 2018. [55] V. Thost and J. Chen. Directed acyclic graph neural networks. In 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, Austria, May 3-7, 2021. OpenReview.net, 2021. [56] D. P. P. Mesquita, A. H. S. Jr., and S. Kaski. Rethinking pooling in graph neural networks. In H. Larochelle, M. Ranzato, R. Hadsell, M. Balcan, and H. Lin, editors, Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual, 2020. [57] N. Carion, F. Massa, G. Synnaeve, N. Usunier, A. Kirillov, and S. Zagoruyko. End-to-End Object Detection with Transformers. ArXiv preprint, abs/2005.12872, 2020. [58] J. Cordonnier, A. Loukas, and M. Jaggi. On the relationship between self-attention and convolutional layers. In 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, April 26-30, 2020. OpenReview.net, 2020. [59] C. Shi, Y. Li, J. Zhang, Y. Sun, and S. Y. Philip. A survey of heterogeneous information network analysis. IEEE Transactions on Knowledge and Data Engineering, 29(1):17–37, 2016. [60] Y. Chen, Y. Kalantidis, J. Li, S. Yan, and J. Feng. A2-nets: Double attention networks. In ˆ Advances in Neural Information Processing Systems, pages 352–361, 2018. [61] X. Wang, X. He, Y. Cao, M. Liu, and T.-S. Chua. Kgat: Knowledge graph attention network for recommendation. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD), pages 950–958, 2019. [62] C. Zhang, D. Song, C. Huang, A. Swami, and N. V. Chawla. Heterogeneous graph neural network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD), pages 793–803, 2019. [63] H. Linmei, T. Yang, C. Shi, H. Ji, and X. Li. Heterogeneous graph attention networks for semi-supervised short text classification. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing (EMNLP), 2019. [64] R. Kim, C. H. So, M. Jeong, S. Lee, J. Kim, and J. Kang. Hats: A hierarchical graph attention

Copyright

Copyright © 2023 Dev Vaghani. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.