Design and Implementation of Area Efficient Low Latency Radix-8 Multiplier on FPGA

Abstract

Electronic systems are widely used by humans nowadays in all aspects of daily life. Today, there is no living for humans on Earth without any electronic products. High Speed, Low Power, and Low Area Electronic Systems are what the current generation needs. In digital systems, a variety of arithmetic circuits are employed. Adder, multiplier, divider, and other arithmetic circuits are some examples. To acquire Products from Multiplier and Multiplicand, there are various multipliers with various methods. One of the multipliers is Radix-4 Multiplier. The Radix-4 Multiplier produces n/2 partial products, where n is the multiplier\'s bit count. This multiplier has a high operating speed, power dissipation, and surface area. Area, power dissipation, and propagation delay can all be reduced by reducing the number of partial products of the n-bit multiplier. Radix-8 uses n-bit multiplier integers that are n/3 for partial products. The Area, Delay, and Power Dissipation are reduced as a result. 8-bit booth multipliers for Radix-4 and Radix-8 are designed and implemented using FPGA. For both multipliers, delay, power dissipation, and area are compared. According to the comparison, Radix8 Booth Multiplier performs better than Radix-4 Booth Multiplier in terms of delay, power dissipation, and area. Therefore, the Radix-4 Booth Multiplier can be swapped out for the Radix-8 Booth Multiplier.

Introduction

I. INTRODUCTION

Multipliers are crucial components of digital systems because their main purpose is to do multiplications. In classes like math, engineering, and IT, among others, they are given greater credit. Multiplication is crucial for the implementation of complicated algorithms, such as filtering, spectral alterations, helping, and multiplying, in the field of digital signal processing (DSP). Although binary multiplication is the simplest, many multipliers can effectively multiple in higher bases (radix 4, radix 8, etc.). Multipliers are essential for high-speed, reliable signal processing in applications based on very large scale integration (VLSI) and field programmable gate arrays (FPGA). There is a critical shortage of high-performance central processing units in the industrial sector. For many digital devices to operate more efficiently, mathematical operations like addition, multiplication, and subtraction are necessary. The effectiveness of the multiplication factor, the system's slowest component, determines the system rate as a whole. The multiplier uses a lot of energy and space, which reduces the system's total effectiveness. The exponent is used in deep learning, neural networks, digital computational signal-losing software, and a number of other applications. Our customers can choose from a wide range of power-saving algorithms and multipliers. The booth method uses a minimal amount of processing time, physical space, and energy. None of the algorithms for radices 2, 4, or 8 Booths can increase the effectiveness of digital multiples. These methods speed up computing because they reduce the number of additions that must be made. Using raw numbers represented as signed digits. The paper is organized in the following way: Section 1 has the introduction of the proposed model, Section 2 discusses the background and literature survey. Section 3 shows results of the proposed models with respective figures. Section 4 briefly discusses the conclusion and future scope of this paper.

II. Background and Literature survey

A. The Radix-2 Booth Algorithm

It uses the multiplier's corresponding bits to perform operations. When adjacent bits are different from one another, partial products are produced, but not when they are identical. Radix-2 appears straightforward, yet it can nevertheless produce significant partial results.

B. The Radix-4 Booth Algorithm

It uses bit pairs to produce negative, positive, or zero partial companies based on the values of the bit pairs, which further reduces partial products. Radix-4 increases the efficiency of multiplication by simultaneously examining two bits.

C. Radix-8 Booth Algorithm

To outperform the radix-4 approach, the radix-8 method examines three bits at once. It produces product components in a manner similar to radix-4, which might result in fewer products overall.

Systems built on VLSI and FPGA extensively rely on these Booth approaches, particularly in the field of digital signal processing (DSP). They speed up and save resources during multiplication by making use of regularities in the multiplier's bits representation. When choosing an effective algorithm, the trade-off between algorithm complexity and processing speed is a crucial factor. When these multipliers are used in an FPGA, the operations involved in digital signal processing are improved by finding a compromise between speed and complexity. and the use of resources. On an FPGA, the results of designing and implementing booth amplifiers for Radix-4 through Radix-8 were seen. Verilog HDL is used in the procedure. We started off with the NEXYS Artix 7 FPGA board.

The booth algorithm was first introduced by Andrew Donald Booth in 1950 in London. This algorithm served as a theoretical computer science exercise. This booth method adds two signed binary digits together in 2's complement form. This technique was created through research on crystals. The booth algorithm seems to have less additions and subtractions. The Booth multiplier is unmatched in terms of speed. This booth method is often used in ASIC devices due to its high computational speed and minimal memory requirements.

The booth algorithm's key steps are:

• Producing the incomplete products
• Cutting back on partial items
• Totalizing the partial pro

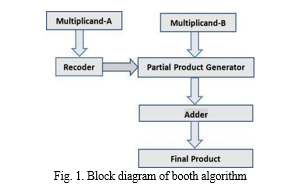
1. Encoder

The digital block encoder reverses the role of a decoder. It takes in 2n inputs and outputs n. In this booth process, the source of my encoder served as the multiplicand, and the encoder's input ultimately went to the partial result generator. A signal with a value proportional to its binary representation is generated by the encoder.

2. Partial Product Generator

Reducing the difficulty of computing the products of two or more numbers is the primary objective of the partial solution generator. For a given vector of zeros and ones, we can create the partial products in this case. The partial product reduction reduces the time needed to sum up partial products.

3. Adder

The partial products' production and reduction are followed by their summarization. Either the carry save adder or the carry look-ahead adder might be used to achieve this. Among the options are parallel prefix spikes like kogge stone adders, compressor adders, carry select adders, Wallace tree adders, and many others. We can reduce the delay parameter by choosing the right adder.

4. Final Product

It is possible to consider the inputs multiplicand A and multiplicand B as two signed binary numbers. the result will be the 2's complement number multiplied.

5. Limitations of Booth’s Algorithm

There is still work to be done on signed multiplication by one. The expense of overhead might not be necessary for enterprises with low volume. Booth's approach and the Booth encoding table are helpful whenever speed and hardware implementation are important, such as in digital signal processing, chip architecture, and computer arithmetic.

6. Radix-4 Booth Multiplier

Radix-4 Booth recoding can reduce the overall number of incomplete products by half. Instead of shifting + adding for each column and then multiplying by 1 or 0, the crucial strategy is to take every other column of the repeater term and multiply it by 1, 2, or 0. Using a radix-4 booth encoder, the multiplicand is encoded using the multiplier bits. It will compare three bits at once using an overlapping technique. The grouping starts with the least significant bit, and the first block only uses two of the multiplier's bits before assuming the third one is zero. The operational characteristics of the Radix-4 booth encoder are shown in the Table. There are eight unique stages, and each one leads to one of three outcomes: the multiplicand is multiplied by 0, 1, or 2. This article presents the Booth method for radix 4.

To make sure that n is even, if necessary, extend the sign bit 1 place. Add a 0 to the right of the plier's LSB. Each Partial Product will be 0, +1, -1, +2 or -2 depending on the value of each vector. The 2's complement produces y values that are negative. The 2's complement operation enables the production of negative values of y in the Carry-Select-Adder (CSA) rapid spikes used in this study. We can multiply y by a large number of factors by shifting it to the left by one bit. As a result, while creating n-bit parallel multipliers, only n/2 partial items are created (Hsin-Lei Lin 2004, H. Lee 2002, M. Sheplie 2004).One advantage of this strategy is the reduction in the number of intermediate products by half. This matters when designing circuits since it has an impact on the complexity, electricity consumption, and propagation of the circuit during operation. the delay of the circuits' introduction.

The binary numbers being multiplied in a radix-4 multiplier are divided into groups of four bits each, which can represent decimal values ranging from 0 to 15. The number of steps needed for the multiplication is then greatly decreased by processing these four-bit groups concurrently. The main concept is to take advantage of the fact that the base-4 system's digits (0, 1, 2, 3) may each be represented by just two bits in binary (00, 01, 10, and 11). As a result, the radix-4 multiplier can complete several additions in a single operation.

In comparison to conventional radix-2 multipliers, radix-4 multipliers are significantly faster and more hardware-efficient since they require less computations for partial products and adds. This qualifies them for uses where multiplication is a crucial function, such as in algorithms for digital signal processing, arithmetic units in microprocessors, and  many high-speed computing tasks .Radix-4 multipliers are faster than other techniques of multiplication, but it's important to keep in mind that they could also demand more sophisticated hardware and use more energy. Their choice of implementation therefore depends on the particular system requirements, such as the demand for speed, area efficiency, and power.

Table 1.  Radix-4 Booth Multiplier encoding

7. Carry Select Adder

A carry-select adder is often made up of a ripple-carry adder and a multiplexing device. In order to combine two n-bit values, a carry-select adder employs two additives (and therefore, two ripple-carry adders), one anticipating that the carry-in will be zero and once anticipating that it will be one.

The multiplexing function can be used to select the right total and carry-out from the two results once the suitable carry-in has been established. In key arithmetic circuits, such as processors and digital signal processors (DSPs), where quick arithmetic operations are crucial, this architecture enables CSA to dramatically increase the speed of addition.

The carry and sum bits are chosen by the carry-in in the carry-select adder shown above, which is built from two 4-bit ripple-carry adders that are multiplexed together. The intended outcome is obtained by identifying which ripple-carry adder has the correct hypothesis via the actual carry-in given two ripple-carry adders, one of which expects a carry-in of 0, and the opposite of which assumes a carry-in of 1.

8. Carry Select Adder's Benefits Include

Carry Select Adders are able to surpass more conventional ripple carry adders in terms of performance by utilising duality in carry production and propagation. By simply adding more groups, the Extend Select Adder's size may be increased to provide higher-bit addition with improved speed. The parallelization of carry generating and sum computing results in CSA's shorter critical path, which is the third factor enhancing speed.

9. Radix-4 Booth Multiplier Drawbacks Include

The 8-bit Radix-4 Terminal Multiplier is a quick, large-area, and high-power device.

10. Booth Multiplier for Radix-8

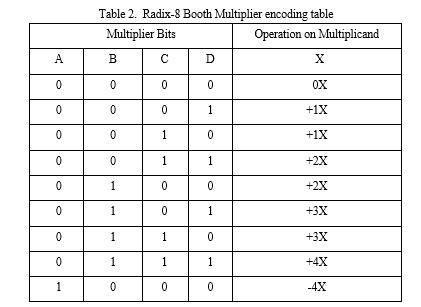
This approach is somewhat similar to Radix-4's in that it examines values of quartets rather than triplets. This strategy minimises the number of incomplete results to n/3 as opposed to Radix-4, which reduces it to n/2. Computing time and resources can be saved by lowering the required number of Partial Products. The booth encoding table for the Radix-booth re-coding Multiplier is shown in Table 2. Encoding table for the Radix-8 Booth multiplier. We can avoid these problems by switching to the Radix-8 Booth multiplier.

When base-8 encoding data, a radix-8 encoder table is used to convert groups of input symbols (usually binary) into radix-8 symbols in accordance with specified criteria. It makes the process of transforming data into a smaller, more effective representation for use in a variety of digital communication and coding theory applications simpler. A representation used in digital communication and coding is the radix-8 encoder table. Three-binary input symbol groups are translated into matching radix-8 (octal) symbols ranging from 0 to 7. For effective data conversion, the encoding rules are specified in each row of the table. Data compression, error-correcting coding, and digital communication applications are all aided by this table's simplified encoding procedures.

Conclusion

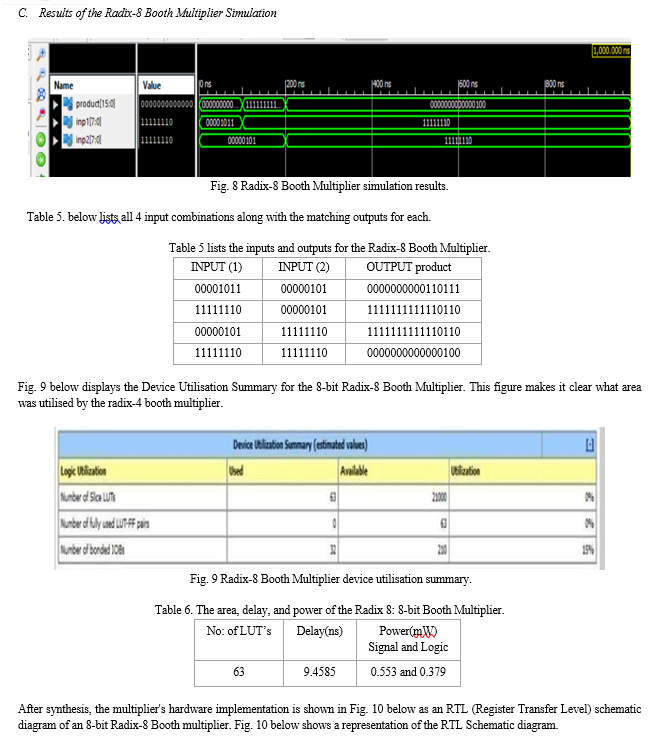
According to the literature survey, the n-bit Radix-4 converter has issues with large area utilisation, high power dissipation, and delay, mostly because of its n/2 full products. Booth multipliers with radix-4 and radix-8 were meticulously modelled, simulated, synthesised, and tested on an FPGA to overcome these problems. When the two were put side by side, the Radix-8 Booth Multiplier performed better in terms of area, latency, and power efficiency, providing a strong option. Its reliable operation was further confirmed by the modelling and testing findings. The project\'s successful conclusion may be facilitated by this switch from Radix-4 to Radix-8 Booth Multipliers by enabling high-speed, low-power, and space-efficient electronic devices. The following are the further enhancement that can be done for 8-bit Radix-8 Booth Multiplier: 1) The size of the Multiplier can be increased to 16,32,64-bits etc. 2) Speed can be improved by using some adders that have high speed

References

[1] Xilinx. 2018. 7 Series DSP48E1 Slice, UG479. [2] S. Ullah, et al., “Area-optimized low-latency approximate multipliers for FPGA-based hardware accelerators,” in DAC 2018. [3] I. Kuon et al., “Measuring the gap between FPGAs and ASICs,” in IEEE TCADICS 2007. [4] Xilinx. 2015. LogiCORE IP Multiplier v12.0, PG108. [5] A. D. Booth, “A Signed Binary Multiplication Technique,” in the Quarterly Journal of Mechanics and Applied Mathematics 1951. [6] C. R. Baugh et al., “A two’s complement parallel array multiplication algorithm,” in IEEE TC, vol. 100, no. 12, 1973. [7] M. Kumm, et al., “An efficientsoftcore multiplier architecture for Xilinx FPGAs,” in Computer Arithmetic (ARITH), 2015. [8] E. G. Walters, “Array Multipliers for High Throughput in Xilinx FPGAs with 6-Input LUTs,” in Computers, MDPI, 2016. [9] H. Parandeh-Afshar et al., “Measuring and reducing the performance gap between embedded and soft multipliers on FPGAs,“ in FPL, 2011. [10] Xilinx. 2016. 7 Series FPGAs Configurable Logic Block, UG474. [11] H. Parandeh-Afshar, et al., “Exploiting fast carry-chains of FPGAs for designing compressor trees,“ in FPL, 2009. [12] A. Kakacak et al., “Fast multiplier generator for FPGAs with LUT based partial product generation and column/row compression,” in Integr. VLSI J. 2017. [13] M. Kummet al., “Resource Optimal Design of Large Multipliers for FPGAs,” in ARITH 2017. [14] V. Mrazek et al., “Evoapprox8b: Library of approximate adders and multipliers for circuit design and benchmarking of approximation methods,” in DATE 2017. [15] G. W. Bewick, “Fast Multiplication: Algorithms and Implementation,” Dissertation, Stanford University, 1994. [16] V.Nagamani,“temperature and humidity sensor based air blower controller for food drying”journal of algebraic statistics volume 13, no. 1, 2022, p. 869 - 876 https://publishoa.com issn: 1309-3452 [17] “Integrated Optical Receiver Implementation using CMOS Technology” Journal of Emerging Technologies and Innovative Research, Vol5,issue 10, pp-953-957,Oct 2018. [18] Y.MallikarjunaRao, M.V.Subramanyam and K. Satyaprasad, “An efficient resource management algorithms for mobility management in wireless mesh networks”, IEEE Conference on energy, communication, data analytics and soft computing, SKR Engineering College, Chennai, 2017. [19] Y.MallikarjunaRao, M.V.Subramanyam and K. Satyaprasad, “Performance analysis of energy aware QoS enabled routing protocol for wireless mesh networks”, International journal of smart grid and green communications [20] Y.MallikarjunaRao et.al “Design and Performance Analysis of Buffer Inserted On-Chip Global Nano Interconnects in VSDM Technologies”, Nanotechnology for Environmental Engineering, 11 May, 2022, Springer.

Copyright

Copyright © 2023 Sumaya Sadaf, V. Radha Krishna. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.