A High-Performance On-Chip Memory Module for Image Processing Applications

Abstract

To actualize numerous image processing applications, today\'s technology revolution in portable electronic devices necessitates significant amounts of data processing power, area, and time. Approximate data computing has been demonstrated to be a viable solution for picture processing. In real-time digital data computing applications, achieving high precision or fulfilling a variable accuracy requirement of up to 100 percent has become a crucial design goal. As a result, very large-scale integration (VLSI) architectures with excellent performance are critical in the design of digital signal processors. The use of high-performance adders and on-chip memory structures has also been a focus of recent breakthroughs in processor design Stability and dependability are crucial design factors that contribute to a reduction in worst-case error and the use of a hybrid application in real time. High precision, high speed, low power, and area efficiency are achieved by balancing the restrictions of high performance. The processor core\'s performance is determined by the configuration, design parameters, and efficient use of the data channel and on-chip memory structures. As a result, high-performance adders and on-chip memory architecture were used in this study. To provide superior quantitative computation for human perception, the suggested design is included into image processing applications such as image approximation, canny edge detection, and noise reduction approaches. Berkeley, medical, and satellite image samples were used..

Introduction

I. INTRODUCTION

A. VLSI Design

We offer an overview of high-performance Very Large-Scale Integration (VLSI) architectures for image enhancement, as well as the core concepts, principles, and aspects of high-performance design approach, as well as the research study's rationale. To achieve high precision, fast speed, low power, and space efficiency, the restrictions associated in the high-performance design are counterbalanced. This also includes an overview of the design space exploration of high-performance VLSI domain with special reference to adder and on-chip modules, as well as the discovery of issue definition and research effort scope..

B. Need for High Performance Design

High-speed circuits expend a considerable quantity of energy in a short period of time with a rise in chip heating due to the enormous integration of functional devices on a single chip. When the chip is functioning at a high temperature, serious functional concerns develop. As the number of portable electronic devices grows, so does the number of operating system programmes that can be powered by the battery's small size. Low power operation in VLSI circuits is desirable to improve battery life and decrease increasing temperature. Complementary Metal Oxide Semiconductor is a major component of the VLSI chip (CMOS). As shown in Equations (1.1) to (1.2), the overall power consumption of a CMOS circuit contains both dynamic and static power components (1.5).

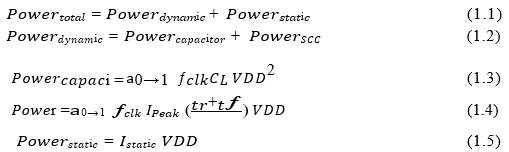
Where, in Equation (1.2), Powercapacitor denotes the dynamic power generated by the capacitance charging and discharging of a load capacitance. CL, a01 is the switching activity factor for a one-clock-period transition probability from logic "0" to logic "1," clk is the operating frequency, and VDD is the supply voltage.

PowerSCC is the power consumption due to short circuit peak current (IPeak) and is proportional to the CMOS transistor size. The limitations of time

The rise and fall times of short circuit current are represented by tr and t, accordingly.

The static power in Equation (1.5) is determined by the leakage current, which can be either reverse-biased PN junction current or sub-threshold current. From the lowest technology CMOS transistor level to the highest technology architectural levels, power optimization approaches have been investigated, influencing all parameters such as a01, CL, clk, and VDD while maintaining the needed function..

Because of the rising degrees of integration and the requirement for mobility, minimising the power consumption of circuits is vital for a broad variety of high-volume digital data computing applications. Because the speed of arithmetic components is frequently a limiting factor in performance, it is equally critical to increase that speed. At every design level, such as gate and transistor-level technologies, where the majority of the power may be avoided at the high conceptualization, power reduction must be addressed. An optimised compact design is sought at the gate level of high-performance architectures to provide energy efficiency, high speed, and reliability for large-quantity digital data computing applications. It's also crucial to have good driving abilities under various load levels and a balanced output to avoid errors. Layout regularity and connection complexity are critical since the modules are repeated in huge numbers. Optimizing the gate count for a certain performance is the greatest technique to minimise junction capacitance as well as overall gate capacitance. A number of optimization strategies have been developed to reduce the design area while preserving performance. Path optimization and global optimization are two types of design optimization. In path-based optimization, the critical routes' gates are increased in size to achieve the required performance, while the off-critical paths' gates count is lowered to achieve low power consumption..

All gates in an architecture are globally optimised for a specified delay in the global optimization. To meet the total system cycle time requirements, the designs are primarily built for maximum performance. They are made up of huge, highly parallel structures that follow a logic pattern. As a result, the leakage power consumption of such systems is significant. However, not every application need a fast circuit to run at peak speed all of the time. Using the timing slack, many circuit approaches have been developed to decrease leakage energy without compromising performance. These methods may be classified according on when and how they employ the available time slack. In non-critical logic gates, dual threshold voltage statically assigns high threshold voltage to certain transistors. The strategies that take advantage of the slack in runtime may be classified into two categories based on whether they minimise standby leakage or active leakage. When the calculation is not required, standby leakage reduction techniques can place the entire system into a low leakage state. When maximum performance is not required, active leakage reduction approaches slow down the system by dynamically altering the threshold voltage to decrease leakage. The operational temperature rises in active mode due to the switching actions of transistors. This has an exponential impact on sub-threshold leakage, multiplying the leakage power and making it the major leakage factor during active mode..

The space, speed, power dissipation, and wiring complexity of a chip level VLSI system are all influenced by the logic gates optimization and switching activity along the critical route.

II. OBJECTIVES OF THE RESEARCH

The following is a description of the research project's goal:

1. To build efficient adders to satisfy quality metrics necessary for high volume digital data approximation computing image processing applications by developing energy efficient, high speed, and area efficient Approximate Full Adder Logic (AFAL).
2. Develop and build reconfigurable adders to fulfil a varied accuracy need in the implementation of real-time exact, inexact, or hybrid applications, from worst case to best case (100 percent).
3. To provide a high-performance On-Chip memory module for image processing applications that are error-tolerant.

III. LITERATURE REVIEW

In the construction of an arithmetic module, adders are one of the most important components. The critical path delay in this architecture is likewise affected by the propagated signal's delay component and the adders' respective sizes. In the adder architecture, carry propagation is critical for achieving fast calculation speeds. A single bit full adder's carry propagation delay increases the total delay component in a multiple bits Ripple Carry Adder (RCA). As a result, the Carry Select Adder (CSLA) and Carry Look ahead Adder (CLA) structures were developed to minimise the carry propagation delay at the expense of space and energy.. For portable digital signal processing applications such as video, audio, and image processing, high speed, compact size, and energy efficiency might be accomplished at the expense of accuracy in high volume digital data calculation.

As a result, approximations have been performed in adders at various levels, which have been classified as segmented (Irina & Lau 2017; Kim & Kim 2016), reconfigurable (Andrew & Seokhyeong 2012; Garg et al. 2016), speculative (Ing et al. 2015; Junjun & Weikang 2015), floating addition (Rui & Weikang 2015; Weiqiang et all

(Haider et al. 2016), gate level (Ramkumar & Harish 2012), evolutionary type (Adnan et al. 2015; Radek et al. 2016), application specific adders (Darjn et al. 2016), carry truncation (Vincent et al. 2016), reversible logics (Pawan et al. 2015), and architectural level (Ning et al. 2010). Recent studies suggest that applications like probabilistic analytics, image, video, and machine learning applications, among others, have a high degree of error resilience (Sunil et al. 2016). For human vision, this allows for approximation computing rather than precise calculation (Melvin & Haiyang 2006). As a result, the key challenge for designers of approximation full adder designs is to achieve high accuracy, fast speed, low energy consumption, and area efficiency.

IV. METHODOLOGY

A. Proposed Approximate Full Adder Logic

Approximate full adder logic outperforms the existing Conventional Full Adder (CFA) in terms of speed, area, and energy efficiency (Mahdiani et al. 2010). A low-performance design could accept or tolerate probable mistakes to an acceptable degree. A high-performance architecture, on the other hand, can speculatively execute the approximate result rather than waiting for the exact result to become available. The speedup in machine cycles of an approximation unit relative to an exact unit is more sensitive to accuracy than throughput performance. As a result, four approximation full adder logics are provided for increasing the approximate arithmetic units' performance.

1. Approximate Full Adder AFSL

SUM = CARRY is used to create a simpleAFAL1 from an existing CFA. Table 1 shows the erroneous output as well as the error distances. Table 1 displays the AFAL1 function, which has two mistakes in the sum output and none in the carry output when all input bits are either "000"s or "111"s; otherwise, the sum and carry outputs are error-free..

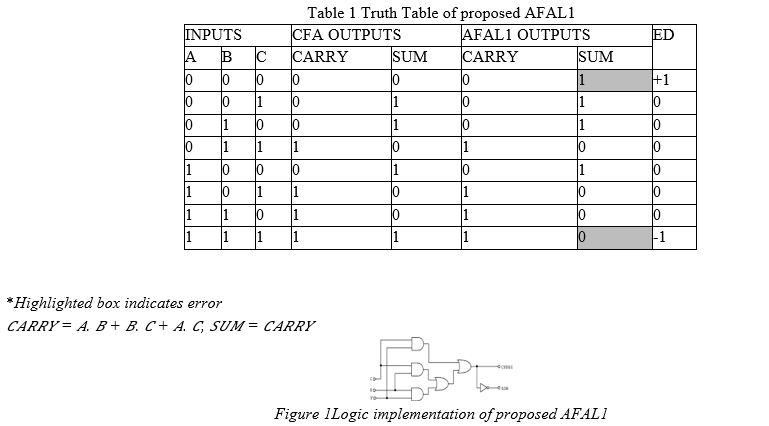
Figure 1 shows that AFAL1 has 6 basic logic gates (AND, OR, and NOT gates) and 4 logic delays instead of 13 basic logic gates (2*5) + 3 and 6 logic delays utilised by CFA to build the primary gate level structure (2 Exor gates (2*5) + 3). The principal inputs are "A" and "B," while "C" is the propagating input from the previous stage. The complement of the carry propagating signal output is the sum output.

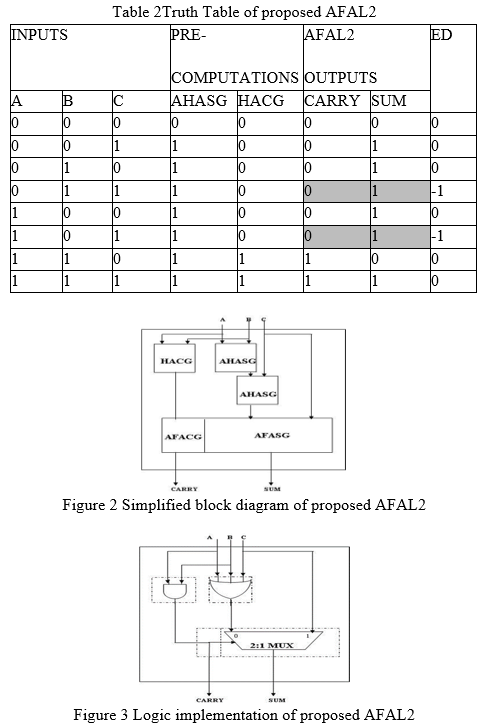
2. Approximate Full Adder Logic 2 (AFAL2)

Multiplexer-based AFAL2 is proposed to achieve great speed, energy, and area efficiency. Figure 2 depicts a simplified block design of the proposed AFAL2. To obtain sum and carry Equations, follow the procedures below.

a. Approximate Half Adder Sum Generation of two cascaded Approximate Half Adder (AHASG).

b. Generation of traditional Half Adder Carry (HACG).

c. Approximate Full Adder Carry Generation (AFACG = HACG) generation

d. Approximate Full Adder Sum Generation (AFASG) is generated by choosing one of the AHASG outputs or the "C" input.

X = ???? + ???? +  , ???????????????????? = ???? = ????. ???? . ????????????  =   ????′. X + ????. ????

The logic implementation of AFAL2, which contains two OR gates, one AND gate, and a multiplexer, is shown in Figure 3. Multiplexer's underlying logic implementation consists of four fundamental logic gates. As a result, AFAL2 has seven fundamental logic gates and two faults out of eight cases. In a simulation procedure, the suggested AFAL2's carry propagation has one logical delay. If there is an error in the carry output, the sum output selects the appropriate approximation pre-computation logic as shown in Table 2.

3. Approximate Full Adder Logic 3 (AFAL3)

The goal of AFAL3 is to reduce gate switching activity in carry propagation in order to save energy and space. Furthermore, for a critical route delay of big word size adders, the carry propagation delay of a single bit adder is minimised. The following are the logic functions of the proposedAFAL3:

a. Approximate Full Adder Carry Signal Generation (AFACG) with the shortest critical route time and the least amount of error.

b. Generation of an Approximate Half Adder Sum (AHASG).

c. Generation of traditional Half Adder Carry (HACG).

d. Approximate Full Adder Sum (AFASG) generation by choosing one of the AHASG or HACG outputs.

X = ???? + ????             (3.7)

???? = ????. ????                (3.8)

???????????????????? = ????          (3.9)

???????????? =   ????. X + ????. ????           (3.10)

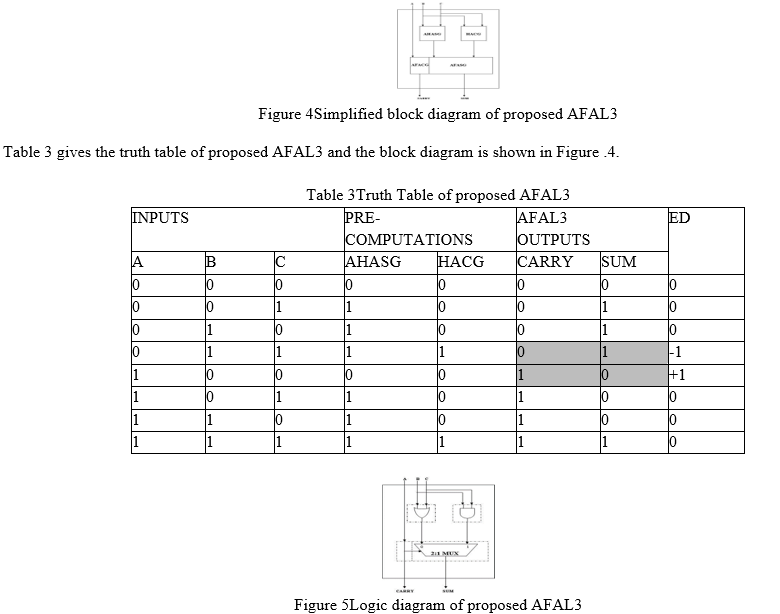
The overall logic diagram of AFAL3, which contains six fundamental logic gates, is shown in Figure 5. In addition, the most important bit of the input A is picked directly in the carry propagation to reduce the output capacitance at the carry output and to increase speed. As a result, if there is an issue in AFACG, the MSB of A selects the suitable pre compute logic instead of the exact sum as shown in Table 3. Out of eight examples, AFAL3 has two mistakes. As a result, if there is an error in the carry output for any combination of input values, there is also an error in the total output owing to the pre computation selection, which minimises the error distance by generating a compensatory deviation in the combined output value. The AHASG output is picked if the input „A = 0,” else the HACG output is selected in the AFASG output. The carry propagation of the proposed AFAL3 contains one buffer logic gate, as indicated in Table 3.3.

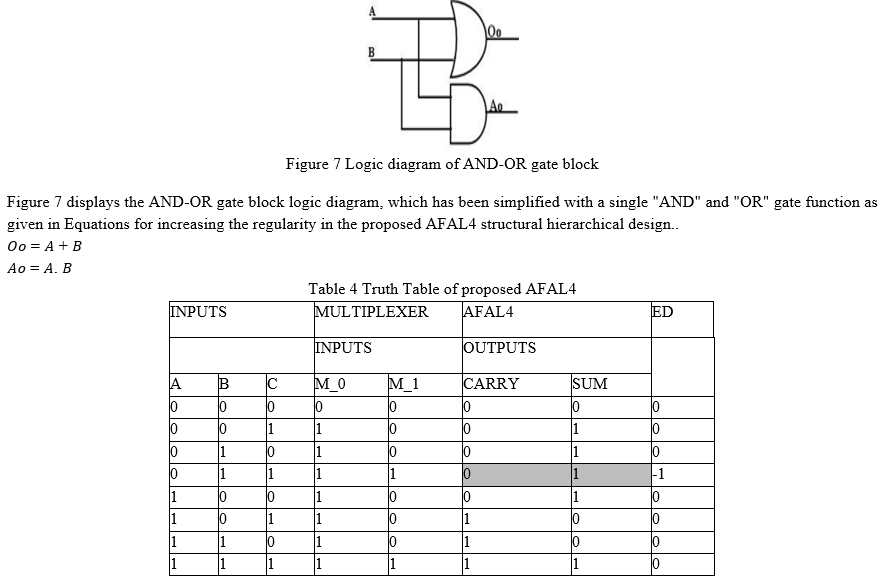
4. Approximate Full Adder Logic 4 (AFAL4)

To obtain a high pass rate, the AFAL4 algorithm is presented, which has just one mistake in eight scenarios. As shown in Figure 6  Logic Level Optimization of the proposed AFAL4 has reduced AND-OR logic and multiplexer structures by employing eight basic logic gates, six logic delays in the sum output, and two logic delays in the carry propagation output. In AFAL4, the XOR gate in the carry propagation output is replaced with simple logic gates, as shown in Equation and pre computation selection is employed to provide good performance. The suggested AFAL4 logic implementation is presented in the following steps:

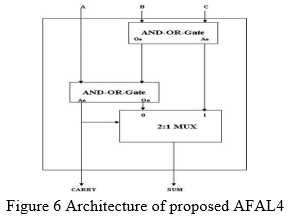
a. Equation CARRY = A is used to generate an approximation carry signal utilising a structural hierarchy of two AND-OR gate blocks. (B and C)

b. One of the multiplexer inputs M 0=A+B+C is used to generate the total of all inputs.

c. The product of two inputs is generated and applied to another input of the multiplexer M 1 = B.C.

d. If CARRY = „0,” the Total output selects the sum of all inputs; otherwise, the SUM output selects the product of two inputs, which has one mistake out of eight situations, as shown in Table.4.

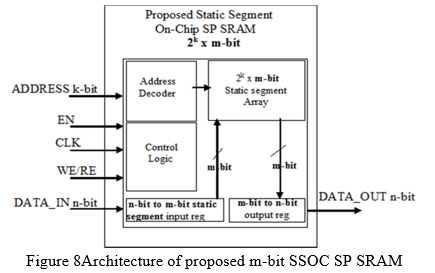
B. Proposed High-Performance Static Segmenton- Chip Memory

The design of the proposed SSOC SP SRAM is exploited in Figure 8. For error-tolerant applications, the memory's input, output register, and array size might be designed to store approximate data rather than correct data. The memory contents and output ports stay unaltered while the port input (EN) is disabled, but when the port input (EN) is enabled, memory operations may occur on the active edge of the clock input. The m-bit data is picked from the input register and saved in the appropriate memory address during an awrite operation. The memory contents at the specified address location will appear in the output register during a read operation.

The suggested m-bit SSOC SP SRAM memory area is increased over the n-bit traditional memory architecture, and the expected memory size is shown in Equation. For image processing applications, user-defined multiples data depth and data breadth memory architecture modules are offered. In place of the existing conventional SPSRAM, the suggested area efficient approximation SSOC memory architecture is employed to provide certain data-access regulations. The address decoder is used to write or read data from the storage element's successive places. Instead of a precise n-bit data storage array, the proposed SSOC SPSRAM uses an approximation m-bit data storage array. The current and next input data values are placed in the memory's next neighbouring position in a raster scan order approach. The most important bit location of the input data is used to pick the m-bit static segment, as illustrated in Figure 9 (a), where m-bit is smaller than n-bit. The minimum allowable accuracy, area, power, and acceptance probability will all drop as the segment size m-bit decreases. When the segment size is set to n bits, the proposed SSOC SP SRAM behaves like a standard SP SRAM..

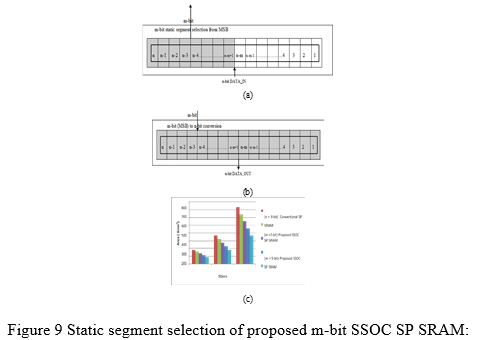
Figure 9 (b) shows how to convert m-bit to n-bit by padding "1" at an n-m bit position for better worst-case accuracy and padding "0" from n-m-1 to the output register's least significant bit position. Figure 9 shows how the anticipated area of the SSOC SP SRAM is connected to the m-bit of data for the same array size (c). The SSOC architecture presented is aimed at 45nm, 90nm, and 180nm technologies.

V. SIMULATION RESULTS AND DISCUSSION

The performance of the four suggested AFALs, CFA, and current AFAs (more than 70% pass rate, i.e. two mistakes out of eight cases) is studied and assessed in a basic logic gate framework.

A. Logical Gate Count and Delay Analysis of Full Adders

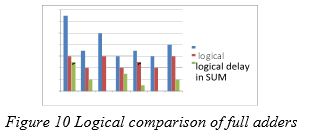
Figure 10 Logical comparison of full adders

Figure 10 depicts the number of logical gates and the time it takes to generate sum and carry in proposed and current complete adder logics. The logical gate count in AFAL1 and AFAL3 is lower than in any other logic design. Furthermore, as compared to the other AFALs, AFAL3 has a shorter carry propagation time. AFAL3 is the best in terms of logical gate count and latency.

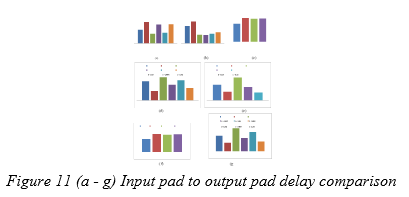
B. Area and Critical Path Delay Analysis in FPGA Implementation

The suggested designs occupy two numbers of four input Look Up Tables (LUTs) in an FPGA implementation, although critical route durations are different. The crucial route delay comparison is shown in Figure 11 (a-g)..

C. Design Metrics Analysis using Cadence Compiler

Table 5 shows that the suggested AFAL1 and AFAL3 designs use the same amount of space as the other options, which is less. While the planned AFAL2 has a shorter critical path delay and consumes less power, the AFAL3 has a longer critical path delay. As a result, when compared to the previous full adder techniques, the proposed AFAL1 and AFAL3 designs have much lower area-delay product and power-delay product, as illustrated in Figure 12. When comparing AFAL3 to other adders, Table 5 shows that it consumes less overall power. When it comes to delay computation, AFAL2 performs worse than other adders. In terms of all design criteria studied, AFAL1 and AFAL3 outperform..

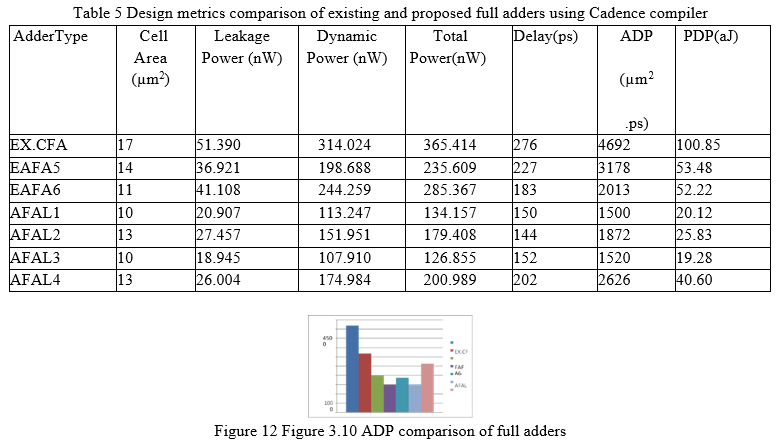
According to Figure 3.10, AFAL1 and AFAL3 have lower ADPs of 1500 and 1520 m2.ps, respectively. AFAL1 has a lower ADP than EXCFA, EAFA5, EAFA6, AFAL2, AFAL3, and AFAL4 (68.03 percent, 52.80 percent, 25.48 percent, 19.87 percent, 1.32 percent, and 42.82 percent, respectively).

D. Simulation Environment And Result Analysis of Mbit SSoc

This section compares the overall statistics of the proposed m-bit SSOC SP SRAM to the existing n-bit conventional SP SRAM using simulation and synthesis data. The design metrics of all modules are evaluated using Cadence Encounter (R) simulation, which is based on a gate level Application Specific Integrated Circuits (ASIC) TSMC 90nm technology. Xilinx14.2 and MATLAB compilers are used to perform exhaustive quality and error metrics on the proposed memory.

1. Design Metrics Analysis: The design parameters for the 16-bit data and 8-bit data conventional and m-bit suggested memory are shown in Tables 6 and 7. In 1K memories with a 16-bit data width, the estimated data storage of proposed 14-bit, 12-bit, and 10-bit SSOC SP SRAM takes up 12.17 percent, 24.50 percent, and 37.11 percent less space than 16-bit conventional SP SRAM. A similar pattern may also be seen in terms of electricity use. When it comes to total power consumption, the proposed 10-bit SSOC SP SRAM uses roughly 40% less than the present 16-bit conventional SP SRAM. Furthermore, the suggested 10-bit SSOC SP SRAM has a 12.32 percent lower latency than standard 16-bit memory.

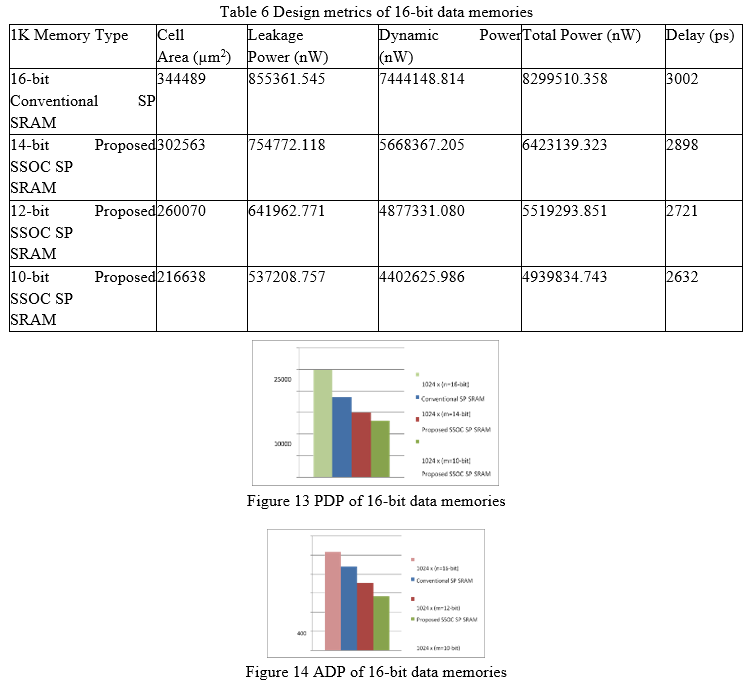
The Power Delay Product (PDP) and Area Delay Product (ADP) of 16-bit data width memory are shown in Figures 13 and 14. The PDP and ADP of the 10-bit SSOC SP SRAM are lowered by 47.81 percent and 44.87 percent, respectively, when the rate of memory data width in data storage array is dropped from 16-bit to 10-bit, as shown in Figures 13 and 14.

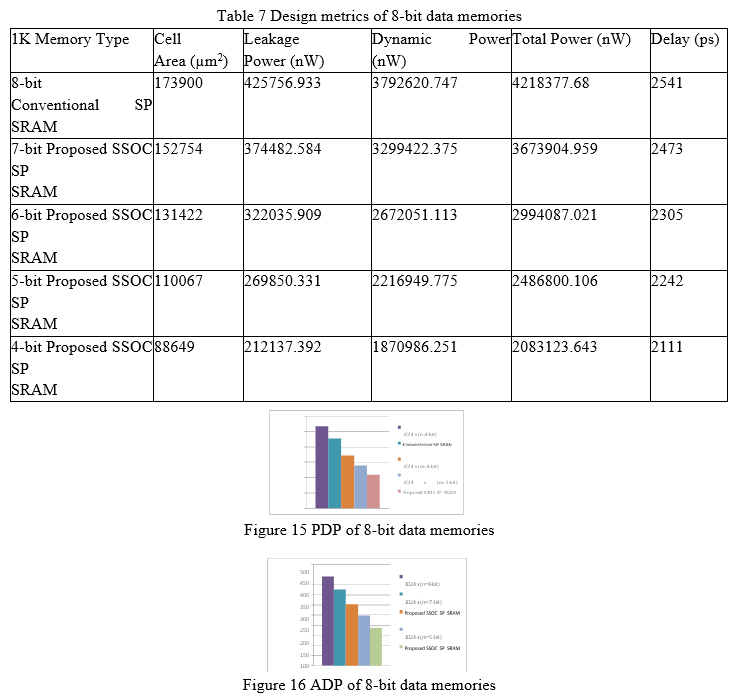
When compared to the existing 8-bit conventional SP SRAM, the proposed 4-bit SSOC SP SRAM occupies 49 percent less space, uses 50 percent less power, and has a 16.92 percent lower latency, as shown in Table. Figures 15 and 16 indicate that the proposed 4-bit SSOC SP SRAM has 58.98 percent less PDP and 57.69 percent less ADP than an 8-bit conventional memory. As a result of the foregoing design characteristics, the proposed SSOC SP SRAM core is more effective at computing large amounts of data for error-tolerant applications..

VI. FUTURE SCOPE

The performance of the proposed modules can be enhanced by,

• Incorporating the proposed adder modules into the data route unit and the proposed SSOC memory modules into the memory unit of appropriate accuracy-based error tolerant applications.

• For hybrid real-time applications, a high-performance error-tolerant reconfigurable adder may be developed at the chip level. For optimum performance, the variable accuracy range may be properly and continually checked

Conclusion

To achieve 99.8437 percent overall computational accuracy, the 16-bit High Performance Error Tolerant Adder 1 (HPETA1) is constructed employing single bit Approximation Full Adder Logic 1 (AFAL1). Furthermore, multiplexer-based hardware is proposed for AFAL2, AFAL3, and AFAL4 for simplicity of testability and reliability. The suggested AFAL2, AFAL3, and AFAL4 approximation full adders outperform other approximate full adders on the evaluated design criteria. The m-bit SSOC memory architectures are suggested in the next phase, which have lower area, access time, and power consumption in design parameters while losing some average accuracy by lowering the size of the storage array element compared to traditional on-chip memory. . The proposed 4-bit SSOC SP SRAM design provides the same quality output images with 49 percent area savings, 50 percent power reduction, and 16.92 percent speed improvement over the existing 8-bit conventional SP SRAM in image processing applications, according to a comparative study of overall balanced performance in the design and quality metrics. Based on a comparison of overall balanced performance in design and quality parameters, the suggested high-performance adders and memory VLSI architectures are better appropriate for specialised and actual image processing applications.

References

[1] Adnan, AN, Rizwan, A, Damian, D & Ronald, FD 2015, \'Designing energy- efficient approximate adders using parallel genetic algorithms\', Proceedings of Southeast Conference, pp. 1–7. [2] Andrew, B & Seokhyeong, K 2012 \'Accuracy-configurable adder for approximate arithmetic designs\', Proceedings of 49th ACM/EDAC/IEEE Design Automation Conference. doi: 10.1145/2228360.2228509. [3] Ang, SS, Constantinides, GA, Luk, W & Cheung, PYK 2008, \'Custom parallel caching schemes for hardware-accelerated image compression\', Journal of Real-Time Image Processing, vol. 3, no. 4, pp. 289-289. [4] Biedermann, A & Molter, HG, 2010, \'Secure Embedded Systems\', Springer- Verlag, Berlin Heidelberg. [5] Breuer, MA & Zhu, H 2006, \'Error-tolerance and multi-media\', Intelligent Information Hiding and Multimedia Signal Processing, 2006. IIH-MSP\'06. International Conference on, pp. 521-524. [6] Chang, TY & Hsiao, MJ 1998, \'Carry-select adder using single ripple- carry adder\', Electronics Letters, vol. 34, no. 22, pp. 2101-2101. [7] Christe, SA, Vignesh, M & Kandaswamy, A 2011, \'An Efficient FPGA Implementation of MRI Image Filtering and Tumor Characterization Using Xilinx System Generator\', International Journal of VLSI design & Communication Systems (VLSICS), vol. 2, no. 4, pp. 95-109. [8] Darjn, E, Gerardo, C, Davide, DC, Ettore, N, Nicola, P & Antonio, GM 2016, \'Approximate adder with output correction for error tolerant applications and Gaussian distributed inputs\', Proceedings of IEEE International Symposium on Circuits and Systems, pp. 1970–1973. [9] Garg, B, Dutt, S & Sharma, GK 2016, \'Bit-width-aware constant-delay run- time Accuracy Programmable Adder for error-resilient applications\', Microelectronics Journal, vol. 50, pp. 1-7.s [10] Geetha, S & Amritvalli, P 2017, \'High Speed Error Tolerant Adder for Multimedia Applications\', Journal of Electronic Testing, vol. 33, no. 5, pp. 675-688. [11] Gupta, V, Mohapatra, D, Raghunathan, A & Roy, K 2013, \'Low-power digital signal processing using approximate adders\', IEEE Transactions on Computer- Aided Design of Integrated Circuits and Systems, vol. 32, no. 1, pp. 124-137. [12] Haider, AF, Almurib, T, Nandhakumar & Fabrizio, L 2016, \'Inexact Designs for Approximate Low Power Addition by Cell Replacement\', Proceedings of Design, Automation & Test in Europe Conference & Exhibition, pp. 660–665. [13] Hu, J & Qian, W 2015, \'A New Approximate Adder with Low Relative Error and Correct Sign Calculation\', DATE Workshop, pp. 1449-1454. [14] Irina, A & Lau, KT 2017, \'Approximate adder for low-power computations\', International Journal of Electronics Letters, vol. 5, no. 2, pp. 158–165. 28. [15] Ing, CL, Yi, MY & Cheng CL 2015, \'High-performance low-power carry speculative addition with variable latency\', IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 23, no. 9, pp. 1591– 1603. [16] Junjun, H & Weikang, Q 2015, \'A New Approximate Adder with Low Relative Error and Correct Sign Calculation\', Proceedings of Design, Automation & Test in Europe Conference & Exhibition, pp. 1449–1454. [17] Juurlink, B & De Langen, P 2004, \'Dynamic techniques to reduce memory traffic in embedded systems\', Computing Frontiers Conference, pp. 192-201. [18] Kahng, AB & Kang, S 2012, \'Accuracy-configurable adder for approximate arithmetic designs\', Proceedings of the 49th Annual Design Automation Conference on - DAC \'12, pp. 820-820

Copyright

Copyright © 2022 Burhan Khalid Khan, Mr. Ritesh Ojha. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.