Development of Cyclic Stress-Strain Curves for Modified Rat-Trap Bond Concrete Brick Masonry from Experimental Investigations

Abstract

Present study is based upon the experimental results obtained by reloading and unloading of concrete brick masonry samples constructed in modified rat-trap bond under uniaxial compression perpendicular to their bed joints. Considering the advantage of air gap between perpends for thermal comfort, Flemish bond was modified as rat-trap bond using half scale modular bricks (95mm × 95mm × 45mm) and called Modified Rat-Trap bond concrete brick masonry. The air gap created within the wall was filled up with insulating material thermocol (Expanded polystyrene). General polynomial expression has been developed for both reloading and unloading curves separately which were found suitable to predict the behavior of said masonry at any given residual strain. With the help of this parent polynomial, the particular reloading and unloading curves are then developed by transferring the parent equation to stress-strain coordinate. It was observed that the nature of reloading and unloading curves is primarily influenced by plastic strain. A fair consistency was observed between the experimental and computed curves.

Introduction

I. INTRODUCTION

Analytical model in order to predict the behavior of reloading and unloading curves under uniaxial compressive cyclic loading for brick masonry have been developed by Naraine and Sinha (1989), Subramanium and Sinha (1995), Alshebani (1999), Alshebani and Sinha (1999), Senthivel (2002), Singh B.K et al. (2004), Maqsud E.Nazar et al.(2007), Lorenzo et al. (2014), Luca Facconi et al. (2018).

In the present study an effort has been made to develop analytical model for reloading unloading curves for modified rat-trap bond brick masonry.

It reveals from literature survey that Rat-Trap bond brick masonry is a better substitute to low cost housing up to two stories buildings which is the need of millions of people residing either in rural or urban areas of the country.

In India, which has different climatic zones associated with drastic weather change within a climatic zone, the rat-trap bond brick masonry is the most suitable option.

The technique adopted in Rat-Trap bond has been implemented in many government affordable housing schemes but in a limited no. basis due to lack of structural testing of such walls.

The extensive use of Rat-Trap bonded wall is possible only when if proper experimental investigations are done.

Considering the advantage of air gap between perpends for thermal comfort, Flemish bond was modified as rat-trap bond using half scale modular bricks (95mm × 95mm × 45mm) and called Modified Rat-Trap bond brick masonry. The air gap created within the wall was filled up with insulating material thermocol (Expanded polystyrene) and its structural behavior was evaluated by loading it perpendicular to the bed joint. The fly ash cement bricks used in the construction help to reduce the pollution level by consuming fly-ash, a by-product of thermal power plants which are responsible for air pollution. The use of fly ash bricks also reduce the consumption of virgin material like soil, mud which are used at large scale in manufacturing clay bricks.

An attempt has also been made to develop a suitable mould that can allow locally available materials for manufacturing of masonry units close to construction site, thereby increasing the economic viability and sustainability of the product.

The present study discusses the unloading and reloading behavior of modified rat-trap bond masonry under uniaxial cyclic compressive loading perpendicular to the bed joint. The analytical model represents the influence of the residual strain on the behavior of loading as well unloading curves and therefore the model equation is expressed in terms of non- dimensional axial strain and non- dimensional plastic strain.

II. EXPERMENTAL PROGRAM

A. Selection of Material

1. Cement: The cement used was 43grade Ordinary Portland Cement.
2. Fly Ash: The fly ash used in the production of fly ash bricks was chimney fly ash procured from Thermal Power Plant, Dadri, U.P., India.
3. Aggregate: The fine aggregate used in the production of fly ash bricks as well as in mortar was locally available land quarried Badarpur sand which confirms to grading Zone II of IS: 383-1970.
4. Water: The quality of water used in the production of fly ash bricks, in mortar as well as for curing of bricks and walls was potable water available in the laboratory conforming IS:456-2000.
5. Mix Proportion: Mix proportion for preparing cement fly ash bricks was decided by trial and error method to get the target strength of modular bricks as 15N/mm2.

Cement: Fly ash: Sand: Water = 1: 1: 4: 0.60

Similarly, for mortar, the mix proportion decided was

Cement: Sand=1:5

B. Dimensions of Modular Bricks and Wallets

 Modular Bricks: 95 mm × 95 mm × 45mm (Half scale)

 Wallets:             495 mm × 545 mm × 95 mm

C. Loading Arrangement

The entire test specimens were tested on a Universal Testing Machine of 1000KN capacity attached with control panel and interfaced with computer panel. Axial load was applied through hydraulic pressure control unit. Teflon sheets of 10mm thickness were placed on bearing surface of the specimen to minimize platen effect as well to reduce friction between loading platform and the bearing surface of the specimen. The loading arrangement has been shown in the following figure 4.

D. Instrumentation

The instrumentation for the test specimens were done for the measurement of axial and lateral displacement with the fix gauge lengths. A mutually perpendicular biaxial types (+) strain gauge (gauge length 60mm, gauge resistance 120 ohm and gauge factor 2.13) were glued in position using araldite, an epoxy resin on both the faces of brick panel. The strain gauge connected in parallel to data acquisition system which was further connected with P.C. This was used to display, monitor and record the deformation with load in real time.

E. Test Procedure

Three types of test were conducted on modified rat-trap bond brick masonry panels as well as on conventional brick masonry panels. Three specimens were tested for each type of test I.e. monotonic loading test, common point test and stability point test.

1. Type I test (Monotonic loading test):  In this type of test, the load was applied uniaxial and increased steadily to failure. The rate of loading applied was such that the failure of the specimen was reached in about 3 to 5 minutes.
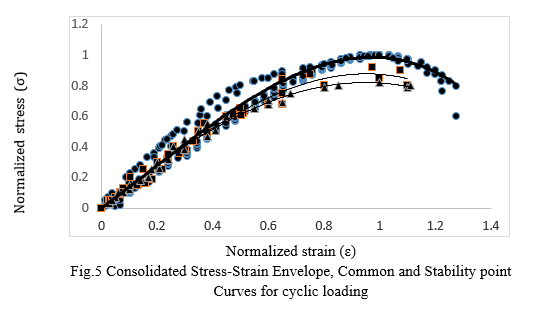
2. Type II test (Common point test):  In this type of test uniaxial cyclic load was applied on the specimen. In the cyclic loading, the specimens were loaded up to peak stress-strain curve as obtained from monotonic load test and then unloading started. In this way, the peak stress-strain in each cycle of loading followed almost the same curve as obtained from envelope curve from monotonic test. The envelope curve is the locus of limiting values of stress-strain within which all stress-strain curves lies irrespective of the loading pattern. Load histories were controlled by monitoring either stress level or incremental strain during a given cycle. The loading was done at a stress rate of approximately 3 N/mm2 per minute and unloading was done at the rate of 6 N/mm2 per minute by hydraulic pressure unit. The rate of increment of strain from 0.4x10-3 to 0.5x10-3 in each cycle was found appropriate for loading curve to reach the envelop curve. The unloading was done in the descending zone when the loading curve tended to descend. The point of intersection of reloading curve with unloading curve of previous cycle is called common point and the locus of points where reloading curve crosses the unloading curve of previous cycle on stress-strain curve is called common point curve.
3. Test type III (Stability point test): In this type of test cyclic load was applied in the similar manner as per common point test, the only difference is that in stability point test, reloading and unloading was repeated a number of times in each cycle of loading. Every time unloading was done when the reloading curve intersected the unloading curve of previous cycle until such intersection point which is descending in nature, got stabilized. At this stage, locus of common point stabilized at lower bound and the further cycles of loading lead to formation of hysteresis loop. The lower bound point at which the common point stabilized is called stability point.

III. TEST RESULTS AND VEVALUATIONS

A. Stress-Strain Coordinate System

The coordinate system adopted in the present study is non-dimensional coordinates. The stress coordinate (?) is normalized with respect to peak stress (?m) and the strain (e) coordinate is normalized with respect to (em), which is the strain corresponding to peak stress (?m ).

IV. UNLOADING AND RELOADING STRESS-STRAIN CURVES

The Analytical models for reloading and unloading curves of modified rat-trap bond brick masonry tested uniaxial cyclic compressive loading are proposed as follows.

A. Reloading Stress-Strain Curves

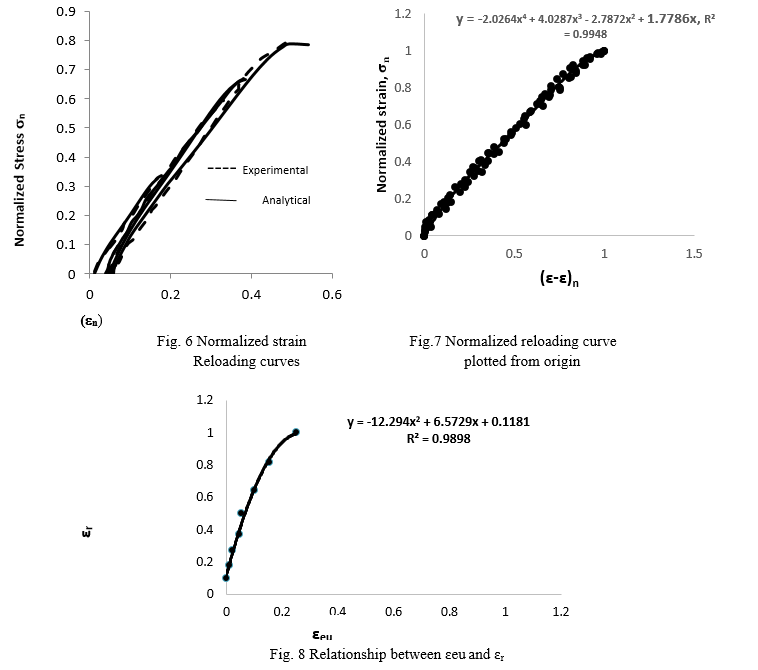
The representative experimental reloading stress-strain curves of modified rat-trap bond masonry under uniaxial repeated compressive loading are shown in fig.6. The curves are drawn on the normalized stress-strain coordinate system (e-sn). Each reloading curves starts at a certain value of normalized plastic strain (er) and terminates when it touches the envelope stress-strain curve. Normalized plastic strain is the ratio of the plastic strain to the strain (eeu) corresponding to the peak stress. Plastic strain is significant parameter in the determination of reloading curves. The mathematical modelling for the reloading curves has been developed by transferring all the reloading curves at a common origin. The reloading curves plotted on e verses s coordinate system transferred to the (e-er) verses s coordinate system. Now the all the curves are again transferred to a new coordinate system in which (e-er) coordinate was normalized with respect to (eeu-er) whereas s coordinate normalized with respect to seu for each reloading curve. In this way, in the new coordinate system, each curve originates from (0, 0) and terminates on (1, 1). On transferring all the reloading curves to the new coordinate system (e-er)n verses sn, the plots are confined to a narrow band which can be seen in fig.7. The method of least square is used to compute a parent polynomial curve to fit in the test data. Following is the general equation of the polynomial curve.

sn =a (e-er) 4 +b (e-er) 3+c (e-er) 2+d (e-er)                     (i)

Where,

sn                 =s/seu

(e-er)n           =(e-er)/ (eeu- er)                                                                     (ii)

s                     =non-dimensional axial stress

sn                    = non-dimensional stress at any point on the envelope

                       Curve

seu                  = non-dimensional stress at the start of unloading on

                       the envelope curve

e                      = non-dimensional axial strain

eeu                   = non-dimensional strain at the start of unloading on the 

                     Envelope curve corresponding to seu

er   = non-dimensional plastic strain at the end of unloading

a, b, c and d = equation parameters

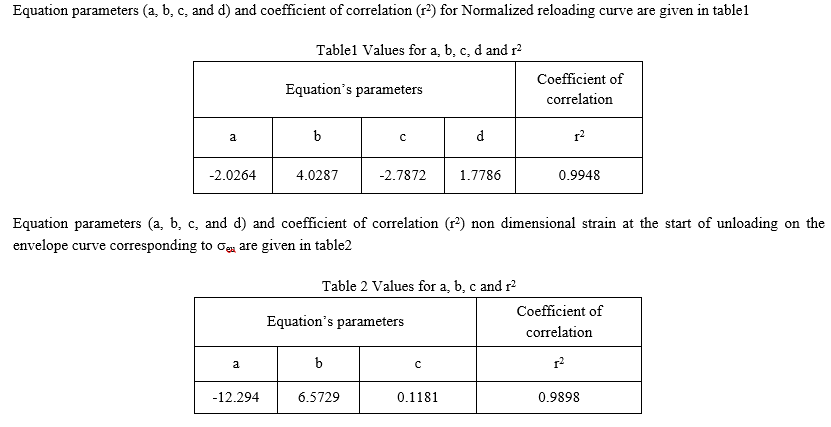
The above parent polynomial expression (i) is used to generate individual stress-strain curve. In order to transfer the parent equation from (eeu-er)n coordinate system to (e-s) coordinate system the values of eeu and seu are required to be known. The can be done by plotting

eeu verses er as shown in fig.8.

It may be observed from the plotting that the relation between eeu and

er is parabolic and second degree polynomial curve was found to fit into the experimental data. The general expression for the above may be represented in the following form.

                       eeu =a er2 +b er + c                (iii)

         Where, er   = non dimensional plastic strain at the end of unloading

                       eeu = non dimensional strain at the start of unloading on the

                               Envelope curve corresponding to seu

                    a,b,c    = equation’s parameters

B. Unloading Stress-Strain Curve

The experimental normalized stress-strain unloading curves for modified rat-trap bond under compressive uniaxial cyclic loading are shown in fig.9. Each unloading curve starts from the envelope curve (eeu, seu ) and terminates at particular value of er. It is observed from these unloading curves that the degree of curvature increased with decrease of stress level. In case of unloading begins after ultimate stress i.e. at larger envelope strain, the softening shown by unloading curves at lower stress level is more. 

The process for the development of analytical model for unloading curve is similar to the development of analytical model for reloading curve. All the unloading non dimensional curves (e,s) have been plotted on a common origin by adopting (e-er) versess coordinate system. Again these curves are transferred to a new coordinate system in which (e-er) coordinate is normalized with respect to (eeu- er) and s coordinate normalized with respect to seu. The new coordinate system has now become (e-er)n verses sn in which each curve originates from (0,0) and terminates at (1,1). This results a plot of unloading curves in a narrow band of points as shown in fig.10.

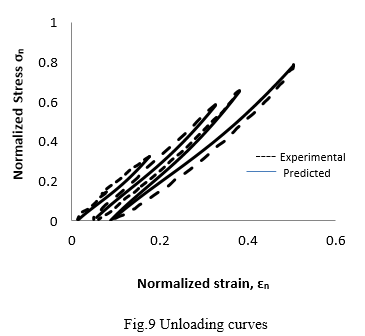
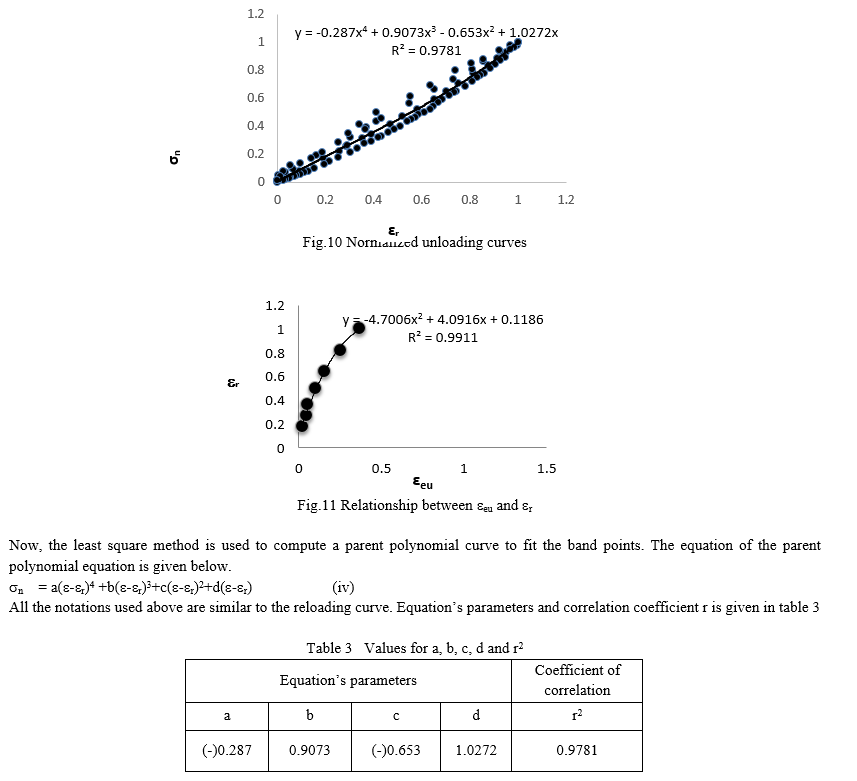
The parent polynomial expression is used to generate individual unloading curve. In order to transfer the coordinate system (e-er)n verses sn into e verses s coordinate system the values of er and seu for a particular value of eeu is required to be known. For each cycle of loading curve starting at a particular value of eeu, the value of er is different. The plot of eeu verses er is shown in fig.11. On best fitting of observed data, a second degree polynomial is obtained which is as follows:

Where all the notations are similar to the case of unloading curve. The equation’s parameters and coefficient of correlation are given in Table 4 below.

Table 4 Values for a, b, c and r2

The following are the steps for computing unloading curve.

1. For a given value of non-dimensional plastic strain (er), the value of non- dimensional strain (eeu) at the start of unloading curve corresponding to non-dimensional stress (seu) on the envelope curve is calculated by equation (iii)
2. For the above calculated values of eeu , the corresponding values of (e-er)n are calculated using equation (ii)
3. The different values of sn are calculated using different values of e from the origination to termination point with the help of equation (i)

The values of s corresponding to a particular value of e are computed by multiplying sn by se

Conclusion

The present study aims to develop analytical model for reloading unloading curves for modified rat-trap bonded masonry Considering advantage of air gap between perpends for thermal comfort, Flemish bond was modified as rat-trap bond and called Modified Rat-Trap bond brick masonry. The air gap created within the wall was filled up with insulating material Thermocol (EPS) and its structural behavior was evaluated perpendicular to the bed joint. The fly ash cement bricks used in the construction help to reduce the pollution level by consuming fly-ash, a by-product of thermal power plants which are responsible for air pollution. Cement, fly-ash, fine aggregate, water was used in the ratio 1:1:4:0.6 to produce cement fly ash bricks to half the scale of modular bricks. The size of bricks used in the construction of wallets was 95mm × 45mm × 45mm. The proportion of mix was decided on the basis of several trials considering the strength, optimum moisture content, demolding. Test were conducted on wallets of size 540mm × 495mm × 95mm for three types of tests: (i) Monotonic test (ii) Common point test (iii) Stability point test under uniaxial repeated compressive loading Based upon experimental data and method of least square single mathematical polynomial expression is proposed for normalized envelope, common point and stability point curves. The tangent and secant modulus of elasticity at forty percent of ultimate load are nearly equal. An analytical model for predicting reloading unloading curves at any given residual strain has been proposed in form of a general polynomial equation. The model involves transferring of reloading unloading curves to a new normalized coordinate system with common origin. Now the all the curves are again transferred to a new normalized coordinate system in which the plots are confined to a narrow band. The method of least square is used to compute a parent polynomial curve to fit in the test data on this coordinate system. The particular reloading and unloading curves are then developed by transferring the parent equation to the stress –strain coordinate system. It was observed that the natures of reloading unloading curves are primarily influenced by plastic strain. A good correspondence was observed between experimental curves and analytical curves.

References

[1] Alshebani, M.M. (1999). “Response of Brick Masonry under Cyclic Loading.” Ph.D. Thesis, Indian Institute of Technology, Delhi, India. [2] Alshebani, M.M. and Sinha S.N. (1999), “Stress-Strain characteristics of Brick Masonry under Cyclic Loading. “Journal of Structural Engineering, ASCE, Vol.125, No.6, 600-604. [3] Aslani F. (2010), “A Comparative Study of Cyclic Consecutive Model for Concrete.” M.Sc. Thesis, University of Kurdistan, Sanandaj, Iran. [4] C. Jayasinghe, H.D.D. Lakmali and M.P. Rohitha. “Comparative Performance of Masonry Bond Patterns, Annual Transaction of IESL 2018 pp. 38-46. [5] MaqsudE.Nazar, S.N.Sinha (2007), “Loading-Unloading Curves of Interlocking Grouted Stabilized Sand-Fly Ash Brick Masonry.” Material of Structures, Vol. 40, Issue 7, pp. 667-678. [6] P.Ghatee M.S. Jaffar, A. Ibrahim and HamedTalati, (2017), “Modelling the Damage Characteristics of Concrete subjected to Cyclic Loadings.” Mechanics of Composite Materials. [7] SerhanGuner, “Numerical Modeling of a Cassion Foundation Retrofitted with Helical Piles.” Conference paper, July (2018).

Copyright

Copyright © 2022 Dr. Sunil Prasad Shrivastava. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.