Energy Efficient Approximate 8-bit Vedic Multiplier

Abstract

The digital signal processing and its classification applications on the energy constrained devices should be supported based on efficiency. Because such applications must perform highly complex computations especially complex multiplication processes while exhibiting tolerance for a large amount of noise and for computational errors too. So, comparing all the arithmetic computations, improving the energy efficiency of multiplication is critical. In this project, an energy efficient approximate 8-bit Vedic multiplier is proposed which gives a tradeoff between computational accuracy and energy consumption. The proposed architecture has reduced area compared to other multiplier architectures which process same number of bits. The reduced architecture area reduces the power consumption. Also, the Vedic technology adopted for the multiplication reduces the delay further. But the approximate architecture output possesses a small amount of computational accuracy which is negligible for DSP applications.

Introduction

I. INTRODUCTION

For today’s electronic world embedded system and mobiles, energy consumption is a critical design problem lot of efforts have already been taken at various levels for improving the energy efficiency. Among other arithmetic operations, multiplication is the most time and power consuming operation. It becomes more significant for large operands and complex multiplication. Considering these constraints, a new approximate multiplier is proposed. This new method can provide much more energy efficiency than the truncated methods. The error rate is low because it effectively captures the noteworthy lower bits. For DSP and its classification algorithm, generally one of two operands in the multiplication is stored in the memory. Here it is exploited to improve the energy efficiency of the approximate multiplier further. The area can be effectively reduced by the proposed approximate multiplier because many adders and gates can be excluded in this method as compared to other multipliers. Within the approximate multiplier architecture, a Vedic technology is used for the multiplication which reduces the delay in the multiplication. As the scale of integration keeps growing, more and more sophisticated signal processing systems are being implemented on a VLSI chip. These signal processing applications not only demand great computation capacity but also consume considerable amount of energy. While performance and Area remain to be the two major design tolls, power consumption has become a critical concern in today’s VLSI system design. The need for low-power VLSI system arises from two main forces. First, with the steady growth of operating frequency and processing capacity per chip, large currents must be delivered and the heat due to large power consumption must be removed by proper cooling techniques. Second, battery life in portable electronic devices is limited. Low power design directly leads to prolonged operation time in these portable devices. Multiplication is a fundamental operation in most signal processing algorithms. Multipliers have large area, long latency and consume considerable power. Therefore, low-power multiplier design has been an important part in low power VLSI system design. There has been extensive work on low-power multipliers at technology, physical, circuit and logic levels. A system’s performance is generally determined by the performance of the multiplier because the multiplier is generally the slowest element in the system. Furthermore, it is generally the most area consuming. Hence, optimizing the speed and area of the multiplier is a major design issue. However, area and speed are usually conflicting constraints so that improving speed results mostly in larger areas.

II. MULTIPLIER MODULE

A. Vedic Multiplier

The Booth multiplication algorithm and Array multiplication algorithm are associated with high propagation time. But the fast multiplication process is defined by Vedic Mathematics. The Veda means store of knowledge. The Vedic mathematics means storage of knowledge of mathematics related to the high-speed operations.

This Vedic mathematics provides the knowledge of varies area of mathematics like arithmetic, algebra, geometry using 16 important sutras. The method given in the Vedic math's is very simple. The Jagadguru Shankaracharya Bharati Krishna Teerthaji Maharaja has combined all concepts together and given its explanation. Out of 16 sutras the Urdhva-Tiryagbhyam Vedic Sutra is very much useful multiplication operation. Present work is an effort to design and implement the multiplier using Urdhva- Tiryagbhyam Vedic Sutra.

B. Urdhva-Triyagbhyam Sutra and its Implementation

The Urdhva Tiryagbhyam sutra is based on vertical and crosswise multiplication algorithm. This sutra enables the parallel generation of intermediate products and eliminates unwanted multiplication steps. This type of multiplier takes a form of one of the low powers and high-speed multiplier.

Design: Urdhva Triyagbhyam means “Vertically and Crosswise”, which is the method of multiplication followed. For the Vedic multiplication consider a 4×4 multiplier whose operands are A3A2A1A0 and B3B2B1B0.For the multiplication of a single bit a simple AND gate is used. So, the generalized equations for the output bits of 4X4 Vedic multiplier can be written as:

1. S0=A0B0
2. S1=A0B1+A1B0
3. S2=A0B2+A1B1+A2B0+previous carry
4. S3=A0B3+A1B2+A2B1+A3B0+previous carry
5. S4=A1B3+A2B2+A3B1+previous carry
6. S5=A2B3+A3B2+previous carry
7. S6=A3B3

The S7 bit is the carry of the previous addition process. Thus, 8bit output is been obtained.

The block diagram of this sutra in being referred in the Fig. 1-

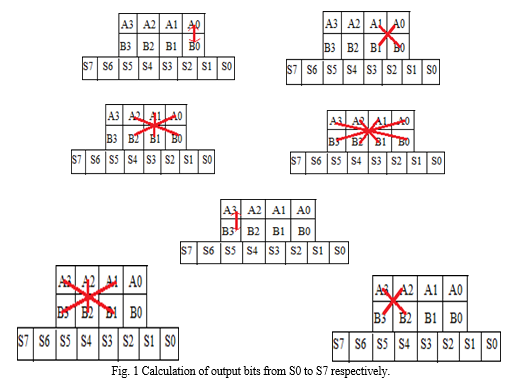
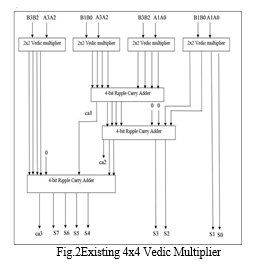
  Using four 2x2 bit Vedic multipliers and 3 adders we can build 4x4 bit Vedic multiplier as shown in Fig. 2 with proper instantiating of the 2x2 Vedic multipliers and adders. First 2x2 bit Vedic multiplier has inputs as A1A0 and B1B0. The last block is also 2x2 bit Vedic multiplier with inputs A3A2 and B3B2. The blocks in the middle are 2x2 bit multipliers with inputs A3A2 & B1B0 and A1A0 & B3B2. So, the result of multiplication will be of 8-bit as S7 S6 S5 S4 S3 S2 S1 S0. As compared to Array Multiplier, Vedic Multiplier is efficient in terms of delay and speed. The Vedic Multiplier can be used to reduce delay.

III. ARCHITECTURE OF APPROXIMATE 8-BIT MULTIPLIER

A. Design Process

The following steps are followed in the design of the multiplier

1. Design a basic 4-bit Adder which performs the function of 4-bit addition.
2. Design an efficient 4x4 bit Vedic multiplier using half adder, full adder and 4- bit adder.
3. Design 8x8 Vedic multiplier using 4x4 bit Vedic Multiplier and 8 Bit Ripple Carry Adder.
4. Design 8-bit selection architecture using 2:1 Mux and design a 3:1 Mux to perform shifting operations on output bits.
5. Energy consumption and delay of the circuit is estimated.

B. Proposed 4 Bit Adder

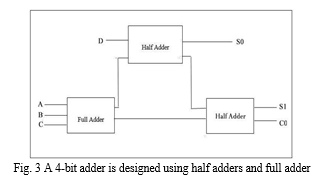
Proposed 4-bit adder performs the function of 4-bit addition that gives two bits of sum and one carry as output. Its block diagram contains one full adder (FA) and two half adders (HA) as shown in the Fig.3. Here, A, B, C, D are four inputs. S0 and S1 are LSB and MSB of Sum outputs respectively and Sum is the sum of four inputs whereas C0 is the carry bit. The delay of the 4x4 Vedic Multiplier can be further decreased by using this proposed 4 Bit Adder.

C. 4X4 Vedic Multiplier

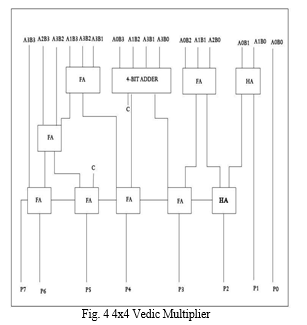
To reduce the delay, a 4x4 Vedic multiplier is implemented using half adder, full adder and the proposed 4-bit adder as shown in the Fig. 4. Here, few full adders are replaced with the half adders so that the critical path delay is reduced to a greater extent. So, the designed multiplier is much more efficient than existing Vedic multiplier. The higher bit Vedic multiplier architectures like 8-bit, 16-bit, 32-bit etc. can be built using these 4-bit Vedic multipliers. The Fig.3.2 depicts two inputs consisting of 4-bit size that results by producing an output P resulting of 8-bit size.

D. 8X8 Vedic Multiplier using 4X4 Vedic Multiplier

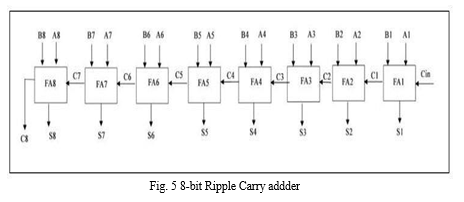
1. 8-bit ripple carry adder

A ripple carry adder is a logic circuit in which the carry-out of each full adder is the carry in of the succeeding next most significant full adder. It is called a ripple carry adder because each carry bit gets rippled into next stage as shown in Fig. 5.

The A and B are 8 bits each. A=A0 A1 A2 A3 A4 A5 A6 A7

B=B0 B1 B2 B3 B4 B5 B6 B7

A and B are added and the corresponding sum and carry is obtained. Here, S1, S2, S3, S4, S5, S6, S7, S8 is the sum.

C8 is the carry out.

2. 8X8 Vedic Multiplier

As shown in Fig. 6, the 8X8 Vedic Multiplier consists of 8-bit ripple carry adders and 4x4 Vedic Multipliers. So, 8bit inputs- a [0-7], b [0-7] are given and a 16-bit product s [15:0] is obtained.

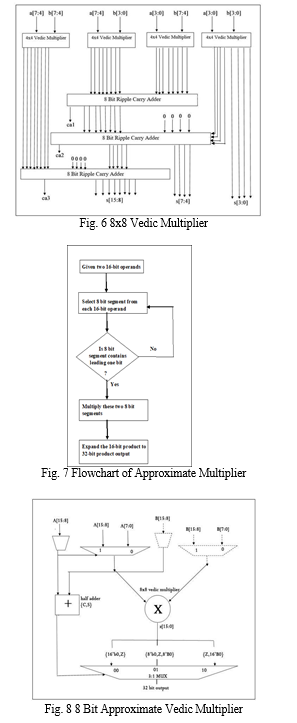
The structure of the proposed 8 Bit Selection Architecture of approximate multiplier is shown in Fig. 8. The architecture consists of two “8” bit selection units for each 16-bit operands, a multiplier unit, a 3 to 1 mux as output unit and a half adder which gives the selection bit for the output mux. Here the approximate multiplier takes only “8” consecutive bits for multiplication from each “16” bit operands. The 8-bit segment is selected only from one of two or three fixed bit positions of a positive number depending on where is its leading one bit. This technique gives a higher accuracy than simply truncating the LSBs. In this approach the 8-bit segments are selected from each operand from the leading one positions and it is then steered into an 8 × 8 multiplier (which is here a Vedic multiplier) and then the 2*8 output obtained from the multiplier is expanded to 2*16 output bits.

IV. DESIGN AND SIMULATION OF APPROXIMATE 8-BIT VEDIC MULTIPLIER

A. Simulation

The work deals with designing Approximate multiplier with 8-bit selection architecture and which also implements Vedic multiplication. So, the outputs are considered and simulated such that required operations of multiplier are verified. To obtain the delay report of project a simulating tool name XILINX ISE SUITE 14.7 is used, whereas to obtain the power report CADENCE simulating tool is used. Once all the required building blocks are designed and verified; these blocks are integrated to design the Approximate  multiplier.

B. Simulation Waveforms

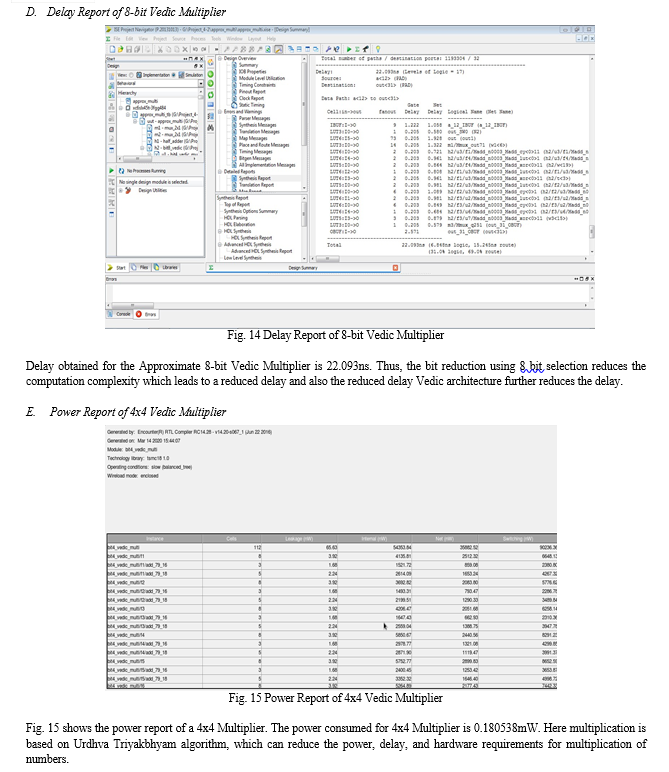
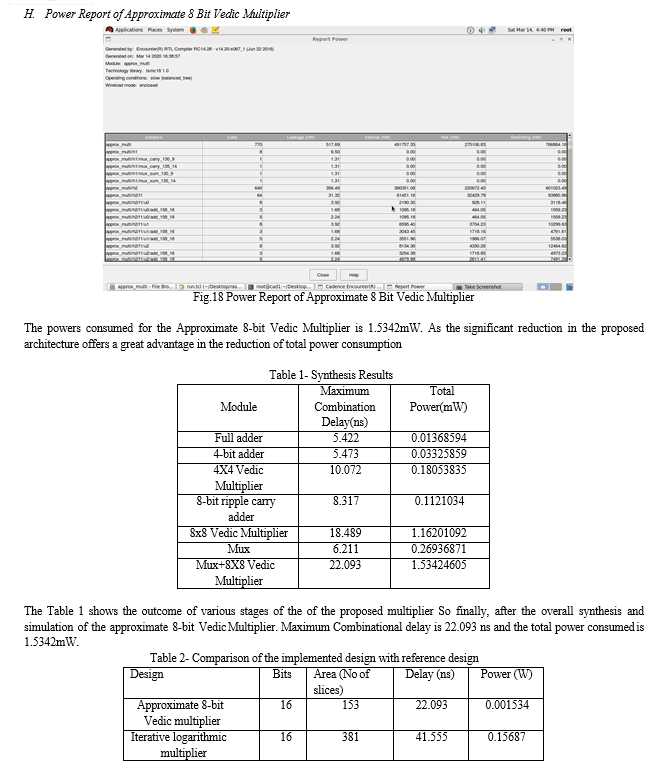
Here we compare our design for the number of slices, delay, and power consumption. The data for comparison is taken from the reference paper. Thus, the proposed approximate 8-bit Vedic multiplier is more energy efficient than the other conventional multipliers. Hence the potential applications of this approximate multiplier fall mainly in areas where there is no strict requirement on accuracy or where super-low power consumption and high-speed performance are more important than the accuracy.

VI. FUTURE SCOPE

Future scope of the work includes improving the performance of the approximate Vedic       multiplier by using Enhanced Static Segment Method for segment-based multiplication, to provide good accuracy at notably low energy consumption considerable reduction in area overhead and use of carry look-ahead adder in design of Vedic multiplier which in turn reduces the propagation delay by introducing more complex hardware.

Conclusion

Area, power consumption and increased delay are the constituent factors in VLSI design that degrades the performance of any circuit. This proposed architecture of an energy efficient multiplier in which the area, delay and power consumption are reduced to a great extent on comparing with the present works. A technique for the multiplication of 8-bit operands with the help of Vedic multiplier is described. The proposed architecture is based on “Urdhva Triyakbhyam” sutra of Vedic mathematics which is a general multiplication technique for multiplication. This algorithm makes the parallel generation of partial products and removes unwanted multiplication steps and hence results in faster multiplication. Also, with this algorithm the increase in delay and power consumption is less with the increase in number of bits. This proposed technique works in two steps. In the first step the equation for each bit of the resultant is computed. In the second step that equation is executed with the required multipliers and Ripple Carry Adders. The reduction of number of bits which takes part in multiplication reduces the complexity of the multiplication process and thus improves the efficiency. The number of, half adders and full adders used in the proposed multiplier architecture is much less than the conventional multiplier architectures. The significant reduction in the proposed architecture offers a great advantage in the reduction of area and therefore the total power consumption. Thus, the proposed 8-bit multiplier is more energy efficient than the other conventional multipliers. Also, the bit reduction using 8 bit selection reduces the computational complexity which leads to a reduced delay and also the reduced delay Vedic architecture further reduces the delay. The potential applications of this approximate Multiplier fall mainly in areas where there is no strict requirement on accuracy or where super-low power consumption and high-speed performance are more important than the accuracy. The 8-bit approximate Vedic multiplier can be used for various digital signal processing applications where complex computations are to be performed.

References

[1] K. Y. Kyaw, W. L. Goh and K. S. Yeo, “Low power high-speed multiplier for error tolerant application “, in IEEE Intl. Conf. Electron Devices and Solid-State Circuits (EDSSC), 2010, pp. 1-4. [2] Kaustubh Manikrao Gaikwad and Mahesh Shrikant Chavan,” Analysis of Array Multiplier and Vedic Multiplier using Xilinx\", in Communications on Applied Electronics (CAE), Volume 5 – No.1, May 2016. [3] Mageshwari , G.A. Sathish Kumar,” Design and Development of Approximate Multiplier Using Urdhva Algorithm”, in International Journal of Innovative Research in Computer and Communication Engineering, Vol. 5, Special Issue 3, April 2017. [4] B.Anish, Fathima, C.Vasanthanayaki,” Design and Implementation of Energy Efficient Approximate Multiplier”, International Journal of Computer Applications (0975 – 8887), NCICT (2015). [5] Sumant Mukherjee, Dushyant Kumar Soni, “Energy Efficient Multiplier for High-Speed DSP Application”, in IJCSMC, Vol. 4, Issue. 6, June 2015. [6] Pushpalata Verma, “Design of 4x4 bit Vedic Multiplier using EDA Tool”, in International Journal of Computer Applications (0975-888), Volume 48- No.20, June 2012 [7] “Synthesis and Simulation Design Guide” available at www.xlinx.com [8] “Digital Design Flow” for Cadence [9] Z. Babi´c, A. Avramovi´c, and P. Bulic, “An Iterative Logarithmic Multiplier” in 2011

Copyright

Copyright © 2022 Vijay Bhaskar Nittala, Anisha Bomma, M. Ramana Reddy. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.