Finite Element Based Static and Dynamic Vibration Analysis of a Beam with Axial Variation of Material Properties

Abstract

The study examines the vibration analysis of a damped cantilever beam with nonuniform variation in material properties using finite element methods. With power modification of material parameters in the axial direction, the static and dynamic response of a prismatic rectangular beam with damping has been examined. For the finite element approach, two noded beam elements with two degrees of freedom at each node were evaluated. The power law variation of material properties was used throughout the investigation. This research investigated the effects of proportional damping on displacement, velocity, and acceleration responses. The proposed beam\'s mass, stiffness, and damping matrices were calculated using Hamilton\'s concept. In the temporal domain, the Newmark Method has been utilized.

Introduction

I. INTRODUCTION

Nowadays, functionally graded (FG) materials are regarded as among the most advanced materials, with mechanical properties that gradually vary with respect to a chosen spatial coordinate. In comparison to laminated composites, using FG materials in structural systems eliminates stress concentration and enhances the structure's strength and toughness. Most of the literature on FG beams deals with beams whose mechanical properties vary through thickness[1][2][3].There are relatively few works on axially FG beams whose mechanical properties vary along the axis of the beam where most of them concern the special case of uniform beams. Due to varying cross-sectional area, modulus of elasticity and mass density along the beam axis, the governing differential equations of axially FG tapered beams for transverse and longitudinal vibrations and buckling are differential equations with variable coefficients for which closed-form solutions could be hardly found or even impossible to obtain; hence application of numerical techniques is essential. FEM has been used to study the free vibration of an AFG-tapered beam based on Euler-Bernoulli and Timoshenko beam theory[4][5].The free vibration analysis of AFG-tapered Euler-Bernoulli beams employing the differential transform element method has been studied[6].The free bending vibration of rotating AFG-tapered Euler-Bernoulli beams with different boundary conditions using the differential transformation method and differential quadrature element method[7].Further, the free vibration analysis of AFG Timoshenko beams using the same method has been studied [8].The free vibration of variable cross-sectional axially functionally graded beam has been studied [9].The differential equation with variable coefficients is combined with the boundary conditions and transformed into Fredholm integral equation. By solving Fredholm integral equation, the natural frequencies of axially functionally graded beams can be obtained. The free vibration analysis of a functionally graded ordinary (FGO) twisted Timoshenko beam of cantilever type was investigated. The shape functions were derived from differential equations of static equilibrium. The mass and stiffness matrices were obtained from the energy equation. The various material properties along the thickness direction are assumed to vary according to a power law. It was observed from the analysis that increasing the pretwist angle, the first natural frequency increased whereas the second natural frequency decreased. The simultaneous effects of power law index and pretwist angle on first natural frequency were conducted and observed that it was marginal[10].The bending analysis of a simply supported FG beam subjected to uniformly distributed load (UDL) was investigated. The material properties of the FG beam varied continuously in the thickness direction based on power law. The position of the natural surface of the FG beam was obtained, and its influence on the deflection of the beam under UDL was studied[11].The numerical calculations for natural frequencies of FG simply supported beams were presented. The first order Timoshenko beam theory and third-order shear deformation theory were applied for the analysis of FG beam. The nonlinear forced vibration analysis of a beam made of FG material was presented.

The modelling of the beam was carried out using Euler-Bernoulli beam theory and von Karman geometric nonlinearity. The effects of material properties on the nonlinear dynamic behavior of FG beam were discussed. The frequency response equation of the system was presented, and the effects of different parameters on the response of the system were investigated[12].The free vibration analysis of a functionally graded ordinary (FGO) twisted Timoshenko beam of cantilever type was investigated. The shape functions were derived from differential equations of static equilibrium. The mass and stiffness matrices were obtained from the energy equation. The various material properties along the thickness direction are assumed to vary according to a power law. It was observed from the analysis that increasing the pretwist angle, the first natural frequency increased whereas the second natural frequency decreased. The simultaneous effects of power law index and pretwist angle on first natural frequency were conducted and observed that it was marginal. The bending analysis of a simply supported FG beam subjected to uniformly distributed load (UDL) was investigated. The material properties of the FG beam varied continuously in the thickness direction based on power law. The position of the natural surface of the FG beam was obtained, and its influence on the deflection of the beam under UDL was studied. The bending analysis of a simply supported FG beam subjected to uniformly distributed load (UDL) was investigated. The material properties of the FG beam varied continuously in the thickness direction based on power law. The position of the natural surface of the FG beam was obtained, and its influence on the deflection of the beam under UDL was studied[13].The free vibration analysis of a simply supported FG beam with piezoelectric layers subjected to axial compressive loads was studied. The various effects of volume fractions, the effects of applied voltage and axial compressive loads on the vibration frequency were presented. It was concluded from the analysis that the piezoelectric actuators induce tensile piezoelectric force produced by applying negative voltages that significantly affect the free vibration of the FG beam. The vibration frequency increases when the applied voltage is negative[14].The differential transformation method (DTM) was applied for investigating the free vibration analysis of FG beams with arbitrary boundary conditions, including various types of elastically end constraints. By using DTM, the natural frequencies and mode shapes were presented. For free vibration of the beam, Al2O3/Al was considered for the study. It was seen that there was considerable variation of frequencies and mode shapes when the stiffness of spring becomes more[15].A new approach has been initiated based on Chebyshev polynomial theory to investigate the free vibration of AFG Euler-Bernoulli and Timoshenko beams with nonuniform cross sections[16].Even though several research works has been commenced on axial functionally graded beam still there is some gap in the vibration analysis of beams with variation of material properties in axial direction through finite element method. The present paper is an initiation towards the analysis of static and dynamic response of such beam with proposed power law variation of material properties in axial direction. The material properties are an essential aspect in design consideration of any beam, which need an attention for study. The behaviour of such beam has been analysed in Matlab environment.

II. MATHEMATICAL MODELLING OF THE PROPOSED  BEAM

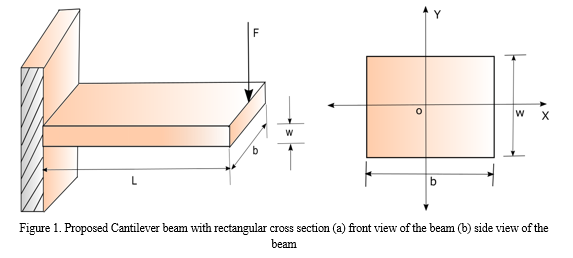
The theory of beam and mathematical formulations involve the modeling of beam with finite element analysis (FEA) from vibrating of such beam. The detail of the above formulation is presented in the following subsections. A cantilever beam is shown Figure 1 for dynamic analysis when subjected to an impulse force.

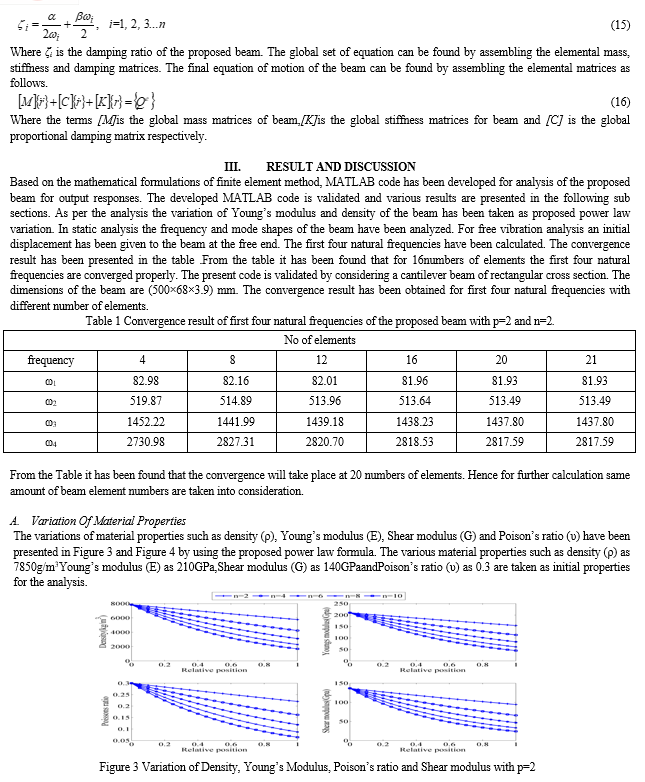
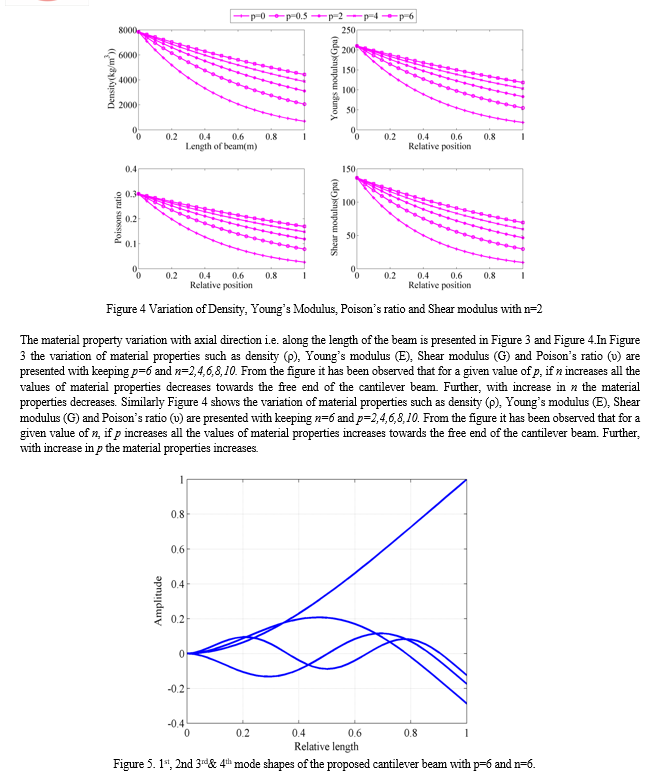
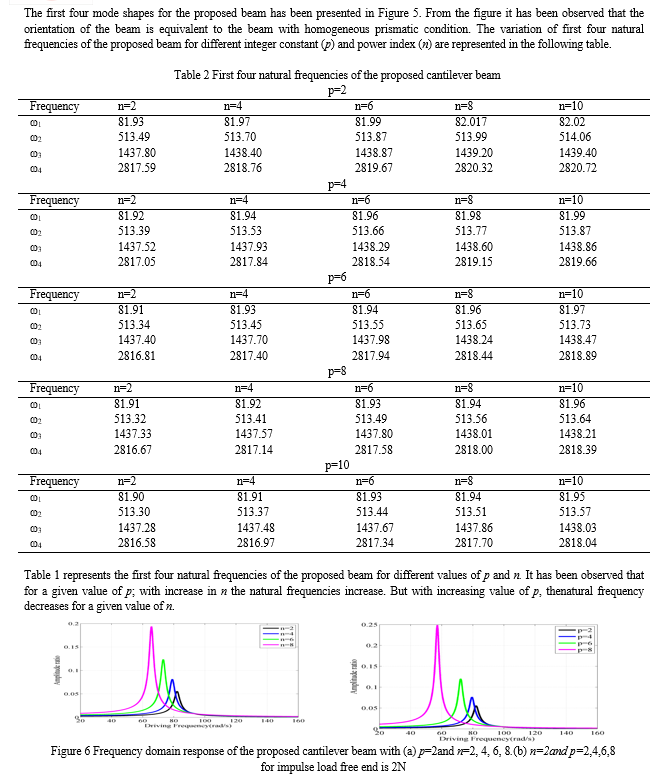
The frequency domain analysis of the proposed beam for p=2 and four different values of n such as 2, 4, 6 and 8has been carried out. The dynamic responses have been carried out with an impulse load of 2 N. The obtained response is shown in Figure 6 Frequency domain response of the proposed cantilever beam with (a) p=2and n=2, 4, 6, 8.Figure 6(a). From the figure it has been observed that the peak response of the proposed beam increases as the power gradient index increases. It has been observed further that there is 68% increase of amplitude as the value increases from 2 to 8. This is due to the fact that with increase in power gradient index the amount of damping decreases. Further, it has been perceived that the resonant frequency of the proposed beam decreases as the value of n increases. This is due to the fact that as the value of n changes, there is a variation in material properties which affects both the stiffness and mass matrices of the beam. Similarly, the frequency domain analysis has been carried out for n=2 and four different values of p such as 2, 4, 6 and 8. The response of such beam is shown in Figure 6(b).From the figure it has been observed that with increase in the value of p there is an increase in amplitude of the proposed beam for a given value of n. It has been noticed that there is an increase in 80% of amplitude when the value of p changes from 2 to 8. This is due to the fact that the amount of damping decreases when the value of p increases. Further, the increase in amplitude is more for the beam when compared with the previous case. Moreover, the resonant frequency is also decreases asthe value of p increases. The value of damping is more with increase in k as compared to increase in n.

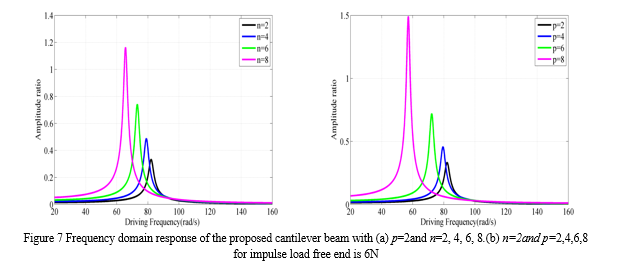
The frequency domain analysis of the proposed beam for p=2 and four different values of n such as 2, 4, 6 and 8 has been carried out. The dynamic responses have been carried out with an impulse load of 6 N. The obtained response is shown in Figure 6 Frequency domain response of the proposed cantilever beam with (a) p=2and n=2, 4, 6, 8.Figure 7(a). From the figure it has been observed that the peak response of the proposed beam increases as the power gradient index (n) increases. It has been observed further that there is 76% increase of amplitude as the value increases from 2 to 8. This is due to the fact that with increase in power gradient index the amount of damping decreases. Further, it has been perceived that the resonant frequency of the proposed beam decreases as the value of n increases. This is due to the fact that as the value of n changes, there is a variation in material properties which affects both the stiffness and mass matrices of the beam. Similarly, the frequency domain analysis has been carried out for n=2 and four different values of p such as 2, 4, 6 and 8. The response of such beam is shown in Figure 7(b).From the figure it has been observed that with increase in the value of p there is an increase in amplitude of the proposed beam for a given value of n. It has been noticed that there is an increase in 76% of amplitude when the value of p changes from 2 to 8. This is due to the fact that the amount of damping decreases when the value of p increases. Further, the increase in amplitude is more for the beam when compared with the previous case. Moreover, the resonant frequency is also decreases as the value of p increases. The value of damping is more with increase in k as compared to increase in n. Further from Figure 6 and Figure 7 it has been found that as the impulse force increases from 2N to 6 N the resonant frequency amplitude increases to 83% for both p=2; n=8 and n=2; p=8 case. This is due to the fact that as the impulse force increases the damping factor of the beam decreases which results in increase in amplitude.

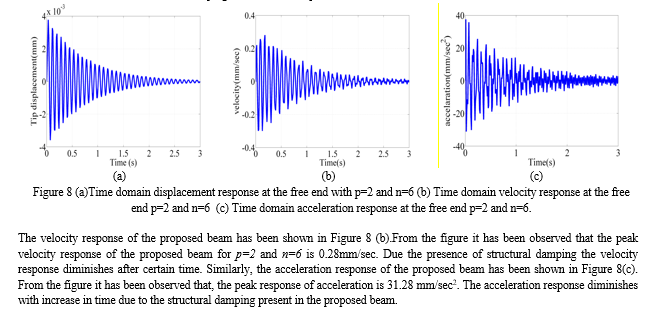
The time domain analysis has been carried out using Newmark method in Matlab environment with 2N impulse load at the free end of the proposed cantilever beam.

The time domain responses such as displacement, velocity and acceleration have been carried out for 3 sec. The amount of proportional damping has been taken into account in the analysis. The responses have been shown in Figure 8 (a-c). From the figure it has been observed that the peak response of the beam is 3.8mm. The tip displacement response goes on decreasing with increasing in time. This is due to the structural damping for which the response diminishes with increase in time.

Conclusion

The present paper uses the finite element approach to analyse the static and dynamic vibrations of a cantilever prismatic beam with nonuniform variation of material properties in the axial direction. For the analysis, a hypothesized power variation of material attributes was used. In order to solve the governing equation, two noded beam elements with two degrees of freedom at each node are examined. The Euler-Bernoulli beam theory was investigated for solving the beam\'s governing equation. It has been discovered that material qualities play an important role in beam vibration analysis. It has been noticed that as the power gradient index grows, the amplitude of vibration increases while the fundamental frequency falls. It has once again been determined that structural dampening has a role.

References

[1] L.-L. Ke, J. Yang, S. Kitipornchai, and Y. Xiang, “Flexural vibration and elastic buckling of a cracked Timoshenko beam made of functionally graded materials,” Mech. Adv. Mater. Struct., vol. 16, no. 6, pp. 488–502, 2009. [2] M. A. Benatta, A. Tounsi, I. Mechab, and M. B. Bouiadjra, “Mathematical solution for bending of short hybrid composite beams with variable fibers spacing,” Appl. Math. Comput., vol. 212, no. 2, pp. 337–348, 2009. [3] S. A. Sina, H. M. Navazi, and H. Haddadpour, “An analytical method for free vibration analysis of functionally graded beams,” Mater. Des., vol. 30, no. 3, pp. 741–747, 2009. [4] A. Shahba, R. Attarnejad, and S. Hajilar, “Free vibration and stability of axially functionally graded tapered Euler-Bernoulli beams,” Shock Vib., vol. 18, no. 5, pp. 683–696, 2011. [5] A. Shahba and S. Rajasekaran, “Free vibration and stability of tapered Euler–Bernoulli beams made of axially functionally graded materials,” Appl. Math. Model., vol. 36, no. 7, pp. 3094–3111, 2012. [6] A. Shahba, R. Attarnejad, M. T. Marvi, and S. Hajilar, “Free vibration and stability analysis of axially functionally graded tapered Timoshenko beams with classical and non-classical boundary conditions,” Compos. Part B Eng., vol. 42, no. 4, pp. 801–808, 2011. [7] S. Rajasekaran, “Differential transformation and differential quadrature methods for centrifugally stiffened axially functionally graded tapered beams,” Int. J. Mech. Sci., vol. 74, pp. 15–31, 2013. [8] S. Rajasekaran and E. Norouzzadeh Tochaei, “Free vibration analysis of axially functionally graded tapered Timoshenko beams using differential transformation element method and differential quadrature element method of lowest-order,” Meccanica, vol. 49, no. 4, pp. 995–1009, 2014. [9] Y. Huang and X.-F. Li, “A new approach for free vibration of axially functionally graded beams with non-uniform cross-section,” J. Sound Vib., vol. 329, no. 11, pp. 2291–2303, 2010. [10] S. C. Mohanty, “Free vibration analysis of a pretwisted functionally graded material cantilever Timoshenko beam,” 2012. [11] H. Yaghoobi and A. Fereidoon, “Influence of neutral surface position on deflection of functionally graded beam under uniformly distributed load,” World Appl. Sci. J., vol. 10, no. 3, pp. 337–341, 2010. [12] M. Rafiee, H. Kalhori, and S. Mareishi, “Nonlinear resonance analysis of clamped functionally graded beams,” 2011. [13] G. R. Koochaki, “Free vibration analysis of functionally graded beams,” World Acad. Sci. Eng. Technol., vol. 74, 2011. [14] M. Karami Khorramabadi, “Free vibration of functionally graded beams with piezoelectric layers subjected to axial load,” J. Solid Mech., vol. 1, no. 1, pp. 22–28, 2009. [15] N. Wattanasakulpong and V. Ungbhakorn, “Free vibration analysis of functionally graded beams with general elastically end constraints by DTM,” World J. Mech., vol. 2, no. 06, p. 297, 2012. [16] A. E. Alshorbagy, M. A. Eltaher, and F. Mahmoud, “Free vibration characteristics of a functionally graded beam by finite element method,” Appl. Math. Model., vol. 35, no. 1, pp. 412–425, 2011. [17] A. R. Biswal, T. Roy, and R. K. Behera, “Optimal vibration energy harvesting from non-prismatic axially functionally graded piezolaminated cantilever beam using genetic algorithm,” J. Intell. Mater. Syst. Struct., vol. 28, no. 14, pp. 1957–1976, 2017. [18] A. R. Biswal, T. Roy, and R. Kumar Behera, “Geometric nonlinear finite element and genetic algorithm based optimal vibration energy harvesting from nonprismatic axially functionally graded piezolaminated beam,” J. Vib. Control, vol. 24, no. 10, pp. 1889–1909, 2018.

Copyright

Copyright © 2023 Alok Ranjan Biswal, Deepak Ranjan Biswal, Rasmi Ranjan Senapati, Abinash Bibek Dash, Poonam Prusty, Shibabrata Mohapatra, Sanjeev Panda. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.