Implementation of 2-bit Multiplier Circuit Using Pass Transistor Logic

Abstract

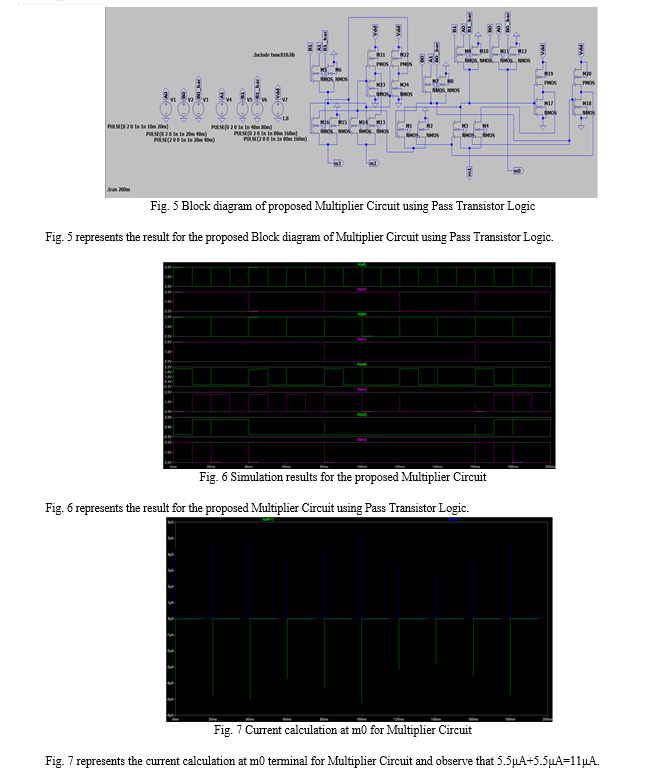
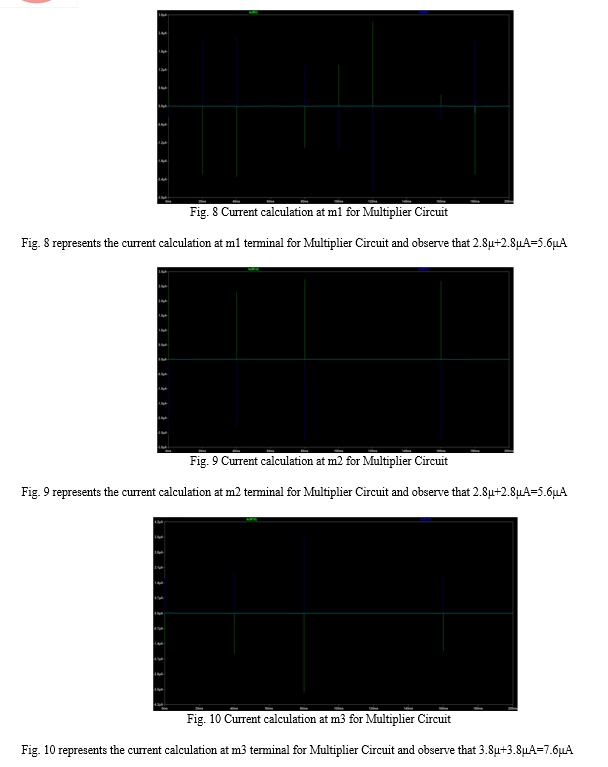
In this paper, we implemented 2-bit Multiplier Circuit using Pass Transistor Logic. Pass Transistor Logic is used for high speed technology and is easy to build the basic gate structures. The developed circuit is an extension of pass transistor logic Ex-or gate. The proposed Multiplier circuit is implemented in 2x2 bit multiplier to achieve high speed, low area and less power dissipation. VLSI schematic tool and the analysis is done by using the LT Spice simulator. This paper aims at an optimization of power area and voltages of multiplier to show the better performance. The design is implemented in 0.18um CMOS technology and its functional parameters are compared and the best result is incorporated. Simulation results have been performed on LT Spice tool simulator at 1.8v and 2v supply voltage and simulations are carried out indicate the functionality of the proposed multiplier circuit compared with conventional design to verify the effectiveness and it shows the circuit has low power dissipation at high speeds.

Introduction

I. INTRODUCTION

A binary multiplier is an electronic circuit used in digital electronics, such as a computer, to multiply two binary numbers. A variety of computer arithmetic techniques can be used to implement a digital multiplier. Most techniques involve computing the set of partial products, which are then summed together using binary adders. This process is similar to long multiplication, except that it uses a base-2 (binary) numeral system.

A. Binary Long Multiplication

The method taught in school for multiplying decimal numbers is based on calculating partial products, shifting them to the left and then adding them together. The most difficult part is to obtain the partial products, as that involves multiplying a long number by one digit (from 0 to 9). A binary computer does exactly the same multiplication as decimal numbers do, but with binary numbers. In binary encoding each long number is multiplied by one digit (either 0 or 1), and that is much easier than in decimal, as the product by 0 or 1 is just 0 or the same number. Therefore, the multiplication of two binary numbers comes down to calculating partial products (which are 0 or the first number), shifting them left, and then adding them together (a binary addition, of course):

This is much simpler than in the decimal system, as there is no table of multiplication to remember: just shifts and adds. This method is mathematically correct and has the advantage that a small CPU may perform the multiplication by using the shift and add features of its arithmetic logic unit rather than a specialized circuit. The method is slow, however, as it involves many intermediate additions. These additions are time-consuming. Faster multipliers may be engineered in order to do fewer additions; a modern processor can multiply two 64-bit numbers with 6 additions (rather than 64), and can do several steps in parallel.

A multiplier is a combinational logic circuit that we use to multiply binary digits. Just like the adder and the subtractor, a multiplier is an arithmetic combinational logic circuit. It is also known as a binary multiplier or a digital multiplier.

Where is the use of a multiplier?We use a multiplier in several digital signal processing applications. We use it to design calculators, mobiles, processors, and digital image processors.

How does binary multiplication work and how to design a 2-bit multiplier?

Binary multiplication works just like normal multiplication. There are four main rules that are quite simple to understand:

0  x  0  =  0

0  x  1  =  0

1  x  0  =  0

1  x  1  =  1

Suppose you have two binary digits A1A0 and B1B0, here’s how that multiplication would take place.

II. LITERATURE SURVEY

Literature survey is done on some papers firstly “A robust asynchronous 16×16-bit sub threshold multiplier using SAPTL Technique” [1] occupies more number of transistors hence there is a requirement of area optimization for the multiplier circuit. And another work is Systematic synthesis of approximate adders and multipliers with accurate error calculations [2]. Using this technology there is a need of power optimization in the design. A Hybrid 4-bit Radix-4 Low Power Booth Multiplier with High Performance [3]. No exact truth table simulation results observed in that work there is a need of timing analysis in the work. Another work ASIC Design of Reversible Multiplier Circuit [4] transistors used in the work is more hence there is a requirement of area optimization. Compressor Using Full Swing XOR Logic Gate [5]. In this work some glitches are observed in Output simulations and noise removal is required. In Design and Analysis of Approximate Multipliers For Error-Tolerant Applications [6] and in Design and Analysis of Wallace Tree Multiplier for CMOS and CPL Logic [7]  and in Design of Low Power and Energy Efficient 5 X 5 Multipliers [8] needed Power dissipation to optimize.

Design of Low-Power and High Performance Radix-4 Multiplier [9] no simulation results are observed. In Design of Power Efficient Vedic Multiplier using Adiabatic Logic [10] glitches are observed in simulation results. In Low-Cost Design of Serial-Parallel Multipliers Over GF(2m) Using Hybrid Pass-Transistor Logic (PTL) and CMOS Logic [11] optimization of power is still needed. Modified Mac Unit for Low Power High Speed Dsp Application Using Multipler with Bypassing Technique and Optimized Adders [12] occupies more number of transistors hence there is a requirement of area optimization for the multiplier circuit

An ultra-low power multiplier using multi-valued adiabatic logic in 65?nm CMOS process [14] observed the circuit is complex and also having some glitches in the simulations results.

Hence there is a need of the multiplier circuit with less number of transistors occupies less space and fast operation and less power dissipation.

III. IMPLEMENTATION

A. Pass Transistor Logic

Pass transistor logic (PTL) in electronics refers to several logic families used in the design of integrated circuits. It reduces the number of transistors used to construct various logic gates by eliminating redundant transistors. Instead of being connected directly to supply voltages, transistors are used as switches to pass logic levels between nodes in a circuit. This reduces the number of active devices but has the disadvantage of decreasing the voltage difference between high and low logic levels at each stage. Each transistor in series has a lower saturation at its output than it does at its input. If several devices in a logic path are chained in series, a conventionally constructed gate may be required to restore the signal voltage to its full value. Conventional CMOS logic, on the other hand, switches transistors so that the output connects to one of the power supply rails (similar to an open collector scheme), so logic voltage levels in a sequential chain do not decrease. Circuit simulation may be required to ensure adequate performance.

B. Applications

Pass transistor logic frequently uses fewer transistors, runs faster, and consumes less power than fully complementary CMOS logic implementing the same function with the same transistors. If implemented with simple gates, XOR has the worst-case Karnaugh map and requires the most transistors of any function. By implementing the XOR using pass-transistor logic rather than simple gates, the designers of the Z80 and many other chips saved a few transistors.

???????C. Basic principles of pass transistor circuits

A periodic clock signal drives the pass transistor, which acts as an access switch to charge up or charge down the parasitic capacitance Cx depending on the input signal Vin. When the clock signal is active (CK = 1), the two possible operations are the logic "1" transfer (charging up the capacitance Cx to a logic-high level) and the logic "0" transfer (charging down the capacitance Cx to a logic-low level). Depending on the voltage Vx, the output of the depletion load nMOS inverter obviously assumes a logic-low or logic-high level.

???????D. Complementary pass transistor logic

Some authors use the phrase "complementary pass transistor logic" to describe a method of implementing logic gates that employs transmission gates made up of both NMOS and PMOS pass transistors. Other authors use the term "complementary pass transistor logic" (CPL) to describe a method of implementing logic gates that includes an NMOS-only pass transistor network followed by a CMOS output inverter.

Other authors refer to "complementary pass transistor logic" (CPL) as a method of implementing logic gates that uses dual-rail encoding. Every CPL gate has two output wires, one for the positive signal and the other for the complementary signal, which eliminates the need for inverters.

Complementary pass transistor logic, also known as "Differential pass transistor logic," is a logic family that is designed for a specific advantage. This logic family is commonly used for multiplexers and latches.

CPL employs series transistors to select between the logic's possible inverted output values, the output of which drives an inverter. The CMOS transmission gates are made up of parallel nMOS and pMOS transistors.

???????E. Other Forms

There are static and dynamic types of pass transistor logic, with different properties in terms of speed, power, and low-voltage operation. The disadvantages of pass transistor logic become more apparent as integrated circuit supply voltages decrease; the threshold voltage of transistors becomes large in comparison to the supply voltage, severely limiting the number of sequential stages. Additional logic stages are required because complementary inputs are frequently required to control pass transistors.

In the above calculation, A1A0 is the multiplicand. B1B0 is the multiplier. The first product obtained from multiplying B0 with the multiplicand is called as partial product 1. And the second product obtained from multiplying B1 with the multiplicand is known as the partial product 2.

As the number of bits increases, we keep shifting each successive partial product to the left by 1 bit. In the end, we add the digits while keeping in mind the carry that might generate.

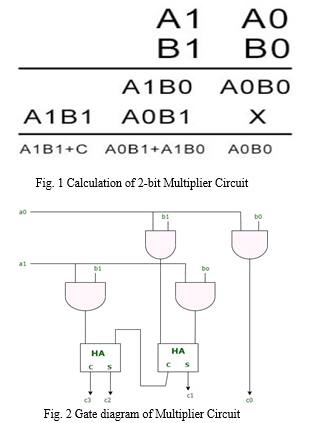
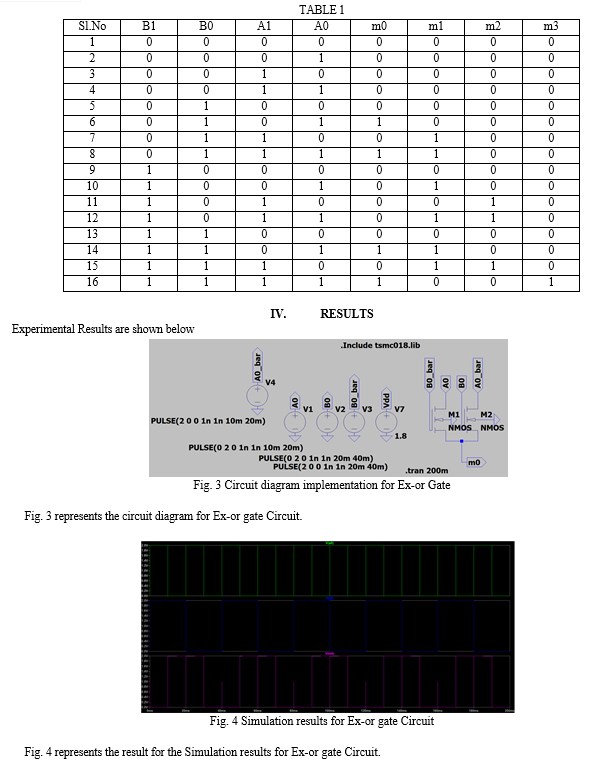
Based on the above equation, we can see that we need four AND gates and two half adders to design the combinational circuit for the multiplier. The AND gates will perform the multiplication, and the half adders will add the partial product terms. Hence the circuit obtained. Fig. 1 shows the calculation of 2-bit Multiplier circuit and Fig. 2 shows the Gate diagram of Multiplier Circuit and Table 1 is represented as truth table for the proposed circuit.

???????

Conclusion

This paper provided a brief explanation of the design of a two-bit multiplier circuit using pass transistor logic. And the simulation results validated its functionality. By maximizing, the output voltage values of m0, m1, m2, and m3 can be reduced to logic values of other signals. The implemented circuits have a simpler design and are expected to perform better and consume less power than the existing full adder circuit models. Our proposed design has demonstrated a significant improvement in area, voltages, current, and power, and further improvements can be made to reduce these as well. Whereas the existing adders exhibit very little distortion. The implemented design is used for future analysis as well as 4-bit and 8-bit design Multiplier, however, the goal of this implementation is used to design the sub-blocks in ALU.

References

[1] Qi Zhang, Yuping Wu, Lan Chena, and Xuelian Zhang, “A robust asynchronous 16×16-bit subthreshold multiplier using SAPTL Technique [2]”, Microelectronics Reliability 91 (2018) 98–111, 31 August 2018, pp 98-111. [2] Saurabh Katariya and Manish Singhal “A Hybrid 4-bit Radix-4 Low Power Booth Multiplier With High Performance [4]”, IEEE International Conference on Recent Advances and Innovation in Engineering (ICRAIE -2016), Dec- 23- 25, 2016, Jaipur, India. [3] Hatkar A. P., Hatkar A. A. and Narkhede N. P, “ASIC Design of Reversible Multiplier Circuit [5]”, 2014 International Conference on Electronic Systems, Signal Processing and Computing Technologies, pp 48-52. [4] Sri Harsha Bandarupalli, Bala Pavan Kalyan Bandi, Rahul Kumar Reddy Boggula, Kirti S. Pande, “Compressor Using Full Swing XOR Logic Gate [6]”, IEEE, pp84-89. [5] Anirudha Pandey, Manikantta Reddy K., Praveen Yadav, Nithin Kumar Y.B., Vasantha M.H, “Design and Analysis of Approximate Multipliers For Error-Tolerant Applications [7]”, 2018 IEEE International Symposium on Smart Electronic Systems (iSES), pp-94-97. [6] S.Nagaraj, K.Thyagarajan , D.Srihari K.Gopi , “Design and Analysis of Wallace Tree Multiplier for CMOS and CPL Logic [8]”, 2018 INTERNATIONAL CONFERENCE ON COMPUTATION OF POWER, ENERGY, INFORMATION AND COMMUNICATION (ICCPEIC), pp-6-10. [7] Ajeya Vallamdas , Arunkumar P Chavan , SJagannathan “Design Of Low Power And Energy Efficient 5 X 5 Multipliers [9]”, IEEE International Conference on Recent Advances and Innovations in Engineering (ICRAIE-2014), May 09-11, 2014, Jaipur, India. [8] lackuline Moni D, Anu Priyadharsini K , “DESIGN Of LOW-POWER AND HIGH PERFORMANCE RADIX-4 MULTIPLIER [10]”, [9] Kuheli Dutta, Sudipta Chattopadhyay , Vaishna Biswas and Suman Roy Ghatak “Design of Power Efficient Vedic Multiplier using Adiabatic Logic [11]”, IEEE, PP-1-6. [10] Pramod Kumar Meher and Shen-Fu Hsiao, Chia-Sheng Wen and Ming-Yu Tsai “Low-Cost Design of Serial-Parallel Multipliers Over GF(2m) Using Hybrid Pass-Transistor Logic (PTL) and CMOS Logic [12]”, 2010 International Symposium on Electronic System Design, pp 132-134. [11] Teffi Francis , Tresa Joseph Jobin and K Antony, “Modified Mac Unit For Low Power High Speed Dsp Application Using Multipler With Bypassing Technique And Optimized Adders [13]”, IEEE, 4th ICCCNT – 2013. [12] ZhangYuejunaDingDailuaPanZhaoaWangPengjunabYuQiaoyan “An ultra-low power multiplier using multi-valued adiabatic logic in 65?nm CMOS process [14]”, Microelectronics Journal, Volume 78, August 2018, Pages 26-34.

Copyright

Copyright © 2022 Panchadi Swathi, Gudla Bhanu Gupta. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.