The Study on the Nonlinear Effects of Soliton in Optical Fibre

Abstract

In optical fibres, the chirps generated by GVD and SPM, which both limit the system\'s performance when operating independently, balance each other out to produce soliton formation. To comprehend how such a balance is possible, we shall study the nonlinear optical effects and the dispersion-induced pulse broadening. If an optical pulse is not adequately chirped before it propagates inside an optical fibre, the GVD broadens the pulse. More specifically, an early stage of transmission compresses a chirped pulse whenever ?2 and the chirp parameter C have opposite signs and ?2C is negative. The optical pulse chirps due to SPM, ensuring that C > 0. If ?2 < 0, it is easy to meet the criteria ?2C < 0. Moreover, because the SPM-induced chirp depends on power, it is possible that in some situations, SPM and GVD could cooperate to the extent that the SPM-induced chirp is precisely the right amount to cancel out the pulse broadening caused by GVD. Here, an optical pulse propagates distortion-free as a soliton [27].

Introduction

I. INTRODUCTION

It is challenging to define soliton in a way that is widely accepted. Three features are offered to soliton by Drazin & Johnson (1989, p. 15). [1]. They can communicate with other solitons, have a permanent shape, and are restricted to a specific area. They do not get affected by collisions other than avoiding phase transitions.There are more formal formulas available, albeit they require a great deal of mathematics. Furthermore, certain scientific occurrences that fail to satisfy these three conditions are classified as soliton phenomena (for example, even though they lose energy during interaction, solitons are sometimes used to characterise "light bullets" in nonlinear optics).[2] Wave patterns can be either permanent or limited, depending on the interplay between dispersion and nonlinearity. Envision a brilliant pulse passing through a piece of glass. This pulse might be made up of several different light frequencies. These different frequencies propagate through glass at different speeds due to its dispersion, which gradually modifies the pulse's structure. There is also the nonlinear Kerr effect, which asserts that the brightness or amplitude of the light determines a material's refractive index at a specific frequency. Because the Kerr effect precisely cancels the dispersion effect, a properly created pulse maintains its shape throughout time. The pulse is a soliton as a result [3]. Solitons can completely solve a number of nonlinear Schrödinger equations, the coupled nonlinear Schrödinger equation, the sine-Gordon equation, the Korteweg–de Vries equation, and other models. The soliton solutions are stable because the field equations are integrable, which is usually achieved using the inverse scattering transform. One vibrant and expansive area of mathematics is the mathematical theory of these equations.[3] A train of solitons moves concurrently with a wavefront in some undular tidal bore events that occur in a few rivers, such the River Severn. As internal waves travel down the oceanic pycnocline, propelled by the seafloor's topography, more solitons are created. Soliton counts in the atmosphere are higher. Consider the morning beauty cloud in the Gulf of Carpentaria as an illustration. It is produced by massive linear roll clouds caused by pressure solitons travelling across a temperature inversion layer. The signal conduction within neurons is described by pressure solitons in the recently suggested, but not widely accepted, neuroscience soliton model [3].Any solution of a system of partial differential equations that is persistent against decay to the "trivial solution" is referred to as a topological soliton, also known as a topological defect. The origin of soliton stability is not the integrability of the field equations, but topological constraints. Due to the differential equations' need to uphold the boundary's nontrivial homotopy group and adhere to a set of boundary conditions, constraints are nearly always present. Therefore, solutions to differential equations can be arranged using homotopy classes [3].

More precisely, soliton transmission in optical fibres enhances data transmission quality by mitigating two main forms of pulse degradation. The dispersion that occurs when pulses travel across extended fibre lengths is one kind of degradation. The other is the nonlinear effects resulting from signals interacting with the fibre and with each other in a power-dependent manner. Nonetheless, the effects can cancel each other out, at least to first-order approximation, for certain types and powers of optical pulses.

In general, the two effects exacerbate one another and worsen the illness. These pulse forms are called soliton pulses.One of the key benefits of soliton gearboxes for high-speed, long-distance applications is their inherent endurance. Despite soliton attenuation, soliton can be made fundamentally stable over long fibre lengths. This provides a means of mitigating the significant loss of signal quality at 10 Gbit/s and greater transmission speeds caused by dispersion and nonlinear effects. Because of these characteristics, researchers are creating soliton systems for upcoming 40-Gbit/s and long-haul 10-Gbit/s networks [4].

II. LITERATURE REVIEW

When John Scott Russell (1808–1882) observed a single wave on Scotland's Union Canal in 1834, he became the first person to record the soliton phenomenon. He called the phenomenon the "Wave of Translation" after he was able to reproduce it in a wave tank. Solutions to the Korteweg–de Vries equation that propagate locally limited and strongly stable can describe waves comparable to the ones Russell observed. Zabusky and Kruskal originally gave these solutions the name "soliton." With the suffix "on" evoking its historical use to identify particles like hadrons, baryons, and electrons and noting their observed particle-like activity, the term was intended to emphasise the solitary nature of the waves[3].

A young engineer named John Scott Russell, engaged for a summer project in 1834 to look at ways to enhance the designs for barges intended to cross canals specifically, the Union Canal in Edinburgh, Scotland—made the first known observation of a lone wave. The barge came to a startling stop one August day when the tow line that held the mules in place broke. However, the body of water ahead of the blunt prow of the barge rolled rapidly, forming a large, solitary elevation and a smooth, rounded mound of water that continued down the canal at the same direction and speed. Russell (1844). Russell rode up to and passed the Wave of Translation as a follow-up to this unintentional discovery. Equation (1) illustrates how the amplitude effect, a nonlinear component, and the dispersive termwhich permits waves of various wavelengths to travel at different velocities—combine to determine the rate of change of the wave's height over time. Korteweg and de Vries discovered a periodic solution that matched Russell's wave in addition to a solitary-wave solution. A trade-off between dispersion and nonlinearity led to these solutions. Mathematicians, physicists, and engineers researching water waves disregarded Russell's findings and the work of Norman Zabusky and Martin Kruskal, who published their numerical solutions to the KdV equation (and coined the term "soliton"), until 1965 (Zabusky, 1965). Kruskal generated a continuous description of the oscillations of unidirectional waves propagating on the cubic, Fermi–Pasta–Ulam (FPU) nonlinear lattice, according to (1) (Fermi, 1955; Porter, 2009b; Weissert, 1997). Morikazu Toda made history at the same time when he identified a soliton for the first time in the discrete, integrable system that is now known as the Toda lattice and Toda, 1967.[5]

Films of interacting solitary waves in an FPU lattice, the KdV equation, and a modified KdV equation were created by Gary Deem, Zabusky, and Kruskal (1965); refer to the discussion in the review paper (Zabusky, 1984). We illustrate the dynamics of solitons in the space-time diagram shown in Figure 1 using the KdV equation. Robert Miura discovered a precise transition between this modified KdV equation and equation (1) when he understood the significance of this discovery (Miura, 1976). There was a spike in interest in the mathematical study of solitons following the 1967 solution of the initial-value problem of the KdV equation by Clifford Gardner, John Greene, Martin Kruskal, and Robert Miura (Miura, 1968; Gardner, 1967; Gardner, 1974).  By demonstrating the integrability of the nonlinear Schrödinger (NLS) problem and the availability of soliton solutions, Vladimir Zakharov and Alexei Borisovich Shabat expanded the use of the inverse scattering approach in 1972. One of the several nonlinear PDEs for which Mark Ablowitz, David Kaup, Alan Newell, and Harvey Segur demonstrated that they had soliton solutions in 1973 was the sine-Gordon equation. Albert Backlünd's 19th-century work on surfaces with continuous negative Gaussian curvature established the integrability of this equation. Since then, researchers in one or more spatial dimensions have looked into related soliton solutions and have discovered alternative integrable PDEs.

A more sophisticated definition of a "soliton" over many spatial dimensions is required, as the Kadomtsev-Petviashvili (KP) equation shows.

Analytical approaches for studying solitary waves in nonintegrable equations usually involve the use of asymptotic analysis, variational approximations, and/or perturbative techniques (Kivshar, 1989). (Scott, 2005) The coupled mode equations of the fibre Bragg grating are a well-known illustration of a nonintegrable system having accurate solutions for isolated solitary waves in optics.

One of the most active fields in physics and mathematics today is the study of solitons and solitary waves (Scott, 2005). It has affected several academic disciplines, such as experimental science and pure mathematics. Significant advancements have resulted from this in numerous fields, including supersymmetry, nonlinear dynamics, biology, optics, and integrable systems.

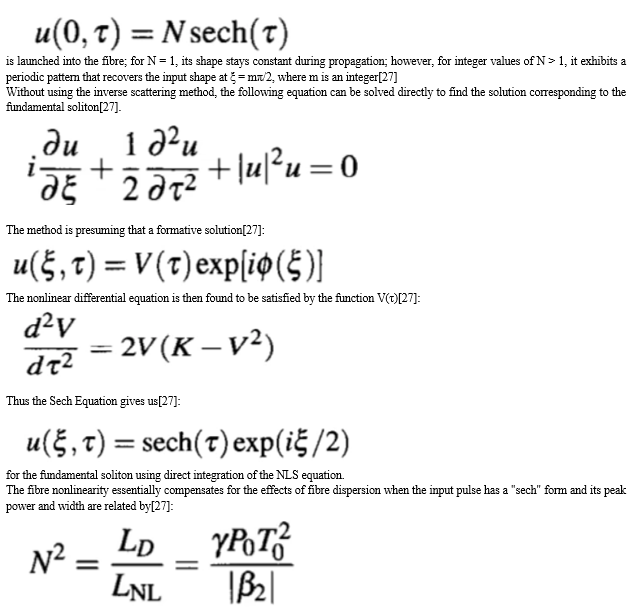
Conclusion

In optical fibres, soliton creation is the result of the mutual balancing of the chirps produced by GVD and SPM, which both reduce the system\'s performance when functioning alone. We will investigate the dispersion-induced pulse broadening and the nonlinear optical effects to understand how such a balance is attainable. The GVD broadens an optical pulse if it is not sufficiently chirped prior to its propagation inside an optical fibre. More precisely, when ?2 and the chirp parameter C have opposite signs and ?2C is negative, an early transmission stage compresses a chirped pulse. SPM causes the optical pulse to chirp, confirming that C > 0. It is simple to achieve the criterion ?2C < 0 if ?2 < 0. Furthermore, because the SPM-induced chirp is power-dependent, it is feasible that under some circumstances, SPM and GVD will work together to the point where the SPM-induced chirp is just the proper amount to cancel out the GVD-caused pulse broadening. Here, a soliton propagates as an optical pulse without distortion.[27]

References

[1] Drazin, P. G.; Johnson, R. S. (1989). Solitons: an introduction (2nd ed.). Cambridge University Press. ISBN 978-0-521-33655-0. [2] https://www.sfu.ca/~renns/lbullets.html#bullets [3] https://en.wikipedia.org/wiki/Soliton#cite_note-2 [4] https://www.laserfocusworld.com/fiber-optics/article/16556409/solitons-balance-signals-for-transmission [5] http://www.scholarpedia.org/article/Soliton [6] G. P. Agrawal, Nonlinear Fiber Optics, (Academic Press, 2007) [7] https://wp.optics.arizona.edu/kkieu/wp-content/uploads/sites/29/2019/04/Solitons-in-optical-fibers-04-05-19.pdf [8] https://www.lightwaveonline.com/optical-tech/transport/article/16647155/future-of-solitons [9] Davydov, Aleksandr S. (1991). Solitons in molecular systems. Mathematics and its applications (Soviet Series). Vol. 61 (2nd ed.). Kluwer Academic Publishers. ISBN 978-0-7923-1029-7. [10] Yakushevich, Ludmila V. (2004). Nonlinear physics of DNA (2nd revised ed.). Wiley-VCH. ISBN 978-3-527-40417-9. [11] Sinkala, Z. (August 2006). \"Soliton/exciton transport in proteins\". J. Theor. Biol. 241 (4): 919–27. Bibcode:2006JThBi.241..919S. CiteSeerX 10.1.1.44.52. doi:10.1016/j.jtbi.2006.01.028. PMID 16516929. [12] Heimburg, T., Jackson, A.D. (12 July 2005). \"On soliton propagation in biomembranes and nerves\". Proc. Natl. Acad. Sci. U.S.A. 102 (2): 9790–5. Bibcode:2005PNAS..102.9790H. doi:10.1073/pnas.0503823102. PMC 1175000. PMID 15994235. [13] Heimburg, T., Jackson, A.D. (2007). \"On the action potential as a propagating density pulse and the role of anesthetics\". Biophys. Rev. Lett. 2: 57–78. arXiv:physics/0610117. Bibcode:2006physics..10117H. doi:10.1142/S179304800700043X. S2CID 1295386. [14] Andersen, S.S.L., Jackson, A.D., Heimburg, T. (2009). \"Towards a thermodynamic theory of nerve pulse propagation\". Prog. Neurobiol. 88 (2): 104–113. doi:10.1016/j.pneurobio.2009.03.002. PMID 19482227. S2CID 2218193.[dead link] [15] Hameroff, Stuart (1987). Ultimate Computing: Biomolecular Consciousness and Nanotechnology. Netherlands: Elsevier Science Publishers B.V. p. 18. ISBN 0-444-70283-0. [16] Weston, Astrid; Castanon, Eli G.; Enaldiev, Vladimir; Ferreira, Fábio; Bhattacharjee, Shubhadeep; Xu, Shuigang; Corte-León, Héctor; Wu, Zefei; Clark, Nicholas; Summerfield, Alex; Hashimoto, Teruo (April 2022). \"Interfacial ferroelectricity in marginally twisted 2D semiconductors\". Nature Nanotechnology. 17 (4): 390–395. arXiv:2108.06489. Bibcode:2022NatNa..17..390W. doi:10.1038/s41565-022-01072-w. ISSN 1748-3395. PMC 9018412. PMID 35210566. [17] Alden, Jonathan S.; Tsen, Adam W.; Huang, Pinshane Y.; Hovden, Robert; Brown, Lola; Park, Jiwoong; Muller, David A.; McEuen, Paul L. (2013-07-09). \"Strain solitons and topological defects in bilayer graphene\". Proceedings of the National Academy of Sciences. 110 (28): 11256–11260. arXiv:1304.7549. Bibcode:2013PNAS..11011256A. doi:10.1073/pnas.1309394110. ISSN 0027-8424. PMC 3710814. PMID 23798395. [18] Zhang, Shuai; Xu, Qiang; Hou, Yuan; Song, Aisheng; Ma, Yuan; Gao, Lei; Zhu, Mengzhen; Ma, Tianbao; Liu, Luqi; Feng, Xi-Qiao; Li, Qunyang (2022-04-21). \"Domino-like stacking order switching in twisted monolayer–multilayer graphene\". Nature Materials. 21 (6): 621–626. Bibcode:2022NatMa..21..621Z.doi:10.1038/s41563-022-01232-2. ISSN 1476-4660. PMID 35449221. S2CID 248303403. [19] Jiang, Lili; Wang, Sheng; Shi, Zhiwen; Jin, Chenhao; Utama, M. Iqbal Bakti; Zhao, Sihan; Shen, Yuen-Ron; Gao, Hong-Jun; Zhang, Guangyu; Wang, Feng (2018-01-22). \"Manipulation of domain-wall solitons in bi- and trilayer graphene\". Nature Nanotechnology. 13 (3): 204–208. Bibcode:2018NatNa..13..204J. doi:10.1038/s41565-017-0042-6. ISSN 1748-3387. PMID 29358639. S2CID 205567456. [20] Nam, Nguyen N. T.; Koshino, Mikito (2020-03-16). \"Erratum: Lattice relaxation and energy band modulation in twisted bilayer graphene [Phys. Rev. B 96 , 075311 (2017)]\". Physical Review B. 101 (9): 099901. Bibcode:2020PhRvB.101i9901N. doi:10.1103/physrevb.101.099901. ISSN 2469-9950. S2CID 216407866. [21] Dai, Shuyang; Xiang, Yang; Srolovitz, David J. (2016-08-22). \"Twisted Bilayer Graphene: Moiré with a Twist\". Nano Letters. 16 (9): 5923–5927. Bibcode:2016NanoL..16.5923D. doi:10.1021/acs.nanolett.6b02870. ISSN 1530-6984. PMID 27533089. [22] Kosevich, A. M.; Gann, V. V.; Zhukov, A. I.; Voronov, V. P. (1998). \"Magnetic soliton motion in a nonuniform magnetic field\". Journal of Experimental and Theoretical Physics. 87 (2): 401–407. Bibcode:1998JETP...87..401K. doi:10.1134/1.558674. S2CID 121609608. Archived from the original on 2018-05-04. Retrieved 2019-01-18. [23] Iwata, Yoritaka; Stevenson, Paul (2019). \"Conditional recovery of time-reversal symmetry in many nucleus systems\". New Journal of Physics. 21 (4): 043010.arXiv:1809.10461. Bibcode:2019NJPh...21d3010I. doi:10.1088/1367-2630/ab0e58. S2CID 55223766. [24] Lightwave, \"Handling Special Effects: Nonlinearity, Chromatic Dispersion, and Soliton Waves,\" July 2000, page 84.) [25] Lightwave, \"Handling Special Effects: Nonlinearity, Chromatic Dispersion, and Soliton Waves,\" July 2000, page 84.) [26] https://www.nakazawa.riec.tohoku.ac.jp/English/reserch/re01.html [27] https://www.fiberoptics4sale.com/blogs/wave-optics/solitons-in-optical-fibers

Copyright

Copyright © 2024 Muhammad Arif Bin Jalil. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.