Ring Oscillator Based True Random Number Generator

Abstract

A true random number generator (TRNG), also known as a hardware random number generator (HRNG), does not use a computer algorithm. Instead, it uses an external unpredictable physical variable such as stochastic models to generate random numbers. Here it gathers data from random electronic signals. Then, the data is converted into digital form and any patterns registered are removed to make it random. This data is used to create random numbers. It is mainly used in Cryptographic Security, authentication, secure communications, e-commerce transactions, Digital Signatures etc. In Existing Method, LFSR based TRNGs generate pseudo random numbers. They produce sequences of bits that appear random but are deterministic and repeat after a certain number of cycles known as the period. They are easy to predict and are not suitable for high security applications. This project aim is to overcome such circumstances, we use TERO(Three Edge Ring Oscillator) based TRNG. Three edges are simultaneously injected by each inverting NAND stage with enable signal Run. These edges will have an identical mean period since they propagate through the same stages. The TERO generates an oscillating signal with a frequency determined by the delay of inverters. TDC (Time to Digital Converter) is used to precisely measure the time intervals between the rising edges of TEROs output signal. Then, it converts time intervals into digital values, effectively generating truly random numbers. Power consumption depends on factors like operating frequency and load capacitance. The Software used is Xilinx Vivado/Xilinx ISE Tools. Here the Proposed Method exquisitely balances Low design effort and resource consumption with high throughput and high randomness.

Introduction

I. INRODUCTION

Random number generators are indispensable components of any modern security system. With physically unclonable functions (PUFs), true random number generators (TRNGs) are the only cryptographic primitives producing truly unpredictable bits for generating secrets in symmetric and public-key cryptography. Random number generators are also extensively used in various randomization-based countermeasures for protecting cryptographic implementations against side-channel attacks (SCA). Among others, the low-latency masking schemes for countering the SCA incur a high area penalty, leaving only limited resources for random number generation. These schemes also require many random bits per execution cycle that a TRNG often cannot provide. Therefore, they resort to faster pseudo-random number generators (PRNGs) to generate random masks. Although producing statistically perfect random bits, the output of a cryptographically secure PRNG becomes entirely predictable once its inner state is leaked or guessed due to its deterministic nature. As it has recently been shown by De Meyer, to prevent side-channel leakage of a PRNG and avoid masking PRNG itself, its inner state should be refreshed with truly random bits from a TRNG much more frequently than previously required.

In the world of information security, we often see statements such as ‘secured by 128-bit AES’ or ‘protected by 2048-bit authentication’. We are used to people asking about the strength of the cryptographic algorithms deployed in a security solution. Algorithms such as the AES, RSA and ECC have a proven track record of being difficult to break. They are successfully deployed in protocols that protect our identity and the integrity and confidentiality of our data, on a daily basis. Consider, for instance, the use of SSL or TLS when you buy a book at Amazon, or when you connect to your bank account to transfer a sum of money. What we see very rarely, unfortunately, are statements about the strength of the random number generator used by a security system. System designers are typically more concerned with the power consumption and bit generation speed, than with the actual randomness of the bits generated.

This is strange, considering that in most, if not all, cryptographic systems, the quality of the random numbers used directly determines the security strength of the system. In other words, the quality of the random number generator directly influences how difficult it is to attack the system.

Take, for example, the effective strength of 3DES. Although it uses 3 keys of 56 bits each, 3DES is currently only expected to provide 112 bits of ‘effective’ security, since the best attack against it today has a complexity of 2112 bits. This still assumes that all 168 bits of the key used, are unknown and unpredictable by the attacker. So what happens if we start with key material that is partly predictable to the attacker? Immediately, the security of the system is weakened, regardless of the algorithm or protocol used. If your 128-bit key contains 16 predictable bits, using it in AES-128 doesn’t give you 128-bit protection; it only gives you 112 bits of protection, making the security of your system ‘only’ as strong as 3DES today. And it doesn’t stop with cryptographic key material. Many security protocols require random bits to remain secure, even though the protocol definition will not always call it random; typically, a protocol description will use the term ‘unpredictable’ to indicate that a certain value should be difficult to guess by an attacker. True random numbers may be required if your application uses one of the following:

1. keys and initialization values (IVs) for encryption
2. keys for keyed MAC algorithms
3. private keys for digital signature algorithms
4. values to be used in entity authentication mechanisms
5. values to be used in key establishment protocols
6. PIN and password generation
7. Nonces

A. Random Number Generation

Creating Random Numbers is hard. Especially if all you have available to do it, is digital hardware and deterministic software. Where is the randomness in that? Both are designed to behave predictably, each time, every time. Therefore, hardware and software designers, trying to find unpredictability, have to look outside of their normal operating environment to find it. Software typically uses external events (hard disk seek timing, keyboard/mouse clicks, Ethernet packet arrival intervals). Digital hardware designers have to ‘fall back’ to the analog world from which their digital environment normally tries to shield them. This typically means somehow translating the noise from a diode p-n junction, a resistor, or some other semiconductor component, into ‘unpredictable’ bit values.

B. Ring Oscillator

A ring oscillator is a device composed of an odd number of NOT gates whose output oscillates between two voltage levels, representing true and false.

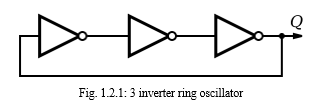
The NOT gates, or inverters, are attached in a chain; the output of the last inverter is fed back into the first. Because a single inverter computes the logical NOT of its input, it can be shown that the last output of a chain of an odd number of inverters is the logical NOT of the first input. This final output is asserted a finite amount of time after the first input is asserted; the feedback of this last output to the input causes oscillation. A real ring oscillator only requires power to operate; above a certain threshold voltage, oscillations begin spontaneously. To increase the frequency of oscillation, two methods may be used. Firstly, the applied voltage may be increased; this increases both the frequency of the oscillation and the power consumed, which is dissipated as heat.

The frequency of the simple ring oscillator is determined from the delay of each stage. A time domain graph of the three node voltages from Figure 1.2.1.

II. EXISTING SYSTEM

This paper presents a design Random number generators are indispensable components of any modern security system. With physically unclonable functions (PUFs), true random number generators (TRNGs) are the only cryptographic primitives producing truly unpredictable bits for generating secrets in symmetricand public-key cryptography. Random number generators are also extensively used in various randomization-based countermeasures for protecting cryptographic implementations against side-channel attacks (SCA). Among others, the low-latency masking schemes for countering the SCA incur a high area penalty, leaving only limited resources for random number generation . These schemes also require many random bits per execution cycle that a TRNG often cannot provide. Therefore, they resort to faster pseudo-random number generators (PRNGs) to generate random masks . Although producing statistically perfect random bits, the output of a cryptographically secure PRNG becomes entirely predictable once its inner state is leaked or guessed due to its deterministic nature. To prevent side-channel leakage of a PRNG and avoid masking PRNG itself, its inner state should be refreshed with truly random bits from a TRNG much more frequently than previously required. In addition to passing the statistical tests, modern TRNG designs should have an estimation of the amount of entropy they can provide. The entropy source is a component with nondeterministic behavior that exploits an inherently random physical process. The digitization module converts the output of the entropy source, which is often in analog form, into raw random numbers (bits). The entropy source and the digitization module together constitute a digital noise source.

Sri Durga .R et al., proposed an RNG model to increase the unpredictability of Linear Feedback Shift Registers (LFSRs) in cryptography applications. The model includes a polynomial modulator, which includes a multiplexer, counter, and comparator to select primitive polynomials. The randomness of the proposed RNG models is verified using the NIST 800-22 Test suite, and the sequences generated are random. The proposed LSFR-based RNG makes it difficult to predict sequences, providing an advantage for cryptography. The model is implemented in an FPGA device and shows that as the bit length increases, power consumption and component utilization also increase.

 Xinyu Wang et al., designed true random number generators (TRNGs) based on field-programmable gate arrays (FPGAs), which gained attention due to the need for reliable encryption. TRNGs based on ring oscillators and phase-locked loops have advantages like low resource overhead and high throughput, but they also face issues like instability and poor portability. To improve randomness, portability, and throughput, a TRNG is designed using self-timed rings (STRS) oscillations and a jitter-latch structure. The structure's portability is verified using electronic design automation (EDA) tools. The TRNG is tested on Xilinx Spartan-6 and Virtex-6 FPGAs with an automatic routing mode, showing excellent performance in randomness, robustness, and portability. The total logic power obtained from ISE power analysis results is 1.15 mW. The TRNG has stable randomness and high throughput, with optimization ability for offset caused by process deviation.

Adriaan Peetermans et al. introduces a dynamic calibration mechanism for the Coherent Sampling Ring Oscillator based TRNG (COSO-TRNG), allowing easy integration of the entropy source into complex systems. The mechanism ensures correct TRNG operation even when automatic placement is carried out or when the design is ported to another FPGA family. The COSO-TRNG generates random bits with a throughput of 3.30 Mbit/s and 1.47 Mbit/s on a Spartan 6 and a Microsemi SmartFusion2 FPGA respectively, passing AIS-31 statistical tests. However, the design has a modest area requirement and increased latency when searching for an optimal configuration.

Parangat Mittal et al., compares three modern LFSR-based Test Pattern Generators for VLSI Design and clyptography applications. The study reveals that designs with the least hardware throughput generate less random test sequences, while low power designs dissipate the least power but cannot generate a truly random sequence. The paper emphasizes the importance of designing efficient test pattern generators that utilize minimal hardware and generate the most random sequence.

III. PROPOSED SYSTEM

The entropy source of the proposed TRNG is a three-edge mode ring oscillator which consists of three inverting and three non-inverting stages, as depicted in the upper part of Fig. Three edges are simultaneously injected by each inverting NAND stage with enable signal Run. These edges will have an identical mean period since they propagate through the same stages. The propagation through identical stages significantly reduces the influence of the global and possibly adversarial noise sources, while the local Gaussian noise accumulates independently by each edge. The frequency of the resulting ring oscillator signal at the output of any of the six stages will be three times higher than the frequency of a single-edge ring oscillator with the same stages. Due to noise influence, the three edges will inevitably collide, eventually compelling the ring oscillator to a single-edge mode.

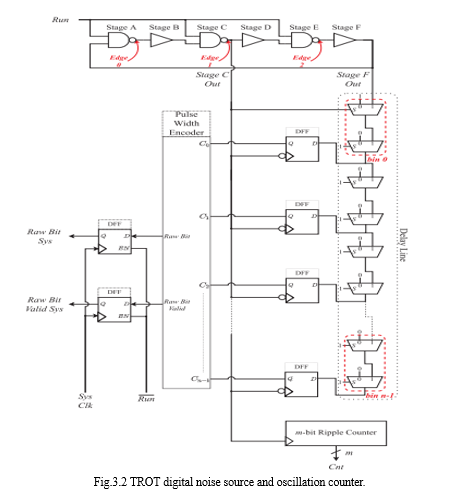
In this method, we use a technique based on a single time to-digital converter (TDC) line as a digitization element to more efficiently exploit the independent timing jitter in each edge. The use of TDC enables higher throughput since the randomness extraction from the three jittery edges can happen much earlier than waiting for the edge collapse. The TDC consists of a delay line formed by high-speed multiplexers and n falling-edge D flip-flops (DFFs) whose D inputs are connected to the outputs of the multiplexers – bins. As seen in Fig. 3, the signal from the third non-inverting stage F is connected to input 1 of the first multiplexer in the delay line. All multiplexers in the delay line have a select signal set to constant 1, except the first, whose select signal comes from the second inverting stage C. The signal from stage C is also used as a clock signal for the DFFs. This oscillator configuration thus falls into a category of multimode multi-phase oscillators.

The pulse width encoder is a combinatorial circuit that outputs a raw bit value and a valid signal based on the DFFs’ values C0 to Cn−1. The raw bit depends on the parity of the number of zeros values relative to the total number of DFFs

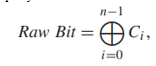
where n is always even. The raw bit valid signal is set when the first and the last DFF in the TDC have value one, and there is at least one DFF with value zero.

The unavoidable variations of the bins’ propagation delays along the delay line will influence the amount of obtainable entropy. While sampling the delay line, the setup or hold time of some DFFs in the TDC might be violated. This event leads to bubbles in the captured TDC code that can be dealt with by bin reordering, To improve the uniformity and minimize bubble manifestations in the TDC, we sacrifice the sampling precision by combining the two adjacent physical bins into one bin of the delay line. To estimate the jitter accumulated by the three edges and their oscillation period in the design phase, we use an m-bit rising edge ripple counter connected to the output of stage C. This counter can also serve as a total failure test to monitor the number of oscillations during the accumulation time tacc. If the edges collide before the raw random bit is generated due to environmental influences or an attack, the counter will have much lower values than during the regular operation. This observation can be used to raise the alarm to the user application.

A. Entropy Estimation of the Internal Random Numbers

Thus, to increase the min-entropy while maintaining high throughput and low implementation cost, we opt to use post-processing based on the binary linear codes. This post-processing represents a generalization of the commonly used XOR post-processing – parity filter. To explain it, we start with a theorem that gives the relation between the min-entropy of the random bits post-processed by any vectorial Boolean function and maximal one-dimensional bias of its output.

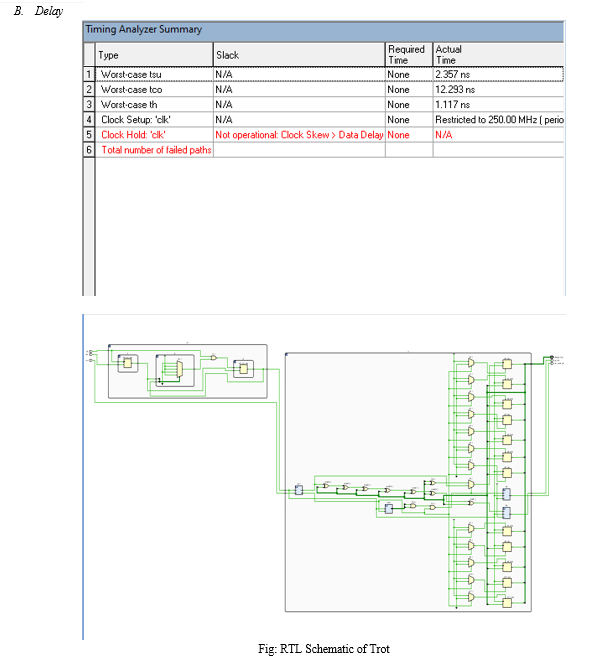
Conclusion

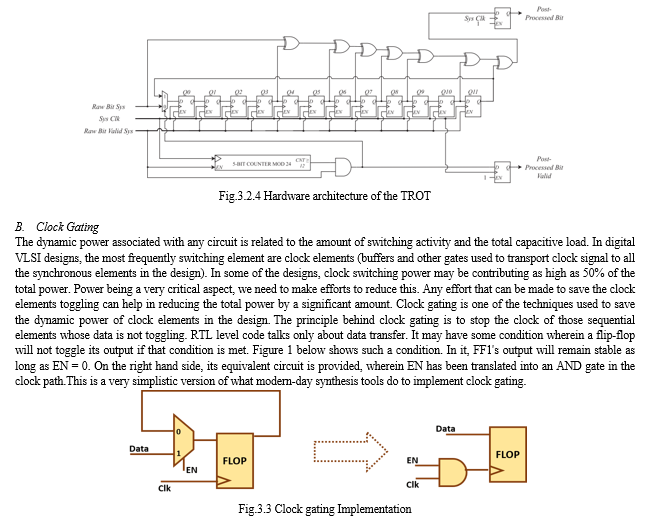
In conclusion, the TROT incorporates a three-edge mode ring oscillator with a novel TDC-based digitization technique and optimized information-theoretically secure post-processing to obtain a relatively compact design with high throughput and low design effort. These properties make our TRNG more suitable than previously reported designs to implement with the area- and randomness-consuming cryptographic systems and SCA countermeasures. Also, by using gating technique we observed a decrease in delay of overall circuit.

References

[1] L. De Meyer, “Cryptography in the presence of physical attacks: Design, implementation and analysis,” Ph.D. dissertation, Dept. Eng. Sci., Dept. Elect. Eng., KU Leuven, Leuven, Belgium, 2020. [2] L. De Meyer, “Recovering the CTR DRBG state in 256 traces,” IACR Trans. Cryptogr. Hardw. Embedded Syst., vol. 2020, no. 1, pp. 37–65, Nov. 2019. [3] M. S. Turan, E. Barker, J. Kelsey, K. McKay, M. Baish, and M. Boyle, “NIST special publication 800-90B: Recommendation for the entropy sources used for random bit generation,” NIST, Gaithersburg, MD, USA, Tech. Rep. NIST Special Publication 800-90B, Jan. 2018. [4] W. Killmann and W. Schindler, “A proposal for: Functionality classes for random number generators,” BSI, Bonn, Germany, Tech. Rep., Sep. 2011. [5] D. Li et al., “GB/T 32915-2016 information security technology— Randomness test methods for binary sequence,” Standard, Standardization Admin. PRC, Beijing, China, Tech. Rep. GM/T 0005-2012, Aug. 2016. [6] O. Petura, U. Mureddu, N. Bochard, V. Fischer, and L. Bossuet, “A survey of AIS-20/31 compliant TRNG cores suitable for FPGA devices,” in Proc. 26th Int. Conf. Field Program. Log. Appl. (FPL), Aug. 2016, pp. 1–10. [7] V. Roži´c, B. Yang, W. Dehaene, and I. Verbauwhede, “Highly efficient entropy extraction for true random number generators on FPGAs,” in Proc. 52nd Annu. Des. Autom. Conf., Jun. 2015, pp. 1–6. [8] B. Yang, V. Roži´c, M. Gruji´c, N. Mentens, and I. Verbauwhede, “ESTRNG: A high-throughput, low-area true random number generator based on edge sampling,” IACR Trans. Cryptogr. Hardw. Embedded Syst., vol. 2018, no. 3, pp. 267–292, 2018. [9] M. Baudet, D. Lubicz, J. Micolod, and A. Tassiaux, “On the security of oscillator-based random number generators,” J. Cryptol., vol. 24, no. 2, pp. 398–425, 2011. [10] B. Sunar, W. J. Martin, and D. R. Stinson, “A provably secure true random number generator with built-in tolerance to active attacks,” IEEE Trans. Comput., vol. 56, no. 1, pp. 109–119, Jan. 2007. [11] P. Kohlbrenner and K. Gaj, “An embedded true random number generator for FPGAs,” in Proc. ACM/SIGDA 12th Int. Symp. Field Program. Gate Arrays (FPGA), Feb. 2004, pp. 71–78. [12] V. Fischer and M. Drutarovský, “True random number generator embedded in reconfigurable hardware,” in Proc. 4th Int. Workshop Cryptogr. Hardw. Embedded Syst. (CHES), Aug. 2002, pp. 415–430. [13] M. Varchola and M. Drutarovský, “New high entropy element for FPGA based true random number generators,” in Proc. 12th Int. Workshop Cryptograph. Hardw. Embedded Syst. (CHES), Aug. 2010, pp. 351–365. [14] A. Cherkaoui, V. Fischer, L. Fesquet, and A. Aubert, “A very high speed true random number generator with entropy assessment,” in Proc. 15th Int. Workshop Cryptogr. Hardw. Embedded Syst. (CHES), Aug. 2013, pp. 179–196. [15] P. Lacharme, “Post-processing functions for a biased physical random number generator,” in Proc. Int. Workshop Fast Softw. Encryption, Feb. 2008, pp. 334–342. [16] L. E. Bassham et al., “A statistical test suite for random and pseudorandom number generators for cryptographic applications,” NIST, Gaithersburg, MD, USA, Tech. Rep. Special Publication 800-22, Rev. 1a, Apr. 2010. [17] K. Yang, D. Fick, M. B. Henry, Y. Lee, D. Blaauw, and D. Sylvester, “16.3 A 23Mb/s 23pJ/b fully synthesized true-random-number generator in 28 nm and 65 nm CMOS,” in IEEE Int. Solid-State Circuits Conf. (ISSCC) Dig. Tech. Papers, Feb. 2014, pp. 280–281. [18] H. Zhuang et al., “A second-order noise-shaping SAR ADC with passive integrator and tri-level voting,” IEEE J. Solid-State Circuits, vol. 54, no. 6, pp. 1636–1647, Jun. 2019. [19] H. Zhuang, J. Liu, H. Tang, X. Peng, and N. Sun, “A fully dynamic low-power wideband time-interleaved noise-shaping SAR ADC,” IEEE J. Solid-State Circuits, vol. 56, no. 9, pp. 2680–2690, Sep. 2021. [20] M. Gruji´c, V. Roži´c, B. Yang, and I. Verbauwhede, “A closer look at the delay-chain based TRNG,” in Proc. IEEE Int. Symp. Circuits Syst. (ISCAS), May 2018, pp. 1–5.

Copyright

Copyright © 2024 C. Prasannanjali, G. Sahithya, C. Aravind, C. Uday Kiran Reddy, S. Gowtham, G. Padma Priya. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.