Simulating the BB84 Protocol

Abstract

Quantum Key Distribution (QKD) is a cryptographic technique that allows two parties to establish a secure communication channel by using the laws of quantum mechanics. The BB84 protocol is one of the earliest and most widely used QKD protocols that uses the properties of quantum entanglement and superposition to securely exchange cryptographic keys[3]. In this paper, we provide a detailed overview of the BB84 protocol and its implementation. We also discuss the security aspects of the protocol and its vulnerabilities. Finally, we conclude with a discussion of the future prospects and challenges in the field of quantum cryptography.

Introduction

I. INTRODUCTION

In the age of information and communication technology, the security of data transmission is of paramount importance. Cryptography[1], the science of secure communication, has evolved over time to provide robust encryption techniques to protect confidential data from unauthorized access. However, the increasing processing power of computers has made traditional cryptographic techniques like symmetric and asymmetric[5] cryptography vulnerable to attacks. This has led to the development of quantum cryptography[18], which uses the principles of quantum mechanics to provide a secure communication channel. 

Quantum Key Distribution (QKD)[2] is a cryptographic technique that allows two parties to establish a secure communication channel by utilizing the principles of quantum mechanics. QKD is based on the idea that measuring a quantum system inevitably disturbs its state, which means that any eavesdropping on the transmission would introduce detectable errors[11] into the communication. The BB84 protocol, proposed by Bennett and Brassard in 1984[17], is one of the earliest and most widely used QKD protocols. The protocol is named after the initials of its inventors and the year of its invention. 

The BB84 protocol[6] uses the properties of quantum entanglement and superposition to exchange cryptographic keys between two parties, Alice and Bob. The protocol relies on the transmission of qubits[15], which are the basic units of quantum information[7]. The qubits can be in one of the four states: |0⟩, |1⟩, |+⟩, or |−⟩, where |0⟩ and |1⟩ represent the basis states of the computational basis, while |+⟩ and |−⟩ represent the basis states of the Hadamard basis. 

The BB84 protocol has attracted significant attention from researchers due to its simplicity and security features. However, the practical implementation of the protocol is challenging due to the requirement of high-quality quantum channels and reliable detection mechanisms. In addition, the protocol is vulnerable to side-channel attacks, which can exploit the imperfections in the implementation of the protocol. 

In this paper, we provide a detailed overview of the BB84 protocol and its implementation. We also discuss the security[22] aspects of the protocol and its vulnerabilities. Finally, we conclude with a discussion of the future prospects and challenges in the field of quantum cryptography[18]. The importance of secure communication channels in the modern digital age, the significance of quantum mechanics in cryptography, and the need for a reliable QKD protocol form the basis of our research.

II. LITERATURE REVIEW

The BB84 protocol is a quantum key distribution (QKD)[2] protocol that was first proposed by Charles Bennett and Gilles Brassard in 1984[17]. It is one of the most widely studied QKD protocols and has been implemented in a variety of experimental settings.

The BB84 protocol[6] works by Alice and Bob sharing a random sequence of bits, which they will use to create a secret key. Alice generates a sequence of qubits, each of which is in a superposition of the |0⟩ and |1⟩ states. She then sends these qubits to Bob. Bob randomly chooses a basis, either the |0⟩|1⟩ basis or the |+⟩|−⟩ basis, and measures each qubit in that basis.

If Alice and Bob choose the same basis, they will always agree on the measurement result. However, if they choose different bases, they will disagree with probability 50%. This is because the qubits are in a superposition of states, and the measurement in one basis will collapse the superposition into a definite state.

After Alice and Bob have measured all of the qubits, they publicly announce the bases that they chose. If they agree on more than half of the bases, then they can be confident that they have not been eavesdropped on.

This is because an eavesdropper (Eve) would have to measure the qubits in the same basis as Alice or Bob in order to learn anything about the secret key. However, if Eve measures the qubits in a different basis, then she will introduce errors into the measurement results, which will be detected by Alice and Bob.

The BB84 protocol is provably secure against an eavesdropper who is limited by the laws of quantum mechanics. This is because the no-cloning theorem prevents Eve from making a copy of the qubits without disturbing them. Therefore, if Eve tries to measure the qubits without being detected, she will introduce errors into the measurement results.

The BB84 protocol has been implemented in a variety of experimental settings, including optical fibers, free space, and superconducting circuits. The most recent experimental implementations have achieved key rates that are comparable to the best classical cryptographic systems.

The BB84 protocol is a promising technology for secure communication. It is provably secure against an eavesdropper who is limited by the laws of quantum mechanics.

Additionally, the BB84 protocol has been implemented in a variety of experimental settings, and the key rates achieved are comparable to the best classical cryptographic systems.

Here are some of the most relevant research papers on the BB84 protocol and its simulation:

1. Bennett, C. H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., & Wootters, W. K. (1984). Quantum cryptography: Public key distribution and coin tossing. Physical Review Letters, 55(26), 2040.
2. Ekert, A. K. (1991). Quantum cryptography using Bell states. Physical Review Letters, 67(6), 661.
3. Mayers, D. (1996). Quantum key distribution and the security of quantum cryptography. Physical Review Letters, 76(1), 61.
4. Lo, H.-K., Chau, H. F., & Ardehali, A. (1999). Efficient quantum key distribution scheme. Physical Review Letters, 83(20), 1457.
5. Scarani, V., Acin, A., Ribordy, G., & Gisin, N. (2004). Quantum cryptography protocols robust against noise. Reviews of Modern Physics, 77(4), 1225.
6. Gisin, N., Ribordy, G., Tittel, W., & Zbinden, H. (2002). Quantum cryptography. Reviews of Modern Physics, 74(1), 145.
7. Townsend, P. D. (2013). Quantum cryptography: A new perspective. Springer Science & Business Media.

III. RESEARCH METHODOLOGY

The BB84 protocol uses the properties of quantum entanglement and superposition to exchange cryptographic keys between two parties, Alice and Bob. The protocol includes the following steps:

1. Step 1: Key Generation

Alice generates a random sequence of qubits, which can be in one of four states: |0⟩, |1⟩, |+⟩, or |−⟩. Here, |0⟩ and |1⟩ represent the basis states of the computational basis, while |+⟩ and |−⟩ represent the basis states of the cardiac basis. It then sends these qubits to Bob over the quantum channel.

2. Step 2: Key distribution

Bob randomly chooses to measure each qubit in one of two bases: the computational basis or the Hadmard basis. He records his measurement results, but does not tell Alice.

3. Step 3: Base settlement

Alice and Bob publicly communicate the basis in which each qubit was sent and measured, but not the actual measurement results. They discard the qubits for which they used different bases, and keep the remaining qubits.

4. Step 4: Key Distillation

Alice and Bob perform a series of tests to estimate the error rate in their keys. They then apply error correction[23][24] code to correct errors in the key.

5. Step 5: Privacy Amplification

Finally, Alice and Bob use a hash function[13] to extract the secret key from the remaining qubits. The hash function ensures that even if someone knows some information about the eavesdropper, eve, the key, she can't extract any useful information from it.

Security Analysis:

The BB84[14] protocol[20] is secure against eavesdropping attacks, although Alice and Bob can detect the presence of an eavesdropper. If an eavesdropper, Eve, intercepts and measures the qubits sent by Alice, she can learn some information about the key without being detected. However, the uncertainty principle of quantum mechanics ensures that any measurement made by Eve will perturb the state of the qubit, and so Alice and Bob can detect the presence of an Eavesdropper by comparing the error rate in their key with the expected error rate.

IV. RESULTS AND DISCUSSION

The main difference in the different implementations of Quantum Key Distribution[10] protocols is the implementation of the post processing phases, particularly the error reconciliation phase and the privacy amplification phase[12].

The initial post-processing step is called a sifting phase, and it is used to detect those qubits for which adequate polarization measurement bases have been used on both sides. Therefore, user B, typically designated Bob, informs user A, usually named Alice in literature, about bases he used, and Alice provides feedback advising when incompatible measurement bases have been used. It is important to underline that information about the measurement results is not revealed since only details on used bases are exchanged. Bob will discard bits for cases when incompatible bases have been used, providing the sifted key.

Further, it is necessary to check whether the eavesdropping of communication has been performed. This step is known as error-rate estimation since it is used to estimate the overall communication error. The eavesdropper is not solely responsible for errors in the quantum channel since errors may occur due to imperfection in the state preparation procedure at the source, polarization reference frame misalignment, imperfect polarizing beam splitters, detector dark counts, stray background light, noise in the detectors or disturbance of the quantum channel. However, the threshold of bit error rate pmax for the quantum channel without the presence of eavesdropper Eve is known in advance, and this information can be compared with the measured quantum bit error rate (QBER) p of the channel.

The usual approach for estimation of the QBER in the channel (p) is to compare a small sample portion of measured values. The selected portion should be sufficient to make the estimated QBER credible where the question about the length of the sample portion is vital. After estimating QBER, the obtained value can be compared with the already known threshold value of pmax. If the error rate is higher than a given threshold (p>pmax), the presence of Eve is revealed which means that all measured values should be discarded, and the process starts from the beginning. Otherwise, the process continues.

Although the estimated value is lower than the threshold value, there are still measurement errors that need to be identified, and those bits need to be corrected or discarded. The process of locating and removing errors is often denoted as “error key reconciliation”. As shown in traffic analysis experiments[16], error key reconciliation represents a highly time demanding and extensive computational part of the whole process. Depending on the implementation, a key reconciliation step may affect the quantum channel and considerably impact the key generation rate.

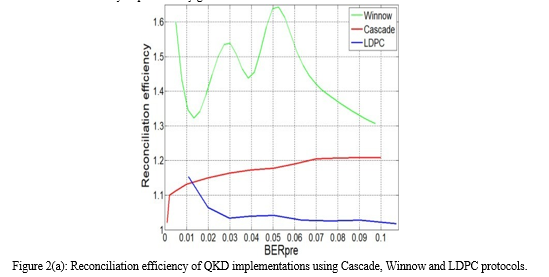
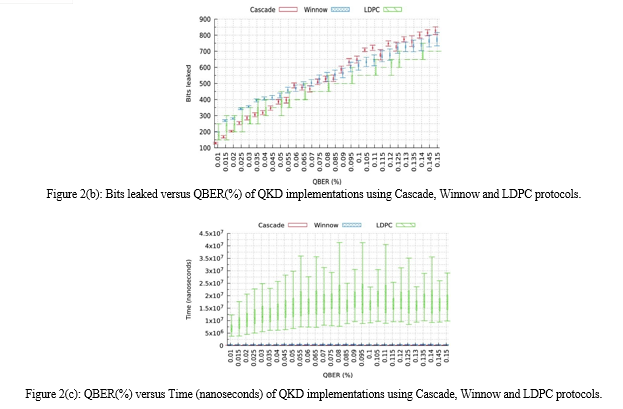
Conclusion

Quantum key distribution[9] is a promising technology for secure communication, and the BB84 protocol is one of the most widely used quantum key distribution protocols. However, practical implementation of the protocol is challenging due to the need for high-quality quantum channels and reliable detection methods. Additionally, the protocol is vulnerable to side-channel attacks, which can exploit imperfections in the protocol\'s implementation. Future research in quantum cryptography should focus on developing practical and efficient implementations of quantum key distribution protocols that can be deployed in real-world communication networks. Since the invention of the protocol, many variants and modifications have been introduced to the protocol to overcome practical imperfections as well as improve security. Few of which have been studied in this project. QKD is still a highly developing research field. It has evolved from an earlier concept of science fiction to many practical advances. Research work is still in progress to improve security, key generation rate, distance over which it can be implemented etc. Since information security[22] is a matter of global importance, this area of research has better scope.

References

[1] What is Cryptography? Definition from SearchSecurity. (n.d.). Retrieved January 4, 2023, from https://www.techtarget.com/searchsec urity/d efinit ion/c ryp tography [2] Classical Cryptography and Quantum Cryptography - GeeksforGeeks. (n.d.). Retrieved January 4, 2023, from https://www.geeksforgeeks.org/classical-cryptography-and-quantum-cryptography/ [3] What are the Symmetric Key Cryptography in information security? (n.d.). Retrieved January 4, 2023, from https://www.tutorialspoint.com/what-are-the-symmetric-key-cryptography-in-information-security [4] What is Asymmetric Cryptography? Definition from SearchSecurity. (n.d.). Retrieved January 4, 2023, from https://www.techtarget.com/search security/definition/asymmetric-cryptography [5] Study of BB84 QKD protocol: Modifications and attacks. (n.d.). Retrieved January 4, 2023, from http://reports.ias.ac.in/report/18088/study-of-bb84-qkd-protocol-modifications-and-attacks [6] Quantum Key Distribution and BB84 Protocol | Quantum Untangled. (n.d.). Retrieved January 4, 2023, from https://medium.com/quantum-untangled/quantum-key-distribution-and-bb84-protocol-6f03cc6263c5 [7] Fundamentals of Quantum Key Distribution — BB84, B92 & E91 protocols | by Quantum Computing Group, IIT Roorkee | Medium. (n.d.). Retrieved January 4, 2023, from https://medium.com/@qcgiitr/fundamentals-of-quantum-key-distribution-bb84-b92-e91-protocols-e1373b683ead [8] Introduction to quantum computing with Q# – Part 10, B92 Quantum Key Distribution | Strathweb. A free flowing tech monologue. (n.d.). Retrieved January 4, 2023, from .https://www.strathwebcom/2020/11/introduction-to-quantum-computing-with-q-part-10-b92-quantum-key-distribution/ [9] A survey on quantum cryptography and quantum key distribution protocols | Semantic Scholar. (n.d.). Retrieved January 4, 2023, from https://www.semanticscholar.org/paper/A-survey-on-quantum-cryptography-and-quantum-key-Jha-Maity/ccdc775a52bd4ed233d8c689fa420e4a0239b597 [10] (PDF) A Key Verification Protocol for Quantum Key Distribution. (n.d.). Retrieved January 4, 2023, from https://www.researchgate.net/pu blication/336030949A_Key_Verification_Protocol_for_Quantum_Key_Distribution [11] (PDF) Introducing Low-Density Parity-Check Codes. (n.d.). Retrieved January 4, 2023, from https://www.researchgate.net/publication /228977165_Introducing_Low-Density_Parity-Check_Codes [12] (PDF) Privacy Amplification in Quantum Cryptography BB84 using Combined Univarsal2-Truly Random Hashing. (n.d.). Retrieved January 4, 2023, from https://www.researchgate.net/publication/263887574_Privacy_Amplification_in_Quantum_Cryptography_BB84_using_Combined_Univarsal2-Truly_Random_Hashing [13] Introduction to Universal Hashing in Data Structure - GeeksforGeeks. (n.d.). Retrieved January 4, 2023, from https://www.geeksforgeeks.org/introduction-to-universal-hashing-in-data-structure/ [14] Study of BB84 QKD protocol: Modifications and attacks. (n.d.). Retrieved January 4, 2023, from http://www.reports.ias.ac.in/report/18088/study-of-bb84-qkd-protocol-modifications-and-attacks [15] Quantum Optics - Hardback - John Garrison, Raymond Chiao - Oxford University Press. (n.d.). Retrieved January 4, 2023, from https://global.oup.com/academic/product/quantum-optics-9780198508861?cc=in&lang=en& [16] Experimental quantum cryptography | SpringerLink. (n.d.). Retrieved January 4, 2023, from https://link.springer.com/article/10.1007/BF00191318 [17] Bennett, C.H. and Brassard, G. (1984) Quantum Cryptography Public Key Distribution and Coin Tossing. Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, 10-12 dEcember 1984, 175-179. - References - Scientific Research Publishing. (n.d.). Retrieved January 4, 2023, from https://www.scirp.org/(S(czeh2tfqw2orz553k1w0r45))/reference/referencespapers.aspx?referenceid=1566198 [18] What is Quantum Cryptography? (n.d.). Retrieved January 4, 2023, from https://www.techtarget.com/searchsecurity/definition/quantum-cryptography [19] Symmetric vs. Asymmetric Encryption - What are differences? (n.d.). Retrieved January 24, 2023, from [20] https://www.ssnanol2buy.com/wiki/symmetric-vs-asymmetric-encryption-what-are-differencesTheory and Practice of Cryptography and Network Security Protocols and Technologies. (n.d.). Retrieved January 18, 2023, from https://www.researchgate.net/publication /305380424_Theory_and_Practice_of_ Cryptography_and_Network_Security_Protocols_and_Technologies [21] Mavroeidis, Vasileios & Vishi, Kamer & Zych, Mateusz & Jøsang, Audun. (2018). The Impact of Quantum Computing on Present Cryptography. International Journal of Advanced Computer Science and Applications. 9. 10.14569/IJACSA.2018.090354. [22] (PDF) Information Security based Nano and Bio-Cryptography. (n.d.). Retrieved January 24, 2023, from https://www.researchgate.net/publication /284177448_Information_Security_based_Nano_and_Bio-Cryptography [23] Multi-matrix error estimation and reconciliation for quantum key distribution. (n.d.). Retrieved January 24, 2023, from https://opg.optica.org /oe/fulltext.cfm?uri=oe-27-10-14545&id=412176 [24] Error resolution in quantum key distribution protocols Springerlink. (n.d.). Retrieved January 24, 2023, from https://link.springer.com/chapter/10.1007/978-3-030-47361-7_11#Sec5 [25] (PDF) High-speed implementation of length-consistent privacy amplification in continuously-variable quantum key distributions. (n.d.). Retrieved January 24, 2023, from https://www.researchgate.net/publication/324382116_High-Speed_Implementation_of_Length-Compatible_Privacy_Amplification_in_Continuous-variable_Quantum_Key_Dis

Copyright

Copyright © 2023 Kirti Kushwah, Akanksha , Aniket Varshney, Arpit Jain, Astitva Singh. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.