Designing, Solid Modeling and Stress Analysis of Horizontal Axis Wind Turbine Blade

Abstract

Wind energy is one of the clean renewable forms of energy that can handle the existing global fossil fuel crisis. Wind energy is captured by Wind turbine which converts kinetic energy of the wind into the mechanical energy and then this energy is transformed into electrical energy. The objective of this study is to design a 5kW wind turbine blade which includes selection of the blade airfoil based on CL/CD ratio, linearization of geometric parameters of the blade, solid modeling of blade profile and estimation of tangential, thrust forces and total power of the designed blade with the selection of the best material. NACA 4406 airfoil is selected based on the CL/CD ratio for various Reynolds number of flow. Geometric parameters of the blade are calculated through R programming using BEM theory by dividing the blade span into 40 sections, which are further linearized at 50% and 90% of the blade length. The lift and the drag forces acting on each of the 40 elements of the designed blades are calculated through R program and finally the power developed for the 3 bladed turbo-generator set is calculated. Results shows lift/drag forces increases along the blade span whereas the power curve shows bell curve characteristics. Finally, von mises stresses and the tip deflections are simulated in QBlade simulation tool for different blade materials, and based on the failure criteria, Epoxy carbon material is chosen for the blade. The modern wind turbine market is dominated by the horizontally mounted three blade design. A comprehensive look at blade design has shown that an efficient blade shape is defined by aerodynamic calculations based on chosen parameters and the performance of the selected airfoils . The stress analysis reveals that the blade can be modelled as a simple beam with a built in support at the hub end.

Introduction

I. INTRODUCTION

When selecting an airfoil section for a wind-power generator the average working speed is just the initial parameter in the analysis, it is also important to consider the atmospheric pressure, air density, air viscosity and the dimensions of the turbine blade. Therefore, a constant that relates these parameters is needed to characterize the air flow, is the Reynolds number, henceforth called Re, will fulfill this condition. Also, an important identifier for the efficiency of an airfoil is the Glide Ratio (GR) which relates the lift coefficient (Cl) and the drag coefficient (Cd), the greater the GR the best is the Cl per unit of Cd. So based on GR and Re a particular airfoil profile will be selected from National Advisory Committee for Aeronautics (NACA) 4-digit series, followed by determination of the chord lengths and blade twist angles which are calculated along the blade span from hub to tip, using Blade Element Momentum(BEM) theory for an optimum angle of attack for the selected airfoil profile using a computer program. BEM is a combination of both Axial Momentum Theory(AMT) and Blade Element Theory(BET). In AMT the relationship between flow parameters are derived for both axial and tangential flow. However, in BET we got information related to the blade characteristics or design aspects of the rotor. Here in our design BEM theory will be used which combines both the flow parameters with the blade profile characteristics and provides us more insight to the design parameters of the wind turbine blade. But the geometric parameters derived from BEM theory will vary in a non-uniform manner along the blade length. So such kind of blades are normally difficult to manufacture and lead to an uneconomic use of materials. In order to reduce such problems, the chords and blade angles are linearized using variable chord and variable blade angle linearization technique using a computer program. The final design parameters of the blade are used to model a 3D solid profile of the blade which is further used for failure analysis in QBlade software using Von mises stress theory. Mises stress is usually used for determining whether an isotropic and ductile material will yield when subjected to a complex loading condition which is accomplished by calculating the von Mises stress and comparing it to the material's yield stress, which constitutes the von Mises Yield Criterion.

II. LITERATURE REVIEW

Wind energy has been shown to be one of the most viable sources of renewable energy. Rotor blade is a key element in a wind turbine generator system to convert wind energy in to mechanical energy. Most blades available for commercial grade wind turbines incorporate airfoil shaped cross sections. A lot of literature works have been reviewed to have a better understanding of how to implement the design . A few of the literatures are mentioned. Muiruri P.I. and Motsamai O.S. et al. [2] have described in detail the 3D CFD simulations of a wind turbine blade and its validation using ANSYS software as a tool . Biadgo A.M. and Aynekulu G. et al. [3] have came up with an aerodynamic design of a HAWT blade with a rotor power of 1 kW using BEM theory. The design also gives the 3D view of designed blade elements. Najar F.A. and Harmain G.A. et al. [6] reviewed the design optimization of wind turbine blades through investigating the design methods and analyzing the performance of the blades which included wind turbine blade geometric design and optimization, aerodynamics analysis, wind turbine blade structural design and dynamics analysis . Liu X. , Wang L. and Tang X. et al. [8] demonstrated a novel optimal blade design method for an Fixed pitch fixed speed wind turbine through adopting linear radial profiles of the blade chord and twist angle and optimizing the slope of these two lines. The radial profiles of the blade chord and twist angle are linearized on a heuristic basis with fixed values at the blade tip and floating values at the blade root based on the preliminary blade design, and the best solution is determined using the highest Annual Energy Production for a particular wind speed Weibull distribution , as the optimization criteria with constraints of the top limit power output of the wind turbine. Sarkar A. and Behera D.K. et al. [11] has given an insight into the design aspects of a wind turbine, like turbine blade design, wind power and output power calculation. The wind turbine blades power and efficiency has been measured at different tip-speed-ratios as well as calculated using software tool. Mutkule K. , Gorad P.P. and Raut S.R. et al. [18] aimed at for validation of strength of the blade using finite element analysis in  ANSYS for different materials after solid modelling of the same was carried out using CATIA V5 . The design and static analysis of composite wind mill blade had also been carried and the comparison between different composite materials are made under same load condition .

III. METHODOLOGY

Here for the airfoil selection, NACA 4-digit series airfoils are taken from NASA database and six cambered airfoil profiles NACA 4406, NACA 4409, NACA 4412, NACA 4415, NACA 4418, NACA 4421 are selected for the analysis. The analysis will be done in QBlade software where all the above NACA 44XX airfoils will be simulated for their glide ratio against angle of attacks. The variation of glide ratio with Reynolds no will also be taken into consideration. Finally, an airfoil will be selected from the 6 numbers NACA 44XX profiles and its profile will be simulated in QBlade software. The maximum power coefficient(Cp) is assumed to be around 0.35 with the expected mechanical and electrical efficiency to be 80%. A 3 bladed commercial turbine rotor will be designed with an average velocity of wind is assumed to be 8 m/s with electrical power output of 5 kW. Blade tip speed ratio is selected as 8. After getting the angle of attack from the airfoil selection, the chord length and the blade twist angles will be calculated along the blade span using Blade Element Momentum theory with the help of R programming. Further linearization of the geometric parameters of the blade will be done with the help of R programming using variable chord and variable blade twist angle technique. Taking the selected NACA 44XX airfoil, linearized blade chord lengths and twist angles along the blade span, a solid 3D profile of the blade will be modeled using QBlade software. Further analysis of the solid blade profile will be carried out for its failure criteria using von mises stress analysis by representing the three-dimensional stress state as a single positive stress value, known as von mises stress. If this equivalent stress is greater or equal to the yield limit of the same material under simple tension, then the material will fail. The von mises stresses of different materials like carbon fiber, steel and aluminum etc. for the designed blade are simulated through QBlade software and finally compared with their respective yield strengths. Finally, the different profiles of the designed wind turbine blade are evaluated at by using R programming.

IV. AIRFOIL SELECTION

A. NACA XXXX Series Airfoil

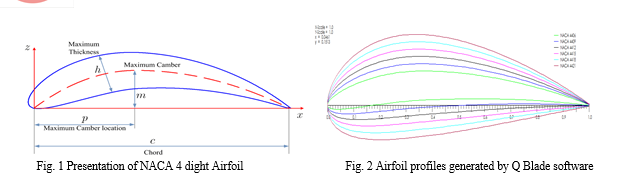
The National Advisory Committee for Aeronautics (NACA) used a four-digit numbering system to describe a large number of airfoil sections. The first family of air foils designed by NACA was the Four-Digit Series. The first digit specifies the maximum camber (m) in percentage of the chord (air foil length), the second indicates the position of the maximum camber (p) in tenths of chord, and the last two numbers provide the maximum thickness (h) of the air foil in percentage of chord. For example, the NACA 2415 air foil has a maximum thickness of 15% with a camber of 2% located 40% from the air foil leading edge (or 0.4c). Fig.1 presents the graphical profile of NACA 4-digit airfoil. NACA 4406, NACA 4409, NACA 4412, NACA4415, NACA 4418, NACA 4421 are considered for the Horizontal Axis Wind Turbine (HAWT) blade design analysis. Fig.2 present the Airfoil profiles generated using QBlade software.

B. Variation of CL/CD vs Angle of Attack for Different Reynolds Number and Different Airfoils

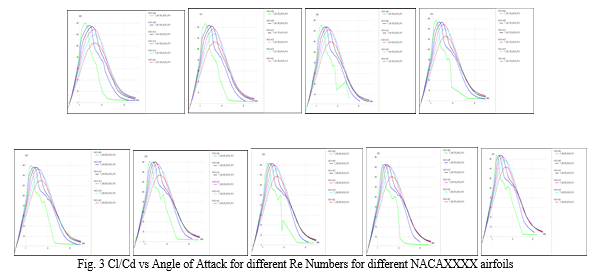
Reynolds number (Re) is the single parameter which considered all the parameters to characterises the airflow . Selection of an Airfoil on the basis of average wind speed is one of the criteria. Other important parameters to be considered are atmospheric pressure, air density, air viscosity and the dimensions of the generator. Different NACA XXXX airfoil are considered in the analysis. Also, an important identifier for the efficiency of an Airfoil is the Glide Ratio (GR), which relates the lift coefficient (Cl) and the drag coefficient (Cd). That means greater the GR, Cl per unit of Cd is maximum. For the selection of a particular Airfoil for blade design, 6 numbers of NACA 4-digit series are considered in the Qblade simulation tool. Qblade is an open-source, cross-platform simulation software for wind turbine blade design and aerodynamic simulation. Simulation of all 6 numbers airfoils are carried out for different Glide ratio against angle of attacks for different Re numbers. To set up the simulation it was necessary to create a batch analysis considering 3 constant parameters, and a variable factor for each process. The first assigned parameter was Re, then, due to the wind speeds considered for this study, the calculated value of the Mach number did not exceed 0.02. The software considers values under 0.3 as incompressible flow, so any value below this is discarded and the return value in the results is 0. Due to this reason, the Mach number is defined as 0 for every batch analysis. Finally, the "Ncrit” is the factor that amplifies the frequency in which the fluid enters in transition, this value depends on environmental perturbations in which the Airfoil will operate. For Ncrit a value of 9 is selected, which is a standard value for a normal wind tunnel experiment simulation. The angle of attack (α) is defined as the independent variable in the simulation with values between 0 and 20 degrees. In this range the maximum Cl/Cd is achieved. The simulation results of 9 batches for Cl/Cd vs angle of attack against different Reynolds number are presented in Fig. 3.

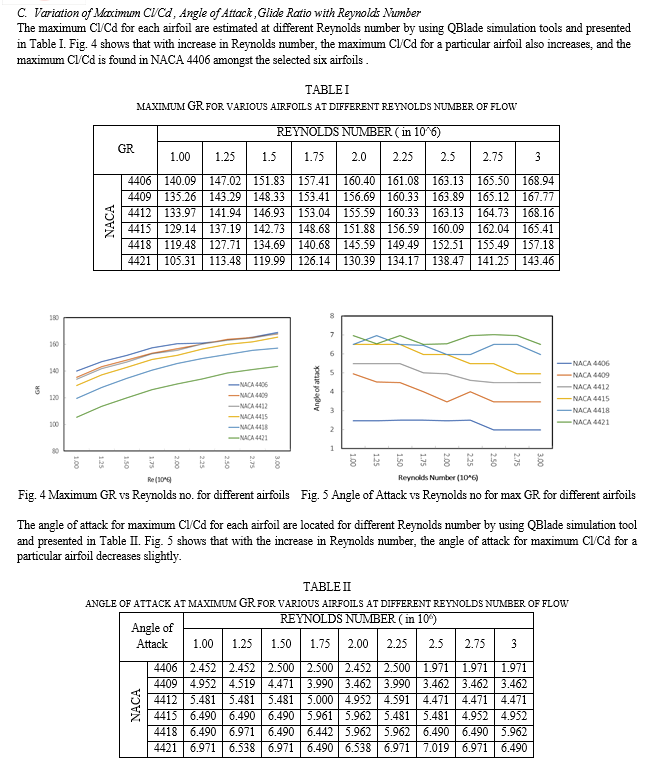
The airfoil thickness of the NACA 4406, NACA 4409, NACA 4412, NACA 4415, NACA 4418, and NACA 4421 increases in ascending order from 6%, 9%, 12%, 15%, 18% and 21% of the chord length. It is observed from Fig. 6 that for different Reynolds number, the maximum glide ratio for NACA 4406 is the highest followed by NACA 4409, NACA 4412, NACA 4415, NACA 4418, NACA 4421. In other words, with the increase in thickness of airfoil the maximum GR decreases.

D. CL/CD for Different Reynolds Number of NACA 4406 Airfoil

While selecting an airfoil for HAWT blade our main concern is to maximize the lift force and minimize the drag force, as it is the lift force which is responsible for the rotation of the blades. Hence, Cl/Cd ratio is to be maximized for different Reynolds numbers. The ratio Cl/Cd for an Airfoil is maximum at a particular angle of attack. The blade twist angle will vary along its length for a particular angle of attack. Fig. 7 presents the simulation results of NACA 4406 Airfoil for Cl/Cd vs angle of attack, for Reynolds number variation from 1.00 – 3.00 x 106. The angle of attack is selected as 2.5 degree for the design of blade.

E. Lift Coefficient at Different Angle of Attack for Various Reynolds Number of NACA 4406 Airfoil

The lift coefficient can be calculated numerically or determined from wind tunnel tests for a given angle of attack. Here the wind tunnel tests are simulated using QBlade software for 0 to 20 degrees of angle of attack and variation of Reynolds number from 1-3 x 106 in steps of 0.25 for NACA 4406 Airfoil. Fig. 8 shows that an almost linear increase in lift coefficient with the increase in angle of attack. At higher angle of attack, a maximum point is reached, after which the lift coefficient reduces. The angle at which maximum lift coefficient occurs is the stall angle of the airfoil, which is approximately 100 for NACA 4406 airfoil. The lift coefficient for NACA 4406 airfoil for Re 1-3 x 106 is 0.75 at angle of attack of 2.5 degree. This optimum value of lift coefficient is used in designing of the blade.

C. Calculation of Chord Length and Blade Setting Angle with Linearization

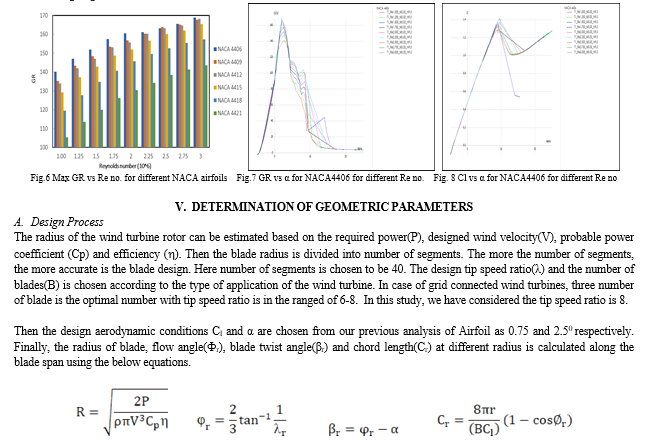
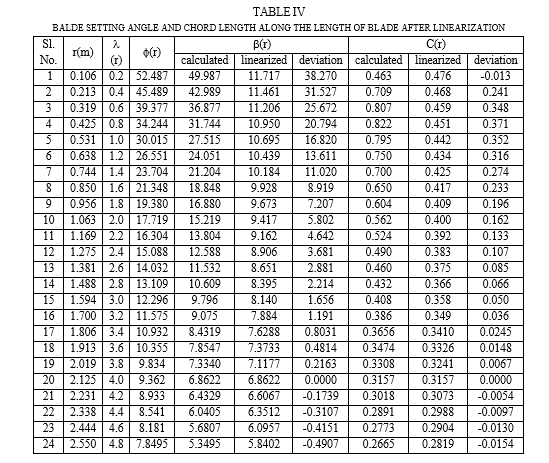
The chord length and blade twist vary in a non-uniform manner along the blade length. Such blades are normally difficult to manufacture and lead to an uneconomic use of materials. In order to reduce, these problems, it is possible to linearize the chords and blade angles. 75% of the power that is extracted by the rotor from the wind, is extracted by the outer half of the blades. This is because that the blade swept area varies with the square of the radius, and also efficiency of the blade is less at smaller radius, where the local tip speed ratio is low. On the other hand, at the tip of the blade, the efficiency is low due to the tip losses. Hence, the linearization has done in between 50-90% of the radius using variable chord and variable blade twist technique. A computer function “geometry_after_linearization” is created using R program whose final output of is directed to “after_linearization.csv” file as shown in Table IV. It is seen that the deviation of non-linearized and linearized values of chord length and blade twist angle from 50% to 90% of the blade span is negligible but the deviations are higher below 50% of the blade span.

Linearization of chord for easing the manufacturing of turbine blade has been a common practice in the industry. However, this leads to a deviation in the aerodynamic performance. So, a decrease in production cost by linearization of chord and twist angle geometry between 50% and 90% of radial length is achieved at the expense of blade performance. Blade geometries were described at 40 radial sections. A non-linear calculated chord distribution and β was arrived at , based on BEM theory. Linearization was based on a simple two-point scheme, where the linear slope of chord and β distribution variation along the span was obtained by joining the 90% chord length with the chord length at the 20th radial section & 90% β with the β at the 20th radial section. These two lengths and β were computed from BEM theory. The respective linearized graphs were superimposed in the same non linearized chord and β figure. All the calculations and the plot of graphs for the distributions were obtained using R program as shown in Fig. 10 and Fig. 11

VI. SOLID MODELING

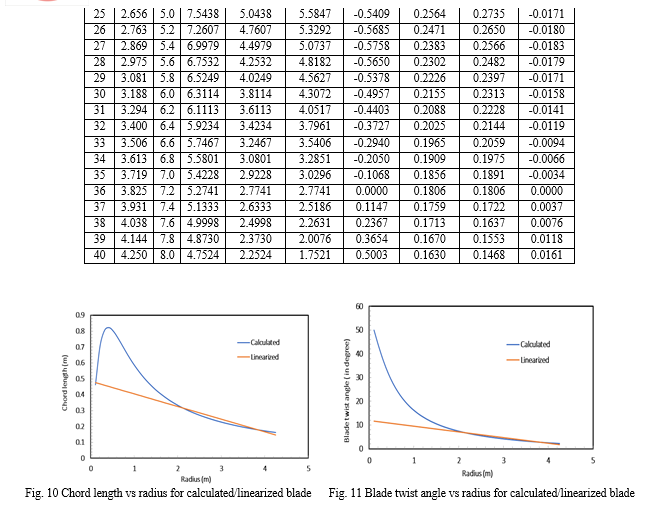
The chord lengths and blade twist angles are estimated in the different segment along the blade length for before and after linearization and are used in solid blade design sub-module of QBlade software to generate the 3D blade geometry for both before and after linearization. A blade consists of 40 numbers of positions along the blade length for the NACA 4406 Airfoil.  The number of blades of the turbine rotor is considered as 3, in QBlade software for generation of the 3D geometry. The hub radius, which is the position where the blade root is connected to the hub of the turbine is assumed to be zero as it is negligible compared to the overall length of the blade which is 4.25 m. In the solid profile design, section at 0 m radius is assumed to be a point rather than a circular foil. The radial positions of a blade are the distances of Airfoil sections from the turbine’s hub centre. The distances of the Airfoil sections from the centre for both before and after linearization are shown in Fig. 12 and Fig. 13 respectively. The blade twist angle adds a twist at every section of the blade. The 3D geometry of the blade design is used for further analysis. Fig. 14 and Fig. 15 represents the orthographic 3D view of solid blade geometry with and without filled NACA 4406 airfoils before linearization of chord length and blade twist angle. Fig. 16 presents the orthographic 3D view of solid blade geometry with coordinate axes. Fig. 17 and Fig. 18 represents the orthographic 3D view of solid blade geometry with and without filled NACA 4406 airfoils after linearization of chord length and blade twist angle. Fig. 19 presents the orthographic 3D view of solid blade geometry with coordinate axes after linearization.

VII. DETERMINATION OF AERODYNAMIC FORCES

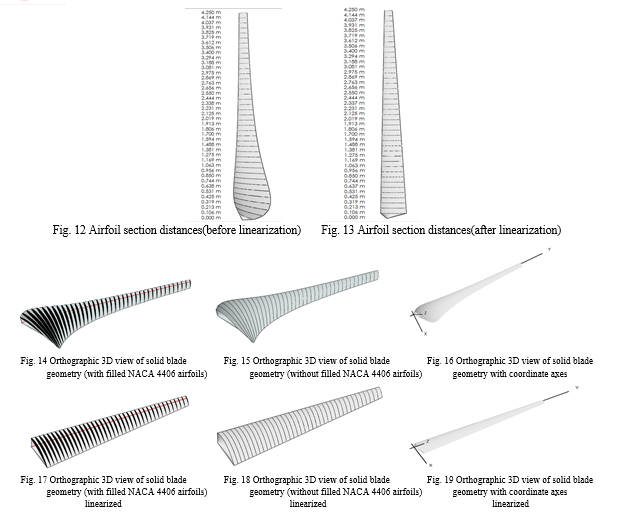
The blade angles and chord length distributions as well as the velocity triangles and force distributions of the wind turbine blade Airfoil is shown in Fig. 20 and Fig. 21 respectively. Here, the blade is divided into 40 equal sections and ‘dr’ is the length of each section. Radius of rotor axis to each section mid are denoted by rei, the subscript i refers to the section number. Firstly, the mid radius of each section from rotor axis is calculated.

Then the relative wind velocity of each section wi is calculated. In this analysis axial induction and tangential induction factors as well as blade tip losses are not taken into consideration. Then the projected elemental areas dAbi of each section in the rotor plane is calculated for all the 40 number of sections. Finally, the lift dFLi and drag dFDi forces acting on each elementary sections are calculated along the blade span by taking CL= 0.75 and CD = 0.01. The component forces of dFLi and dFDi along the rotor axis and the rotational plane are taken into account for calculation of both axial thrust force dFthrust_i and tangential dFtangential_i forces of each section.

Finally, each elemental torque dMi and elemental power dPi are calculated along the blade span for 40 sections. Total power generated by the wind turbine rotor is calculated by summation of all dPi , which gives the power absorbed by a single blade multiplied by number of blades, which is the total power absorbed by the rotor. The procedure adopted for calculation of total power generated by the wind turbine rotor is summarized in Fig. 22.

VIII. STRESS ANALYSIS

A. Blade Materials

The wind turbine blade is modelled in QBlade software and analysed for five different materials. This study explores the von mises stress analysis for different materials generated due to aerodynamic forces of a Wind Turbine Blade using QBlade software. The aim of the analysis is to compare the different materials for strength and to select the best material for the wind turbine blade. In general, ideal materials should meet the following criteria.

1. Wide availability
2. Low density and low cost
3. High strength to withstand strong loading of wind and gravitational force of the blade itself
4. High Corrosion and fatigue resistance to withstand cyclic loading
5. High stiffness
6. High fracture toughness
7. The ability to withstand environmental impacts such as lightning strikes, humidity, and temperature
8. The blades must be stiff to prevent collision with the tower under extreme loads. Local stiffness must be also sufficient to prevent extreme loads and stability of components under compression (to avoid local or global buckling)

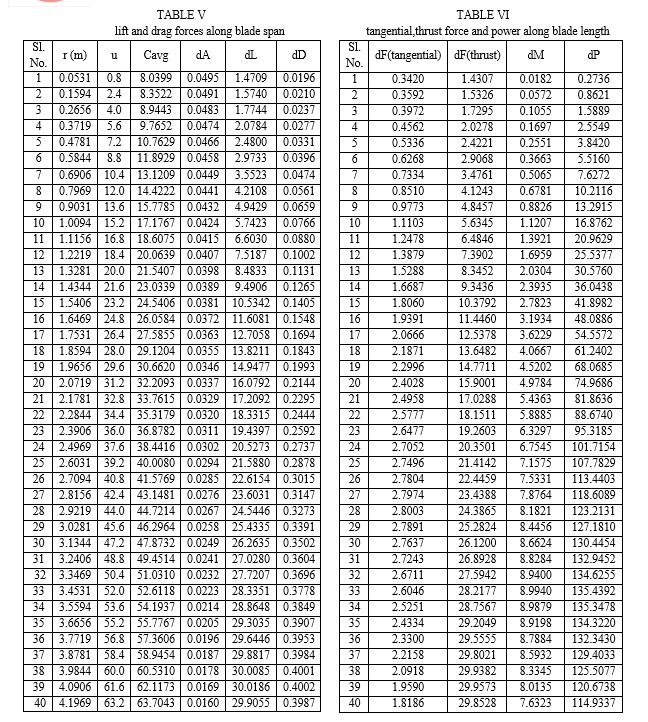
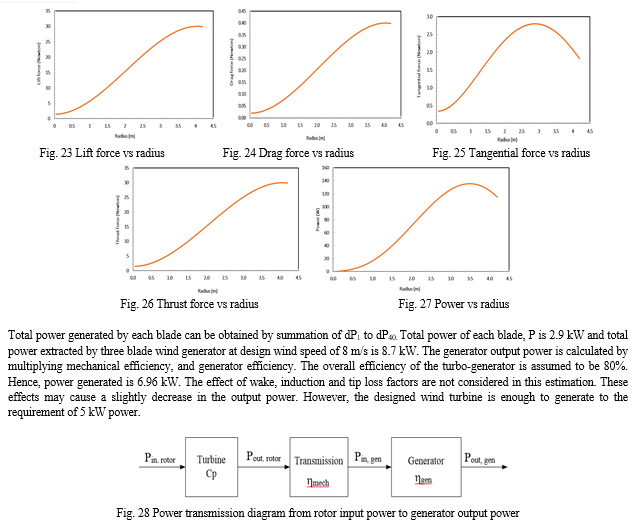
In order to ensure the required shape stability, strength and damage resistance of the wind turbine rotor blades, the blades are usually produced from long fibre reinforced polymer laminates. In these composites, long fibres ensure longitudinal stiffness and strength, while the resin matrix is responsible for fracture toughness, delamination strength and out-of-plane strength and stiffness of the composite. Usually the blade used are made of fiber-reinforced material. The material used for the present study are Structural Steel, E-glass, S-glass, Epoxy carbon, Aluminum alloy. The properties of the materials are shown in Table VI.

C. Simulation of Maximum Blade Tip Deflection

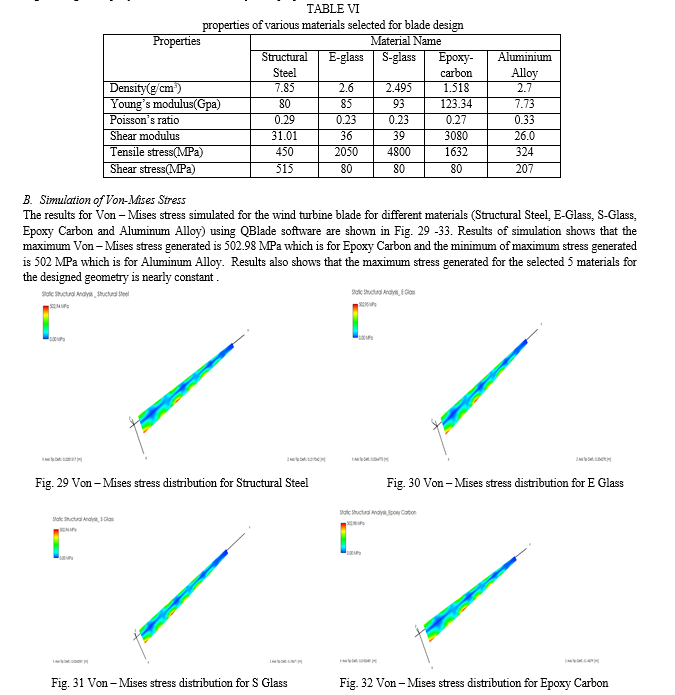
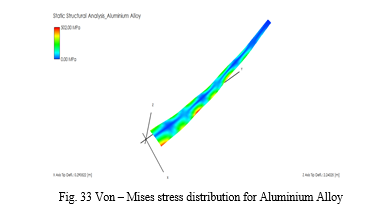
The simulated results for maximum blade tip deflection due to aerodynamic forces for the designed wind turbine blade geometry for different materials (Structural Steel, E-Glass, S-Glass, Epoxy Carbon and Aluminum Alloy) using Q Blade software are shown in Fig 6.6 to 6.10. The simulation results show that the maximum Z axis tip deflection generated is 2240.25 mm which is for Aluminum Alloy and the minimum of Z axis deflection generated is 140.79 mm which is for Epoxy carbon. The simulation results also show that the Z axis deflection generated for the selected five materials for the designed geometry varies within the materials to a large extent.

???????D. Stress and Tip Deflection Analysis

The static analysis of composite wind mill blade had been carried out in this section. Comparison between different composite materials like Structural Steel, E-glass, S-glass, Epoxy Carbon, Aluminium Alloy are made under same load condition. Von-Mises Stresses and deformations both in Z and X directions are simulated using QBlade software. The simulation results imply that for all the materials the maximum Von-Mises stress is very close. However, in case of mass Epoxy Carbon shows the least value. Also the Z as well as the X axis tip deflection is the least in case of Epoxy Carbon and the Von-Mises Stress of 502.98 MPa is far below the Maximum Tensile stress of 1632 MPa in case of Epoxy Carbon. It can be concluded that Epoxy carbon is more suitable in making the wind turbine blade.

TABLE VI
stresses and deflection for the designed blade against different materials

Conclusion

Selection of optimal blade profile from six number of NACA 4-digit series Airfoils based on maximum lift to drag ratio is carried out and the Airfoil profile NACA 4406 is selected. Glide ratio for different airfoils are compared for different Reynolds number of flow. Lift coefficient CL = 0.75 and angle of attack ? = 2.50 degree is selected based on the above comparisons. The geometric parameters of the wind turbine i.e. chord lengths and blade twist angles are calculated along the blade span by dividing the blade into 40 equal segments, using Blade Element Momentum (BEM) theory with the help of R programming and then the calculated values are linearized between 50% and 90% of the blade span. Solid structure modeling of the blade is further carried out in QBlade software using both the calculated non-linearized and linearized chord lengths and blade twist angles values. Lift and Drag forces as well as tangential and thrust forces for all the elements along the blade span are calculated. Torque as well as power for each element are also calculated. The total power output of the turbine is found to be 6.96 kW taking the turbo-generator efficiency as 80%. The linearized model is further used in QBlade software , where the calculated values of forces for different elements are simulated for stress analysis of the blades using Von Mises failure theory for different materials like Structural steel, E-Glass, S-glass, Epoxy Carbon and Aluminum Alloy. Tip deflection both in Z as well as in X axis direction are simulated and all the values of stresses and deflections as well as mass are taken into account towards consideration of the design feasibility. Epoxy Carbon is found to be best material for designing the wind turbine blades. The designed blade can be subjected to further analysis like CFD simulation, vibration analysis, variation of power with change in angle of attack, reduction in cut in speed for low Reynolds number flow due to boundary layer separation, dynamic response of the wind turbine blade, fatigue life assessment, composite material analysis for minimizing blade mass subjected to constraints like maximum allowable stress and blade tip deflection and even testing of a model in a wind tunnel.

References

[1] Mahawadiwar H.V. , Dhopte V.D. , Thakare P.S. , Askhedkar R.D. , CFD Analysis of wind turbine blade. International Journal of Engineering Research and Applications (IJERA). 2 , 3188 – 3194 , 2012 . [2] Muiruri P.I. , Motsamai O.S. , Three Dimensional CFD Simulations of a Wind Turbine Blade Section. Journal of Engineering Science and Technology Review. 11, 138-145, 2018 [3] Biadgo A.M. , Aynekulu G. , Aerodynamic Design of Horizontal Axis Wind Turbine Blades. IFME Transactions , Faculty of Mechanical Engineering , Belgrade . 45 , 647- 660 , 2017 [4] Manwell J.F. , McGowan J.G. , Rogers A.L. , Aerodynamics of wind turbine . Wind Energy Explained – Theory, Design and Application. 83-138 , 2002 [5] Fuentes S. , Valentin, Troya, Cesar, Moreno, Gustavo, Molina, Jaime , Airfoil selection methodology for Small Wind Turbines. International Journal of Renewable Energy Research . 6 , 1410-1416 , 2016 [6] Najar F.A. , Harmain G.A. , Blade Design and Performance Analysis of Wind Turbine . International Conference on Global Scenario in Environment and Energy , 5 , 1054-1061 , 2013 [7] Amano R.S. , Malloy R.J. , CFD Analysis on Aerodynamic Design Optimization of Wind Turbine Rotor Blades . World Academy of Science, Engineering and Technology International Journal of Mechanical and Mechatronics Engineering . 3 , 1450-1454 , 2009 [8] Liu X. , Wang L. , Tang X. , Optimized linearization of chord and twist angle profiles for fixed-pitch fixed-speed wind turbine blades. Renewable Energy and International Journal . 57 , 111-119 , 2013 [9] Sarangi S. , Dynamic analysis of wind turbine blade . Bachelor’s Thesis . Department of Mechanical Engineering , National Institute of Technology , Rourkela , 769008 [10] Mishnaevsky L. , Branner K. , Petersen H.N. , Beauson J. , McGugan M. , Sorensen B.F. , Materials for Wind Turbine Blades: An Overview. Technical report , Department of Wind Energy, Technical University of Denmark, 4000 Roskilde, Denmark , November 9 , 2017. [11] Sarkar A. , Behera D.K. , Wind Turbine Blade Efficiency and Power Calculation with Electrical Analogy. International Journal of Scientific Research and Publications . 2 , 2012 [12] Patel N.S. , Patel D.C. , Shah R.A. , Desai N.K. , Nayi K.H. , Design of Horizontal Axis Wind Turbine . International Journal for Scientific Research and Development . 4 , 208-211 , 2016 [13] Cotrell J. , The Mechanical Design, Analysis, and Testing of a Two-Bladed Wind Turbine Hub. Technical Report , Master of Science in Engineering, The University of Texas at Austin, December 1997 [14] Ajoko , John T. , Horizontal Axial Wind Turbine Blade Design Using Ansys Fluent . Journal of Multidisciplinary Engineering Science Studies (JMESS). 2 , 798-803, 2016 [15] Chaudhary U. , Mondal P. , Tripathy P. , Nayakand S.K. , Saha U.K. , Modeling and Optimal Design of Small HAWT Blades for Analyzing the Starting Torque Behavior. IEEE . 3 , 2014 [16] Reddy K.A. , Dagamoori K. , Sruthi A.P. , Naga S.A. , Mahalakshmi N.N. , Krishna Reddy A.V. , Rajesh B. , Kumar K.K. , Shivasri C. , Ali S.Y. , A Brief Research, Study, Design and Analysis on Wind turbine. International Journal of Modern Engineering Research . 5 , 2015. [17] Wetzel K. , Hale R. , Depcik C. , Allen C. , The design report 400W portable wind turbine . Technical report , Department of Aerospace and Mechanical Engineering , The University of Kansa , April 18 , 2013 [18] Mutkule K. , Gorad P.P. , Raut S.R. , Optimum and Reliable Material for Wind Turbine Blade. International Research Journal of Engineering and Technology . 4, 2014 [19] Kale S. , Hugar J. , Static Strength Design Of Small Wind Turbine Blade Using Finite Element Analysis And Testing . ASME International Mechanical Engineering Congress and Exposition , Houston , Texas , USA . 4B ,13-19 , 2015 [20] Rashedi A. , Sridhar I. , Tseng K.J. , Multi-objective material selection for wind turbine blade and tower. Elsevier , Materials and Design . 37 , 521-532 , 2012 [21] Perkins F.W, Cromack Duane E . Wind Turbine Blade Stress Analysis and Natural Frequencies. Technical report , Energy Alternatives program , University of Massachussets , Amherst , Massachussets , 01003 , August 1978 [22] Ingram G. , Wind Turbine Blade Analysis using the Blade Element Momentum Method .Version 1.1 , Durham University , October 18 , 2011 [23] Rehman S. , Alam M.M. , Alhems L.M. , Rafique M.M. , Horizontal Axis Wind Turbine Blade Design Methodologies for Efficiency Enhancement. Energies(19961073). 11 , 506-539 , 2018

Copyright

Copyright © 2023 Aritra Kumar Das. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.