Stochastic Reliability Modelling of Hr/M/1/N Queueing System with Working and Working-Breakdown States

Abstract

This study models the reliability, availability, and maintainability of a finite capacity Hr/M/1/N phase queueing system in working and working-breakdown states. The arrival times are distributed according to a Hyperexponential distribution with r-parallel phases, whereas the service times are distributed according to an exponential distribution. The differential-difference equations for the transient states are derived from the state-transition diagram for different environmental states, as well as failure and recovery states. For the particular situation of N=4, these governing equations are solved numerically. Sensitivity Analysis was used to investigate RAM performance measures for various parametric variables.

Introduction

I. INTRODUCTION

The study of a series of service stations through which each arriving customer must proceed before leaving the system is one of the most common applications of queueing theory. When the output from one service station becomes the input to the next, i.e., when units departing from one station are not collected and then moved on to the next station in a batch, the analysis of the system's behaviour requires the determination of the inter-departure time distribution at each stage, which is then used as the inter-arrival time distribution to the next station. This tends to be the most challenging component of the analysis in general. Therefore, for such queueing model the arrival or service times can be modelled with Phase type distributions and these models are used to measure the characteristics of queueing system. In such models, finding an ideal solution is very difficult and these models usually consider better approximations. As a result, a new technique to the study of G/M/1 systems with phase type distributions appears to be promising. One of the input distribution G can be assumed to be the blend of two exponential probability distributions, i.e., Hyperexponential distribution Hr. In this context, queuing system with Hyperexponential input distributions is more complex system as compared to Exponential or Erlang distributions and it is challenging to find an analytical solution. A Hyperexponential distribution is a continuous probability distribution which consists of two or more non-identical phases that occur in a exhaustive or parallel manner.

Cosmetatos and Godsave (1986), have developed hyper-exponential Hr/M/1 inter-arrival and exponential service times queueing model with multi-server system. They developed an approximate formula for the equilibrium queue-size and queueing-time distributions. These formulas are based on the combination of heuristic arguments, analytical methods and the model is also dealt with the sensitivity analysis. Tian et al. (1989), examined the G1/M/1 queue with exhaustive service and multiple exponential vacations. The authors represent the embed Markov chain's transition matrix as a block-Jacobi form and provided a matrix-geometric solution. In addition, the limiting behaviour of continuous time queue length processes, probability distributions for the waiting times and the busy period were also explored. Tarasov et al. (2019) studied the H2/M/1 queueing system and determined the mean delay time for different approaches and compared. Furthermore, the authors were able to optimise the constraints to find the characteristics for the H2/M/1 queueing system. Reliability theory is a well-developed field and has been researched by several authors. The computation of the Reliability of a system with parts showing dependent failures and repairs for any system is in general complex, and several methods are proposed which are available in the literature. Amiri et al. (2007) presented a methodology for assessing system transient survivability and availability in the presence of identical components and repairmen. To create the technique for the transient reliability of such systems, the authors used the ideas of Markov models, eigen vectors, and eigenvalues. The suggested approach is a more effective method and can be used to analyse a wide range of systems, including series, parallel, and k-out-of-n systems.

The proposed approach may also be used to calculate MTTFs and the time required for the system to attain steady state. There hasn't been much work done on the RAM analysis of the Hr/M/1 queueing system with working and working-breakdown states. As a result, this inspires to study the reliability, availability and maintainability analysis for hyper exponential single server finite capacity queuing system with working, working-breakdowns, failure and recovery policies.

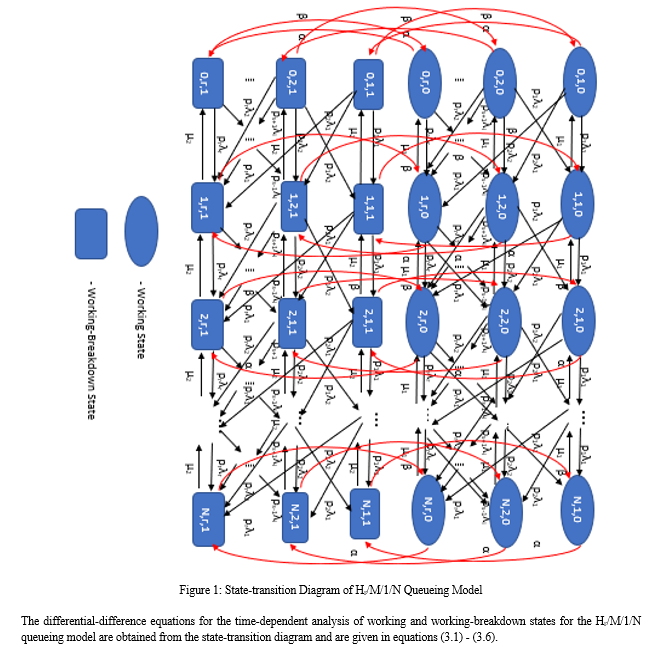
In this chapter the RAM analysis of the Hr/M/1/N queueing model with two different environmental states is analysed. The arrival process is modelled by Hyperexponential random variable with r phases of arrival with rate λr. The unit is arrived only by one phase of arrival that is chosen according to a discrete distribution pi, i=1rpi=1 . This Hyperexponential distribution has rate λ1 with probability p1 and rate λ2 with probability p2and so on. Let S(t) denote the environmental states such as the working and working breakdown states at time t. When the system is in the working state failure occurs in the queueing system with the failure rate α. The system is immediately switched to the working-breakdown state where the recovery process takes place with the recovery rate β. During this process, the system did not terminate its function but it continues its process at a slow pace. The differential-difference equations are formed from the state-transition diagram for the Hr/M/1/N queueing model and this model is numerically illustrated for the special case. The Fourth-Order Runge-Kutta numerical method is used to solve the transient probabilities for the Hr/M/1/N queueing model. The Reliability, Availability and Maintainability of the Hr/M/1/N queueing are analysed numerically and presented graphically. The sensitivity analysis was also performed to study the system change for changes in the model parameters.

II. PRESUMPTIONS AND NOTATIONS

The presumptions that are used in this chapter are:

1. The arrival of units to the system are assumed to follow Hyperexponential distribution with r phases.
2. The service process is exponentially distributed with FCFS (First Come First Serve) queue discipline
3. When the system is not empty (i.e., at least one unit must be present), a failure rate arises with exponential rate α. The system immediately changes to Working-Breakdown mode, where it runs at a reduced rate.
4. The recovery process occurs in the system's working-breakdown, which is exponentially distributed. When the system recovers, it returns to its normal working state of operation
5. All arrival and the service times are independent of each other

The following are the notations that are used in this chapter:

RAM      :              Reliability, Availability and Maintainability 

N(t)        :              Total number of machines in the system at any time t

Hr           :              Hyper exponential distribution with r identical parallel phases

S(t)         :              The environmental state at any instant of time t                                                                                                                                                                                                                                                                                                                                                                                                                                                                                               

R(t)        :              Reliability of the system at time t

A(t)        :              Availability of the system at time t

M(t)       :              Maintainability of the system at time t

λr            :              Arrival rate for the rth phase

µ1               :                  Service rate for working state

µ2               :                  Service rate for working-breakdown state (µ1 > µ2).

α                 :                  Failure rate

β                 :                  Recovery rate

Pn, i, j(t)   :              Probability that there are n machines in the system with ith phases and jth states at time t

Pn(t)       :              Probability that there are n units in the system at time t

Pw(t)       :              Probability of n units in the system for the working state at time     t

Pwb(t)     :              Probability of n units in the system for the working-breakdown State at time t

pk               :                   Probability that the arrival choosing kth phase

II. RAM MODELLING OF Hr/M/1 QUEUEING SYSTEM

In this section the analysis of the Reliability, Availability, and Maintainability for Hr/M/1/N queueing system with two different environmental states are analysed.  In Hr/M/1/N queueing systems, the arrival process is modelled by the Hyperexponential random variable with r phases of arrival with rates λr. In this case, the arrival phases should be of parallel structure, i.e., a unit arrive only to one phase, each is chosen according to a discrete distribution pk, k=1rpk=1 .

The arrival process is according to hyperexponential distribution has rate λ1 with probability p1, rate λ2 with probability p2and so on. The service process is exponentially distributed with two parameters µ1 and µ2 depending on the environmental states such as working and working-breakdown.  The failure occurs in the working state of the system with failure rate α, the system immediately moved its process to the working-breakdown state where the recovery process takes place with recovery rate β. Once the recovery occurs the state of the system is transposed to the working state. The failure and the recovery rates are exponentially distributed. Figure 1 exhibits the state-transition diagram for Hr/M/1/N queueing model.

Conclusion

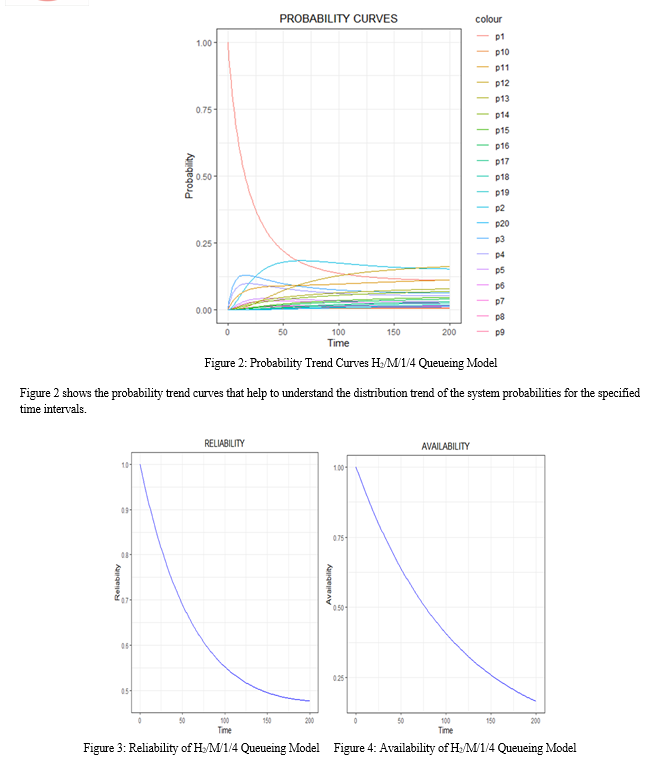
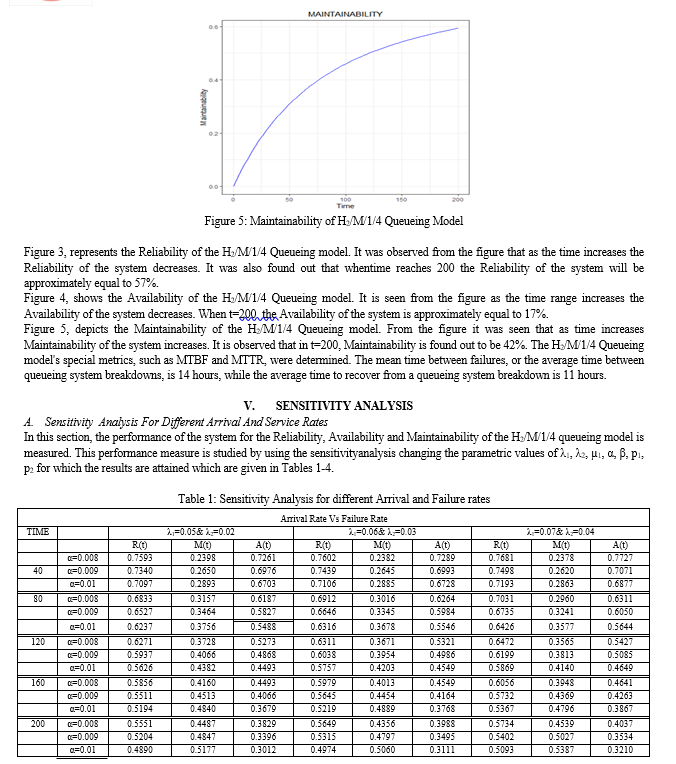
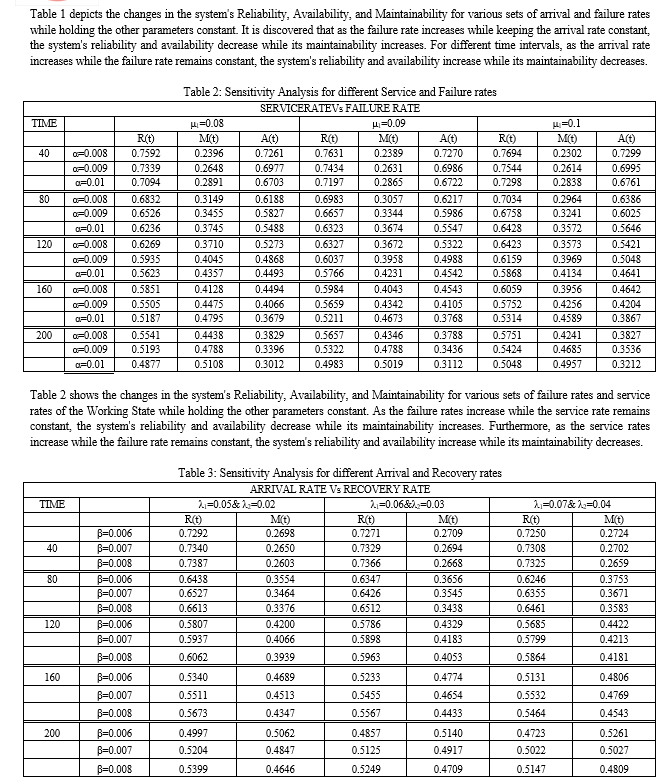
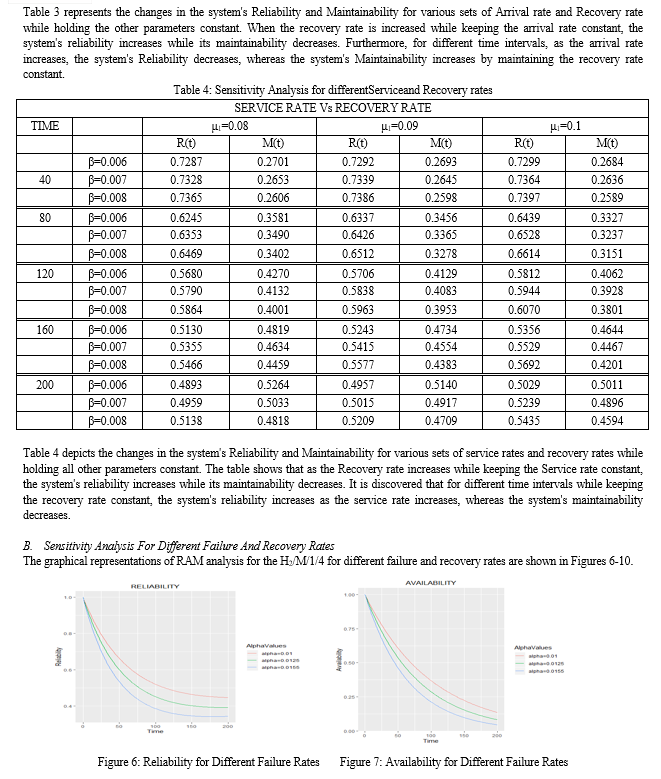
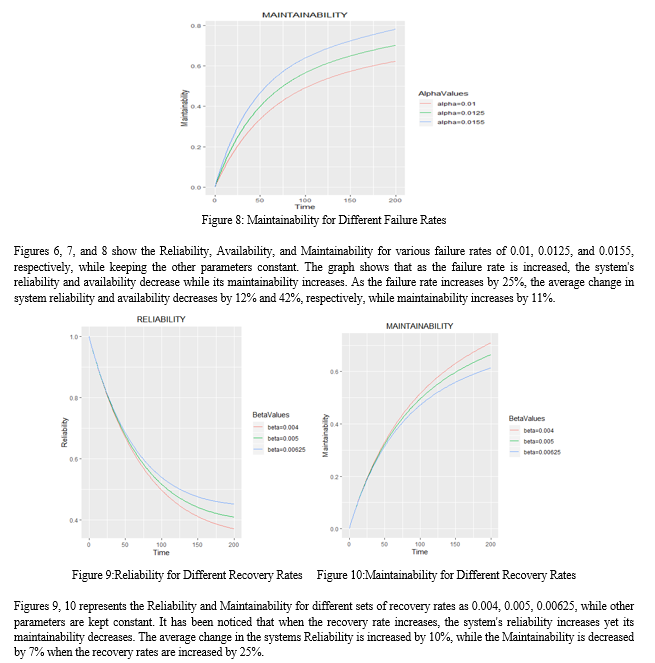
The RAM analysis of the Hr/M/1/N Queueing model with two different environmental conditions is examined in this chapter. The state-transition diagram is used to obtain the differential-difference equations for the transient state of the r-phase Hyperexponential queueing model. Hyperexponential 2-phase inter-arrival times and exponential service times are assessed for a single server system with finite capacity as a specific case. The differential-difference equations for the H2/M/1/4 queueing model with working and working-breakdown states are solved using the fourth order Runge-Kutta numerical method. The following are the outcomes: 1) It was discovered that as time passes, the reliability and availability of the system decreases, while the maintainability of the system increases. 2) When t=200, the system\'s Reliability and Availability were found to be 57 percent and 17 percent, respectively, whilst the system\'s Maintainability was determined to be 42 percent. 3) The average time between queueing system failures, or mean time between failures, is 14 hours, whereas the average time to recover from a queueing system failure is 11 hours. 4) For a fixed Failure rate, the Sensitivity Analysis was used to examine various sets of Arrival and Service rates. The H2/M/1/4 Queueing model increases the system\'s reliability and availability while decreasing its maintainability. 5) For a fixed recovery rate, the system\'s Reliability decreases as the arrival rates increase, while the system\'s Maintainability increases, and for a growing service rate, the system\'s Reliability increases while the Maintainability decreases. 6) When the failure rates increase by 25%, the average change in system reliability and availability decreases by 12% and 42%, respectively, while the system\'s maintainability increases by 11%. 7) It has been discovered that for every 25% increase in recovery rate, the average change in system reliability increases by 10%, while system maintainability decreases by 7%.

References

[1] Al Hanbali, A. (2011). Busy period analysis of the level dependent PH/PH/1/K queue. Queueing Systems, 67(3), 221–249. doi:10.1007/s11134-011-9213-6 [2] Amiri, M., & Ghassemi-Tari, F. (2007). A methodology for analyzing the transient availability and survivability of a system with repairable components. Applied Mathematics and Computation, 184(2), 300–307. doi:10.1016/j.amc.2006.05.177 [3] Baba, Y. (2005). Analysis of a GI/M/1 queue with multiple working vacations. Operations Research Letters, 33(2), 201–209. doi:10.1016/j.orl.2004.05.006 [4] Balagurusamy .E (2003), “Reliability Engineering”, Tata McGraw-Hill Publishing Company Limited, New Delhi [5] Chakravarthy, S. R., Shruti, & Kulshrestha, R. (2019). A queueing model with server breakdowns, repairs, vacations, and backup server. Operations Research Perspectives, 100131. doi:10.1016/j.orp.2019.100131 [6] Cosmetatos, G. P., & Godsave, S. A. (1980). Approximations in the Multi-Server Queue with Hyper-Exponential Inter-Arrival Times and Exponential Service Times. The Journal of the Operational Research Society, 31(1), 57. doi:10.2307/3009336 [7] Jiang, T., & Liu, L. (2015). The GI/M/1 queue in a multi-phase service environment with disasters and working breakdowns. International Journal of Computer Mathematics, 94(4), 707–726. doi:10.1080/00207160.2015.1128531 [8] Jinting, W. (2006). Reliability analysis M/G/1 queues with general retrial times and server breakdowns*. Progress in Natural Science, 16(5), 464–473. doi:10.1080/10020070612330021 [9] Liu, X., & Fralix, B. (2018). On Lattice Path Counting and the Random Product Representation, with Applications to the Er/M/1 Queue and the M/Er/1 Queue. Methodology and Computing in Applied Probability. doi:10.1007/s11009-018-9658-8 [10] Marin, A., & Rota Bulò, S. (2014). Explicit solutions for queues with Hypo- or Hyper-exponential service time distribution and application to product-form approximations. Performance Evaluation, 81, 1–19. doi:10.1016/j.peva.2014.07.021 [11] Ren, Q., & Kobayashi, H. (1995). Transient solutions for the buffer behaviour in statistical multiplexing. Performance Evaluation, 23(1), 65–87. doi:10.1016/0166-5316(93)e0064-c [12] Shyamala, S., & Vijayaraj, R. (2020). Time dependent solution of two stages M[X]/G/1 queue model server vacation random setup time and balking with Bernoulli schedule. PROCEEDINGS OF INTERNATIONAL CONFERENCE ON ADVANCES IN MATERIALS RESEARCH (ICAMR - 2019). doi:10.1063/5.0017027 [13] Tarasov. V. (2018), “Research of dual systems H2/M/1 and M/H2/1 with exponential and hyperexponential input distributions”, International Scientific-Practical Conference: Problems of Info-communications Science and Technology (PIC S&T), IEEE, 793–796 [14] Tian, N., Zhang, D. & Cao, C. The GI/M/1 queue with exponential vacations. Queueing Syst 5, 331–344 (1989). https://doi.org/10.1007/BF01225323

Copyright

Copyright © 2023 S. R. Sruthi, Dr. P.R. Jayashree. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.